一文多图讲清楚解决最长回文子串问题的【中心扩展算法】与【Manacher算法】

零、引入

首先来看一道题目：

给定一个字符串 s，找出 s 中的最长回文子字符串。1 <= s.length <= 1000。

例如，给定字符串 str = "abbacdefedc"，该字符串中的回文子字符串有 "abba"、"bb"、"cdefedc"、"defed"、"efe"，单个字符也是回文字符串，这里没有列举，在所有的回文子字符串中最长的是 "cdefedc"。

先看题目

这道题目意思很明确，找出所有回文子字符串中最长的那一个。

再看数据

数据量达到 $10^3$，于是暴力枚举子字符串始末位置再判断子串是否回文的方法就不要尝试了，必然过不了的，因为【暴力法】的时间复杂度为 $O(n^3)$。接下来我们将介绍一个时间复杂度为 $O(n^2)$ 的方法以及一个时间复杂度上最优的方法，也是今天的主角——【Manacher算法】。

一、中心扩展算法

中心扩展算法是解决回文子串问题的一种重要的算法，是后面要讲的【Manacher算法】的重要基础。

1.1 算法思想

在介绍中心扩展算法之前，需要先了解一下回文中心、奇数回文字符串以及偶数回文字符串的概念。

回文字符串的回文中心指的是字符串的中心位置，回文中心可以是一个字符也可以是两个字符。以单个字符为回文中心的回文字符串长度为奇数，故奇数回文字符串因此得名。而以两个字符为回文中心的字符串长度为偶数，于是被称为偶数回文字符串。

中心扩展算法，是从回文中心向两侧扩展的一种算法。具体来说，以某一个字符为中心或者与下一个字符构成中心向两侧扩展，并判断扩展的字符串与中心字符串构成的子串是否是回文子串，直到子串不再是回文子串或到达字符边界才停止扩展，该方法需要枚举所有可能的回文中心，并在扩展过程中记录最长的回文子串。

1.2 图解

回文中心可能是一个字符也可能是两个字符，接下来将通过图示的方式来进行介绍。

首先来看，回文中心是一个字符的情况。

（1）图解例子中，字符串s="abcbac"，我们以字符'c'作为回文中心为例。

（2）left和rigth指针指向向外扩的字符下标，因为s[left]=s[right]，所以字符串"bcb"是一个回文子串，接下来继续向外扩。

（3）left和rigth指针指向了新的向外扩的字符下标，因为s[left]=s[right]，所以字符串"abcba"是一个回文子串，接下来继续向外扩。

（4）left指针超出了字符串s的左边界，因此扩展停止，最终获得的最长回文子串为s[left+1,...right-1]="abcba"。

现在看一下回文中心是两个字符的情况。

（1）字符串s="abccbc"，现在以字符串cc作为回文中心向两侧扩展。

（2）left和rigth指针指向的是向外扩的字符下标，因为s[left]=s[right]，所以字符串"bccb"是一个回文子串，接下来继续向外扩。

（3）left和rigth指针指向了新的向外扩的字符下标，因为s[left]!=s[right]，因此扩展停止，最终获得的最长回文子串为s[left+1,...right-1]="bccb"。

1.3 示例代码

解决该题的中心扩展算法代码如下所示：

// 扩展算法
pair<int, int> expandAroundCenter(const string& s, int left, int right) {
	while (left >= 0 && right < s.size() && s[left] == s[right]) {
		--left;
		++right;
	}
	return {left+1, right-1};
}

// 求最长回文子串
string longestPalindrome(string s) {

    int start = 0, end = 0;
    for (int i = 0; i < s.size(); ++i) {
        auto [left1, right1] = expandAroundCenter(s, i, i);
        auto [left2, right2] = expandAroundCenter(s, i, i+1);
        
        if (right1 - left1 > end - start) {
            start = left1;
            end = right1;
        }
        if (right2 - left2 > end - start) {
            start = left2;
            end = right2;
        }
    }
    
    return s.substr(start, end - start + 1);
}

1.4 复杂度分析

时间复杂度：$O(n^2)$，其中 $n$ 是字符串的长度。长度为 $1$ 和 $2$ 的回文中心分别有 $n$ 和 $n-1$ 个，每个回文中心最多会向外扩展 $n$ 次。

空间复杂度：$O(1)$ 。

二、Manacher 算法

对于最长回文子字符串的问题，我们用了一个时间复杂度为 $O(n^2)$ 的中心扩展算法来解决，这种算法在时间复杂度上已经相对较优了，但是还有一种线性时间复杂度的算法——【Manacher 算法】。

【Manacher 算法】由 Glenn Manacher 于1975年发明。

该算法是用来解决 最长回文子串 的问题，但是算法中的 最长回文半径 思想可以来解决其他类似的问题。

2.1 字符串预处理

在中心扩展算法中，我们已经知道回文字符串根据长度可以分为奇回文串和偶回文串，现在可以通过给原字符串增加特殊字符的方式将这两种情况统一起来。比如，在相邻两个字符之间、字符串的首字符前和尾字符后分别增加一个特殊字符# 。增加了#字符之后，字符串s="bcba"将变为str="#b#c#b#a#"。此时，无论是奇回文串还是偶回文串，我们都可以按照回文中心为一个字符的情况向字符两侧扩出去找到最大回。

增加的这一个特殊字符有没有什么要求，比如不能是原来字符串中出现过的字符呢？不需要！因为就算这个特殊字符在原字符串中出现出现过，不会影响最终的结果，因为增加的特殊字符只会和特殊字符本身进行回文判断，不会和原有字符串进行字符比较。现在通过图示简单解释一下：

现在有一个字符串"abba"，分别增加字符'#'和'a'进行预处理操作，但是我们可以发现在这两种操作中，新字符的最长回文子串的长度是一样的，说明增加哪一种字符对计算最长回文子串长度没有影响。

2.2 算法思想

Manacher 算法的基本思路依旧是遍历每一个字符，以当前字符为中心向左右两侧进行回文扩展。相对于朴素的中心扩展算法，该算法将遍历前面字符计算得到的回文串的信息记录下来，以方便遍历后面字符串时计算回文串。遍历过程中被记录下来的几个信息包括字符串的 回文半径数组、回文右边界 以及 回文中心坐标。在分析该算法的几种情况之前需要先将几个概念梳理一下。

2.2.1 重要概念

• 最大回文半径、直径：最大回文直径指的是以某一个字符为回文中心向左和右两边扩展得到的最大回文字符串的长度。最大回文半径则指的是以某一个字符为回文中心向左边或者右边一侧扩展得到的最大回文字符串长度。对于 str = "#c#a#b#a#c#" 这样一个回文字符串，以字符 $b$ 为中心的最大回文直径为 11，回文半径为 6。

• 最大回文半径数组 $pArr$：该数组的长度与预处理后新的字符串 $str$ 长度一样。$pArr$ 是用来记录最大回文半径的数组。对于字符串str="#c#a#b#a#c#"来说 ，$pArr[\mathrm{0...10}]=[1,2,1,2,1,6,1,2,1,2,1]$。

• 整数 R：这个变量的意义是之前遍历的所有字符的所有回文半径中，最右即将到达的位置，$R-1$ 是目前可以到达的最远位置。$R$ 初始设置为 -1。还是以str="#c#a#b#a#c#"来说明：

  str[0]='#' 的回文半径为 1，所以目前回文半径向右只能扩到位置 0，回文半径最右即将到达的位置 $R=1$；

  str[1]='c' 的回文半径为 2，所以目前回文半径向右只能扩到位置 2，回文半径最右即将到达的位置 $R=3$；

  str[2]='#' 的回文半径为 1，所以目前回文半径向右只能扩到位置 2，回文半径最右即将到达的位置不变，仍是 $R=3$；

  str[3]='a' 的回文半径为 2，所以目前回文半径向右只能扩到位置 4，回文半径最右即将到达的位置 $R=5$；

  str[4]='#' 的回文半径为 1，所以目前回文半径向右只能扩到位置 4，回文半径最右即将到达的位置不变，仍是 $R=5$；

  str[5]='b' 的回文半径为 6，所以目前回文半径向右只能扩到位置 10，回文半径最右即将到达的位置 $R=11$；

  此时已经到达了字符数组的结尾，所以之后过程中的 $R$ 值不会再有变化了。$R=11$ 就是遍历过的所有字符中向右扩出来的最大右边界（取不到）。

• 整数 C：表示最近一次更新 $R$ 时的回文中心坐标。拿刚刚的例子来说，遍历到 str[0] 时 $R$ 更新，于是$C=0$；遍历到 str[1] 时，$C=1$；…遍历到 str[5] 时 $R$ 更新，$C=5$。在之后的过程中，$R$ 不再更新，于是 $C$ 一直是 5。

2.2.2 几种情况

我们的目标是找出原字符串 s 的最大回文子串，那么只要找出预处理后的字符串 str 的最长的回文半径 r 。我们在更新 $pArr$ 数组的过程中，就能找出最大回文半径，记录此时的最长回文子串的始末位置 $start$ 和 $end$，最后在输出 str 中位于始末位置之间的非特殊字符的字符串记为最终答案。

重点就在于更新 $pArr$ 数组。

现在我们从左到右依次计算 $pArr$ 数组中每个位置的值，在字符串 str 的位置 i 处，将会有以下几种情况出现：

情况一：$R-1$ 位置没有包住当前 i 的位置。

比如 "#c#a#b#a#c#"，计算到 str[1]='c' 时，$R=1$。1 位置为最右回文右边界即将到达的位置，实际的最右回文右边界位置在 $R-1=0$ 处，此时 $R-1$ 位置没有将当前的 $i$ 位置包住。这个时候没有任何的加速操作，只能使用朴素的【中心扩展算法】从 $i$ 位置字符开始，向左右两侧扩展找出最长回文半径。情况一如下图所示。

情况二：$R-1$ 位置包住了当前 i 的位置，包括 $R-1=i$ 的情况。该情况可以翻译为 $R-1>=i$ 等价于 $R>i$。

比如 "#c#a#b#a#c#"，我们在计算 $pArr[5]$ 时更新 $R=11$，在计算 $pArr[\mathrm{6...10}]$ 时，仍然是 $R=11$，此时的 $R-1=10$ 包住了位置 6...11。在这种情况下，我们可以利用数组 $pArr$、整数 $R$ 以及整数 $C$ 来加速计算，这也是 Manacher 算法的核心，铺垫了这么多终于要讲到核心内容了😂😂😂。

当前遍历到位置 $i$ 是位于回文中心 $C$ 和最右回文右边界 $R-1$ 之间的某个位置的，因为 $R-1$ 位置包住了当前 i 的位置，一定是在前面某个位置 j 处，$R-1$ 和 $C$ 更新了。情况二如下图所示。

既然回文半径数组 $pArr$ 是从左到右计算的，所以位置 i 之前的所有位置都已经计算过回文半径。假设位置 i 以 $C$ 为中心向左对称过去的位置为 $i^{{}^{\prime }}$，那么位置 $i^{{}^{\prime }}$ 的回文半径也是计算过的。此时，以 $i^{{}^{\prime }}$ 为中心的最大回文子串必然只有三种情况，接下来将依次进行分析，假设以 $i^{{}^{\prime }}$ 位置为中心的最长回文字符串的左边界和右边界分别记为 $l$ 和 $r$，$R-1$ 关于 $C$ 的对称位置记为 $L$。

情况 2-1

以 $i^{{}^{\prime }}$ 位置为中心的最长回文字符串的 $l$ 和 $r$ 完全位于边界 $L$ 与 $R-1$ 之内，此时以 $i$ 位置为中心的最长回文字符串等同于以 $i^{{}^{\prime }}$ 位置为中心的最长回文字符串。情况 2-1 如下图所示。

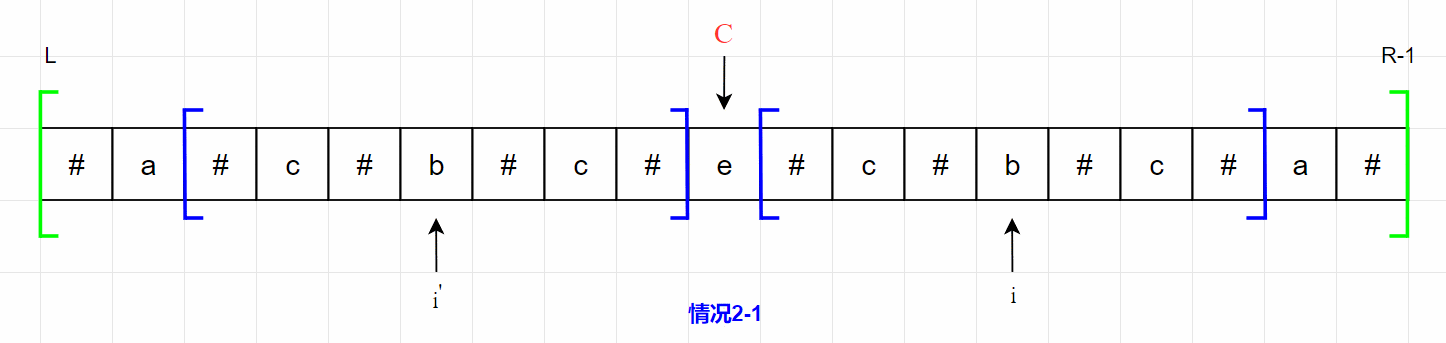
为什么以 $i$ 位置为中心的最长回文字符串等同于以 $i^{{}^{\prime }}$ 位置为中心的最长回文字符串？

我们现在来证明一下，记 $i^{{}^{\prime }}$ 位置回文左边界左侧的第一个字符为 $X$ ，回文右边界右侧的第一个字符为 $Y$，记 $i$ 位置回文左边界左侧的第一个字符为 $Z$ ，回文右边界右侧的第一个字符为 $K$ 。

如果 $Z!=K$ ，则可以说明此时以 $i$ 位置为中心的最长回文字符串等同于以 $i^{{}^{\prime }}$ 位置为中心的最长回文字符串。

因为 $X$ 和 $Y$ 位于以位置 $i^{{}^{\prime }}$ 为中心向两侧扩展的外侧，所以 $X!=Y$ 。因 $X$ 和 $K、Y$ 和 $Z$ 都关于回文中心 $C$ 对称，所以 $X=Z、K=Y$ 。联合 $X!=Y$ 于是 $Z!=K$，原命题得证。

情况 2-2

以 $i^{{}^{\prime }}$ 位置为中心的最长回文字符串超出了边界 $L$，此时以 $i$ 位置为中心的最长回文字符串是 $L$ 到 $L^{{}^{\prime }}$ 区域，也是 ${(R-1)}^{{}^{\prime }}$ 到 $R-1$ 的区域。其中 $L^{\prime }$ 是 $L$ 关于 $i^{\prime }$ 右侧对称位置，${(R-1)}^{{}^{\prime }}$ 是 $R-1$ 关于 $i$ 的左侧对称位置。情况 2-2 以及一些标记、如下图所示。

现在记 $L$ 左侧的第一个字符为 $X$，$L^{\prime }$ 右侧的第一个字符为 $Y$，$(R-1{)}^{\prime }$ 左侧的第一个字符为 $Z$，$R-1$ 右侧的第一个字符为 $K$。按照 情况 2-1 中类似推导有，$X==Y、Y==Z、X!=K$ ，于是有 $Z!=K$，所以此时以 $i$ 位置为中心的最长回文字符串为 $L$ 到 $L^{\prime }$ 区域。

情况 2-3

压线的情况，即以 $i^{{}^{\prime }}$ 位置为中心的最长回文字符串的左边界与 $L$ 重合的情况，这个时候以 $i$ 位置为中心的最长回文字符串的长度至少是以 $i^{{}^{\prime }}$ 位置为中心的最长回文字符串，并且还要继续对以 $i$ 位置为中心的字符串进行扩展。情况 2-3 如下图所示。

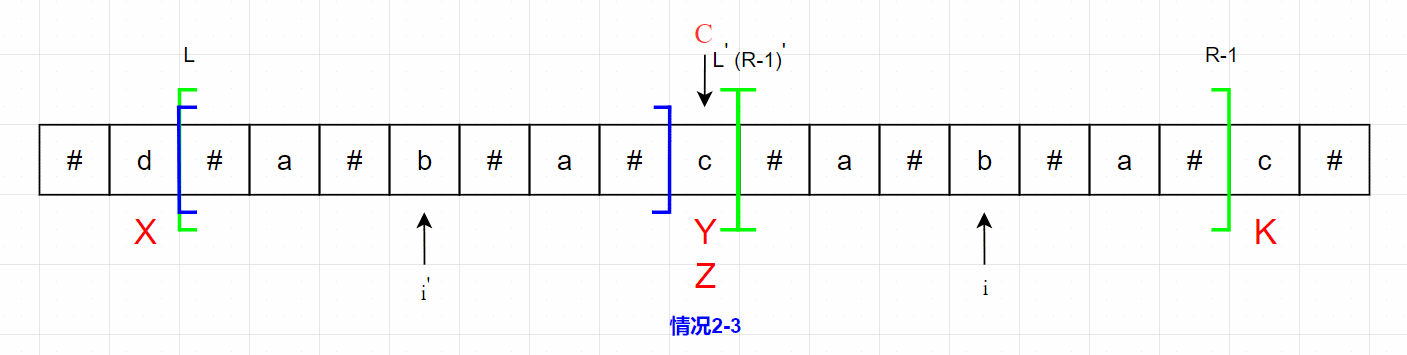
在该情况中，$X!=Y、Y==Z、X!=K$ ，此时无法判断 $K$ 与 $Z$ 的关系，所以还要继续对以 $i$ 位置为中心的字符串进行扩展才能得到正确答案。

2.3 示例代码

以上分析的几种情况的伪代码如下所示。

/----------------------------伪代码----------------------------/ 
int manacher(string str) {
    // str 是预处理后的字符串
    int n = str.size();
    vector<int> pArr(n, -1);
    int R = -1;
    int C = -1;
    
    for (int i = 0; i < n; ++i) {
        if (情况一) {
            从i往两侧暴力扩展，并且更新 R 和 C
        }
        else {	// 情况二
            if (情况 2-1) {
                pArr[i] = 某个 O(1) 的表达式
            }
            else if (情况 2-2) {
                pArr[i] = 某个 O(1) 的表达式
            }
            else { // 情况 2-3
                只需要从L-R区域的R右侧字符开始往外扩，并确定 pArr 的答案
                还会有 R 和 C 的更新
            }
        }
    }
    返回最大的 pArr[i] - 1
}
/----------------------------以上是伪代码部分----------------------------/

整合 2.2.2 中的几种情况，我们可以对上述伪代码进行优化。

在遍历到 i 位置时，我们对 pArr[i] 进行这样的初始化。pArr[i] = R > i ? min(pArr[2*C - i], R - i) : 1;。

我们来仔细分析一下，这是一个三目运算表达式，R > i 时执行的是 pArr[i] = min(pArr[2*C - i], R - i) ，R <= i 时执行的是 pArr[i] = 1。

R > i 对应的是 ”情况二：$R-1$ 位置包住了当前 i 的位置“，该情况又对应三种情况，pArr[2*C - i] 对应的是 “完全包含” 的情况（情况2-1），于是有 pArr[i] = pArr[i'] = pArr[2*C - i]；R-i 对应的是 “部份包含” 和 “压线” 的情况（情况2-2和情况2-3），此时 pArr[i] 最少为 i 至 R-1 的长度即 R-1-i+1=R-1。

R <= i 对应的是 “情况一：$R-1$ 位置没有包住当前 i 的位置”，此时需要朴素的【中心扩展】，因此直接赋值为 1。

完成 pArr[i] 初始化，我们要进行判断并进行中心扩展，因为对 pArr[i] 的初始化操作是一种通用处理，其他有需要扩展的情况需要继续向外扩，比如情况 2-3 中就需要继续向外扩。

优化后的实现代码如下所示：

string toManacherStr(string s) {
    int n = s.size();
    string res = "";
    for (int i = 0; i < n; ++i) {
        res += '#';
        res += s[i];
    }
    res += '#';
    return res;
}

string longestPalindrome(string s) {
    string str = toManacherStr(s);
    cout << "str: " << str << endl;
    int n = str.size();
    vector<int> pArr(n, -1);
    int R = -1, C = -1;

    int maxLen = INT_MIN, idx;  // maxLen 表示最大回文半径，idx 表示取到 maxLen 时的值
    for(int i = 0; i < n; ++i) {
        pArr[i] = R > i ? min(pArr[2*C - i], R - i) : 1;

        while (i + pArr[i] < n && i - pArr[i] >= 0) {
            if (str[i + pArr[i]] == str[i - pArr[i]]) {
                pArr[i] ++;
            }
            else break;
        }
        
        if (i + pArr[i] > R) {
            R = i + pArr[i];
            C = i;
        }

        if (pArr[i] > maxLen) {
            maxLen = pArr[i];
            idx = i;
        }
    }
    
    maxLen -= 1;
    string res = "";
    for (int i = idx - maxLen; i <= idx + maxLen; ++i) {
        if (str[i] != '#') {
            res += str[i];
        }
    }
    return res;
}

2.4 复杂度分析

时间复杂度：$O(n)$，其中 $n$ 是字符串的长度。对于每个位置 i，扩展要么从当前的回文右边界开始，要么只会进行一步，因此时间复杂度为 $O(n)$。

空间复杂度：$O(n)$ ，因为需要记录回文半径。

三、总结

本篇博文介绍了处理最长回文子字符串问题的【中心扩展算法】和【Manacher 算法】。

中心扩展算法的时间复杂度为 $O(n^2)$，该算法主要思想是遍历每一个回文中心，并向两侧进行回文扩展，需要注意的是回文中心可以是一个字符也可以是两个字符组成的字符串。

Manacher 算法核心思想是利用前面位置计算过的回文半径来更新后面位置的回文半径，时间复杂度为 $O(n)$。需要理解 $R$ 与 $C$ 的含义以及更新时机。

Manacher 算法可以计算最长回文子字符串的长度，也可以找出最长回文子字符串。

以上部分内容参考的是左程云所著的《程序员代码面试指南》主要还是自己对于 Manacher 算法的一些理解。如有任何疑问，可在评论区沟通。

如果有小伙伴需要原书电子资源，可以评论区留下邮箱地址。

写在最后

以上就是本篇文章的内容了，感谢您的阅读。🍗🍗🍗

如果感到有所收获的话可以给博主点一个 👍 哦。

如果文章内容有任何错误或者您对文章有任何疑问，欢迎私信博主或者在评论区指出。💬💬💬