Acwing 1214. 波动数列

最新推荐文章于 2024-03-03 18:15:29 发布

原创最新推荐文章于 2024-03-03 18:15:29 发布 · 427 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #开发语言

思维同时被 2 个专栏收录

94 篇文章

订阅专栏

38 篇文章

订阅专栏

文章介绍了一种使用动态规划解决序列和模运算问题的方法。通过设立状态转移方程，计算在添加a或-b后的序列和取模结果，最终得出满足条件的方案数量。代码示例使用C++实现。

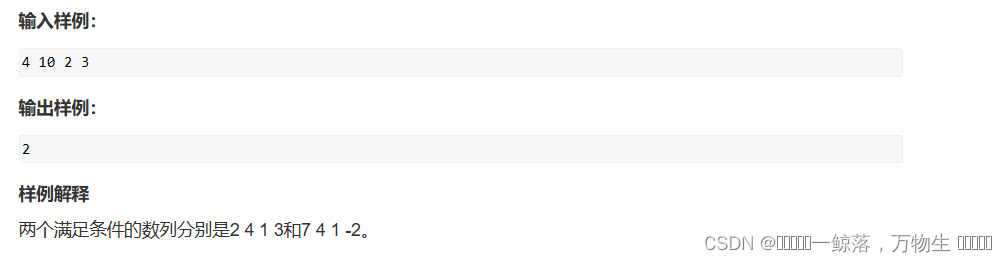
解题思路：首先我们先将式子写一下，我们设第一项为x，di为每次加的数字（a或-b），所以等式如下

$x +( x+d1) + (x+d1+d2 )+...+( x+d1+d2+...+dn-1) =s$

整理后可得

$nx+(n-1)*d1+(n-2)*d2+...+dn-1 = s$

因为第一项x是一个变化范围很大的数字，所以我们先不管它，先去看后面的d，我们再次变形可得

$x=\frac{s-((n-1)*d1+(n-2)*d2+...+dn-1)}{n}$

通过这个式子我们不难发现，只要我们能确定了序列d，那么其对应的首项也就确定了，并且因为x是一个整数，所以分子上的数字必须能整除n。

我们设dp[i][j]表示在第i次选择要加的数（a或-b）后，所选择数字的总和取模n等于j的方案的数量。

状态转移如下：

1、如果第i次我们选择加a，那么通过上述公式我们可以知道，对于第i次的选择di，它最终在总和中一共是加了n-i次，所以此时应该从dp[i-1][((j-(n-i)*a)%n+n)%n]转移得到

2、同理，如果选择减b，就应该从dp[i-1][((j+(n-i)*b)%n+n)%n]转移得到

最后dp[n-1][(s%n+n)%n]就是答案了，因为只有当所有的d加起来的总和%n=s%n时才能整除n。

上代码：

#include <bits/stdc++.h>
using namespace std;
const int mod=100000007;
const int N=1010;
long long n,s,a,b,dp[N][N];
int main()
{
    cin>>n>>s>>a>>b;
    dp[0][0]=1;//dp[i][j]表示第i次选择选a或b，取模n等于j的方案的数量
    for(int i=1;i<n;i++)//第一个数字是不用选择a或b的,所有n个数字最多会加a或b，n-1次
        for(int j=0;j<n;j++)
        dp[i][j]=(dp[i-1][((j-(n-i)*a)%n+n)%n]%mod+dp[i-1][((j+(n-i)*b)%n+n)%n]%mod)%mod;
    cout<<dp[n-1][(s%n+n)%n]%mod<<endl;
    return 0;
}