【蓝桥杯】历届试题 波动数列

 

原题链接：http://lx.lanqiao.cn/problem.page?gpid=T122

问题描述

　　观察这个数列：

　　1 3 0 2 -1 1 -2 ...

 

　　这个数列中后一项总是比前一项增加2或者减少3。

 

　　栋栋对这种数列很好奇，他想知道长度为 n 和为 s 而且后一项总是比前一项增加a或者减少b的整数数列可能有多少种呢？

输入格式

　　输入的第一行包含四个整数 n s a b，含义如前面说述。

输出格式

　　输出一行，包含一个整数，表示满足条件的方案数。由于这个数很大，请输出方案数除以100000007的余数。

样例输入

4 10 2 3

样例输出

2

样例说明

　　这两个数列分别是2 4 1 3和7 4 1 -2。

数据规模和约定

　　对于10%的数据，1<=n<=5，0<=s<=5，1<=a,b<=5；

　　对于30%的数据，1<=n<=30，0<=s<=30，1<=a,b<=30；

　　对于50%的数据，1<=n<=50，0<=s<=50，1<=a,b<=50；

　　对于70%的数据，1<=n<=100，0<=s<=500，1<=a, b<=50；

　　对于100%的数据，1<=n<=1000，-1,000,000,000<=s<=1,000,000,000，1<=a, b<=1,000,000。

　

　　1、这道题如果用暴力搜索，铁定超时 时间复杂度 O（2^n）

　　2、转换思路，设第一个数为 x , 则以样例为例子，我们可以基于 （1）的思想画出状态图

　　　　　　　　

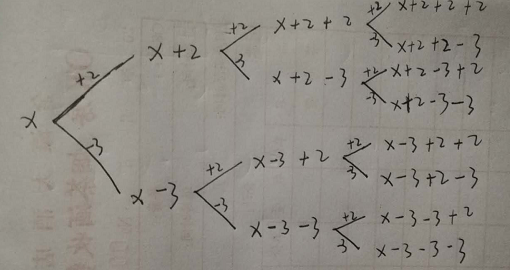
　　　　　　　　设 choice = { a, -b } = { 2, -3 }

从图中我们可以发现 s = x + (x + choice) +  (x + choice + choice)  + ( x + choice + choice + choice)   （1）

所以 等式（1）中  （a出现的次数 ） + （b出现的次数） =  1 + 2 + 3 + 。。。 + （n-1） = n（n-1）/2

所以 设 a 在等式（1）中出现的次数为 y , 则  b 在等式（1）中出现的次数为 n( n-1 )/2 - y

所以等式（1）可整理为 s = nx + ay - b( n(n-1)/2 - y )    <==>   s+b( n(n-1)/2 )  = nx + (a+b)y　         （2）

又因为  y  的取值范围 为  [ 0,  n(n-1)/2 ] ,  且 x ,  y 均为正数， 解方程（2）则可以求出 y (即a出现的次数) 的所有情况

----------------------------------------------

到这里题目完成了一半

对于y的每种情况，可能有不同的排序

由于y的特殊性 可以知道 y 的值是有要求的： 是集合 U = { 1， 2， 3， ......., n-1 } 的子集的所有元素之和

因此问题变成了 问 集合 U 中 有多少个子集符合要求

上述这个问题用dp解决

设dp（i，j）表示从集合U（假设集合中元素从小到大排列）中前 i 个数中选择，使得和为 j 总共有几种选择

　　　　　　　　　　　　（i）初始状态   dp[ 0 ] [ j ] = 0   dp[ i ][ 0 ] = 1 

　　　　　　　　　　　　（ii）状态转移方程

　　　　　　　　　　　　　　当 i > j 时， 此时第 i 个元素不可以选（因为选了的话元素之和肯定大于 j）  

　　　　　　　　　　　　　　　　　dp( i, j ) = dp( i-1, j )

　　　　　　　　　　　　　　当 i <= j 时， 第 i 个元素要么选， 要么不选

　　　　　　　　　　　　　　　　　dp( i, j ) = dp( i-1, j) + dp( i-1, j- i )

---------------------------------------------

　　　在这里 dp 可以利用滚动数组优化空间复杂度 (具体见代码)

#include<iostream>
#include<cstdio>
using namespace std;
const int MOD = 100000007;
const int maxn = 1000010;  
int dp[maxn];
int temp;
long long n, s, a, b;
void init(){
    dp[0] = 1;
    for(int i=1;i<n;++i){
        for(int j=i*(i+1)/2;j>=i;--j){        //此处j的起始值优化，找了好久 
            dp[j] = (dp[j] + dp[j-i])%MOD;
        }
    }
}

int main(){
    
    cin >> n >> s >> a >> b;
    temp = n*(n-1)/2;
    init();
    long long q = a + b;  
    s += temp*b;
        
    // 设x为第一个数  设 y 个 a    0=< y <= n(n-1)/2
    //解方程 s = nx + qy 整数解个数
    int ans = 0;
    for(int y=0;y<=temp;++y){
        long long tt = s - q * y;
        if(tt%n==0){
            ans = (ans + dp[y])%MOD;
        } 
    }
    printf("%d", ans);
    return 0;
}

 

转载于:https://www.cnblogs.com/chsobin/p/8406400.html