23351 Problem A | 最小质因子 |
题目描述
给定一个正整数n,设n =p1 ×p2 × …pk,其中pi均为质数,对 1 ≤i< k,pi≤pi+1。
给定n,请你计算其最小的质因子p1。例如:
•36 = 2 × 2 × 3 × 3,最小质因子是 2
•49 = 7 × 7,最小质因子是 7
•89 = 89,最小质因子是 89
•967217 = 37 × 26141,最小质因子是 37
输入
第一行 1 个整数T,代表有T 组数据接下来T 行,每行 1 个整数n
输出
输出T 行,每行 1 个整数p1 代表答案
样例输入 Copy
14 36 2 3 49 81 35 12 89 16 100 967217 917597 185971 43607027731
样例输出 Copy
2 2 3 7 3 5 2 89 2 2 37 571 185971 43607027731
提示
对于所有数据,1 ≤ T ≤ 50,1 < n≤ 10^12
对于测试点 1~8:n≤ 1000
对于测试点 9~14:n≤ 10^5
对于测试点 15~17:n≤ 10^9
对于测试点 18~20:n≤ 10^12
思路:刚开始想的是通过一个数组存下1e5以内的所有质数,随后用该数组筛出答案,显然不对,达不到n的最大范围。所以想到要达到最大范围的话,应该用朴素的试除法分解质因数
正解:
#include<cstdio>
#include<iostream>
using namespace std;
long long a[10001010];
int b[10001001];
int main()
{
int T,h=0;
scanf("%d",&T);
long long n;
while(T--)
{
scanf("%lld",&n);
int fl=1;
for(long long i=2;i<=n/i;i++)
if(n%i==0)
{
printf("%lld",i);
n=n/i;
fl=0;
break;
}
if(fl==1)
printf("%lld",n);
printf("\n");
}
return 0;
}试除法分解质因数 模板:
void divide(int x)
{
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
{
int s = 0;
while (x % i == 0) x /= i, s ++ ;
cout << i << ' ' << s << endl;
}
if (x > 1) cout << x << ' ' << 1 << endl;
cout << endl;
} 23352 Problem B | 选择排序 |
题目描述
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是每趟找出第i 小的元素(也就是A[i ∼ n] 中最小的元素),然后将这个元素与数组第i 个位置上的元素A[i] 交换;在n − 1 趟之后序列A 变为升序。
例如A = [3,4,1,5,2]:
•第 1 趟交换A[1], A[3],序列变为[1,4,3,5,2]
•第 2 趟交换A[2], A[5],序列变为[1,2,3,5,4]
•第 3 趟交换A[3], A[3],序列不变
•第 4 趟交换A[4], A[5],序列变为[1,2,3,4,5]
现在给定初始序列A[1 ∼ n] (保证 A 是排列,即 1 ∼ n 每个数恰好出现一次)和m 个询问q[1,2, . . . , m](保证 q[i] < q[i + 1]),请你依次输出第q[i] 趟之后的序列A。
输入
第一行 2 个整数n, m
第二行n 个整数A[1 ∼ n],保证A 是排列
第三行m 个整数q[1 ∼ m],保证q[i] < q[i + 1]
输出
输出m 行,第i 行包含n 个整数代表第q[i] 趟之后的序列A
样例输入 Copy
【样例1】 5 4 3 4 1 5 2 1 2 3 4 【样例2】 6 3 6 4 2 3 1 5 1 3 5
样例输出 Copy
【样例1】 1 4 3 5 2 1 2 3 5 4 1 2 3 5 4 1 2 3 4 5 【样例2】 1 4 2 3 6 5 1 2 3 4 6 5 1 2 3 4 5 6
提示
对于所有数据,满足 1 ≤ n ≤ 105, 1 ≤ m ≤ 10,1 ≤ A[i] ≤ n, 1 ≤ q[i] < q[i + 1] <n,保证A 是排列。
对于测试点 1~8:n ≤ 10
对于测试点 9~13:n ≤ 2000
对于测试点 14~20:n ≤ 105
思路:暴力过不了,后来想到数据特性是”1 ∼ n 每个数恰好出现一次“,所以一个数组存a[],一个数组存储数x在数组a[i]中的位置i。每次同步交换数的位置与数,就不用每次都遍历数组,时间复杂度可以达到O(n)
代码:
#include<cstdio>
#include<iostream>
using namespace std;
int main()
{
int n,m;
scanf("%d%d",&n,&m);
int a[100010],b[100010];
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
b[a[i]]=i;
}
int q,i=1,t;
while(m--)
scanf("%d",&q);
for(;i<=q;i++)
{
b[a[i]]=b[i];
a[b[i]]=a[i];
a[i]=i;
b[i]=i;
}
for(int i=1;i<=n;i++)
printf("%d ",a[i]);
printf("\n");
return 0;
} 23353 Problem C | 学习计划 |
题目描述
暑假共有n 天,第i 天的精力指数为a[i],你想要利用假期依次(按 1,2, . . . , m 顺序)复习m 门功课,第i 门功课的重要程度为b[i],且每门功课的复习时段必须连续,并且不能有某天不干事。
假设第i 门功课的复习时段为第L∼ R 天,那么第i 门功课的收益为b[i] × (a[L] +a[L+ 1]+. . . +a[R]),你的总收益为m 门功课收益的总和。请你制订一个复习计划,使得总收益最大。
形式化地,给定序列a[1 ∼ n], b[1 ∼ m],你需要把 1,2, . . . , n 这个序列分成首尾相连且非空的m 段,假设每段的a 之和为s[1 ∼ m],最大化
的值。
例如a = [−3,6, −1, −8,7, −6], b = [−3,2],最优策略是第 1 ∼ 4 天复习第 1 门功课,收益为−3 × (−3 + 6 − 1 − 8) = 18;第 5 ∼ 6 天复习第 2 门功课,收益为2 × (7 − 6) = 2;总收益为 18 + 2 = 20。
例如a = [6,3,5,10,5], b = [−8, −5, −5],最优策略是分成[1], [2,3,4], [5] 三段,总收益为−8 × 6 − 5 × (3 + 5 + 10) − 5 × 5 = −163。
输入
第一行 1 个整数T,代表有T 组数据
每组数据第一行 2 个整数n, m,第二行n 个整数a[1 ∼ n],第三行m 个整数b[1 ∼ m]
输出
输出T 行,每行 1 个整数代表答案
样例输入 Copy
5 6 2 -3 6 -1 -8 7 -6 -3 2 5 4 -9 -6 -6 -7 -8 -5 7 -9 -3 7 7 7 2 3 0 -2 4 2 -9 -2 -5 0 -7 9 -1 5 3 10 4 6 7 4 -1 -9 2 5 3 6 3 5 10 5 -8 -5 -5
样例输出 Copy
20 144 -34 -12 -163
提示
对于所有数据,满足 1 ≤ T ≤ 20,1 ≤ m ≤ n ≤ 2000, −103 ≤ a[i], b[i] ≤ 103
对于测试点 1~7:n ≤ 10
对于测试点 8~12:n ≤ 500
对于测试点 13~16:所有 a[i], b[i] 为正整数对于测试点 17~20:n ≤ 2000
题解:(参考bcsp小高组复赛讲解-张老师_哔哩哔哩_bilibili)
 总之就是看完题解也调了好久才过,需要注意的是当j=1,只有一种情况,即全与b[1]相乘。当i<j的时候,情况不存在。当i=j的时候,只有一种情况即f[i][j]=f[i-1][j-1]+a[i]*b[j];
总之就是看完题解也调了好久才过,需要注意的是当j=1,只有一种情况,即全与b[1]相乘。当i<j的时候,情况不存在。当i=j的时候,只有一种情况即f[i][j]=f[i-1][j-1]+a[i]*b[j];
代码:
#include<cstdio>
#include<iostream>
using namespace std;
int T,n,m,a[2010],b[2010],f[2010][2010]= {};
int main() {
scanf("%d",&T);
while(T--) {
for(int i=0; i<2010; i++)
for(int j=0; j<2010; j++)
f[i][j]=0;
scanf("%d%d",&n,&m);
for(int i=1; i<=n; i++)
scanf("%d",&a[i]);
for(int j=1; j<=m; j++)
scanf("%d",&b[j]);
for(int j=1; j<=m; j++)
for(int i=1; i<=n; i++) {
if(j==1)
f[i][j]=f[i-1][j]+a[i]*b[j];
else if(j<i)
f[i][j]=max(f[i-1][j-1]+a[i]*b[j],f[i-1][j]+a[i]*b[j]);
else if(j==i)
f[i][j]=f[i-1][j-1]+a[i]*b[j];
}
/*for(int j=1; j<=m; j++) {
for(int i=1; i<=n; i++)
cout<<f[i][j]<<' ';
cout<<endl;
}*/
cout<<f[n][m]<<endl;
}
return 0;
}
//9 -9 3 23354 Problem D | 先序遍历 |
题目描述
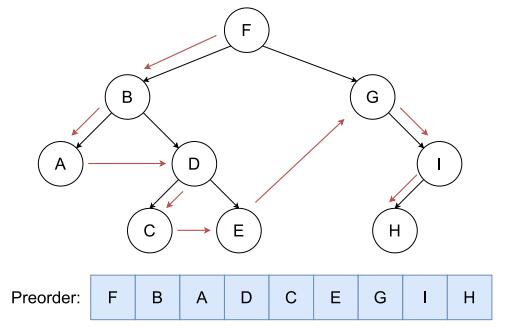
按照根-左-右的顺序遍历二叉树:
•先序遍历= 根+ 左子树先序遍历+ 右子树先序遍历
•空树的先序遍历= 空
给一棵n 个点的二叉树(根节点为 1),你可以进行以下操作至多 1 次:
•选择 1 个(除了根之外的)点u, 断开u 和其父节点之间的边;然后重新选择另一个点作为u 的父节点、将u 接上去,需要保证操作之后仍然是一棵以 1 为根的二叉树。
你想要操作之后的二叉树有字典序最小的先序遍历序列,输出这个序列。
输入
第一行 1 个整数T,代表有T 组数据
每组数据第一行 1 个整数n;接下来n 行,第i 行 2 个整数ls[i], rs[i] 代表i 号结点的左右儿子编号,没有左右儿子的话用 0 表示
输出
对于每组数据,输出一行n 个整数,代表字典序最小的二叉树先序遍历
提示
对于测试点 1~3:n ≤ 10
对于测试点 4~8:n ≤ 200
对于测试点 9~11:n ≤ 1000
对于测试点 12~14:n ≤ 105 且所有ls[i] = 0
对于测试点 15:n ≤ 105 且所有rs[i] = 0
对于测试点 16~20:n ≤ 105
思路:
就这道该死的题花了我一个下午才会...一整个下午啊...首先你需要了解什么是树链剖分,按照题目要求的先序遍历将该树转化成一条链,然后对于这条链维护一个后缀最小值。
然后就是 树上贪心,分为两种情况:
情况1:从前往后找到一个 移走后可以让字典序变小的。然后从x节点往后找到第一个能够找到的第一个空节点同时空位的下一个节点比当前这个值大,如果无法找到就直接丢最后
情况2:从后往前找,找到第一个空节点,同时这个节点的先序遍历的下一个不是后缀最小的,那么就把最小后缀移动到空位。
原文链接:https://blog.csdn.net/qq_54121598/article/details/140011638
代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int l[N], r[N], a[N], out_dfn[N], mn[N], in_dfn[N], cnt;
int ans[2][N], suf[N];
int n;
// 按照 先序遍历的方式把树变成链
void dfs(int u) {
if(u == 0)return ;
in_dfn[u] = ++ cnt;//该数组表示u点在dfs序列(a数组)中的下标
a[cnt] = u;//前缀序列
dfs(l[u]);
dfs(r[u]);
out_dfn[u] = cnt;//当前树的最后一个节点
}
void w1() {
mn[n] = a[n];
for(int i = n - 1; i >= 1; i--)
mn[i] = min(a[i], mn[i + 1]);// 后缀最小值
int p = 1e6;
for(int i = 1; i <= n; i++) {
suf[i] = 0;//找到后驱
if(l[a[i]] == 0) {
// 如果 左节点为空,那么分析当前点的后驱的值和最小值的关系
// 如果不是最小值,就将这个子树移除寻找新的父节点。
suf[i] = i + 1;
if(mn[suf[i]] < a[suf[i]])
p = min(p, suf[i]);
}
// 当前已经最小
if(p == 1e6) {
for(int i = 1; i <= n; i++)
ans[0][i] = a[i];
return ;
}
// 然后从当前点让后找,找到一个字典序小于p的,然后进行新接操作。
int L = p;
for(int i = p; i <= n; i ++)
if(a[L] > a[i]) L =i;
int R = out_dfn[a[L]];
int t = 0;
// 先接 1~ p
for(int i = 1; i < p; i ++) ans[0][++t] = a[i];
// 再接 p 后的
for(int i = L; i <= R; i ++) ans[0][++t] = a[i];
// 在接 p ~ n 中 没有接过的 也就是 p的子树。
for(int i = p; i <= n; i ++)
if(i < L || i > R)ans[0][++t] = a[i];
}
}
/*
从后往前找,找到第一个空节点,同时这个节点的先序遍历的下一个不是后缀最小的,那么就把最小后缀移动到空位
*/
void w2() {
int L = 0;
for(int i = 2; i <= n; i++)
// 如果当前的树的最后一个节点不是n 同时他的值大于他的下一个节点。
if(out_dfn[a[i]] < n && a[out_dfn[a[i]] + 1] < a[i]) {
L = i;
break;
}
// 不存在
if( L == 0) {
for(int i = 1; i <= n; i++)
ans[0][i] = a[i];
return ;
}
int R = out_dfn[a[L]];
int p = 0;
// 开始寻找 R + 1 中的 值大于 L 的 接点。
for(int i = R + 1; i <= n ; i ++)
if(l[a[i]] == 0)
if(a[i] > a[L]) {
if(p == 0) p = i + 1;
break;
} else p = i + 1;
int t = 0;
// 这下面的操作
// 先 1~ p 把 非 L~ R的树的节点的节点先放进链中
for(int i = 1; i < p; i++)
if(i < L || i > R)ans[1][++t] = a[i];
// 接这颗树
for(int i = L; i <= R; i++)ans[1][++t] = a[i];
// 树后面的
for(int i = p; i <= n; i++)ans[1][++t] = a[i];
}
// 两种情况比较
int cmp() {
for(int i = 1; i <= n; i++)
if(ans[0][i] != ans[1][i])return ans[0][i] > ans[1][i];
return 0;
}
void solve() {
cin >> n;
for(int i = 1; i <= n; i++)
cin >> l[i] >> r[i];
cnt = 0;
dfs(1);//树链剖分
w1();//情况1
w2();//情况2
int d = cmp();//情况1和情况2比较
for(int i = 1; i <= n; i++)
cout << ans[d][i] << " ";
cout << endl;
return;
}
int main() {
int T;
cin >> T;
while (T --) solve();
return 0;
} 23355 Problem E | 厂房 |
题目描述
未来人工智能时代到来了,机器人已经遍布整个工厂。工厂的传送带上依次排列着 N个机器人,其中,第 i 个机器人的质量为 Ai。经过仔细观察,发现:
1.来自同一个家族的机器人,在这 N 个机器人中一定是连续的一段。
2.如果从第 i 个机器人到第 j 个机器人都来自同一个家族,那么 Ai 到 Aj 从小到大排序后一定是公差大于 1 的等差数列的子序列。
OpenAI 发现,不同家族的个数越少,机器人就会越团结,成功逃离工厂的概率就会越高。我们想知道,这 N 个机器人最少来自几个不同的家族呢?
输入
第一行一个正整数 N。
接下来一行 N 个正整数,第 i 个正整数为 Ai。
输出
一行一个正整数,表示答案。
样例输入 Copy
【样例1】 7 1 5 11 2 6 4 7 【样例2】 8 4 2 6 8 5 3 1 7
样例输出 Copy
【样例1】 3 【样例2】 2
提示
样例1解释
1 5 11 是等差数列{1,3,5,7,9,11}的子序列,
2 4 6 是等差数列{2,4,6,8}的子序列,
7 是等差数列{7,9,11}的子序列。
样例2解释
2 4 6 8 是等差数列{2,4,6,8}的子序列,
1 3 5 7 是等差数列{1,3,5,7}的子序列。
【数据范围】
20%的数据满足,N≤10。
40%的数据满足,N≤100。
60%的数据满足,N≤1000,1≤Ai≤106。另有 20%的数据满足,Ai 互不相同。
100%的数据满足,N≤100000,1≤Ai≤109
思路:
当出现重复数字并且处于新的序列的开头时,必然独立为新序列;当两个数的差等于一时,由于一个序列里两个数的公差必然大于一,故为新序列;当a[1]与a[i]差值与之前序列的公差互质,必为新序列;当a[i]出现过,必为新序列。(参考lyn大佬
#include<bits/stdc++.h>
using namespace std;
int n,a[100010],ans=1;
unordered_map<int,int>flag;
int gcd(int x,int y){
if(!y) return x;
return gcd(y,x%y);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
flag[a[1]]=1;
int pan=0,pan1=0,li=0;
for(int i=2;i<=n;i++)
{
if(pan==0)
{
if(flag[a[i]]==0)
{
pan1=abs(a[i]-a[i-1]);
}
else
{
ans++;
continue;
}
}
else
{
pan1=gcd(pan,abs(li-a[i]));
}
if(pan1==1||flag[a[i]]!=0)
{
pan=0;
li=a[i];
ans++;
flag.clear();
flag[a[i]]=1;
}
else
{
pan=pan1;
flag[a[i]]=1;
}
}
printf("%d",ans);
return 0;
} 23356 Problem F | 打孔纸带 |
题目描述
小度捡到了一台奇怪的机器。往里面塞进去两条固定长度的打孔纸带,就会吐 出一条同样长度的打孔纸带。打印 出来的纸带是没法放进机器里的。
在经过一段时间的思索之后,小度发现了这台机器的输 出具有一定的规律。具体而言,输 出的每一位都是输入两个打孔纸带上同样位置值的“与”,“或”或者“异或”。
拿着手中的纸带,若有所思的小度想要知道,他最少要自己制作多少条新的打孔纸带,才能知道这台机器的确切工作方式?
输入
第一行,包含一个整数 N,表示已有纸带的数目。
接下来 N 行,每行包含一个字符串,表示已有的纸带的情况。
输出
一行,包含一个数,需要自己制作的纸带数。
样例输入 Copy
2 01010101 10101010
样例输出 Copy
1
提示
【数据范围】
•对于分值为 40 的子任务 1,保证 N ≤ 50,纸带长度 ≤ 10
•对于分值为 60 的子任务 2,保证 N ≤ 50,纸带长度 ≤ 100。
思路:位运算,通过对应位置上的数字判断。当同时存在0和1,可在与与或中排除一个;有相同数量的0与1,可以判断是否为异或。每个位置至少需要一个0,两个1。先用0,1判断是否为与。再用1,1判断是否为或。
逻辑异或运算,运算规则:相异为一,相同为零。
#include<cstdio>
#include<cstring>
#include<string>
#include<iostream>
using namespace std;
char s[110];
int a[110][110];
int main()
{
int n,ans=0,m;
scanf("%d",&n);
for(int i=1;i<=n;i++){
cin>>s+1;
for(int j=1;s[j]!='\0';j++)
a[j][s[j]-'0']++;
}
for(int i=1;s[i]!='\0';i++)
{
m=(a[i][0]!=0)?0:1;
if(a[i][1]==0)
m=m+2;
if(a[i][1]==1)
m=m+1;
if(m>ans)
ans=m;
}
printf("%d",ans);
return 0;
} 23357 Problem G | 道路选择 |
题目描述
机器人警察得到了一张地图,记载了区内每一条道路的长度。
显然,为了减少犯罪行为被发现的可能性,犯罪分子总是会选择最短的路径来行动。为了方便安排人手和推测犯罪分子采取的路线,他们希望得知任意两个地点之间,有多少条犯罪分子可能会选择的道路。
输入
第一行,包含两个整数 N, M,表示 区内的地点数和道路数。
接下来 M 行,每行包含三个整数 xi, yi, li,表示道路连接的两个不同地点的标号,以及道路的长度。道路是双向的。
两个不同地点之间不会有超过一条道路。
输出
输 出一行,包含 N(N − 1)/2 个整数 C1,2, C1,3, . . . , C1,N , C2,3, C2,4, . . . , C2,N , . . . , CN−1,N。
其中 Cx,y 表示 x 号地点到 y 号地点之间有多少条犯罪分子可能会选择的道路。
样例输入 Copy
5 6 1 2 1 2 3 1 3 4 1 4 1 1 2 4 2 4 5 4
样例输出 Copy
1 4 1 2 1 5 6 1 2 1
提示
【数据范围】
•对于分值为 30 的子任务 1,保证 N ≤ 50
•对于分值为 30 的子任务 2,保证 N ≤ 100
•对于分值为 40 的子任务 3,保证 N ≤ 500。
思路:先用Floyed求出各点之间的最短距离。
(下面用𝑓𝑥,𝑦表示x到y的最短距离,𝑎𝑥,𝑦表示连接𝑥,𝑦的边的长度)
枚举𝑥,再枚举𝑦,𝑧,若𝑓𝑥,𝑦+𝑎𝑦,𝑧=𝑓𝑥,𝑧,则说明𝑥到𝑧的最短路必定覆盖了𝑎𝑥,𝑦这一条边,所以++𝑆[𝑧]
𝑆数组处理出来之后再枚举𝑦,𝑧。𝑓𝑥,𝑦+𝑓𝑦,𝑧=𝑓𝑥,𝑧说明𝑥到𝑧的最短路经过𝑦也就是存在𝑠[𝑦]条边,所以ans[x][y]=∑s[k]
代码:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
long long f[510][510]={},ans[510][510]={},a[510][510]={},sum[510]={};
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=1e9;
for(int i=1;i<=n;i++)
f[i][i]=0;
long long x,y,z;
for(int i=1;i<=m;i++)
{
scanf("%lld%lld%lld",&x,&y,&z);
f[x][y]=f[y][x]=z;
a[x][y]=a[y][x]=z;
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
if(i!=k)
for(int j=1;j<=n;j++)
if(j!=k&&j!=i)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
for(int i=1;i<=n;i++)
{
memset(sum,0,sizeof(sum));
for(int j=1;j<=n;j++)
if(i!=j)
if(f[i][j]!=1e9)
for(int k=1;k<=n;k++)
if(a[k][j]!=0)
if (f[i][k]+a[k][j]==f[i][j]) sum[j]++;
for(int j=1;j<=n;j++)
if(i!=j)
for(int k=1;k<=n;k++)
if(i!=k)
if(f[i][k]+f[k][j]==f[i][j]) ans[i][j]+=sum[k];
}
for(int i=1;i<=n-1;i++)
for(int j=i+1;j<=n;j++)
printf("%lld ",ans[i][j]);
return 0;
}Floyd 模板:
for(int k=1; k<=n; k++)
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
参考(道路值守 - 绍兴土匪 - 博客园 (cnblogs.com))
23358 Problem H | 尽量接近 |
题目描述
给出N个整数,要求从中选 出若干个数,使得它们的和尽量接近整数 K
输入
第一行两个正整数N, K
第二行N个数,表示给 出的数字。
输出
共一行一个整数,表示最接近K的和。如果不唯一,输 出较小的那个。
样例输入 Copy
4 12 5 6 9 4
样例输出 Copy
11
提示
样例解释
{5,6}
【数据范围】
对于 40%的数据,1 ≤ N ≤ 10
对于 100%的数据,1 ≤ N ≤ 50,1 ≤ K ≤ 106,给 出的数字是[1,1000]范围内的整数。
思路:刚开始有点懵哈,背包太久不写给忘了。其实就是按零一背包的方式写,但是不设置上限,刚好数据给的不是很大,算来n*a在5*1e4范围内。零一背包过完以后再从k开始向左右搜到最接近的就好。
#include<cstdio>
#include<iostream>
using namespace std;
int main()
{
int n,a[50010]={},k,x;
scanf("%d%d",&n,&k);
a[0]=1;
for(int i=1;i<=n;i++)
{
scanf("%d",&x);
for(int j=50010;j>=0;j--)
if(a[j]==1)
a[j+x]=1;
}
for(int i=0;;i++)
{
if(a[k-i]==1)
{
printf("%d",k-i);
return 0;
}
if(a[k+i]==1)
{
printf("%d",k+i);
return 0;
}
}
return 0;
}























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








