10.2日多校联考第一场

考试时间安排及策略

8:00 - 8:30      签到A题做完
8:35 - 9:00      浏览剩下的题面，没啥思路
9:00 - 9:40      看了10min B 题，会了。写了一发，冲过了大样例
9:50 - 10:20      想到了 C 题 52pts 的做法
10:20 - 10:50      码完了 C题 52pts 做法， 冲过了样例，感觉没什么问题，交了一发，先扔了
10:50 - 11:20      想 D 题，一直没有啥思路
11:20 - 11:50      灵光一现，感觉D题答案的图像是一个单峰函数，写一个三分再套一个二分好像没什么问题，复杂度也就多一个log。并且也可以通过一些技巧去重。果断开写。写完后过了样例，并且把大样例也跑出来了，但是跑了整整10s。感觉要寄。

考试结果

A题过掉了
B题过掉了
C题52pts，没有挂分
D题爆0了， 大红大黄 ，复杂度高的离谱。
总分252，rk1。

考试反思

A.正向思考不行可以多进行反向思考。
B.要多使用技巧，并且要会计算复杂度。
C.要多类比之前的题目，要敢猜性质和结论。
D.不要太相信自己的正解做法，时间充足的情况下还是要先写分段，保证把暴力分拿到手。双指针和启发式合并还得多练练。

题解

A.滑雪

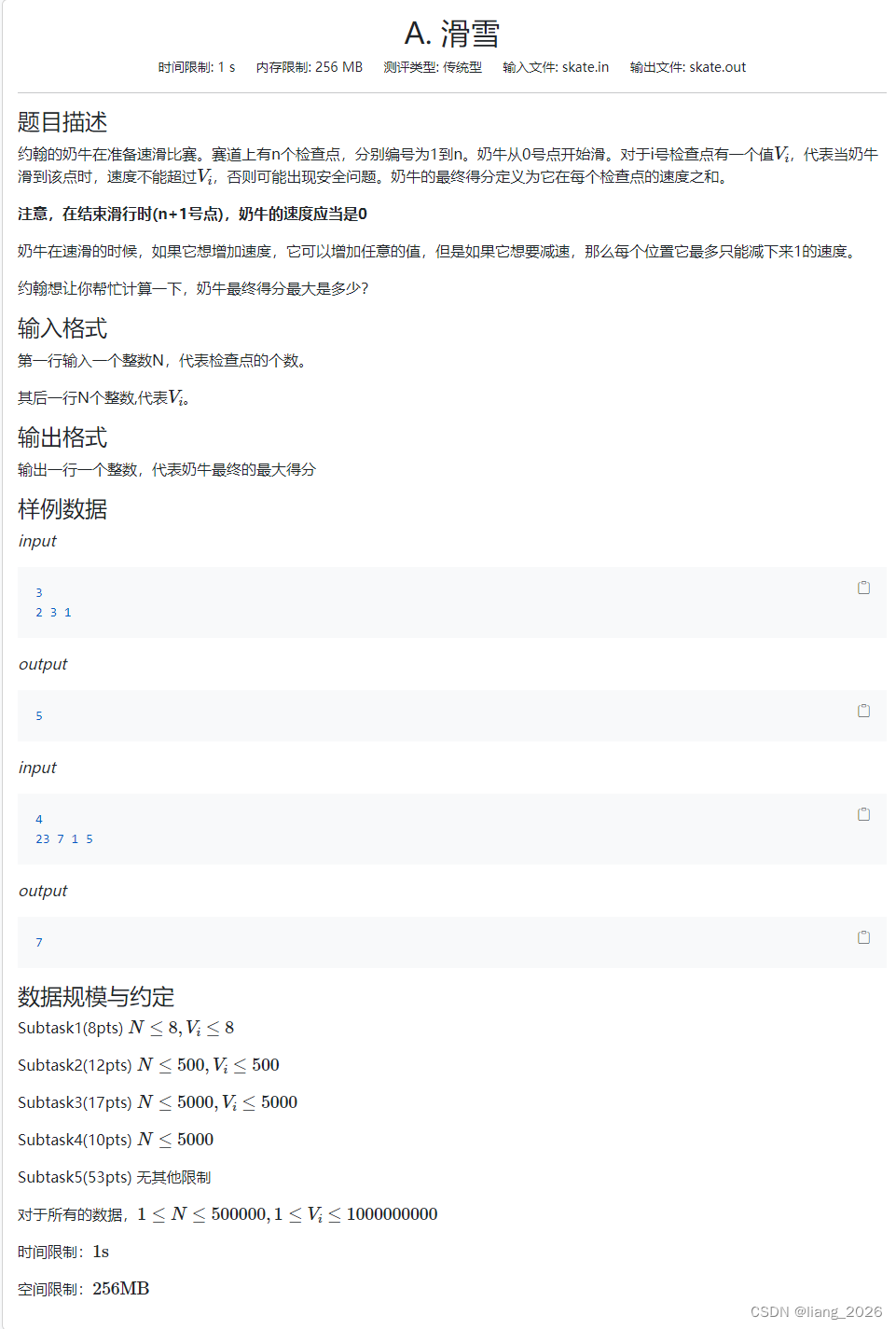
分析：每个点上的最大速度限制，实际上是在限制上一个点的最大速度。从后往前依次确定每个点上的速度。确定方法为 $a[i]=min(a[i+1],v[i])$。特别的，$a[n+1]=0$。最后累加 $a$ 即可。

B.农场道路修建

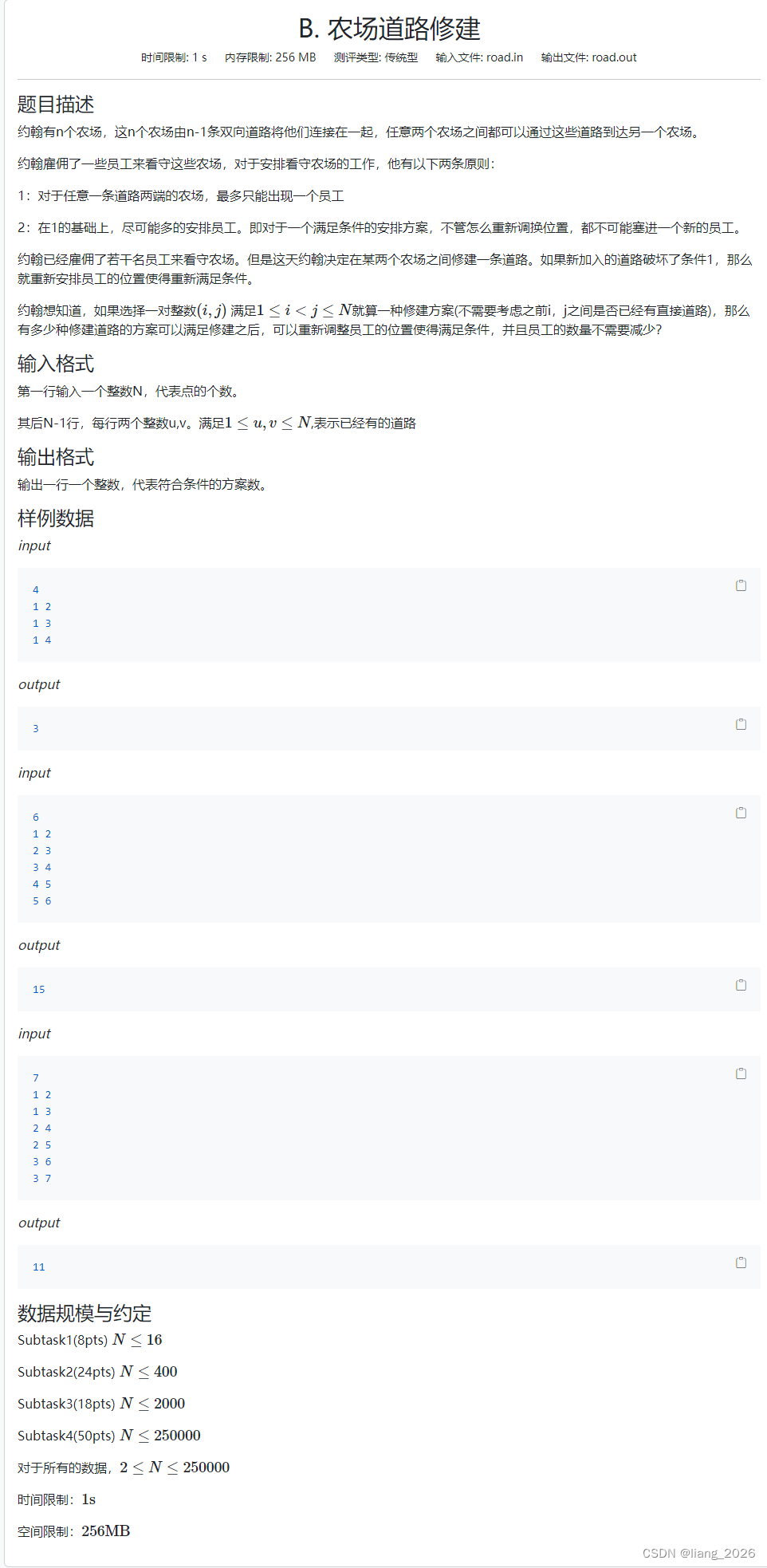
一句话题意： 对于给定的一棵树，求有多少个点对 $(u,v)$ 满足在 $(u,v)$ 之间连一条边后所形成的基环树与原来的树最大点独立集的大小相同。

分析： 我们可以把原树上的点分成两类： 1.必须要选的   \,   \, 2.可以不选的（包含一定不选的）。如果一个点对中有一个点可以不选，那么这个点对就是合法的。设可以不选的点的数量为 $cnt$，那么答案就是 $cnt\ast (cnt-1)/2+(n-cnt)\ast cnt$。

            我们考虑如何求 可以不选的点的数量。我们思考一下在求最大点独立集的过程设计的状态 ：$dp[x][0/1]$ 表示以 $x$ 为根的子树中， 不选/选 $x$ 号点的最大独立集大小。最后的答案就是 $max(dp[1][0],dp[1][1])$。我们可以通过 每个状态的转移来源确定某一个点是否在某一种最优方案中不被选中。

            具体来讲，我们可以反向做DP的过程，保证每一步都是可以转移到最优答案上的，然后如果 $dp[x][0]$ 可以转移到答案上，我们对 $x$ 打上标记。 同时还要写一个记忆化防止重复搜索，时间复杂度 $O(n)$。

CODE：

#include<bits/stdc++.h>//考虑将点分成两类，可以不放的和必须要放的 
#define pb push_back
using namespace std;//答案就是乘一下 
typedef long long LL;
const int N = 250010;
int n, u, v, dp[N][2], flag[N], num;
vector< int > E[N];
LL cnt0, cnt1;
bool vis[N];
bool bok[N][2];//表示这个状态是否搜过 
void dfs(int x, int fa){
	dp[x][1] = 1; dp[x][0] = 0;
	for(auto v : E[x]){
		if(v == fa) continue;
		dfs(v, x);
		dp[x][0] += max(dp[v][0], dp[v][1]);
		dp[x][1] += dp[v][0];
	}
}
void Get(int x, int fa, int f){//f 代表父亲的状态
    if(bok[x][f]) return ;//搜过直接回去即可 
	bok[x][f] = 1; 
	if(!f){//没有放  放不放都可以 
		if(dp[x][0] > dp[x][1]){
			flag[x] = 1;//可以不放
			for(auto v : E[x]){
				if(v == fa) continue;
				Get(v, x, 0);//必须往下传递不放的 
			} 
		}
		else if(dp[x][1] > dp[x][0]){
			for(auto v : E[x]){
				if(v == fa) continue;
				Get(v, x, 1);//必须传递放的 
			}
		}
		else{//一样就是放不放都可以 
		    flag[x] = 1;
		    for(auto v : E[x]){
		    	if(v == fa) continue;
		    	Get(v, x, 0);//不放
				Get(v, x, 1);//放都需要试一试 
			}
		}
	}
	else{//放了 只能不放 
	    flag[x] = 1;
		for(auto v : E[x]){
			if(v == fa) continue;
			Get(v, x, 0);
		}
	}
	return ;
}
int main(){
	freopen("road.in", "r", stdin);
	freopen("road.out", "w", stdout);
	scanf("%d", &n);
	for(int i = 1; i < n; i++){
		scanf("%d%d", &u, &v);
		E[u].pb(v);
		E[v].pb(u);
	}
	dfs(1, 0);
	Get(1, 0, 0);
	for(int i = 1; i <= n; i++){
		if(flag[i]) cnt0++;
		else cnt1++;
	}
	cout << (((cnt0 - 1LL) * cnt0) / 2LL) + (cnt0 * cnt1) << endl;
	return 0;
}

C.密码锁

分析： 考场上想出 $52pts$ 思路。

        我们考虑 $Subtask1,subtask2,subtask4$ 的做法：我们可以用线段树动态维护答案。

        具体来讲，我们对于线段树的每个节点维护一个 $num[5][5]$ 数组。$num[x][y]$表示这个节点对应的区间左端点字符是 $x$，右端点是 $y$ 的最小修改次数。转移也比较简单，枚举左儿子的右端点放什么字符，右儿子的左端点放什么字符进行转移即可。时间复杂度 $O(|S|lo{g}_2|S|\ast 625)$。卡一卡应该可过。

        正解： 正解是对上述算法的一个优化，是基于一条性质：

         设 $F(S)$ 表示 $S$ 这个字符串最后变成单调不降字符串的最小代价，设 $b(S,i)$ 表示将 $S$ 在 $i$ 规则下变成的 $01$ 字符串。 $i$ 规则是指 若$S_j\ge i$，则 $j$ 位置变成 $1$，否则为 $0$。那么有 $F(S)={\sum }_{i{=}^{\prime }{a}^{\prime }}^{{}^{\prime }{z}^{\prime }}F(b(S,i))$。

         下面证明一下这个性质：

         第一步：证明 $F(S)\ge {\sum }_{i{=}^{\prime }{a}^{\prime }}^{{}^{\prime }{z}^{\prime }}F(b(S,i))$。

         若 $S$ 变成 $S^{\prime }$ 是最优的变换方案：首先 $b(S^{\prime },i)$ 一定是一个合法的字符串。我们考虑 使用 $S$ 变成 $S^{\prime }$ 所花费的代价把每个 $b(S,i)$ 变成合法的字符串，这样即可证明 $F(S)\ge {\sum }_{i{=}^{\prime }{a}^{\prime }}^{{}^{\prime }{z}^{\prime }}F(b(S,i))$。那么对于 $S_j$ 变成了 $S_j^{\prime }$，它所需要的代价为 $|S_j-S_j^{\prime }|$，而只有当 $min(S_j,S_j^{\prime })<i\le max(S_j,S_j^{\prime })$ 时， $b(S,i)$ 和 $b(S^{\prime },i)$ 在该位置才不同，需要1个花费将他们变成相同。也就是说我可以将 $|S_j-S_j^{\prime }|$ 的花费用于调动 一些 $b(S,i)$ 的 $j$ 位置，使每个 $b(S,i)$ 的 $j$ 位置都变得合法。因此 使用 $S$ 变成 $S^{\prime }$ 的代价足够将每一个 $b(S,i)$ 变得合法。       所以 $F(S)\ge {\sum }_{i{=}^{\prime }{a}^{\prime }}^{{}^{\prime }{z}^{\prime }}F(b(S,i))$

         第二步：证明 ${\sum }_{i{=}^{\prime }{a}^{\prime }}^{{}^{\prime }{z}^{\prime }}F(b(S,i))\ge F(S)$。

         我们考虑设 $b(S,i)$ 变成 字符串$G_i$ 是最优合法变换。那么每个 $G_i$ 一定是前面若干个 $0$，后面全是 $1$。我们设 $le{n}_i$ 表示 $G_i$ 的前缀 $0$ 的个数。跟之前的证法类似，我们考虑所有 $b(S,i)$ 变成 $G_i$ 花费的代价之和是否能够调动 $S$ 使其变成一个合法的字符串。

        分情况讨论：

        1. 若 $le{n}_i$ 单调递增。那么我们考虑在 $[le{n}_i,le{n}_{i+1})$ 的位置放字符 $i$ （字符串从 $0$ 开始）。则这样构造出来的字符串单调不降，并且 $S$ 变成它的代价 与 每个 $b(S,i)$ 变成 $G_i$ 的代价和相同。

        为什么呢？

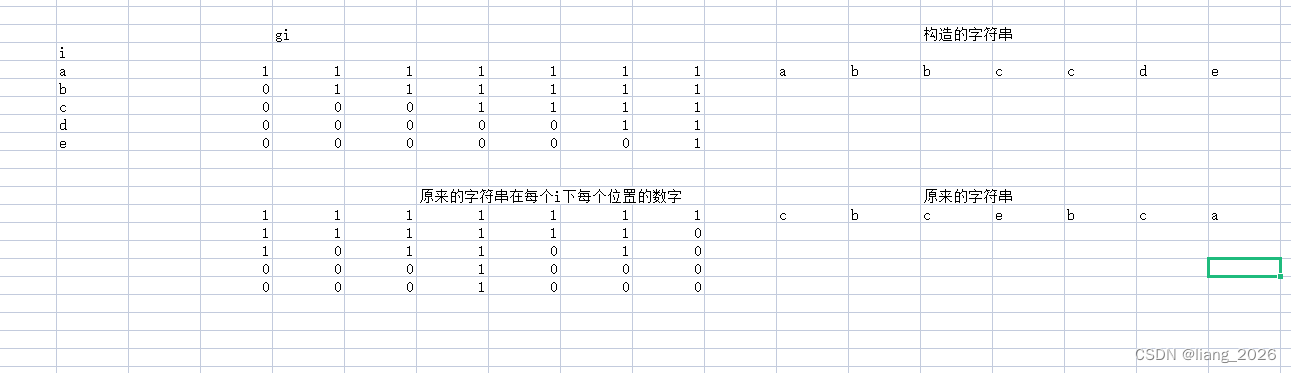
         纵向去看，我们发现 $S$ 变成构造出来的字符串的代价实际上就是上下 $1$ 的位置之差，而这个差值同样是 $b(S,i)$ 变成 $G_i$ 的过程中每一个位置所需要的代价和，满足这个相等也就可以保证 $S$ 变成构造出来的字符串的代价和 每个 $b(S,i)$ 变成 $G_i$ 的代价之和相等。

         2.若 $le{n}_i$ 并不单调递增。 如果 $le{n}_j>le{n}_{j+1}$，那么我们可以交换 $G_j$ 和 $G_{j+1}$，交换是只优不劣的。 因为对于 $G_j$ 是 $0$ 而 $G_{j+1}$ 是 $1$ 的位置 $k$ 而言，$b(S,j)$ 的第 $k$ 位和 $b(S,j+1)$ 的第 $k$ 位构成的二元组只有 $(1,0)$，$(1,1)$， $(0,0)$，交换后可以发现代价不会增大。因此 可以交换使得 $le{n}_i$ 单调递增。

         因此我们证明了 ${\sum }_{i{=}^{\prime }{a}^{\prime }}^{{}^{\prime }{z}^{\prime }}F(b(S,i))\ge F(s)$。

        所以 $F(S)={\sum }_{i{=}^{\prime }{a}^{\prime }}^{{}^{\prime }{z}^{\prime }}F(b(S,i))$

        我们根据这个性质，做26遍 $52pts$ 的做法即可。时间复杂度 $O(|S|lo{g}_2|S|\ast 8\ast 26)$。

CODE：

#include<bits/stdc++.h>//考虑用线段树维护 
using namespace std;//52pts
const int N = 1e5 + 10;
struct SegementTree{
	int l, r, num[2][2];
	#define l(x) t[x].l
	#define r(x) t[x].r
	#define num(x, i, j) t[x].num[i][j]
}t[N * 4];
int q, pos[N], len, res[N];
char str[N], c[N];
int get(int x, int y){
	return abs(x - y);
}
void build(int p, int l, int r){
	l(p) = l, r(p) = r;
	for(int i = 0; i < 2; i++)
	    for(int j = 0; j < 2; j++)
		    num(p, i, j) = 0x3f3f3f3f;
	if(l == r) return ;
	int mid = (l + r >> 1);
	build(p << 1, l, mid);
	build(p << 1 | 1, mid + 1, r);
}
void update(int p){
	for(int i = 0; i < 2; i++)
	    for(int j = 0; j < 2; j++)
	        num(p, i, j) = 0x3f3f3f3f;
	for(int i = 0; i < 2; i++)
		for(int j = i; j < 2; j++)
		    for(int k = i; k <= j; k++)
		        for(int l = k; l <= j; l++)
		            num(p, i, j) = min(num(p, i, j), num(p << 1, i, k) + num(p << 1 | 1, l, j));
}
void ins(int p, int pos, int c){
	if(l(p) == r(p)){
		num(p, c, c) = 0;
		for(int i = 0; i < 2; i++) num(p, i, i) = get(c, i);
		return ;
	}
	int mid = (l(p) + r(p) >> 1);
	if(pos <= mid) ins(p << 1, pos, c);
	else ins(p << 1 | 1, pos, c);
	update(p);
}
int query(int p){
	int res = 0x3f3f3f3f;
	for(int i = 0; i < 2; i++)
		for(int j = i; j < 2; j++)
			res = min(res, num(p, i, j));
	return res;
}
int main(){
	freopen("lock.in", "r", stdin);
	freopen("lock.out", "w", stdout);
	scanf("%s", str + 1);
	len = strlen(str + 1);
	scanf("%d", &q);	
	for(int i = 1; i <= q; i++)//离线存下来 
		scanf("%d\n%c", &pos[i], &c[i]);
	for(int i = 0; i < 26; i++){
		build(1, 1, len);
		for(int j = 1; j <= len; j++){
			ins(1, j, ((str[j] - ('a' + i) >= 0) ? 1 : 0));
		}
		res[0] += query(1);
		for(int j = 1; j <= q; j++){
			ins(1, pos[j], c[j] - ('a' + i) >= 0 ? 1 : 0);
			res[j] += query(1);
		}
	}
	for(int i = 0; i <= q; i++) printf("%d\n", res[i]);
	return 0;
}

D.奶牛打电话

还不太会