Diffie-Hellman密钥交换协议

Diffie-Hellman密钥交换协议

前言

在现代通信中，安全性是一个至关重要的因素。为了确保数据在传输过程中不被窃取或篡改，必须对数据进行加密。而加密的关键在于密钥的安全交换。Diffie-Hellman密钥交换协议（DH协议）是一种安全的密钥交换方法，广泛应用于网络安全领域。本文将详细介绍Diffie-Hellman密钥交换协议的基本原理和密钥协商过程。

基本原理

密钥交换协议

密钥交换协议是一种允许两方（通常是通信双方）在不安全的通信信道上安全地交换加密密钥的方法。传统的对称加密算法依赖于事先共享的密钥，而公钥加密算法虽然解决了密钥分发的问题，但其计算复杂度较高，不适合大数据量的加密传输。Diffie-Hellman密钥交换协议正是为了解决这一问题而设计的。

Diffie-Hellman密钥交换协议

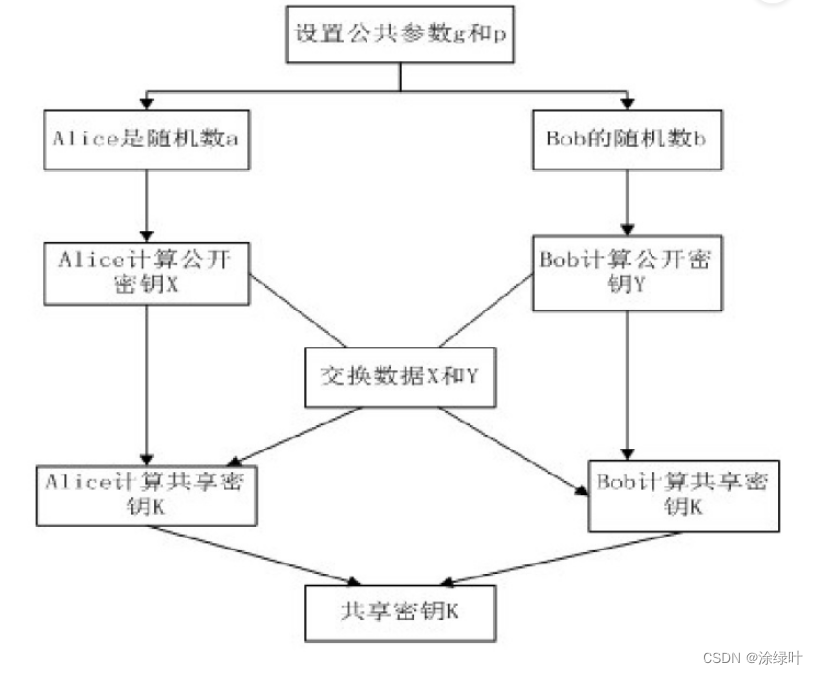
Diffie-Hellman密钥交换协议由Whitfield Diffie和Martin Hellman于1976年提出。该协议允许双方通过交换一些公开信息，在不安全的信道上协商出一个共同的秘密密钥，且无需预先共享密钥。其基本步骤如下：

假设双方为Alice和Bob共享一个素数q，以及整数a（a<q）,且a是q的原根

1.选择参数：Alice产生一个私钥$X_A$,$X_A<q$；Bob产生一个私钥$X_B$,$X_B<q$。

2.生成私钥和公钥：Alice计算公钥$Y_A=a^{X_A}modq$；Bob计算公钥$Y_B=a^{X_B}modq$；

3.交换公钥：Alice收到Bob计算的$Y_B$；Bob收到Bob计算的$Y_A$；

4.计算共享密钥：Alice计算共享密钥$K=Y_B^{X_A}modq$；Bob计算共享密钥$K=Y_A^{X_B}modq$；

协议框图

安全性能

Diffie-Hellman密钥交换协议是一种有效的密钥交换方法，可以在不安全的信道上安全地协商出一个共享密钥。通过公开素数 q 和基数 a，以及各自的私钥计算得到的公钥，双方可以在不泄露私钥的情况下，计算出相同的共享密钥，从而实现安全通信。这一协议的安全性依赖于离散对数问题的难解性，因此在选择参数时应尽量选择较大的素数 q 以增强安全性。

安全性分析

1. 离散对数问题：Diffie-Hellman协议的安全性基于离散对数问题的难度，即在已知 $Y_A=a^{X_A}modq$和 q 的情况下，计算$X_A$是非常困难的。这使得即使攻击者截获了公开的 q 和 a 以及交换的公钥 $Y_A$ 和 $Y_B$，也难以计算出共享密钥K。
2. 中间人攻击：虽然Diffie-Hellman协议可以防止被动攻击（即窃听），但它对主动攻击（如中间人攻击）是脆弱的。攻击者可以冒充双方进行独立的密钥交换。为了防止这种攻击，协议通常与其他认证机制（如数字签名或公钥基础设施）结合使用。
3. 参数选择：选择合适的素数 q 和基数 a 对于协议的安全性至关重要。应选择足够大的 q 以防止穷举攻击。此外，a 应该是 q 的原根，以确保能够生成所有可能的值。