树的先序（后序）中序构建二叉树 和树遍历+求树的深度和高度

目录

1.树的先序（后序）中序构建二叉树

 2.先序中序后序递归遍历树:

 3.树的层次遍历

4.判断树的高度和深度:

5.树的销毁

---

1.树的先序（后序）中序构建二叉树

树的先序遍历：

根 左 右

树的中序遍历：

左 根 右

树的后序遍历

左 右 根

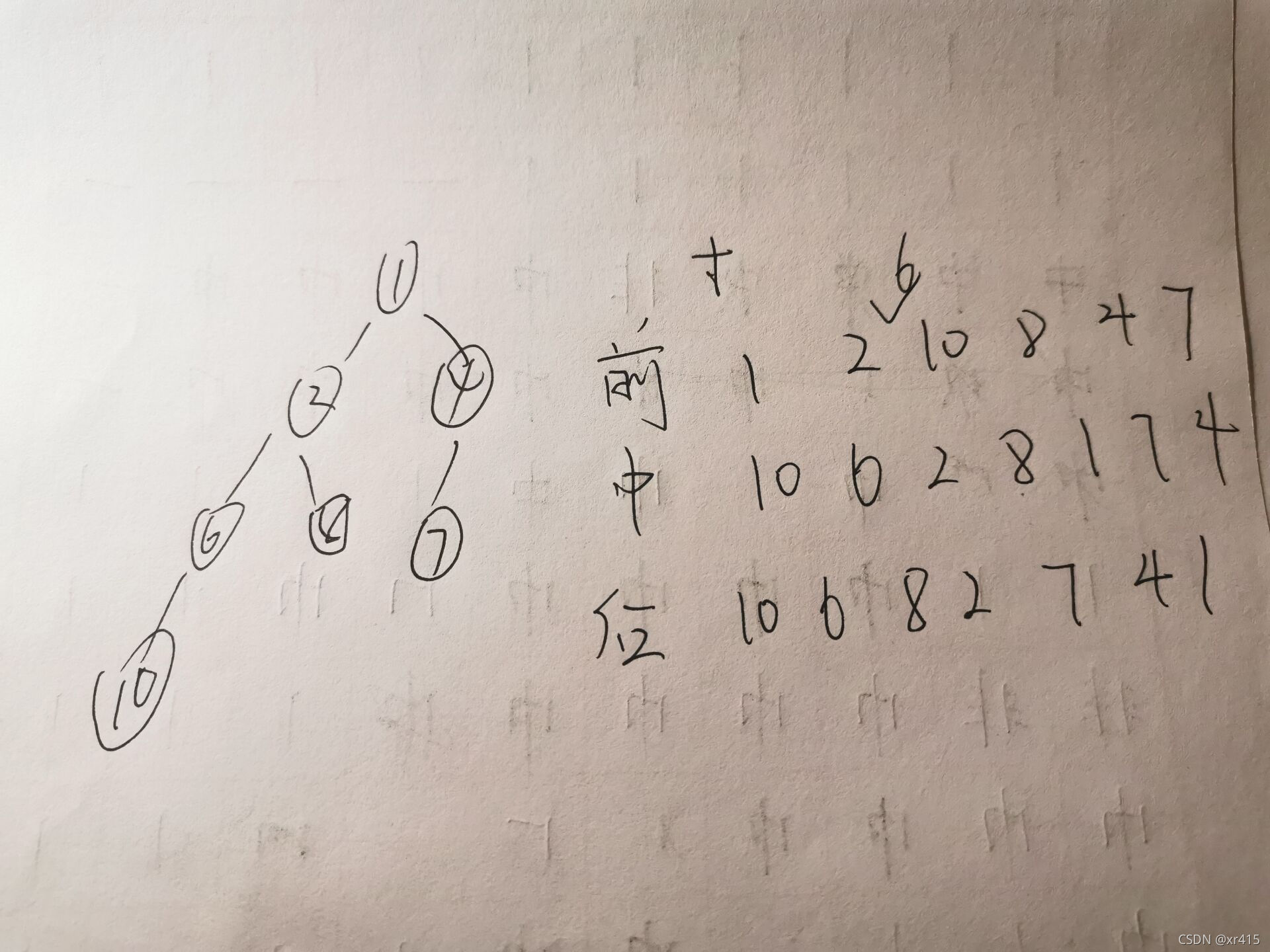
我们明确 只有先序中序或者后序中序能构建二叉树出来而先序和后序是构建不出来的

思路：

1.首先将先序中序的数字输入二个数组当中去

2.在中序遍历的数组中找到根节点记录下来，根节点

左边就是左子树，右节点就是右子树。

3.用递归去调用生成左子树和右子树

中序后序构建二叉树:

typedef struct node
{
	 int data;
	struct node* Lchild;
	struct node* Rchild;
	
}Node,*LPNode;
int mi[50];
int later[50];
LPNode creattree(int root, int start, int end)
{
	if (start > end)return NULL;
	LPNode tree = new Node;
	int i;
	tree->data = later[root];
	for (i = start; later[root] != mi[i]; i++);
	tree->Lchild = creattree(root-(end-i)-1, start, i - 1);
	tree->Rchild = creattree(root - 1, i + 1, end);
	return tree;
}
//有中序后序去构建树

构建树完成后我们进行代码测试：

int main()
{
	int n;
	cin >> n;
	LPNode root;
	cout << "输入中序" << endl;
	for (int i = 0; i < n; i++)
	{
		cin >> mi[i];
	}
	cout << "输入后序" << endl;
	for (int i = 0; i < n; i++)
	{
		cin >> later[i];
	}
	root = creattree(n-1, 0, n - 1);
	minorder(root);
	cout << endl;
	lastorder(root);
	return 0;
}

先序中序构建二叉树

typedef struct node
{
	 int data;
	struct node* Lchild;
	struct node* Rchild;
	
}Node,*LPNode;
int mi[50];
int later[50];

LPNode creattree1(int root, int start, int end)
{
	if (start > end)
	{
		return NULL;
	}
	LPNode tree = new Node;
	
	int i;
	for ( i = start; later[root]!=mi[i]; i++);
	tree->data = later[root];
	tree->Lchild = creattree1(root + 1, start, i - 1);
	tree->Rchild = creattree1(root+(i-start)+1 , i+ 1, end);
	return tree;
}
//说明这里的later[50]是存储先序结果的数组

这里的later[50]数组是存放先序遍历的结果的

int main()
{
	int n;
	cin >> n;
	LPNode root;
	cout << "输入中序" << endl;
	for (int i = 0; i < n; i++)
	{
		cin >> mi[i];
	}
	cout << "先序后序" << endl;
	for (int i = 0; i < n; i++)
	{
		cin >> later[i];
	}
	root = creattree1(0, 0, n - 1);
	minorder(root);
	cout << endl;
	lastorder(root);
	return 0;
}

结果演示:

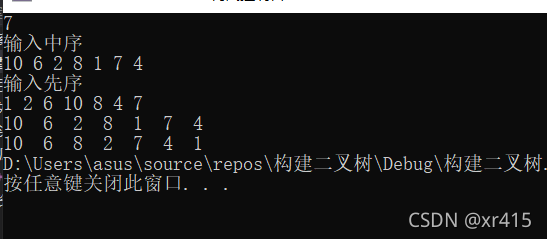
 2.先序中序后序递归遍历树:

先序遍历

void preorder(LPNode& root)
{
	if (root == NULL)
	{
		return;
	}
	cout << root->data << "  ";
	preorder(root->Lchild);
	preorder(root->Rchild);
}

中序遍历：

void minorder(LPNode &root)
{
	if (root == NULL)
	{
		return;
	}
	minorder(root->Lchild);
	cout << root->data << "  ";
	minorder(root->Rchild);
}

后序遍历：

void lastorder(LPNode& root)
{
	if (root == NULL)
	{
		return;
	}
	else
	{
		lastorder(root->Lchild);
		lastorder(root->Rchild);
		cout << root->data << "  ";
	}
}

总结：先序是先打印在调用左右孩子

           中序是先调用左孩子在打印在调用右孩子

           后序是先调用左右孩子在打印

 3.树的层次遍历

思路：

先入一个然后在出去后判断左右孩子是否存在 存在入队列

然后依次这样出去一个判断左右孩子是否存在知道队列为空就结束层次遍历

void level(LPNode& root)
{
	int front = -1;
	int rear = 0;
	LPNode queue[50];
	queue[rear] = root;
	while (front != rear)
	{
		
		front++;
		cout << queue[front]->data << "  ";
		if (queue[front]->Lchild != NULL)
		{
			rear++;
			queue[rear] = queue[front]->Lchild;
		}
		if (queue[front]->Rchild != NULL)
		{
			rear++;
			queue[rear] = queue[front]->Rchild;
		}

	}
}

4.判断树的高度和深度:

树的高度就是叶子节点开始计算

树的深度就是根节点开始计算

求树的高度思路：递归去实现当到叶子节点的时候就返回0，然后由于+1的操作会使叶子节点没上面一个节点都一直处于+1+1这样不断向升

typedef struct treenode
{
	int height;//每一个对应高度
	int data;
	struct treenode* Lchild ;
	struct treenode* Rchild;
}TNode,*PTRnode;

int SetHeight(PTRnode& root)
{
	if (root == NULL)
	{
		return 0;
	}
	else
	{
		root->height= max(SetHeight(root->Lchild), SetHeight(root->Rchild)) + 1;
		return root->height;
	}
}

求树的深度思路：用深度搜索的方式去一个一个遍历下去,函数有0一直+1+1的对每一个节点的深度进行赋值,这样每一个节点的深度就会改变，因为是先赋值在递归的。（先把左子树所有深度递归在进行右边所有子树递归

）

int setdepth(PTRnode& root,int depth)
{
	if (root == NULL)
	{
		return 0;
	}
	root->depth = depth;
	setdepth(root->Lchild, depth + 1);
	setdepth(root->Rchild, depth + 1);
}

5.树的销毁

思路：就是対树进行递归知道他左边孩子右边孩子都没有就释放这个节点

void destroytree(PTRnode& root)
{
	if (root == NULL)
	{
		return;
	}
	destroytree(root->Lchild);
	destroytree(root->Rchild);
	free(root);
}