二分查找 -leetcode-74. 搜索二维矩阵

最新推荐文章于 2024-06-15 12:03:32 发布

原创最新推荐文章于 2024-06-15 12:03:32 发布 · 668 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #二分查找

leetcode 专栏收录该内容

77 篇文章

订阅专栏

本文详细介绍了如何高效地在二维矩阵中搜索目标值，包括暴力、二分查找和BST三种方法。针对74.搜索二维矩阵问题，二分查找解法分为逐行查找和两次二分查找，时间复杂度优化至O(logm+logn)。而对于240.搜索二维矩阵II，解法主要为逐行二分查找，时间复杂度为O(m+n)。

74. 搜索二维矩阵

题目描述

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

暴力

暴力：一个一个元素找

时间复杂度 $O(n^2)$

二分查找

二分查找-解法1

逐行进行二分查找

时间复杂度： $O (m l o g n)$
空间复杂度： $O (1)$

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        for (int i = 0; i < matrix.length; i++) {
            if (binarySearch(matrix[i], target) != -1) {
                return true;
            }
        }
        return false;
    }

    public int binarySearch(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        System.out.println("right = " + right);
        while (left <= right) {
            int mid = left + (right - left) / 2;
            System.out.println("mid = " + mid);
            if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                return mid;
            }
        }
        return -1;
    }
}

二分查找-解法2：

由于本题说了，每行的第一个整数大于前一行的最后一个整数。 所以，查找 “行” 的操作，也可以使用二分查找

分 2 次进行二分查找：

第一次使用二分查找，找到所在 行；
不变量原则：找到最后一个满足 martix[i][0] <= target 的行号，最终即为 right 对应的行号 🔥

注意：当 right == -1 时，则说明 target < matrix[0][0]，此时 matrix 中肯定不存在 target。此时，需要单独处理，防止数组越界。 ⭐️
对 “行” 所有列，再进行一次二分查找

时间复杂度： $O (l o g m + l o g n)$
空间复杂度： $O (1)$

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        // 1、第一次二分：找 行
        // 找到最后一个满足 martix[i][0] <= target 的行号，最终 即为 right 对应的行号
        int left = 0;
        int right = matrix.length - 1;
        while (left <= right) { 
            int mid = left + (right - left) / 2;
            if (matrix[mid][0] > target) {
                right = mid - 1;
            } else if (matrix[mid][0] < target) {
                left = mid + 1;
            } else {
                right = mid;
                break;
            }
        }
        System.out.println("left = " + left);
        System.out.println("right = " + right);
        // 没有找到满足条件的行，即 right < 0（right = -1）时，则说明 target < matrix[0][0]，此时 matrix 中肯定不存在 target。
        if (right < 0) return false;
        // 当 “行” 的第一个元素就是 target 时，则不必再进行第二次 二分查找
        if (matrix[right][0] == target) return true;
        // 2、第二次 二分：找列
        System.out.println(binarySearch(matrix[right], target));
        return binarySearch(matrix[right], target) != -1;
    }

    public int binarySearch(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                return mid;
            }
        }
        return -1;
    }
}

BST

可以把整个矩阵看成一颗 以右上角元素为 root 的 BST：

如果 $当前元素 > t a r g e t$ ，则查找 “左子树” （即，左边列）
如果 $当前元素 < t a r g e t$ ，则查找 “右子树” （即，下边行）
如果 $当前元素 = = t a r g e t$ ，则 ok

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int c = matrix[0].length - 1;
        int r = 0;
        while (c >= 0 && r < matrix.length) {
            if (matrix[r][c] > target) {
                c--;
            } else if (matrix[r][c] < target) {
                r++;
            } else {
                return true;
            }
        }
        return false;
    }
}

时间复杂度： $O (m + n)$
空间复杂度： $O (1)$

240. 搜索二维矩阵 II

题目描述

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

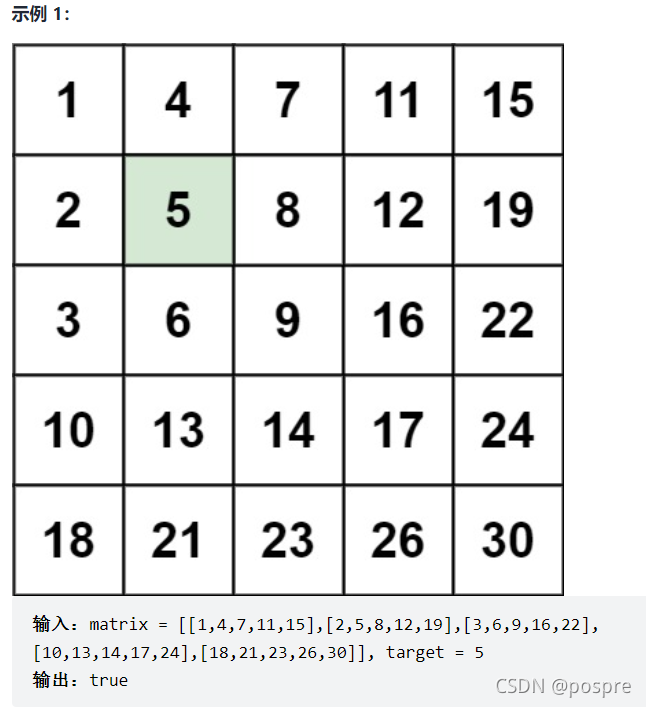
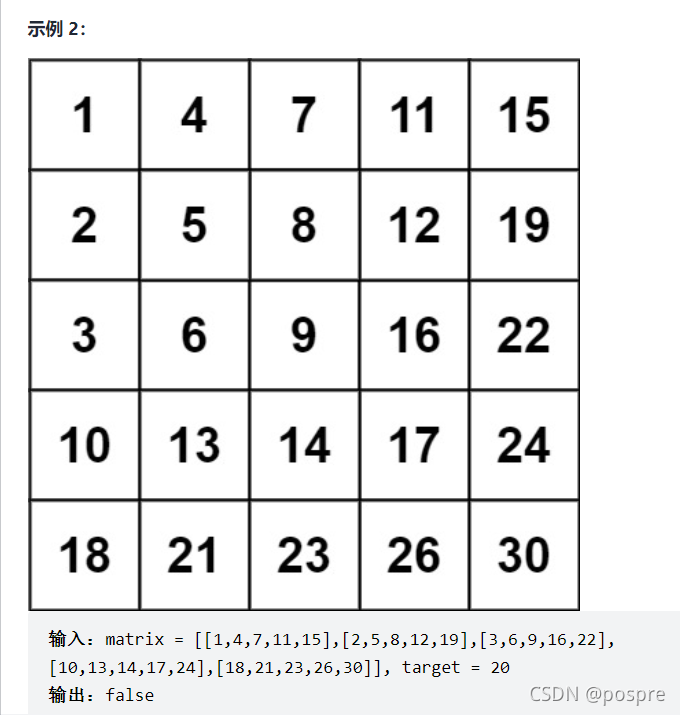
在这里插入图片描述
解法选择：

暴力：一个一个元素找，时间复杂度 $O(n^2)$
二分查找
BST （和 74. 搜索二维矩阵一样）

这里说下，本题大致和 74. 搜索二维矩阵一样。
但是，二分查找解法略有不同。
这里只讲二分查找注意事项

二分查找

由于 74. 搜索二维矩阵，每行的第一个整数大于前一行的最后一个整数。 所以，才可以分 2 次二分查找，分别找 “行” 和 “列”。

但是，本题 每列的元素从上到下升序排列。所以，只能分别对每行进行二分查找，不能用二分查找 “行”。

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int r = 0;
        int c = matrix[0].length - 1;
        while (r < m && c >= 0) {
            if (matrix[r][c] > target) { // 向左
                c--;
            } else if (matrix[r][c] < target) { // 向右
                r++;
            } else {
                return true;
            }
        }
        return false;
    }
}