临接列表的遍历

图

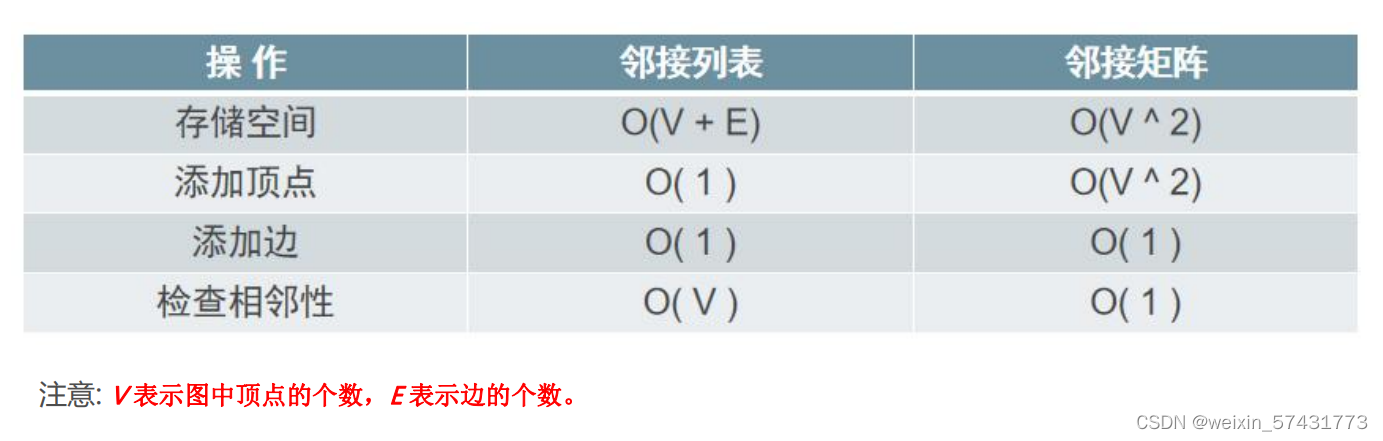
实现图的结构有两种，分别为邻接列表和邻接矩阵。我们着重研究的是邻接列表。

邻接列表

在邻接列表实现中，每一个顶点会存储一个从它这里开始的相邻边的列表

邻接列表的实现

#pragma once
#define MAX_SIZE 100
struct Edge {
	int weight;
	int adjnode;//相邻结点
	Edge* next;//下一条边
};
struct Node {
	char data;
	Edge* first;//指向第一条边
};
struct Map {
	Node* map;
	int nodeCount;
	int edgeCount;
};
void initMap(Map& m);
void createMap(Map& m);
int location(Map& m, char c);//将字符坐标转换为数字坐标
void DFS(Map& m, int v);//深度遍历
void DFS_Main(Map& m);
void DFS2(Map& m, int v);

#include <iostream>
#include <queue>
#include "Map.h"
bool visited[MAX_SIZE];
void initMap(Map& m) {
	m.map = new Node[MAX_SIZE];
	m.nodeCount = m.edgeCount = 0;
	for (int i = 0; i != MAX_SIZE; ++i) {
		visited[i] = false;	
	}
}
void createMap(Map& m) {
	printf("请输入顶点数和边数:");
	std::cin >> m.nodeCount >> m.edgeCount;
	printf("请输入结点的数据:");
	for (int i = 0; i != m.nodeCount; ++i) {
		std::cin >> m.map[i].data;
		m.map[i].first = NULL;
	}
	int weight;//权
	int i1 = 0;//数据坐标
	int i2 = 0;
	char c1, c2;//保存顶点的字符
	printf("请输入相关的边及其权值:");
	for (int i = 0; i != m.edgeCount; ++i) {
		std::cin >> c1 >> c2>>weight;
		i1 = location(m, c1);
		i2 = location(m, c2);
		if (i1 != -1 && i2 != -1) {
			Edge* edge = new Edge;
			edge->adjnode = i2;
			edge->weight = weight;
			//头插法
			edge->next = m.map[i1].first;
			m.map[i1].first = edge;
		}
	}
}
int location(Map& m, char c) {
	for (int i = 0; i != m.nodeCount; ++i) {
		if (m.map[i].data == c) {
			return i;//返回对应的下标
		}
	}
	return -1;
}
void DFS(Map& m, int v) {
	if (visited[v])return;//已被访问
	int next = -1;
	printf("%c\t", m.map[v].data);
	visited[v] = true;
	Edge* tmp = m.map[v].first;
	while (tmp) {
		next = tmp->adjnode;
		tmp = tmp->next;
		if (visited[next] == false) {
			DFS(m, next);
		}
	}
}
void DFS_Main(Map& m) {
	for (int i = 0; i != m.nodeCount; ++i) {
		if (visited[i] == false) {
			DFS2(m, i);
		}
	}
	std::cout << '\n';
}
void DFS2(Map& m, int v) {
	std::queue<int> Q;
	int cur, next;
	Q.push(v);//将第一个结点入队列
	while (!Q.empty()) {
		cur = Q.front();
		if (visited[cur] == false) {
			printf("%c\t", m.map[cur].data);
			visited[cur] = true;
		}
		Q.pop();
		Edge* tmp = m.map[cur].first;
		while (tmp) {
			next = tmp->adjnode;
			tmp = tmp->next;
			if (visited[next] == false) {
				Q.push(next);//将当前结点的所有相邻结点入队
			}   
		}
	}
}

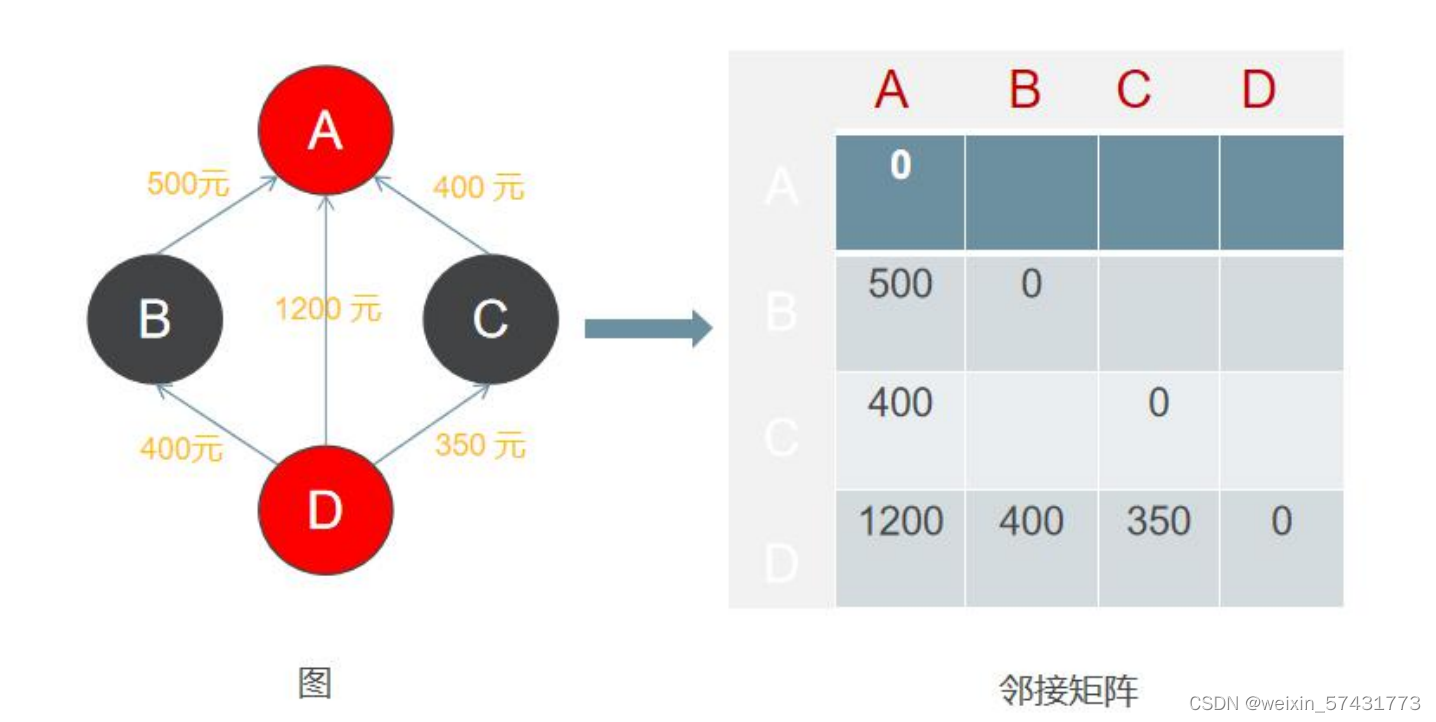
邻接矩阵

由二维数组对应的行和列都表示顶点，由两个顶点所决定的矩阵对应元素数值表示这里两个顶点是否相连（如， 0 表示不相连，非 0 表示相连和权值）、如果相连这个值表示的是相连边的权重。例如，广西到北京的机票， 我们用邻接矩阵表示

注意事项

大多数情况下，选择邻接列表都是正确的，尤其是在图比较稀疏的时候。因为邻接矩阵无论是在建立的时候还是在添加结点的时候，它的时间复杂度都比较高。除非是当图特别密集的时候，我们才需要考虑一下邻接矩阵。

最短路径-(了解即可)

int min_weight = 0x7FFFFFFF;//最小权
int step = 0;
int path[MAX_SIZE] = { 0 };
int shortest_path[MAX_SIZE] = { 0 };
void shortest_DFS(Map& m, int begin, int end, int weight) {
	int cur = begin;
	if (cur == end) {
		for (int i = 0; i != step; ++i) {//输出每条可能路径
			std::cout << m.map[path[i]].data << '\t';
		}
		printf("\n对应的权值为:%d\n", weight);
		if (weight < min_weight) {
			min_weight = weight;
			memcpy(shortest_path, path, sizeof(int) * step);
		}
	}
	visited[begin] = true;
	Edge* tmp = m.map[cur].first;//拿到第一条边
	while (tmp) {
		int tmp_weight = tmp->weight;
		cur = tmp->adjnode;
		if (visited[cur] == false) {
			visited[cur] = true;
			path[step++] = cur;//保存路径
			shortest_DFS(m, cur, end, weight + tmp_weight);
			visited[cur] = false;//前一步探索完毕,要回溯
			path[--step] = 0;
		}
		tmp = tmp->next;
	}
}