算法训练11.6

 简单的打卡题，直接随便搞一下

class Solution {
    public String interpret(String command) {
        String res="";
        for(int i=0;i<command.length();){
            if(command.charAt(i)=='('){
                if(command.charAt(i+1)==')'){
                    res+="o";
                    i+=2;
                }
                else{
                    res+="al";
                    i+=4;
                }

            }
            else{
                res+="G";
                i++;
            }
        }
        return res;
    }
}

顺便学个api的方法

class Solution {
    public String interpret(String command) {
        return command.replace("()","o").replace("(al)","al");
    }
}

---

 每个数，要么是他是原来的数，要么他就是原来的数的倍数，那么第一想法就是排列，这样从小找到大，就可以确定最小的数一定不是倍数，因为他是最小的，包括0，如果有0就应该存在两个0，所以完全可以把第一个0当原来的数，例如 1 2 3 4 6 8 ，排列以后，1消了2,3消了6,4消了8，那为什么不怕2和4需要配对，因为最小的1不可能是倍数了，必须先满足找他的倍数，不然就一定不成立。按上述方法的写法

class Solution {
    public int[] findOriginalArray(int[] changed) {
        ArrayList<Integer> list=new ArrayList<>();
        Arrays.sort(changed);
        int n=changed.length;
        if(n%2==1) return new int[]{};
        int[] arr=new int[n/2];
        int index=0;
        for(int i=0;i<n;i++){
            list.add(changed[i]);
        } 
        for(int i=0;i<n/2;i++){
            int a=list.get(0);
            list.remove(0);
            if(list.contains(2*a)){
                arr[index++]=a;
                list.remove((Integer)(2*a));
            }
            else
            return new int[]{};
        }
        return arr;
    }
}

用到了集合，每次查找，删除都需要时间，显然复杂度会过高，那么考虑用散列，保存每个数字的个数，排列以后拿出一个来，这个数字个数减1，他的倍数个数减1，如果他的倍数个数小于0，那么就不成立，而且应该先判断当前数还有没有，例如1 2 3 4 6 8，1把2用了，到2时没了，应该直接跳去3

class Solution {
    public int[] findOriginalArray(int[] changed) {
        int[] num=new int[1000001];//题目是0 <= changed[i] <= 105，但是却存在200000，所以直接多用点
        for(int i=0;i<changed.length;i++){
            num[changed[i]]++;//记录每个数字个数
        }
        Arrays.sort(changed);//将数组排列
        if(changed.length%2==1){//数组长度为奇数一定不能构成
            return new int[]{};
        }
        int[] res=new int[changed.length/2];//保存结果
        int index=0;
        for(int i=0;index<changed.length/2;i++){
            if(num[changed[i]]<=0){//当前数已经被用了
                continue;
            }
            num[changed[i]]--;
            num[changed[i]*2]--;//个数减1
            res[index++]=changed[i];
            if(num[changed[i]*2]<0)//不存在倍数，返回
            return new int[]{};
        }
        return res;
    }
}

---

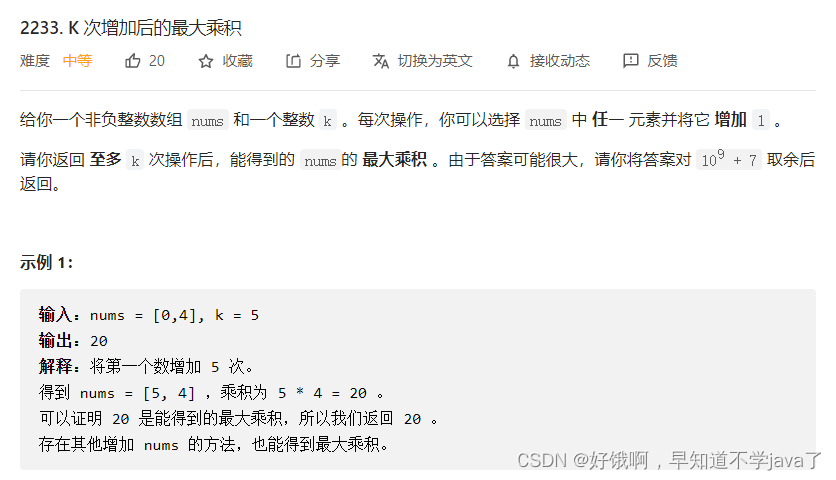先来应该百分百超时的方法，题目需要的就是每次把最小的数加1，为什么？1,4中，给1加1结果就是加了一个4，而给4加1结果只加了一个1，同理，1,2,4，给1加1就是加了一个2*4，给4就是加了一个1*2，所以要每次给最小的数加1，大概思想是这样的，像下面的写法，但是一定是超时的

class Solution {
    private static final int mod=1000000007;
    public int maximumProduct(int[] nums, int k) {
         
        while(k>0){
            int min=Integer.MAX_VALUE;
            int index=0;
            for(int i=0;i<nums.length;i++){
                if(nums[i]<min){
                min=nums[i];
                index=i;}
            }
            nums[index]++;
            k--;
        }
        long res=1;
        for(int i=0;i<nums.length;i++){
            res=(res*nums[i])%mod;
        }
        return (int)(res%mod);
    }
}

思想大概是这样，但是每次这样查找最小值是不可能的，时间复杂度达到了n的k次方，显然是不可能的，这种维护最小值的问题，脑子里出现一个单调栈和一个优先队列，太久没写过单调栈的问题了，也不知道是不是用于这种问题，这里选择使用api的优先队列。

class Solution {
    private static final int mod=1000000007;
    public int maximumProduct(int[] nums, int k) {
        Queue<Integer> queue=new PriorityQueue<>();
        for(int i:nums){
            queue.offer(i);
        }
        while(k>0){
            int num=queue.poll();
            num++;
            queue.offer(num);
            k--;
        }
        long res=1;
        while(!queue.isEmpty()){
            res=(res*queue.poll())%mod;
        }
        return (int)res;
    }
}

附上一个以前写过的单调栈的经典问题，找到一个数组中左右两边元素比当前位置小的最近位置

例如：arr=3,4,1,5,6,2,7

那么位置为0也就是3时就是[-1,2]，位置为1也就是4时就是[0,2]。。。

这个问题就需要使用单调栈，维护一个递减的单调栈，到第一个位置就是3时，把位置压入栈中，然后到4时，4大于栈顶位置的元素3，继续把位置压入栈，到1时，1小于4，弹出4的位置，比4小右边的最近元素就是1，左边就看栈顶的元素（因为维护了栈的单调性），也就是3，那么4就是[0,2]，1还小于3，弹出3，右边比3小还离他最近的元素也是1，左边看栈顶，没了，就是-1，继续压入1，以此类推

import java.util.Arrays;
import java.util.Stack;

public class 单调栈 {
    //找到数组中i位置左右两边比他小的最近位置
    public static void main(String[] args) {
        int[] arr={3,4,1,5,6,2,7};
        int[][] res=getNearLessNoRepeat(arr);
        System.out.println(Arrays.deepToString(res));
    }
    public static int[][] getNearLessNoRepeat(int[] arr){
        int[][] res=new int[arr.length][2];
        Stack<Integer> stack=new Stack<>();
        for(int i=0;i< arr.length;i++){
            while(!stack.isEmpty()&&arr[i]<arr[stack.peek()]){//当前位置小于栈顶元素位置，需要维护栈是单调递减的
                int popindex=stack.pop();
                int leftlessindex=stack.isEmpty()?-1:stack.peek();
                res[popindex][0]=leftlessindex;
                res[popindex][1]=i;
            }
            stack.push(i);
        }
        while (!stack.isEmpty()){//对剩余元素清算
            int popindex=stack.pop();
            int leftindex=stack.isEmpty()?-1:stack.peek();
            res[popindex][0]=leftindex;
            res[popindex][1]=-1;
        }
        return res;
    }
}