GRP-HEFT：A Budget-Constrained Resource Provisioning Scheme for Workﬂow Scheduling in IaaS Clouds-CSDN博客

本文链接：https://blog.csdn.net/weixin_58628068/article/details/145899101

摘要

针对IaaS云中完工时间过高，提出了Greedy Resource Provisioning and modiﬁed HEFT (GRP-HEFT)，根据实例类型的效率比率对它们进行排序。

简介

在云中，要尽可能使用更短的执行时间运行他们的应用程序，要平衡预算，速度，工作负载等因素。

在预算内找到最快工作流是要解决的问题，即异构最早完成时间HEFT。

基于基本成本模型不太有希望，开始向基于小时的成本模型改变。

本文目的：目标函数是最小化给定工作流的完成时间(makespan)，用于基于小时的成本模型。包括资源分配算法和调度算法。资源分配算法是从指定云提供商提供的无线资源池中获取多少和哪种类型的实例，调度程序确定将任务分配给获得的实例以及每个实例内任务的执行顺序。

选了三个算法与GRP-HEFT比较，分别是PSO（一种基于粒子群优化算法的单目标优化方法，该方法在预算限制下使完工时间最小化）、GA（一种基于遗传算法的单目标、受截止时间限制的工作流调度算法，该算法使工作流的执行成本最小化）和MOACS（一种多目标即成本与完工时间的优化方法）

问题描述

三个维度来考虑算法，一是在特定预算下选取一定实例来运行工作流，二是将任务调度到选定的实例集上，三是执行顺序在上面举得三个例子中，基于小时的成本模型可能会导致超出预算，且一定是比基于成本的模型消费要高，此外，在例3中，基于成本模型并没有考虑到任务3所带来的一个小时的花费。

问题建模

一个工作流由DAG表示，T表示任务集合，E表示任务依赖之间集合，CR是任务之间传输数据大小。

云资源池共M=N*m个实例，N是任务数，m为实例类型数

e表示任务T在实例类型p上执行的时间，比较的是同一任务在不同实例下运行的时间，也可以使用计算单元CU或类似指标量化实例处理能力，CU是实例类型p的CU值，越高表示计算能力越强

任务执行时间e计算为，其中ref_time是参考执行时间，即CU=1的实例上任务的执行时间。

此外还涉及到通信时间，使用的是最小带宽。

使用分配x表示一种解决方案（所有可能的组合（i）在实例池中选择云实例的一个子集，（ii）将任务分配给所选实例子集的不同方式，以及（iii）任务执行顺序的各种排列，构成了问题空间。）

1.任务到实例的分配表示为一个包含N个任务的向量X，任意一个任务可能用任意一个实例类型，当X数组的第i个元素为j时，表示第i个任务被分配到第j个实例。

2.为了表示每个实例的类型，用一个包含M个元素的向量Y，当Y数组的第j个元素为k时，表示第j个实例的类型是k。为了降低复杂度，Y的元素数量可以减少到已使用实例的数量，而不是M。

3.用一个包含N个元素的向量Z表示任务的执行顺序，每个元素是一个介于1到N之间的整数值。Z数组元素的顺序应该符合有向无环图（DAG）的拓扑排序。其中第一行是顺序，第二行才是任务序号。

执行整个工作流的所需总时间即完工时间为

其中k表示任务tp的实例，j表示任务ti的实例，BWkj表示实例k和j的带宽。tp是在ti前，CPUAvailableTimej表示第j个实例的CPU可用时间。即第j个实例的CPU最早可用于执行ti的时间。

完成时间为

总时间为

优化问题的构建

最小化工作流的完成时间Makespan(x)，约束条件为“总成本函数TotalCost(x)不超过预算Budget.

共两种模型，基于小时成本和基于每秒成本模型，只考虑亚马逊EC2提供的基于小时的计算模型。此外网路成本视为零，则总花费如下：

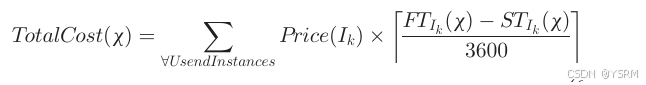
集合UsedInstances是根据分配x至少被分配了一个任务的所有实例的一个子集，FT表示第k个实例的完成时间，ST表示第k个实例的开始时间，单位为s，所以除以3600。

问题框架

GRP-HEFT算法

资源供应策略

确定应该使用哪些实例类型以及每种实例类型应该选取多少个。先检查支配性，即高价低能的要被低价高能的支配，优先考虑具有支配权的实例类型，对于不会被支配的实例类型即最好的优先添加到InstTypeList的列表中，如果效率即性价比相同，优先选CU高的，更适合工作流的调度，效率计算如下：

把预算尽可能用来购买InstTypeList里最好的实力类型，直到钱不够，以此类推，直到最便宜的(Pricecheapest)都买不了，得到实例集Y。

接着Y和DAG作为改进HEFT的输入，得到X和Z，在不断循环中，得到最优x，然后从InstTypeList中移除效率最高的实例类型（可能找到其他更优结果），再进入下一次迭代，直到列表为空。

改进的HEFT算法

资源调度策略

和HEFT区别主要在于，一旦实例的执行时间超过整个小时数就会尝试BVA（避免预算违规）。

首先在排序阶段采用向上排名度量确定执行顺序，通过尽早执行具有更多依赖关系的任务、确定顺序后就开始将任务分配给资源。对于每个任务初始化，最小化的实例，最优最小化的实例，最小化的完成时间，最优最小化的完成时间，接着从Y中遍历每个实例，计算该任务在该实例下的完成时间，如果更快，则更新最小化的实例和时间，如果将该任务添加到该实例，没有超过整个小时，即不会造成成本增加，更新最优最小化实例和最优最小化时间。

在确定完这些后到17-19的BVA机制，如果最小化和最优最小化不相同（最小化会造成成本增加），且如果有和最小化实例类型相同的且未被使用的实例，从Y中移除，再次利用最小化示例，减少更改实例带来的成本增加，避免预算超出，例子如下，1个Instance1和1个Instance2被替换为2个Instance1。