闫氏DP分析法 --- 01背包、完全背包

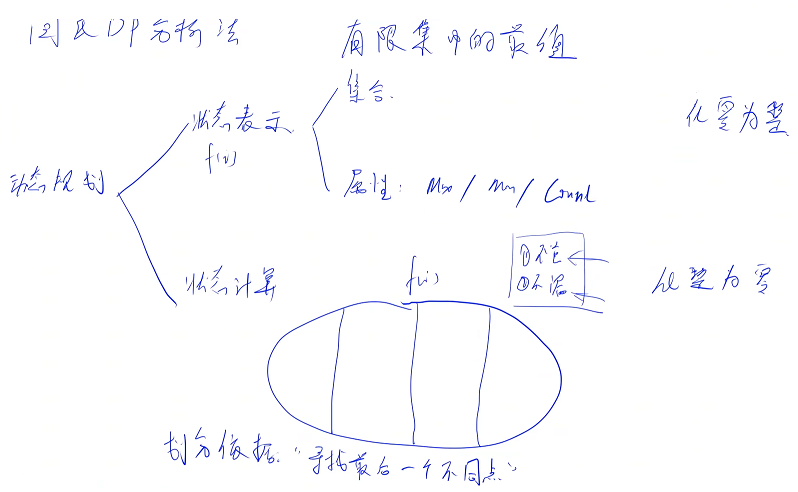
核心是从集合角度来分析 dp 问题

所有的 dp 问题都是有限集中的最优化问题(给出一个集合求元素最值或者数量或者是否存在），集合中的元素数量一般为指数级别，如果想把每种方案都枚举一遍，时间复杂度太高，因此就可以用 dp 来优化

分析 dp 问题一般需要经过两个阶段，第一个阶段化 0 为整，每次处理问题不是一个一个元素去枚举，而是每次枚举一个子集（一类有相似点的元素），用某一个状态来表示

f[ i ] 表示的是哪个集合（所有满足某个条件的方案的集合），每次可以表示一类东西，而不是一个东西，从而可以优化时间复杂度，f[ i ] 表示的是一个集合，但是存储的是一个数字，这个数和集合的关系称为属性 max、min、count

第二个阶段状态计算，化整为 0，先看一下 f[ i ] 表示的所有状态是什么，把 f[ i ] 化分为若干个不同的子集每个部分分别求 f[ i ]，这些子集一般要满足两个原则：①不重复(求数量时，要保证不重复，每一个元素只属于其中的一个集合【求最大值，可以重复：求 A、B、C 集合的最大值可以先求 A、B 最大值，再求 B、C 最大值，最后取两段集合的最大值的 max，虽然 B 重复了，但是不影响最大值】，如果求数量必须不重复) ②不遗漏（所有子集中里面的元素一定把 f[ i ] 中的所有元素都包含了，不能漏掉某一个元素）

想求 f[ i ] 的时候就可以分别求每个子集所对应的值，整个集合的最大值就是每一个子集的最大值取 max

把整体问题划分为某些子集的问题，每一个子集都处理一下

集合划分的依据：一般找最后一个不同点

01 背包问题 

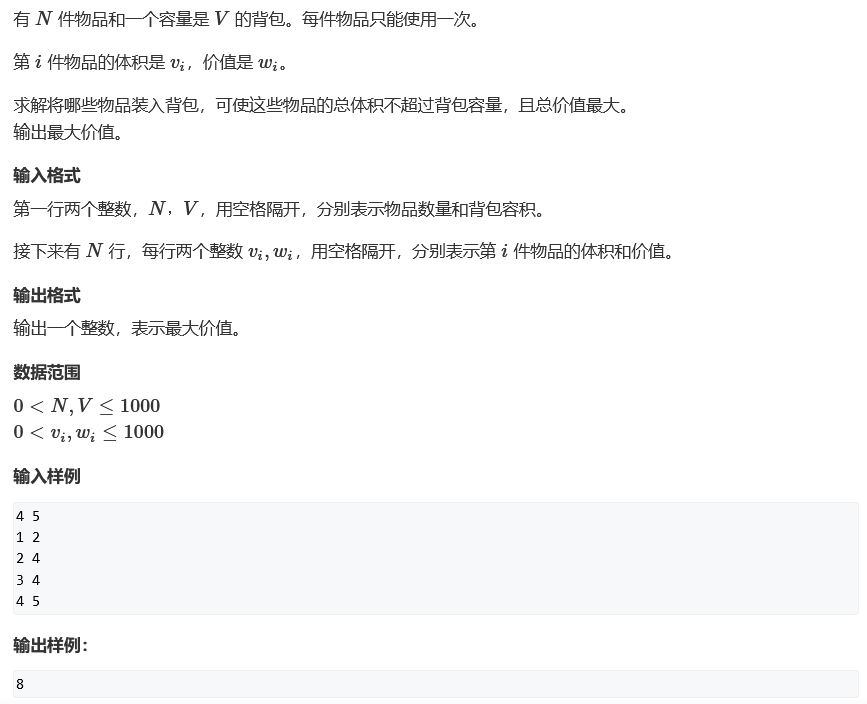
有 N 件物品和一个容量是 V 的背包，每个物品只能用 0 次或者 1 次，每个物品要么选要么不选，最多有两种情况，选法的数量最多为 2^n，从 2^n 的方案里面找出总价值最大的方案

第 i 个物品的体积是 vi 价值是 wi

有限集合求最值问题，物品数量有限 N，容量有限 v

给出每个物品的属性：①体积 ②价值

选择一些物品放入背包(选择方案的数量是有限的)，使得这些物品的总体积不超过背包容量 v，并且所有物品的总价值和最大，输出最大价值和是多少

第一个是物品个数，第二个是背包容量

接下来输入 n 行，每行输入物品的信息，第一个数是物品的体积，第二个数是物品的价值

暴力求解背包问题：枚举所有方案，对于每一个方案，判断总体积有没有超过 v，然后求最大值，更新最大值

二维动态规划

f[ i ][ j ]：第一维表示只看前 i 个物品，第二维选择物品的总体积是 j 的情况下（给出限制），总价值最大是多少（集合的描述：所有满足条件 1、条件 2 (对应到状态表示的每一维) 的元素的集合）

题目问的是什么：总价值最大是多少？ f[ i ][ j ] 存储的值就是什么：集合中每一个方案的最大价值（属性）

result = max{ f[ n ][0 ~ V] }

f[ N，V ] 就是所有只考虑前 N 个物品，且总体积不超过 V 的选法集合，f[ i ][ j ] 集合里面的最大值就是答案，也就是说

f[ N，V ] 就是答案

求 f[ i ][ j ] 所表示集合里面的最大值

先把 f[ i ][ j ] 划分成两个子集，这两个子集是没有重复的 ①不重复 ②不遗漏

属性是集合当中每一个方案的最大价值，集合当中的方案都是合法方案，从 i 个物品里面选，并且总体积不超过 j

找最后一个不同点 (选第 i 个物品和不选第 i 个物品是两种不同的方案)，把集合划分为两个子集，每一个子集要么包含第 i

个物品、要么不包含第 i 个物品

如果想求 f[ i ][ j ] 的最大值，只需要分别求出来左边子集的最大值和右边子集的最大值，两边取 max，就是 f[ i ][ j ] 的最大值

怎么求左边子集的最大值？从定义出发

左边子集在 f[ i ][ j ] 中，需要满足 f[ i ][ j ] 的限制：从 1 到 i 中选，且总体积小于等于 j，并且由于在左边，所以不包含物品 i，因此就是所有从 1 到 i - 1 中选，且总体积小于等于 j 的方案的集合，也就是 f[ i - 1 ][ j ]

怎么求右边子集的最大值？

所有包含第 i  个物品的方案，前面可以随便选，最后包含第 i 个物品，怎么求这种所有方案的最大值呢？只需要把所有方案分成两个部分，前面是变化的部分：如果想让整个最大 (不变的部分已经不能变了)，应该让变化的部分最大，后面是不变的部分都是 i：每一个部分都是包含物品 i，价值 wi，固定不变

变化的部分的最大是什么呢？

每一个方案是从 1 到 i 中选，必然包含 i，总体积小于等于 j，现在看变化的部分(不包含 i 的部分，把 i 去掉)：从 1 到 i - 1 中选，且总体积小于等于 j - vi 的方案的集合的最大值(加上物品 i 之后小于等于 j)，也就是 f[ i - 1 ][ j - vi ]

最终整个集合的最大值就是左子集的最大值和右子集的最大值取 max

注意：

划分的时候可以划分为两个集合，但是求的时候，右边的集合不一定存在

由于要求右边的集合必须包含物品 i，如果 j < vi，右边不可能包含物品 i， 当 j < vi，右边的集合就是空的，求的时候需要特判，只有 j ≥ vi，才应该计算右半部分

假设把前 i - 1 个物品的状态计算完了，现在看第 i 个物品，看第 i 个物品有哪些选择：

1.不选择第 i 个物品：f[ i ][ j ] = f[ i - 1][ j ](表示只考虑前 i - 1 个物品，体积是 j 的情况下的最大价值)

2.选第 i 个物品 f[ i ][ j ] = f[ i - 1][ j - v[ i ] ](需要从 j 里面把 i 的体积去掉) 当前剩下的可以装东西体积：j - v[ i ]，第 i

个物品已经考虑完了，只需要考虑前 i - 1 个物品即可

直接输出 f[ n ][ m ] 就好。f[ n ][ m ] 的含义参照集合的定义，因为 f[ n ][ m ] 表示的就是所有从 1 - n 中选，且总体积不超过 m 的方案的集合，f[ n ][ m ] 中存储的就是集合的最大值

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;
//物品个数 背包容量
int n,m;

int f[N][N];
//记录每个物品的体积和价值
int v[N],w[N];
int main()
{
    cin >> n >> m;
    for(int i = 1;i <= n; i++ ) cin >> v[i] >> w[i];
    //从前往后循环每一个物品
    for(int i = 1;i <= n;i++ )
        //从前往后枚举所有的体积
        for(int j = 0;j <= m;j++ )
        {
            //左边的最大值
            f[i][j] = f[i - 1][j];
            //右半边不一定存在
            if(j >= v[i])
                //右半边是所有包含第 i 个物品的方案-> 当前的总容量 j 可能小于第 i 个物品的体积-> j < v[i]
                //用右边更新f[i][j]
                f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + w[i]);
        }
    //输出最大值
    cout << f[n][m] << endl;
    return 0;
}

01 背包问题优化

从时间上不能再优化，只能优化空间复杂度，优化成一维

观察状态方程可以发现 所有f[ i ] 的状态在计算的过程中只会用到 f[ i - 1] 这一层 (每次计算只与前一层有关)，没必要把所有层都记录下来

 

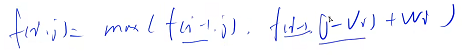
第二维的 j 要么是用到 j (自己)，要么是用到 j - vi（比自己小的数），只要保证 j 从大到小循环即可

用滚动数组优化，每次只需要保留上一层的结果即可，之前的结果不会再用到，所以可以删掉

dp 问题的所有优化都是对代码做等价变形，和问题本身没有关系，只与代码逻辑有关系

参考题解：

01背包问题（状态转移方程讲解）

01背包问题

动态规划DP

贪心算法逐步优化、解决背包问题

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;
//物品个数 背包容量
int n,m;

int f[N][N];
//记录每个物品的体积和价值
int v[N],w[N];
int main()
{
    cin >> n >> m;
    //读入每一个物品的体积和价值
    for(int i = 1;i <= n;i++ ) cin >> v[i] >> w[i];
    //从前往后循环每一个物品-> i 从 1 循环还是从 0 循环-> 考虑每一个状态是不是合法的-> f[i][0]
    //前 i 个物品,总体积是0-> 前 i 个物品可以都不选
    for(int i = 1;i <= n;i++ )
        //从前往后枚举所有的体积
        //for(int j = 0;j <= m;j++ )
        for(int j = m;/* j >= 0 */j >= v[i];j-- )
        { 
            f[j] = f[j];
            //f[i][j]是第i层的j 它右边的值还没有被更新过f[i - 1][j]-> 左右两边等价
            //f[i][j] = f[i - 1][j];-> 在计算f[j]的时候右边f[j]还没有被更新过 右边的值会被先计算出来再去更新左边这个值
            //需要保证后面是 i - 1-> 调整循环顺序为从大到小即可-> 保证在计算f[j]的时候j - v[i]比f[j]小
            //从大到小循环 先算f[j] 再算f[j-v[i]]-> 计算f[j]用到的就是上一层的f[j-v[i]]
            //f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + w[i]);
            f[j] = max(f[j],f[j - v[i]] + w[i]);
            //f[i][j]是第i层的j-> 从小到大枚举j-> j - v[i] 一定小于j-> 在计算f[j]之前,j - v[i]已经被计算出来了
            //此时 j - v[i] 是第 i 层的 j - v[i]
            //f[i][j] = max(f[i][j],f[i][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    return 0;
}

完全背包问题

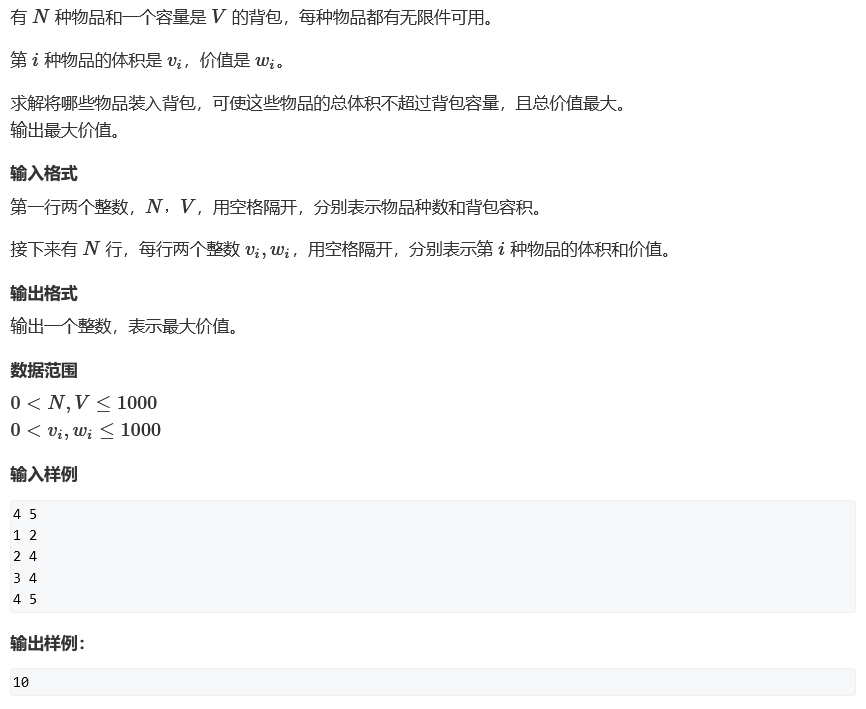
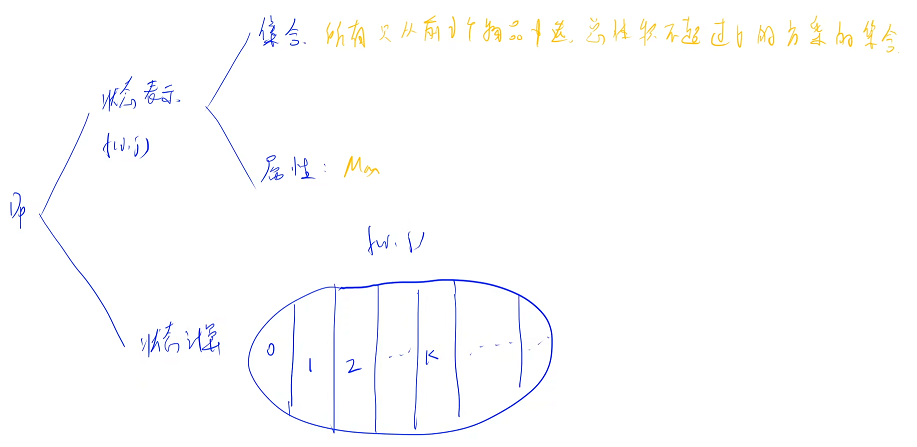
状态计算

完全背包问题：每一个物品可以用无限次：第 i 个物品可以选无限次，在枚举的时候需要划分为若干个子集(第 1 个子集不选第 i个物品，选 0 个第 i 个物品：从 1 到 i - 1 中选，且总体积小于等于 j 的方案的集合，最大值就是 f[ i - 1 ][ j ]；第 2 个子集选 1 个物品第 i 个物品. . .第 k 个子集选 k 个物品第 i 个物品)，直到选到不能选为止(体积超过 j 为止)，01 背包问题：每一个物品只能用一次(以第 i 个物品选还是不选分为两个集合)

如果想求最大值，需要把每一个子集都求出来取 max

每一个方案选择第 i 个物品的数量是确定的，不重不漏

考虑包含了 k 个第 i 个物品的所有方案，求这些方案的最大值

可以把每个方案分成两个独立的部分：前面是变化的部分（如果想要整个子集最大，就是求前面的最大值，从定义出发：从 1 到 i 中选，总体积小于等于 j，已经把 k 个 i 剔除了，不包含 i，相当于从 1 - i - 1 中选，加上 k 个 i 后，总体积不超过 j，如果不算这 k 个 i，总体积应该小于等于 j - k × vi），后面的不变的部分（后面是固定的）

从 1 - i - 1 中选，总体积小于等于 j - k × vi 的方案的集合，这个方案集合的最大值就是 f[ i - 1 ][ j - k × vi ]，最终的 f[ i ][ j ] 的最大值就是所有的集合取 max

01 背包问题有 2 项，完全背包问题有 n 项

如果暴力写，需要三重循环，n 是 1000，时间复杂度为 10^9，会超时，需要推导把完全背包变成两重循环

看中间的某个状态：f(i，j - v)，上面每一项比下面的每一项都多一个 w，其余完全一样，求上面的最大值就是下面的最大值加 w

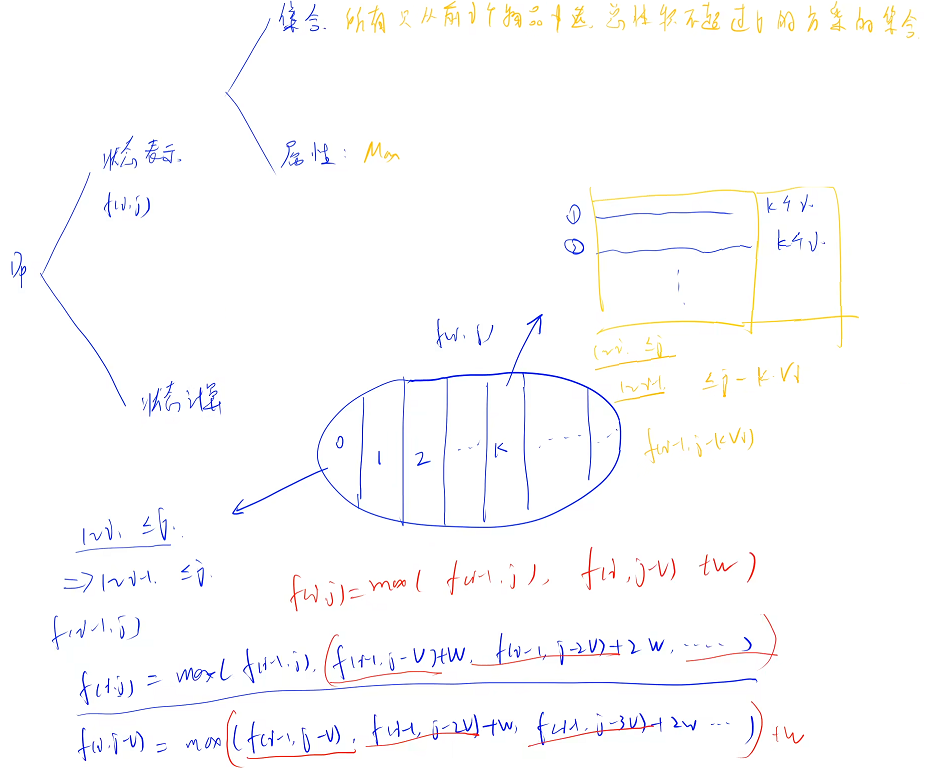
比较 01 背包 和 完全背包的状态方程：

   01 背包：f[ i ][ j ] = max( f[i - 1][ j ]，f[ i - 1 ][ j - v ] + w )

完全背包：f[ i ][ j ] = max[f[ i - 1][ j ]，f[ i ][ j - v ] + w )

如果优化空间的话，一个从小到大枚举体积，一个从大到小枚举体积；如果两维空间没有任何限制

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N =1010;
//物品个数 背包容量
int n,m;

int f[N][N];
//记录每个物品的体积和价值
int v[N],w[N];
int main()
{
    cin >> n >> m;
    for(int i = 1;i <= n;i++ ) cin >> v[i] >> w[i];

    //从前往后循环每一个物品-> 前i个物品可以都不选
    for(int i = 1;i <= n;i++ )
        //从前往后枚举所有的体积
        for(int j = 0;j <= m;j++ )
        {
            //左边的最大值
            f[i][j] = f[i - 1][j];
            //右半边集合不一定存在
            if(j >= v[i])
                //右半边至少包含一个物品i j可能小于第 i 个物品的体积 第 i 个物品一个都装不下
                f[i][j] = max(f[i][j],f[i][j - v[i]] + w[i]);
        } 
    //输出-> 从 n 个物品中选,总体积不超过 m 的方案集合的最大值
    cout << f[n][m] << endl;
    return 0;
}

优化空间后，未优化空间为 4340 kB，优化空间后为 368 kB

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N =1010;
//物品个数 背包容量
int n,m;

int f[N][N];
//记录每个物品的体积和价值
int v[N],w[N];
int main()
{
    cin >> n >> m;
    for(int i = 1;i <= n;i++ ) cin >> v[i] >> w[i];

    //从前往后循环每一个物品-> 前i个物品可以都不选
    for(int i = 1;i <= n;i++ )
        //从前往后枚举所有的体积
        for(int j /* = 0;j > */= v[i];j <= m;j++ )
        {
            //右边的 f[j] 此时存储的是上一层的f[j]-> f[j]还没有在第 i 层循环被更新过 第一个等式是等价的
            //f[i][j] = f[i - 1][j];
            //f[j] = f[j];
            //< v[i]的都会被跳过 直接从v[i]开始循环即可
            //if(j >= v[i])
            f[j] = max(f[j],f[j - v[i]] + w[i]);
            //f[i][j]是第i层的j 在算 f[j] 的时候,f[j - v[i]]已经被计算出来
            //此时的f[j - v[i]]就是第 i 层的 j - v[i] 完全等价
            //j 从小到大循环 v[i]大于0 j- v[i] < j
            //f[i][j] = max(f[i][j],f[i][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    return 0;
}