LeetCode 1496 - 1499

判断路径是否相交

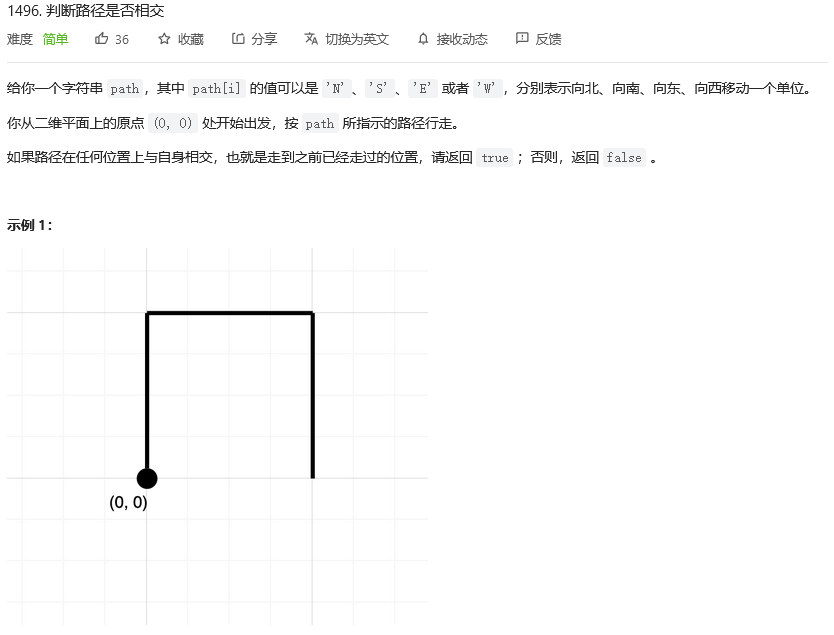
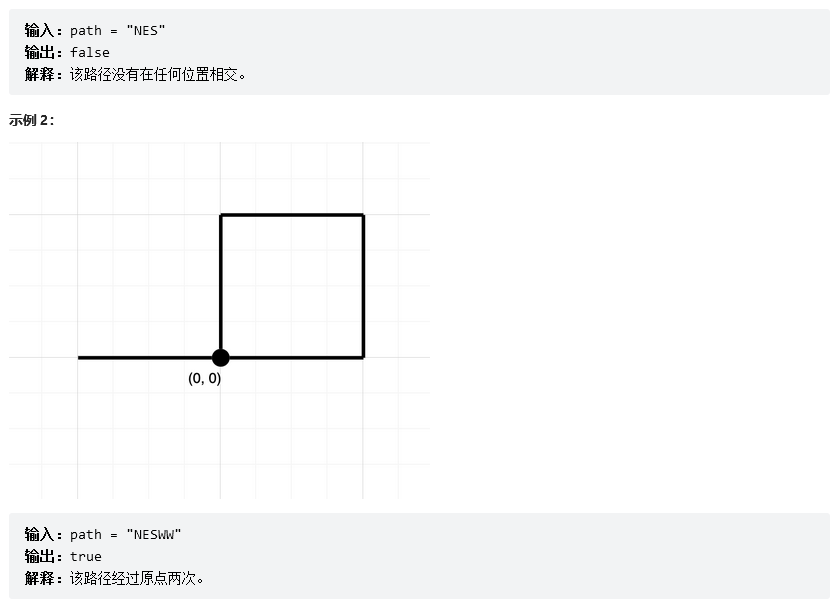
一开始原点有一个小人，给这个小人一堆指令，这些指令分别为 'N'、'S'、'D'、'W'（东南西北四个方向），对于每个指令会朝着四个方向中的某一个走 1 个单位的长度（此题左右互换无所谓，由于是对称的，答案是一样的）

示例 1：

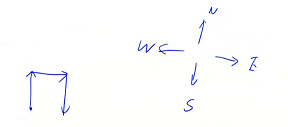
我们可以根据给出的指令走出一条路线，问：在走的过程中，有没有出现重复的点

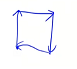
如果走的过程中有重复的点就输出 True，如果没有重复的点就输出 False

数据范围：10^4，时间复杂度要控制在 O( n√ n ) 或者 O(nlogn)

每次只走一单位的距离，而且是横平竖直的方式走，每次走完之后走过的所有点都一定是整数点（横纵坐标都一定是整数），如果走过重复的点一定是某一个线段的两端，不可能走到两条线之间中点的位置，只需要考虑它所有走过的端点有没有重复的点即可（可以用哈希表判断一堆点里面有没有重复的点）

用哈希表把所有走过的点都存储下来，每次走到一个新的点之后，如果我们发现这个新的点之前走过，就返回 True，否则返回 False

注意哈希表只能哈希一部分的变量类型，例如：哈希表可以哈希 string，但是不能哈希 pair，给我们一个坐标（x，y），需要把它变成哈希表能够哈希的类型（一种比较简单的方式是把 x、y 拼接成一个字符串）

时间复杂度与走过的点数成正比，时间复杂度为 O( n )

class Solution {
public:
    bool isPathCrossing(string path) {
        //定义一个哈希表
        unordered_set<string> hash;
        //先把起点(0,0)加到哈希表中
        hash.insert("0 0");
        //起点(0,0)
        int x = 0, y = 0;
        //枚举每一个指令
        for(auto c: path) {
            //如果指令为'N' 表示我们应该向上走
            if(c == 'N') x --;
            else if(c == 'S') x ++;
            //向左走
            else if(c == 'W') y --;
            else y++;
        //把当前坐标变成一个字符串
        string s = to_string(x) + ' ' + to_string(y);
        //如果s在之前出现过-> 说明有重复的点
        if(hash.count(s)) return true;
        //否则把当前坐标加到哈希表中
        hash.insert(s);
        }
        //如果整个过程没有发现重复的点 返回false
        return false;
    }
};

检查数组对是否可以被 k 整除

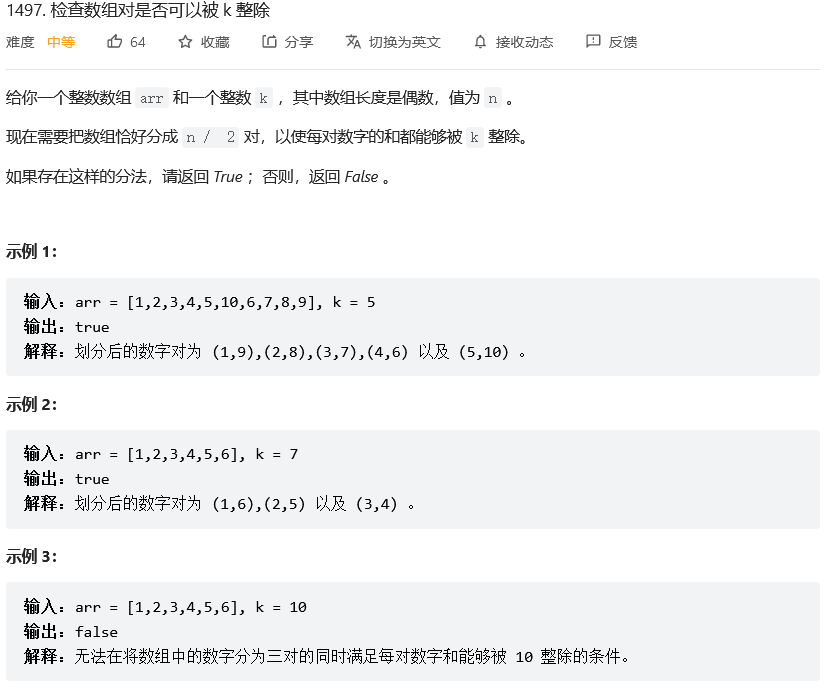
给出一个数组，再给一个 k，数组长度是偶数，希望把数组中的所有数分成两两一组配对，使得每一对的数字之和都恰好能够被 k 整除，如果可以满足返回 True，否则，返回 False

数据范围：10^5，时间复杂度要控制在 O(nlogn)

配对的方式有很多种，方案数可能有指数级别。要让每一对的数的和能够被 k 整除，我们关心应该不是 a、b 的绝对值，应该是 a 和 b 除以 k 的余数：如果 a  + b 能够被 k 整除，意味着 k / (a + b) 的余数是 0，应该关心每一个数对里面每一个数的余数是多少

先将数组里面的所有数分成 k 类（根据它对于 k 的余数分成 k 类）

余数从 0 ~ k - 1，一共有 k 种

在配对的过程中：

如果当前这个数除以 k 的余数是 0，如果想让这一对数的和除以 k 的余数也是 0，必须要求与它配对的这个数除以 k 的余数也是 0，余数是 0 的数只能和 0 配对，余数是 1 的数只能和余数是 k - 1 的数配对，余数是 2 的数只能和余数是 k - 2 的数配对. . .以此类推，可以发现虽然方案很多，但是是确定性的配对，我们只需要检查一下：按照这种配对方式，能不能恰好分成 k 组即可（每一个数都找到它配对的数）

先统计一下每一类的数的个数，先判断余数是 0 这一类的个数是不是偶数（ 0 只能和 0 配对），再判断余数是 1 这一类的个数和余数是 k - 1 这一类的个数是不是一样的. . .以此类推

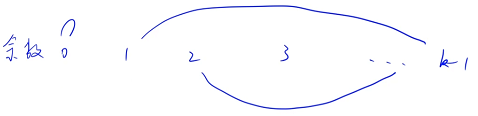
直接模拟，一个个数配对：对于 0 要与 0 配对，对于 1 要与 k - 1 配对，每有一个 1 就要有一个 k - 1 和它配对，当有一个 1 但是没有 k - 1 就矛盾了，把 1 配对完后再看 2，以此类推. . .如果每一个数都可以配对，返回 True；如果不可以配对，返回 False

对于负数情况的判断参考题解： leetcode1497_Jackybored的博客-CSDN博客_力扣1497

仔细读题可发现突破点，首先每对数字，是否存在说明我们需要遍历数组并且记录下数字的某些信息，这样才能用于之后的存在查找操作。匹配条件是被k整除就该想到使用取模操作。这时将匹配条件转换成取模操作就可解决。如果两个整数相加是k的倍数，那么两个数均取模再相加和必为k。这里分三种情况讨论：

1.一个数是正的，一个数是负的，这样两数和为 0，可以被 k 整除，那么我们该如何匹配这两个数呢，应该如下操作，对于负数 num，进行 (num%k) + k 操作,如 num = -1，k = 3，那么 (-1%3) + 3 = 2，和 -1 匹配的数是 1，对正数进行 num%k 操作，1%3 = 1。可以发现这两个操作之后的数相加为 3，即2 +1 = 3，因此可转化为进行上述操作后结果相加为 k，类似于两数之和的匹配问题。
2.两个数都是正的，和为k的倍数，如 num1 = 4，num2 = 5，k = 3，那么进行 num%k 操作可得到 4%3 = 1，5%3 = 2，1+2=3，匹配条件和上述相同。
3.如果两个数本身就是k的倍数，如num1 = 3，num2 = 3，k = 3，那么 3%3 = 0，这时我们需要记录取余操作为 0 的个数，如果个数是奇数个，必定有一个数无法匹配。

其实对于取余操作来说，进行多次取余操作对结果是没有影响的，如 5%3 = 2，5%3%3 = 2，因此正数情况和负数情况可以合并到一起，即((num%k)+k)%k，这样我们就可以写出代码，不一定需要使用hash_map记录，其它的数据结构 vector 等均可记录

class Solution {
public:
    bool canArrange(vector<int>& arr, int k) {
        //开一个哈希表记录每一类数的个数
        unordered_map<int,int> cnt;
        //统计每一类数
        //取模负数余数为负数需要做考虑-> 需要把所有的余数变成非负数
        for(auto x : arr) cnt[(x % k + k) % k] ++;

        //先判断第 0 类是不是满足要求-> cnt[0] %2 ?= 1 偶数个成立、奇数个不成立
        if(cnt[0] % 2) return false;
        //从第 1 类开始一直到第 k - 1 类
        for(int i = 1;i < k;i++) {
            //如果当前类有数
            while(cnt[i]) {
                //当前类--
                cnt[i] --;
                //看第 k - i 类有没有对应的一个数 如果第 k - i 类已经小于等于 0,说明当前第 i 类这个数无法配对
                if(cnt[k - i] <= 0) return false;
                //减去与当前数配对的数
                cnt[k - i] --;
            }
        }
        //每一个数都可以配对
        return true;
    }
};

满足条件的子序列数目

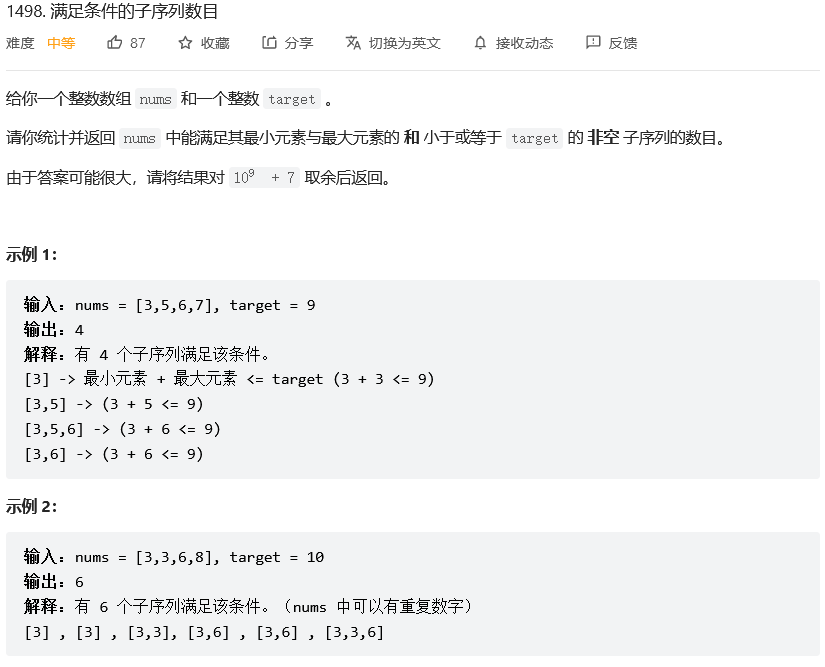
给出一个数组 nums 和一个目标值 target，统计数组中有多少个非空子序列，使得子序列中的最小元素与最大元素的和小于等于 target，返回其数目

数据范围：10^5，时间复杂度要控制在 O(nlogn)

找一个序列的子序列等价于找它的子集：任何一个子序列都是一个集合，任何一个集合按照下标排序都是一个子序列

给出我们一堆数，要看一下这堆数里面，有多少个非空子集，使得非空子集的最大数加最小数小于等于目标值 target，要考虑一个集合的最大元素和最小元素，为了方便找到集合的最大元素和最小元素，可以先将整个数组从小到大排序，最靠前的就是最小值，最靠后的就是最大值

统计有多少个子集，使得最小数和最大数的和是小于等于目标值 target

带有所有子集的集合如下所示：

为了方便统计子集的数量，可以把所有子集分类，按最大元素分类（或者按照最小元素分类），所有最小元素是第 0 个数的子集是第 1 类，所有最小元素是第 1 个数的子集是第 2 类，以此类推一直到第 n - 1 类，只需分别求出每一类的子集数量，加在一起，就是所有满足要求的非空子集的数量

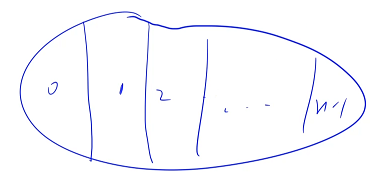
考虑当前第 i 类，假设最小元素是 ai（由于 ai 是最小值，所以 ai 左边的数都不能选或者没有左边的数），由于 ai 是最小元素，所以在选择元素的时候，只能在 ai 的右边选，要求最大元素加最小元素要小于目标值：从 i 开始，在右边找最大元素最大是多少的时候可以满足要求

假设对于 ai 来说，可以找到一个最大的 aj，ai + aj 是小于等于目标值 target，并且 aj 是临界点（aj 是最大的所有满足要求的数，aj 右边所有的数都不能选）

最小元素是 ai 的，所有满足要求的非空子集有多少个？怎么计数？

只能从 ai 到 aj 之间的这些数中做选择，由于是第 i 类，首先必须包含 ai

剩下的 ai-1 ~ aj-i 之间的 j - i 个数选或者不选都是满足要求的，每个数都有两种选法

第 i 类总共的方案数是 2^j-i 个

 

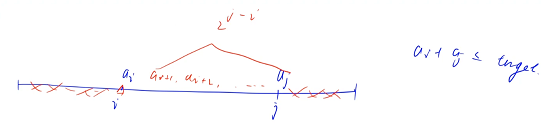
只要对于每一个 ai ，找到一个最大的 aj，就可以统计出第 i 类满足要求的子集数量

怎么对于每一个 ai 找 aj？由于整个序列递增，可以用双指针

如果从前往后枚举 ai 的值，ai 是不断变大的，与之对应的 aj 是不断变小的

一开始 i 在第 0 个位置，i 从左往右走，j 在最后一个位置，从右往左走，i 越大，j 越小

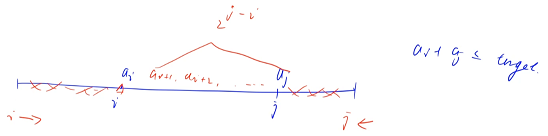
双指针能够使用的前提：有单调性，当 i 从前往后走的时候，j 一定会从后往前走，j 不可能往后走，j 的走法是单调的

当 i 从 i 走到 i ' 的时候，与 i ' 相对应的 j ' 不可能在 j 的后面，如果 i ' + j ' 这两个数小于等于目标值，那么 i  + j ' 这两个数也一定小于等于目标值，（因为 i 变小了），意味着第 i 个数对应的 j 就不是最大的 j，就会出现矛盾，所以 j 的走法具有单调性，可以用双指针

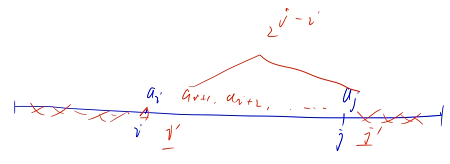
要考虑重复计数的问题，题目并没有告诉我们所有的数是不重复的，当我们有相同的数据的时候怎么处理？

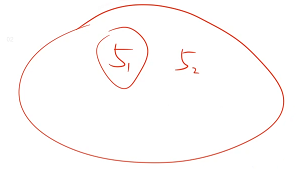
当某一个集合中包含两个 5 的时候，最小值应该取哪个 5？（取第 1 个 5、取第 2 个 5、都可以取）会不会出现重复计数？会不会导致这个子集在枚举一个 5 的时候被记录一次，在枚举第 2 个 5 的时候，又被记录一次从而导致重复计数？

答案是肯定的，但是我们可以把它规避：虽然这两个 5 的数值是一样的，但是，可以人为规定它们的先后顺序：规定排序后靠前的 5 比靠后的 5 要小，这样就不会出现重复计数的问题

从而保证每一个集合的最小值和最大值都是唯一的，每个集合在计数的时候，只会被它的唯一最小值记录一次，从而不会出现重复计数

整个算法的时间复杂度为 O(nlogn) （排序）

双指针时间复杂度：O(n)

需要计算 2^j-i，2^j-i 可能很大，需要先预处理

leetcode1498. 满足条件的子序列数目（Python3）_AndyLiu1997的博客-CSDN博客

首先我们发现，非空子序列不需要是子数组，也就是说，与数组原有顺序无关。且满足条件的序列满足最大值和最小值的和小于等于target。因此我们可以直接对数组进行排序，这样我们就可以划定范围，对某一个子数组，最左边的值一定是子数组的最小值，最右边的值一定是最大值。

下面我们考虑上面的子数组，如果对于一个子数组，使用双指针，left表示子数组的左边界，right表示数组右边界，那如果

left+right <= target，那么这个子数组中有多少序列满足条件呢？答案是2 ^ (right-left)。

这里面我们的序列必须包含nums[left]，以子数组[2,3,4,6]，target=9为例：

我们必须含有2，那么所有符合条件的序列为[2]、[2,3]、[2,4]、[2,6]、[2,3,4]、[2,3,6]、[2,4,6]、[2,3,4,6]。一共2 ^ 3=8个。

解释起来就是，在必须包含2的基础上，后面的3个数可以选0个、选1个、选2个、选3个。即Cn0 + Cn1 + … + Cnn = 2 ^ n。

那么我们为什么必须包含2呢，为什么不考虑[3]、[4]等等呢？

原因是这些答案在之后的循环中会被找到。

所以我们每次计算的是以left位置为起止的，所有满足条件的序列。

我们首先将左右指针设为整个数组的左右两端；如果此时不满足条件，则右指针right–，直到找到与此时的left满足条件的right。当左右指针的和满足条件（小于等于target），那么计算此时以left为起始的所有子序列；然后left++，继续计算。

【C++ 取模mod易错点】由于答案可能会很大，请你将结果对1e9+7取模后再返回_白马金羁侠少年的博客-CSDN博客_c++ mod

取模运算（C++）_还没想好~的博客-CSDN博客_c++整除符号

class Solution {
public:
    int numSubseq(vector<int>& nums, int target) {
        int n = nums.size(),mod = 1e9 + 7;
        vector<int> p(n);
        //预处理 2 的所有次幂
        //p[0]为2^0
        p[0] = 1;
        for(int i = 1;i < n; i++ ) p[i] = p[i - 1] * 2 % mod;
        //给数组排序
        sort(nums.begin(),nums.end());
        int res = 0;
        //从前往后用双指针算法枚举
        for(int i = 0,j = n - 1;i < n;i++ ) {
            //j不能在i的前面-> i是最小值 不能选i前面的数
            while(j >= i && nums[i] + nums[j] > target) j--;
            if(j >= i && nums[i] + nums[j] <= target) {
                //满足要求记录答案 res加上2^j-i
                res = (res + p[j - i]) % mod; 
            }
        }
        return res;
    }
};

满足不等式的最大值