试除法求约数
和<试除法判断一个数是不是质数>是一个道理
从小到大枚举所有的约数,如果当前数能整除这个数的话,说明这个数就是当前数的约数
优化,与<试除法判断质数>是一样的
如果 d 是 n 的约数,n / d 也一定能整除 n,一个数的约数也一定是成对出现的,在枚举的时候也可以只枚举较小的那个约数,较大的那个约数可以直接计算,只需要枚举到 d ≤ n / d,d ≤ √ n 就可以了
时间复杂度为 O( n × √ a ),100 × ( √ 2 × 10^9 )
4 w^2 = 1.6 × 10^9 < 2 × 10^9 < 5w^2 = 2.5 × 10^9
4 w < √ 2 × 10^9 < 5w
√ 2 × 10^9 介于 4w 到 5w 之间,整个算法的时间复杂度在 400w 到 500w 之间
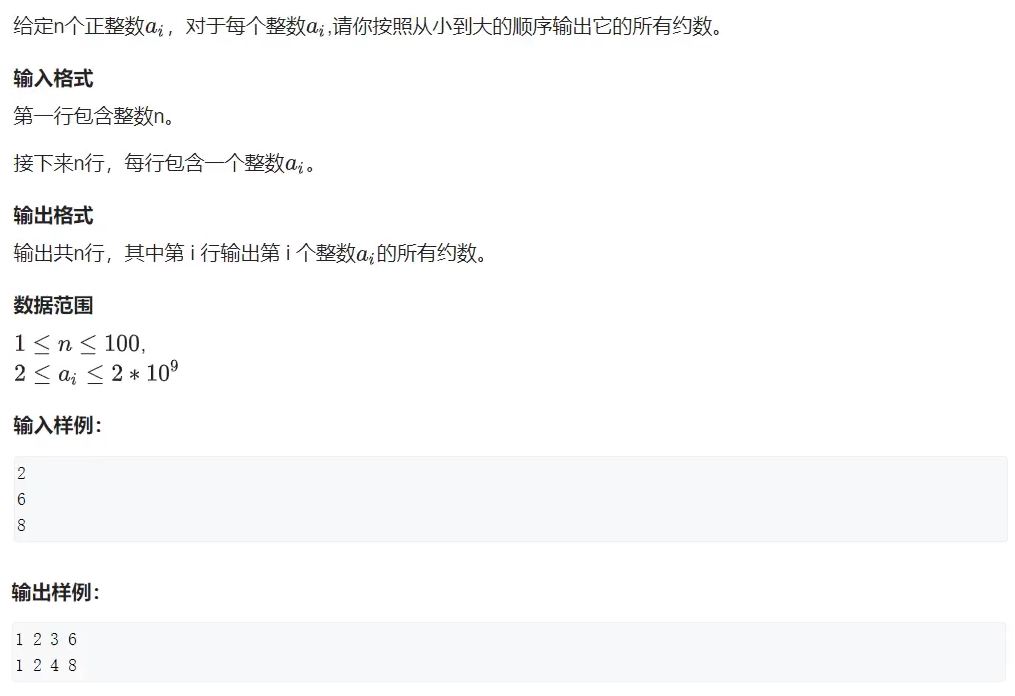
#include <iostream>
#include <algorithm>
//用 vector 存储一个数的所有约数
#include <vector>
using namesapce std;
//试除法求 n 的所有约数
vector<int> get_divisors(int n)
{
//答案数组
vector<int> res;
//从小到大枚举 n 的所有约数 但是只枚举每一对约数里面较小的那个
for(int i = 1;i <= n / i;i++ )
//如果 n % i == 0,i 一定是 n 的约数
if(n % i == 0)
{
res.push_back(i);
//n / i 也是约数,但是需要判断边界情况:有可能 n 是 i 的平方,两个约数一样,但是输出的时候不能重复
if(i != n / i) res.push_back(n / i);
}
//给约数排序
sort(res.begin(),res.end());
return res;
}
int main()
{
int n;
cin >> n;
while(n-- )
{
int x;
cin >> x;
//求所有的约数
auto res = get_divisors(x);
//遍历然后输出
for(auto t : res) cout << t << ' ';
cout << endl;
}
return 0;
}求一个数的所有约数个数、所有约数之和
基于算术基本定理,对于一个整数 N 分解质因数的结果为 p1^α1 * p2^α2 * . . . * pk^αk
约数个数:(α1 + 1) * (α2 + 1) * . . . * (αk + 1),N 的约数个数和选法个数是一样的,乘法原理
约数之和:(p1^0 + p1^1 + . . . + p1^α1) * . . . * (pk^0 + pk^1 + . . . + pk^αk)
int 范围内约数个数最多的一个数最多有 1500 个约数
时间复杂度为 O( n )

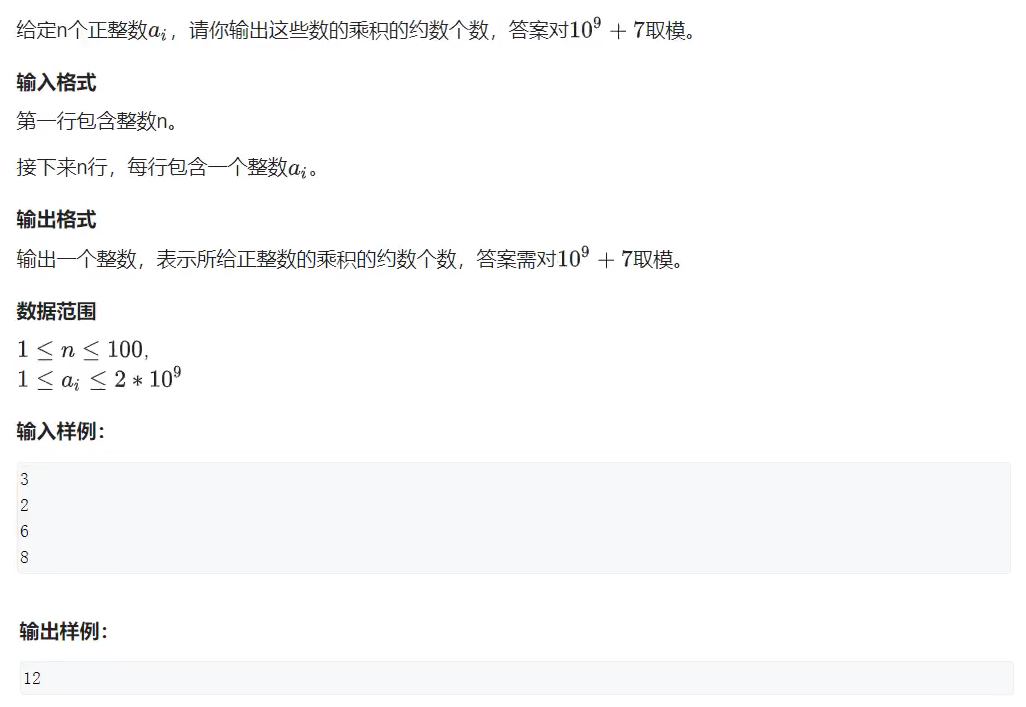
给定 n 个整数 a1 ~ an,要求统计所有数乘积 a1 × a2 × . . . × an 的约数个数,先求 a1 ~ an 每一个数分解质因数的结果,然后把每一个数的指数累加在一起就可以了,从 a1 开始分解,一直分解到 an,假设求出来 a1 的某一个质因子 pi 的指数是 αi,可以用一个哈希表或者 map 把它存储下来,把每一项都分解完之后,map 中存储了整个乘积的因式分解的底数和指数,最终约数个数就是所有指数加 1 再相乘
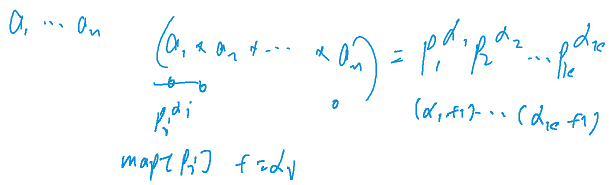
#include <iostream>
#include <algorithm>
// 这里选择使用哈希表
#include <unordered_map>
using namesapce std;
typedef long long LL;
const int mod = 1e9 + 7;
int main()
{
int n;
cin >> n;
// 定义哈希表存储所有底数和指数
unordered_map<int,int> primes;
while(n --)
{
int x;
// 读入 x 然后把 x 分解
cin >> x;
// 从 2 开始枚举 分别分解每一个数,首先对于 a1 来说,把 a1 的所有质因子的次数找出来然后累加就可以了
for(int i = 2;i <= x / i;i++ )
while(x % i == 0)
{
x /= i;
// i 的质因数的指数 + 1 最终 primes 里面存储了所有质因数的指数
primes[i] ++;
}
//特判 x > 1 说明 x 是一个比较大的质因数 把剩下这个质因数加上就可以了
if(x > 1) primes[x] ++;
}
LL res = 1;
// 枚举所有质因数 答案就是所有的指数 + 1 再相乘
for(auto prime : primes) res = res * (prime.second + 1) % mod;
cout << res << endl;
return 0;
}只要能求出一个数质因数分解的结果,就可以分别求出约数个数和约数之和
求约数之和:也需要先分解质因数,然后直接带入求和公式就可以了
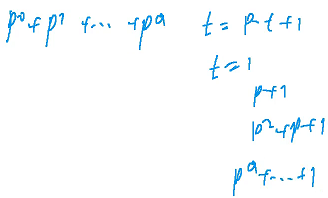
#include <iostream>
#include <algorithm>
// 这里选择使用哈希表
#include <unordered_map>
using namesapce std;
typedef long long LL;
const int mod = 1e9 + 7;
int main()
{
int n;
cin >> n;
// 定义哈希表存储所有底数和指数
unordered_map<int,int> primes;
while(n --)
{
int x;
// 读入 x 然后把 x 分解
cin >> x;
// 从 2 开始枚举 分别分解每一个数,首先对于 a1 来说,把 a1 的所有质因子的次数找出来然后累加就可以了
for(int i = 2;i <= x / i;i++ )
while(x % i == 0)
{
x /= i;
// i 的质因数的指数 + 1 最终 primes 里面存储了所有质因数的指数
primes[i] ++;
}
//特判 x > 1 说明 x 是一个比较大的质因数 把剩下这个质因数加上就可以了
if(x > 1) primes[x] ++;
}
LL res = 1;
// 枚举所有质因数 答案就是所有的指数 + 1 再相乘
for(auto prime : primes)
{
//先枚举每一个质数 p表示这个质数的底数 a表示这个质数的指数
int p = prime.first,a = prime.second;
//需要求出来 p^0 + p^1 + ... + p^a
//用 t 来表示总和,t 从 1 开始
LL t = 1;
//执行 a 次 t * p + 1 就可以得到 p^0 + p^1 + ... + p^a
while(a -- ) t = (t * p + 1) % mod;
res = res * t % mod;
}
cout << res << endl;
return 0;
}公式推导:约数和定理,约数个数定理

怎么求一个数的约数呢?
利用短除法对 72 进行分解质因数得到 72 = 2^3 × 3^2,2 是质数,3 是质数,2 与 3 都是 72 的质因数
为什么要对 72 进行分解质因数呢?
因为 72 这个合数的任意一个约数,都可以表示成 2^x 3^y
无论多大的数只要能够分解质因数,都能够把它的约数造出来

接下来求 360 的正约数,我们通过短除法把它的正约数造出来,有多少种造法就有多少个正约数

利用原材料 2,可以取零个 2、一个 2、两个 2、三个 2,一共有 4 种方法
利用原材料 3,一共有 3 种方法
利用原材料 5,一共有 2 种方法
把每个质因数上的指数 + 1 再相乘,就得到某一个数的正约数的个数
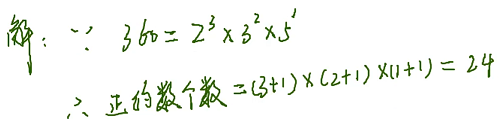
接下来求所有正约数之和,首先如果要把 360 的正约数全部穷举出来就是一个不小的工程,还需要求和,工程较大,容易出错,因此我们还是用造的思想把约数给造出来
我们可以利用分类讨论的思想,以 2 为原材料可以造出 2^0、2^1、2^2、2^3,以 2 和 3 为原材料,以此类推
第一类方案与第二类方案的总数之和如下
利用 2、3、5 与 利用 2、5 来造 360 的约数,可以发现 2、3 已经造好了,只需要乘上一个 5 就可以了
在利用 2、3、5 造约数的过程中,已经把 3、5 的情况包括在内: 2^0 × 3^1、2^0 × 3^2
得到最终所有正约数的总和就是 ( 2^0 + 2^1 + 2^2 + 2^3) × (3^0 + 3^1 + 3^2) × (1 + 5^1)
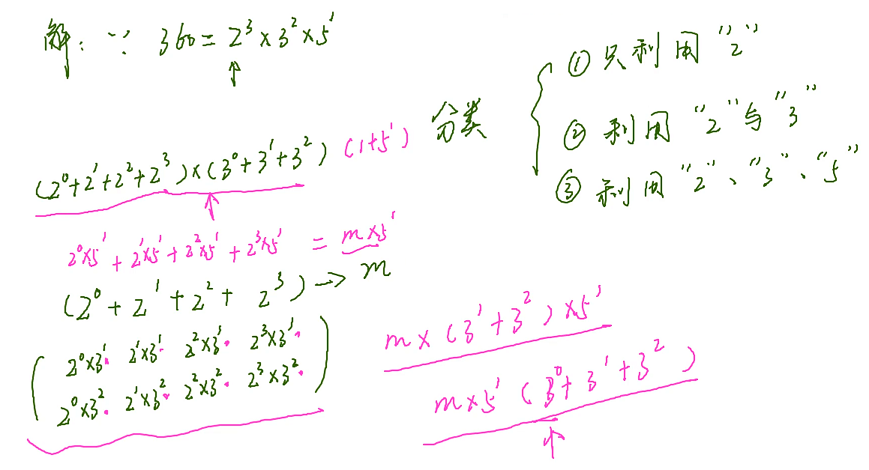
不穷举,采用提取公因式的方式,先得到 2 和 3 参与的,后得到 2、3、5 参与的


欧几里得算法 / 辗转相除法
数论中的基本性质:
如果 d 能整除 a,并且 d 能整除 b,d 就能整除 a + b,也能整除 a 的若干倍 + b 的若干倍
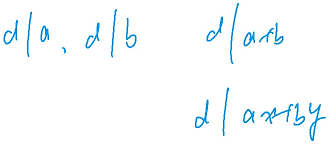
辗转相除法的核心原理:
利用这个性质,a 和 b 的最大公约数等于 b 和 a mod b 的最大公约数
![]()
怎么证明左右两边的最大公约数是相同的呢?
a 和 b 的最大公约数等于 b 和 a - c × b 的最大公约数
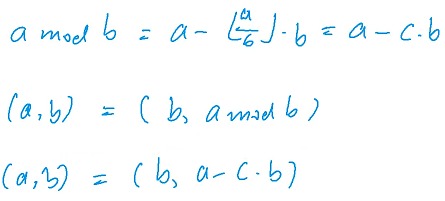
证明可以利用如下性质
对于左边的任何一个公约数 d 能整除 a,d 能整除 b,所以 d 能整除 b,所以 d 能整除 a - c × b,所以左边的任何一个公约数都是右边的一个公约数
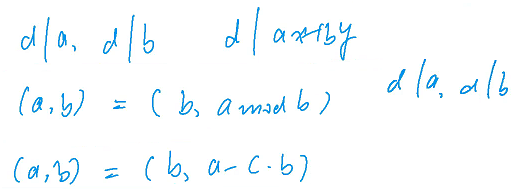
证明右边的任何一个公约数也是左边的一个公约数
d 能整除 b,d 能整除 a - c × b,所以 d 能整除 b,只需要证明 d 能整除 a 就可以了
d 能整除 a - c × b,所以 d 能整除 a - c × b × 1 + b × c,抵消后 d 能整除 a,所以右边任何一个公约数都是左边的一个公约数
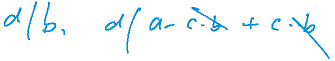
同样左边任何一个公约数都是右边的一个公约数,所以这两个公约数的集合相同的,最终得证左边的最大公约数等于右边的最大公约数,所以可以直接用性质来计算最大公约数
最大公约数
给出 n 组 a、b,求每一组的最大公约数,时间复杂度 O( logn )
#include <iostream>
using namespace std;
// 返回 a 和 b 的最大公约数
int gcd(int a,int b)
{
// 如果 b 不是 0,返回 gcd(b,a % b),当 b 等于 0 的时候,a 和 0 的最大公约数一定是 a,因为 0 可以整除任何数
return b ? gcd(b,a % b) : a;
}
int main()
{
int n;
scanf("%d",&n);
while(n-- )
{
int a,b;
//每次读入两个数
scanf("%d%d",&a,&b);
//返回 a 和 b 的最大公约数
printf("%d\n",gcd(a,b));
}
return 0;
}



 本文介绍了利用试除法求解整数的约数及其优化,以及如何根据质因数分解计算约数个数和约数之和。通过举例和代码实现,详细阐述了数论中的基本算法,如试除法、欧几里得算法,并展示了在C++中的应用。
本文介绍了利用试除法求解整数的约数及其优化,以及如何根据质因数分解计算约数个数和约数之和。通过举例和代码实现,详细阐述了数论中的基本算法,如试除法、欧几里得算法,并展示了在C++中的应用。
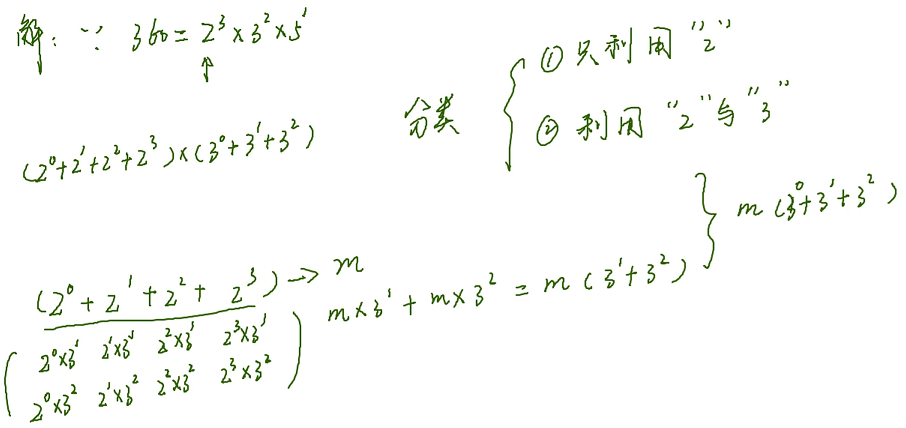


















 3826
3826

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










