什么是跳表
跳表(Skip List)是一种随机化的数据结构,基于并联的有序链表,其效率可比拟于二叉搜索树(如红黑树、AVL树等)。跳表的平均查找和插入时间复杂度都是O(log n),但与平衡树相比,跳表的实现更为简单,且常数因子更小。
跳表是对有序链表的一种扩展,通过维护一系列分层的链表,并在每一层中跳过部分元素,从而加快查找速度。跳表上层的链表作为下层链表的"快速通道",使得在查找时可以先在高层链表中进行大步跳跃,再在底层链表中进行精确定位。
为什么需要跳表?
传统的有序链表虽然插入和删除操作比较方便(只需要修改指针),但查找操作需要从头开始遍历,时间复杂度为 O(n)。如果链表很长,查找效率会非常低。
平衡树(如 AVL 树、红黑树)可以实现 O(logn) 的查找、插入和删除,但它们的实现比较复杂,需要进行旋转等操作来维护树的平衡。
跳表提供了一种折衷方案:它在实现复杂度上接近链表,但在性能上接近平衡树。
基本原理
基本结构
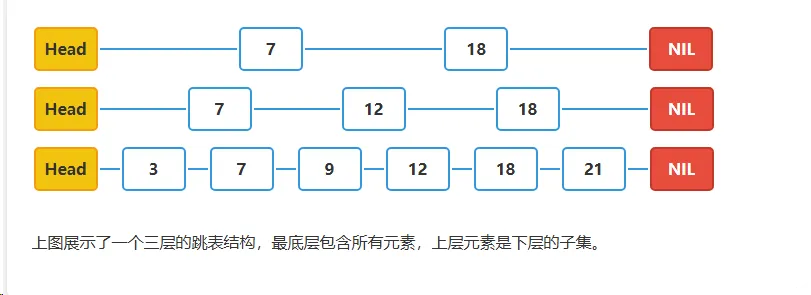
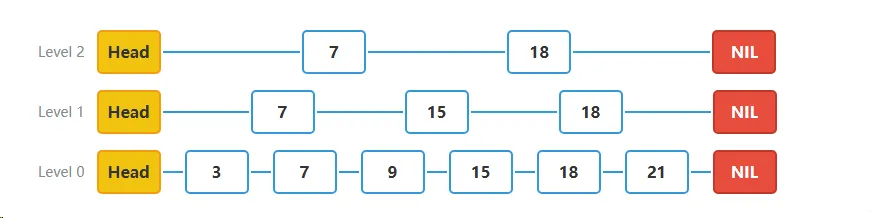
跳表由多层链表组成,每一层都是一个有序链表,底层包含所有元素,而上层则是下层的子集。具体来说:
- 最底层(Level 0)是一个普通的有序链表,包含所有元素
- 第一层(Level 1)大约包含每两个元素中的一个
- 第二层(Level 2)大约包含每四个元素中的一个
- 依此类推,第i层大约包含每2^i个元素中的一个
节点结构
每个跳表节点包含:
- 值(key):节点存储的实际数据
- 多个前向指针:指向同层的下一个节点
- 层数(level):决定节点在哪些层出现
/**
* 跳表节点类
*/
class SkipListNode {
Integer key;
SkipListNode[] forward;
public SkipListNode(Integer key, int level) {
this.key = key;
this.forward = new SkipListNode[level + 1];
}
@Override
public String toString() {
return "SkipListNode(key=" + key + ")";
}
}
跳表核心操作
随机层数的生成
跳跳表使用类似于抛硬币的方式来决定一个新节点的层数:
- 新节点默认在最底层(Level 0)出现
- 使用概率参数p(通常为0.5或0.25)决定是否上升到更高层
- 生成一个随机数r在[0,1]范围内
- 如果r < p,则层数加1,节点会出现在Level 1
- 继续生成随机数和比较,直到某次r >= p或达到最大层数
这种随机层数生成机制的特点是:
- 每个节点至少在Level 0层出现
- 每一层上的节点数量大约是下一层的一半(当p=0.5时)
- 最底层包含所有节点,向上每层节点数量递减
- 平均来说,大约有1/2的节点会出现在Level 1
- 大约有1/4的节点会出现在Level 2
- 大约有1/8的节点会出现在Level 3
- 以此类推…
private int randomLevel() {
int level = 0;
while (random.nextDouble() < P && level < MAX_LEVEL) {
level++;
}
return level;
}
搜索操作
示例代码
跳表的搜索从最高层开始,然后逐层向下:
- 从头节点的最高层开始
- 如果当前节点的前向指针指向的节点值小于目标值,则向前移动
- 否则,降低一层继续搜索
- 重复上述过程,直到达到最底层并找到目标值或确定其不存在
public SkipListNode search(int key) {
SkipListNode current = this.header;
//从最高层开始,逐层向下查找
for (int i = this.level; i >= 0; i--) {
//在当前层水平移动,知道找到小于或等于目标值的最大节点
while (current.forward[i] != null && current.forward[i].key < key) {
current = current.forward[i];
}
}
//现在在底层,检查下一个节点是否是目标值
current = current.forward[0];
//如果下个节点存在并且key相等,则找到目标
if (current != null && current.key == key) {
return current;
}
return null;//未找到目标
}
查找步骤

查找值为12的节点的过程。搜索从头节点的最高层开始,逐层向下进行。
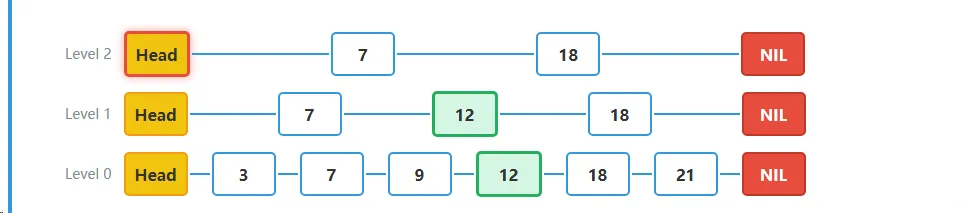
步骤一从最高层开始搜索:
- 搜索从跳表的最高层(Level 2)的头节点开始。我们要查找值为12的节点。
- 当前位置:Level 2的Head节点
- 目标:找到值为12的节点
步骤二在最高层水平移动到合适位置:
- 在Level 2层,Head的next指向值为7的节点。因为7 < 12,所以我们移动到值为7的节点。
- 当前位置:Level 2的节点7
- 判断:7 < 12,可以继续向右移动
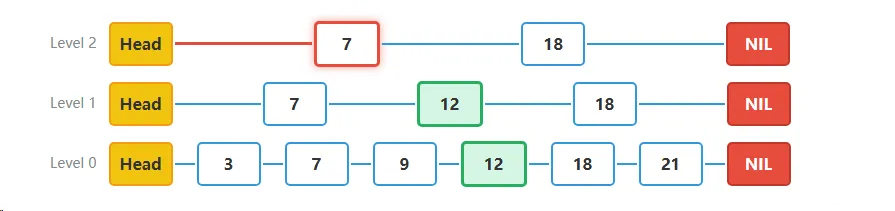
步骤三当前层无法继续前进,降低层级:
- 在Level 2层,节点7的next指向值为18的节点。因为18 > 12,所以我们无法继续向右移动。此时需要降到Level 1层继续搜索。
- 当前位置:Level 1的节点7
- 判断:在Level 2中,下一个节点值18 > 12,无法继续水平移动,需要降级
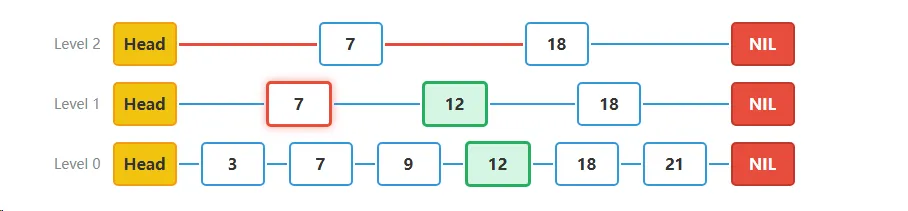
步骤四在中间层继续搜索:
- 在Level 1层,节点7的next指向值为12的节点。因为12 = 12,我们找到了目标值,但仍然需要降到最底层以确认节点是否存在于最底层。
- 当前位置:Level 1的节点12
- 判断:12 = 12,找到目标值,继续降级到最底层确认
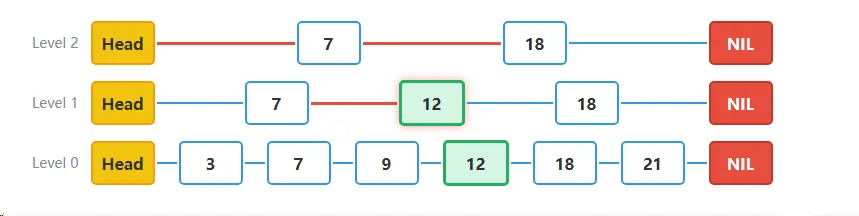
步骤五在最底层确认结果:
- 在Level 0(最底层),我们确认值为12的节点确实存在。搜索成功完成。
- 当前位置:Level 0的节点12
- 结果:成功找到目标节点12
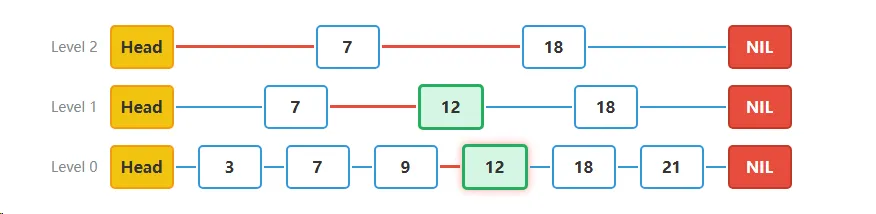
搜索路径总结:
- 从Level 2的Head节点开始
- 移动到Level 2的节点7
- 发现下一个节点18 > 12,降到Level 1
- 在Level 1找到节点12,等于目标值
- 降到Level 0确认节点12存在
- 搜索成功完成
搜索操作的时间复杂度为O(log n),因为我们利用了跳表的分层结构,每一层大约跳过了一半的节点。
插入操作
示例代码
跳表的插入过程包括:
- 搜索合适的插入位置,同时记录每一层需要更新的节点
- 为新节点随机生成一个层数
- 如果新节点的层数高于当前跳表的层数,更新跳表层数
- 更新所有受影响层的前向指针
public boolean insert(int key) {
// 创建更新数组,用于存储需要更新前向指针的节点
SkipListNode[] update = new SkipListNode[MAX_LEVEL + 1];
SkipListNode current = this.header;
// 从最高层开始,查找适合的插入位置
for (int i = this.level; i >= 0; i--) {
while (current.forward[i] != null && current.forward[i].key < key) {
current = current.forward[i];
}
// 记录每一层需要更新的节点
update[i] = current;
}
// 移动到下一个节点
current = current.forward[0];
// 检查key是否已经存在
if (current != null && current.key == key) {
return false;// key已存在,则插入失败
}
// 为新节点生成随机层数
int randomLevel = randomLevel();
if (randomLevel > this.level) {
// 更新跳表当前最大层数
for (int i = this.level + 1; i <= randomLevel; i++) {
update[i] = this.header;
}
this.level = randomLevel;
}
// 创建新的节点
SkipListNode newNode = new SkipListNode(key, randomLevel);
// 更新所有受影响的前向指针
for (int i = 0; i <= randomLevel; i++) {
newNode.forward[i] = update[i].forward[i];
update[i].forward[i] = newNode;
}
return true;
}
插入步骤
如下在跳表中插入值为15的新节点的过程。插入操作包括查找位置、记录更新路径、生成随机层数和更新指针。
步骤一查找插入位置并记录更新路径:
- 我们要插入值为15的新节点。首先需要从最高层开始,找到合适的插入位置,并记录每层需要更新的节点。
- 当前位置:Level 2的Head节点
- 目标:找到值为15应该插入的位置
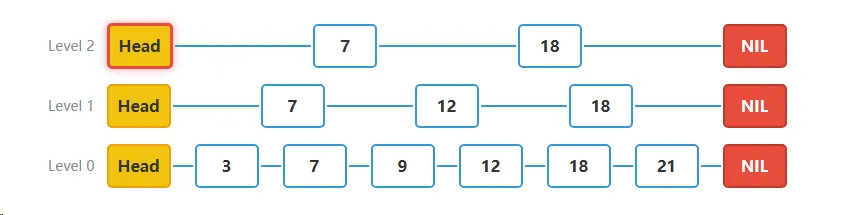
步骤二**Level 2层搜索**:
- 在Level 2层,当前位置是节点7。其下一个节点是18,因为18 > 15,所以我们不能继续向右移动。记录节点7为Level 2层需要更新的节点。
- 当前位置:Level 2的节点7
- 判断:下一个节点18 > 15,无法继续右移,记录update[2] = 7
- 降级到Level 1继续搜索
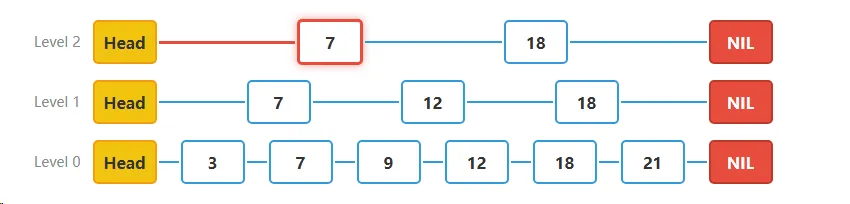
步骤三**Level 1层搜索**:
- 在Level 1层,我们移动到值为12的节点。下一个节点是18,因为18 > 15,所以记录节点12为Level 1层需要更新的节点。
- 当前位置:Level 1的节点12
- 判断:下一个节点18 > 15,无法继续右移,记录update[1] = 12
- 降级到Level 0继续搜索
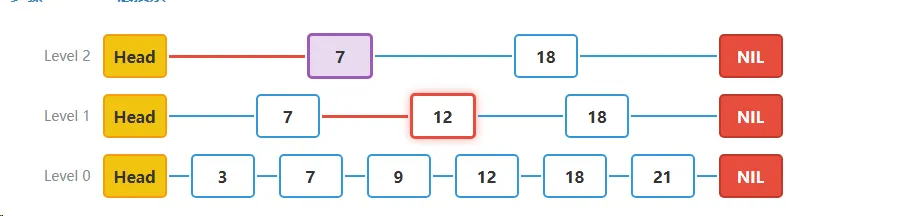
步骤四**Level 0层搜索**:
- 在Level 0层,我们当前在节点12。下一个节点是18,因为18 > 15,所以记录节点12为Level 0层需要更新的节点。
- 当前位置:Level 0的节点12
- 判断:下一个节点18 > 15,无法继续右移,记录update[0] = 12
- 此时我们已经找到了每一层需要更新的节点:
- Level 2: 节点7
- Level 1: 节点12
- Level 0: 节点12
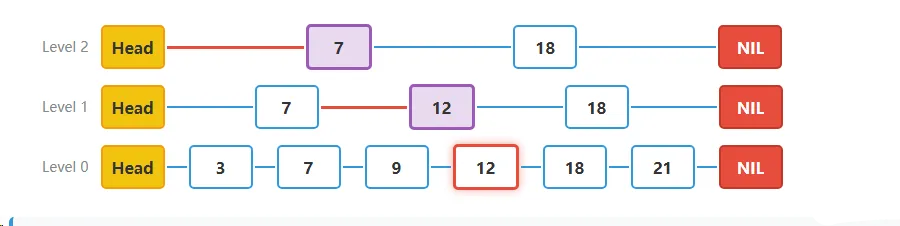
步骤五**为新节点生成随机层数**:
- 接下来,我们需要随机生成新节点的层数。假设随机生成的层数为1,那么新节点将出现在Level 0和Level 1层中。
- 随机生成层数:1
- 这意味着新节点15将出现在Level 0和Level 1层中
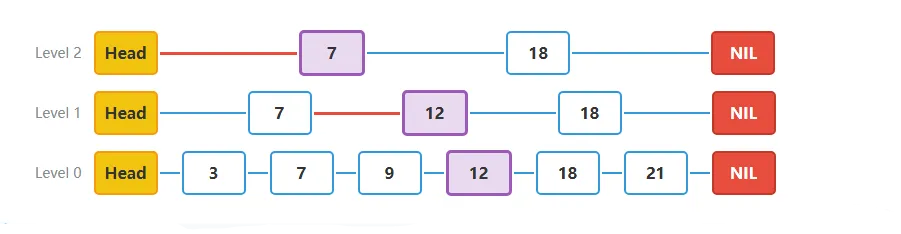
步骤六**创建新节点并在Level 0层插入**:
- 我们创建一个值为15的新节点,并在Level 0层插入。
- 更新Level 0层的指针:
- 新节点15的next指向原来12节点指向的18节点
- 12节点的next指向新的15节点

步骤七**在Level 1层插入**:
- 接下来,我们在Level 1层插入新节点。
- 更新Level 1层的指针:
- 新节点15的next指向原来12节点指向的18节点
- 12节点的next指向新的15节点

步骤八**插入完成**:
- 插入操作完成,新节点15已成功插入到跳表中的Level 0和Level 1层。
- 结果:
- 新节点15出现在Level 0和Level 1层
- 所有相关的指针都已更新
- 跳表的结构保持有序
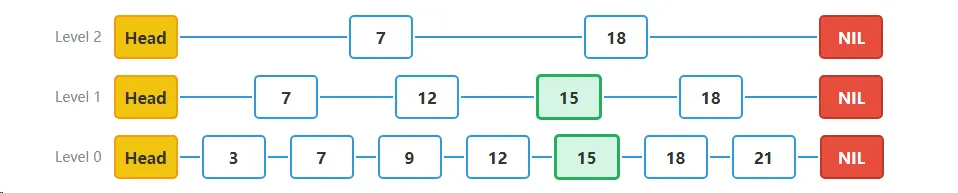
插入操作总结:
- 首先从最高层开始,查找合适的插入位置,并记录每一层需要更新的节点
- 检查目标值是否已存在于跳表中,如果存在则插入失败
- 为新节点随机生成一个层数
- 创建新节点,并更新所有受影响层的前向指针
- 如果新节点的层数高于当前跳表的层数,则更新跳表的层数
插入操作的平均时间复杂度为O(log n),因为查找位置的时间复杂度是O(log n),而更新指针的操作是O(L),其中L是新节点的层数,平均为常数。
删除操作
示例代码
跳表的删除过程与插入类似:
- 搜索目标节点,同时记录每一层需要更新的节点
- 找到目标节点后,更新所有受影响的前向指针
- 如果删除后某层变为空,则减少跳表的层数
public boolean delete(int key) {
// 创建更新数组
SkipListNode[] update = new SkipListNode[MAX_LEVEL + 1];
SkipListNode current = this.header;
// 从最高层开始,查找目标节点
for (int i = this.level; i >= 0; i--) {
while (current.forward[i] != null && current.forward[i].key < key) {
current = current.forward[i];
}
update[i] = current;
}
// 移动到下一节点
current = current.forward[0];
// 如果找到目标节点
if (current == null || current.key != key) {
return false;
}
//从最基层开始,更新所有收到影响层的前向指针
for (int i = 0; i <= this.level; i++) {
if (update[i].forward[i] != current) {
break;
}
update[i].forward[i] = current.forward[i];
}
// 删除没有元素的层
while (this.level > 0 && this.header.forward[this.level] == null) {
this.level--;
}
return true;//没有找到目标节点
}
删除步骤
如下是删除值为12的节点的过程。删除操作包括查找目标节点、记录更新路径和更新指针。
步骤一 查找目标节点并记录更新路径:
- 我们要删除值为12的节点。首先需要从最高层开始,找到目标节点,并记录每层需要更新的节点(前驱节点)。
- 当前位置:Level 2的Head节点
- 目标:找到值为12的节点并记录每层的前驱节点

步骤二**Level 2层搜索**:
- 在Level 2层,当前位置是节点7。其下一个节点是18,因为18 > 12,所以我们不能继续向右移动。记录节点7为Level 2层需要更新的节点。
- 当前位置:Level 2的节点7
- 判断:下一个节点18 > 12,无法继续右移,记录update[2] = 7
- 降级到Level 1继续搜索
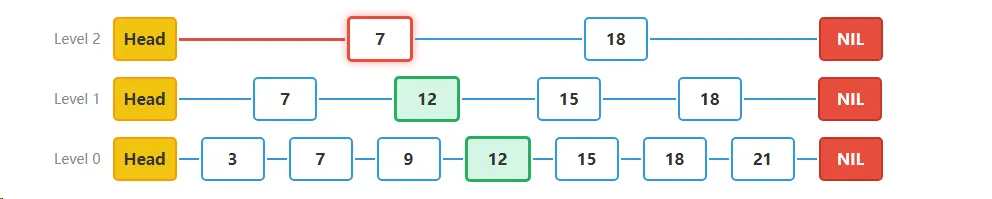
步骤三**Level 1层搜索**:
- 在Level 1层,当前位置是节点7。下一个节点是12,因为12 = 12,我们找到了目标节点的前驱节点。记录节点7为Level 1层需要更新的节点。
- 当前位置:Level 1的节点7
- 判断:下一个节点12 = 12(是目标节点),记录update[1] = 7
- 降级到Level 0继续搜索

步骤四Level 0层搜索:
- 在Level 0层,我们移动到节点9。下一个节点是12,因为12 = 12,我们找到了目标节点的前驱节点。记录节点9为Level 0层需要更新的节点。
- 当前位置:Level 0的节点9
- 判断:下一个节点12 = 12(是目标节点),记录update[0] = 9
- 此时我们已经找到了每一层需要更新的节点:
- Level 2: 节点7(虽然Level 2没有节点12,但为了完整性记录前驱)
- Level 1: 节点7
- Level 0: 节点9
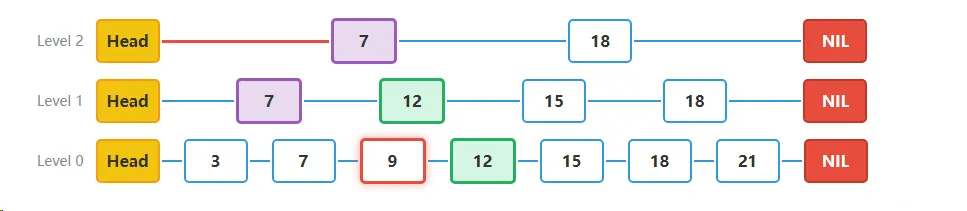
步骤五**更新Level 0层的指针**:
- 找到目标节点12后,我们开始更新指针。首先更新Level 0层的指针:
- 节点9的next指向原来12节点指向的15节点
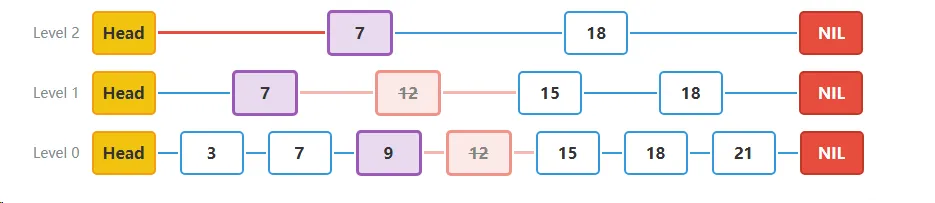
步骤六**更新Level 1层的指针**:
- 继续更新Level 1层的指针:
- 节点7的next指向原来12节点指向的15节点
- Level 2层没有节点12,所以无需更新。
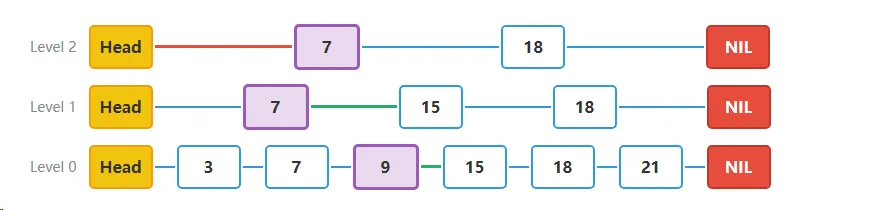
步骤七**删除完成**:
- 删除操作完成,节点12已从跳表中移除。所有相关的指针都已更新,跳表的结构保持有序。
- 结果:
- 节点12已从Level 0和Level 1层移除
- 所有相关的指针都已更新
- 跳表的结构保持完整和有序
删除操作总结:
- 首先从最高层开始,查找目标节点,并记录每一层需要更新的节点(前驱节点)
- 检查目标节点是否存在于跳表中,如果不存在则删除失败
- 如果找到目标节点,从底层开始,更新所有受影响层的前向指针
- 检查并删除没有元素的最高层
删除操作的平均时间复杂度为O(log n),因为查找节点的时间复杂度是O(log n),而更新指针的操作与节点的层数相关,平均为常数。
复杂度分析
时间复杂度
跳表的主要操作时间复杂度如下:
| 操作 | 平均时间复杂度 | 最坏时间复杂度 |
|---|---|---|
| 查找 | O(log n) | O(n) |
| 插入 | O(log n) | O(n) |
| 删除 | O(log n) | O(n) |
跳表的平均时间复杂度为O(log n)的原因:
- 在查找过程中,每一层都大约跳过一半的节点
- 跳表的层数平均为O(log n)
- 在每一层最多访问O(1)个节点
空间复杂度
跳表的空间复杂度为O(n),其中n是元素个数。虽然跳表有多层,但总的额外空间消耗仍然是有界的:
- 第0层:n个节点
- 第1层:约n/2个节点
- 第2层:约n/4个节点
- …
- 总节点数约为:n + n/2 + n/4 + … ≈ 2n
因此,额外空间消耗的常数因子通常小于2。
完整代码
package lianbiao;
import java.util.*;
/**
* @Author Stringzhua
* @Date 2025/10/23 17:35
* description:跳表
*/
/**
* 跳表节点类
*/
class SkipListNode {
Integer key;
SkipListNode[] forward;
public SkipListNode(Integer key, int level) {
this.key = key;
this.forward = new SkipListNode[level + 1];
}
@Override
public String toString() {
return "SkipListNode(key=" + key + ")";
}
}
/**
* 跳表实现类
*/
class SkipList implements Iterable<Integer> { // 实现Iterable接口
private static final int MAX_LEVEL = 16;
private static final double P = 0.5;
private int level;
private SkipListNode header;
private Random random;
public SkipList() {
this.level = 0;
this.header = new SkipListNode(null, MAX_LEVEL);
this.random = new Random();
}
// 新增:获取当前跳表最大层数(供外部范围查询使用)
public int getLevel() {
return this.level;
}
// 新增:获取头节点(供外部范围查询使用)
public SkipListNode getHeader() {
return this.header;
}
private int randomLevel() {
int level = 0;
while (random.nextDouble() < P && level < MAX_LEVEL) {
level++;
}
return level;
}
public SkipListNode search(int key) {
SkipListNode current = this.header;
//从最高层开始,逐层向下查找
for (int i = this.level; i >= 0; i--) {
//在当前层水平移动,知道找到小于或等于目标值的最大节点
while (current.forward[i] != null && current.forward[i].key < key) {
current = current.forward[i];
}
}
//现在在底层,检查下一个节点是否是目标值
current = current.forward[0];
//如果下个节点存在并且key相等,则找到目标
if (current != null && current.key == key) {
return current;
}
return null;//未找到目标
}
public boolean insert(int key) {
// 创建更新数组,用于存储需要更新前向指针的节点
SkipListNode[] update = new SkipListNode[MAX_LEVEL + 1];
SkipListNode current = this.header;
// 从最高层开始,查找适合的插入位置
for (int i = this.level; i >= 0; i--) {
while (current.forward[i] != null && current.forward[i].key < key) {
current = current.forward[i];
}
// 记录每一层需要更新的节点
update[i] = current;
}
// 移动到下一个节点
current = current.forward[0];
// 检查key是否已经存在
if (current != null && current.key == key) {
return false;// key已存在,则插入失败
}
// 为新节点生成随机层数
int randomLevel = randomLevel();
if (randomLevel > this.level) {
// 更新跳表当前最大层数
for (int i = this.level + 1; i <= randomLevel; i++) {
update[i] = this.header;
}
this.level = randomLevel;
}
// 创建新的节点
SkipListNode newNode = new SkipListNode(key, randomLevel);
// 更新所有受影响的前向指针
for (int i = 0; i <= randomLevel; i++) {
newNode.forward[i] = update[i].forward[i];
update[i].forward[i] = newNode;
}
return true;
}
public boolean delete(int key) {
// 创建更新数组
SkipListNode[] update = new SkipListNode[MAX_LEVEL + 1];
SkipListNode current = this.header;
// 从最高层开始,查找目标节点
for (int i = this.level; i >= 0; i--) {
while (current.forward[i] != null && current.forward[i].key < key) {
current = current.forward[i];
}
update[i] = current;
}
// 移动到下一节点
current = current.forward[0];
// 如果找到目标节点
if (current == null || current.key != key) {
return false;
}
//从最基层开始,更新所有收到影响层的前向指针
for (int i = 0; i <= this.level; i++) {
if (update[i].forward[i] != current) {
break;
}
update[i].forward[i] = current.forward[i];
}
// 删除没有元素的层
while (this.level > 0 && this.header.forward[this.level] == null) {
this.level--;
}
return true;//没有找到目标节点
}
public void display() {
for (int i = this.level; i >= 0; i--) {
System.out.print("Level " + i + ": ");
SkipListNode node = this.header.forward[i];
while (node != null) {
System.out.print(node.key + " -> ");
node = node.forward[i];
}
System.out.println("null");
}
}
/**
* 实现Iterable接口的iterator()方法
*/
@Override
public Iterator<Integer> iterator() {
return new Iterator<Integer>() {
private SkipListNode current = header.forward[0];
@Override
public boolean hasNext() {
return current != null;
}
@Override
public Integer next() {
if (!hasNext()) {
throw new NoSuchElementException();
}
int key = current.key;
current = current.forward[0];
return key;
}
};
}
public boolean contains(int key) {
return search(key) != null;
}
public int size() {
int count = 0;
SkipListNode current = header.forward[0];
while (current != null) {
count++;
current = current.forward[0];
}
return count;
}
}
/**
* 跳表功能测试类
*/
public class SkipListDemo {
public static void basicOperationsDemo() {
System.out.println("=== 基本操作演示 ===");
SkipList skipList = new SkipList();
System.out.println("\n插入元素:");
int[] elements = {3, 6, 7, 9, 12, 19, 17, 26, 21, 25};
for (int elem : elements) {
skipList.insert(elem);
System.out.println("插入 " + elem);
}
System.out.println("\n跳表结构:");
skipList.display();
System.out.println("\n搜索元素:");
int[] searchElements = {7, 12, 19, 25, 30};
for (int elem : searchElements) {
boolean exists = skipList.contains(elem);
System.out.println("搜索 " + elem + ": " + (exists ? "存在" : "不存在"));
}
System.out.println("\n删除元素:");
int[] deleteElements = {7, 12, 30};
for (int elem : deleteElements) {
boolean success = skipList.delete(elem);
System.out.println("删除 " + elem + ": " + (success ? "成功" : "失败"));
}
System.out.println("\n删除后的跳表结构:");
skipList.display();
// 修复2:现在支持for-each遍历(因SkipList实现了Iterable接口)
System.out.println("\n遍历所有元素:");
List<Integer> allElements = new ArrayList<>();
for (int key : skipList) {
allElements.add(key);
}
System.out.println(allElements);
}
public static void performanceTest(int n) {
System.out.println("\n=== 性能测试 ===");
SkipList skipList = new SkipList();
List<Integer> data = new ArrayList<>();
for (int i = 0; i < n; i++) {
data.add(i);
}
Collections.shuffle(data);
List<Integer> testSample = data.subList(0, 100);
System.out.println("\n插入 " + n + " 个元素:");
long startTime = System.nanoTime();
for (int key : data) {
skipList.insert(key);
}
long endTime = System.nanoTime();
double cost = (endTime - startTime) / 1e6;
System.out.printf("耗时: %.6f 秒%n", cost / 1000);
System.out.println("\n搜索 100 个元素:");
startTime = System.nanoTime();
for (int key : testSample) {
skipList.search(key);
}
endTime = System.nanoTime();
cost = (endTime - startTime) / 1e6;
System.out.printf("耗时: %.6f 秒%n", cost / 1000);
System.out.println("\n删除 100 个元素:");
startTime = System.nanoTime();
for (int key : testSample) {
skipList.delete(key);
}
endTime = System.nanoTime();
cost = (endTime - startTime) / 1e6;
System.out.printf("耗时: %.6f 秒%n", cost / 1000);
}
public static void rangeQueryExample() {
System.out.println("\n=== 范围查询示例 ===");
SkipList skipList = new SkipList();
for (int i = 1; i <= 100; i++) {
skipList.insert(i);
}
class RangeQuery {
List<Integer> query(SkipList skipList, int start, int end) {
List<Integer> result = new ArrayList<>();
// 修复3:通过getter获取private成员(header和level)
SkipListNode header = skipList.getHeader();
int currentLevel = skipList.getLevel();
// 从最高层向下查找起始位置
SkipListNode current = header;
for (int i = currentLevel; i >= 0; i--) {
while (current.forward[i] != null && current.forward[i].key < start) {
current = current.forward[i];
}
}
// 收集范围内的元素
current = current.forward[0];
while (current != null && current.key <= end) {
result.add(current.key);
current = current.forward[0];
}
return result;
}
}
RangeQuery rangeQuery = new RangeQuery();
int[][] ranges = {{10, 20}, {50, 60}, {95, 105}};
for (int[] range : ranges) {
int start = range[0];
int end = range[1];
List<Integer> result = rangeQuery.query(skipList, start, end);
System.out.println("范围 [" + start + ", " + end + "] 内的元素: " + result);
}
}
public static void main(String[] args) {
basicOperationsDemo();
performanceTest(10000);
rangeQueryExample();
}
}























 1554
1554

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








