作者分享了2022年蓝桥杯的经历，强调了官方对防止作弊的措施。重点解析了九进制转十进制、顺子日期问题，以及C/C++代码优化。提到刷题统计部分，包括了两个C++代码片段及其优化过程，涉及进制运算和前缀和计算。
2022.04.09，我第一次参加蓝桥杯，我想说今年官方为了防止作弊，可谓煞费苦心，直接启用备用卷，难度直接到国赛难度。第一次参加，却让我输的那么彻底。
2023.04.05更新了题解，祝各位在4.8能取得一个圆满的成绩！
目录
A九进制转十进制
答案：1478
B 顺子日期
答案：4 / 14
解析：我填了4，当时我一直在想012算不算，题目说了20220123有一个顺子：123，没说是012，所以我认定它不算，那就只有20220123，20221123，20221230，20221231。注意：降序是不算顺子的。
C 刷题统计
for（50分吧）
#include <bits/stdc++.h>
#define MOD 1000000007
using namespace std;
typedef long long LL;
LL a,b,n;
int main() {
int sum=0;
cin>>a>>b>>n;
for(LL i=1; ;i++) {
if(i%7!=6 && i%7!=0) sum+=a;
else sum+=b;
if(sum>=n) {
cout<<i;
return 0;
}
}
return 0;
}优化（应该100）
#include <bits/stdc++.h>
#define MOD 1000000007
using namespace std;
typedef long long LL;
LL a,b,n;
int main() {
cin>>a>>b>>n;
LL sum=a*5+b*2;//一周的做题数
LL t=n/sum;//需要t周（往下取整）
LL nn=t*sum;//t周做了nn个题目
if(nn>=n) cout<<t*7;
else if(nn+a>=n) cout<<t*7+1;
else if(nn+a*2>=n) cout<<t*7+2;
else if(nn+a*3>=n) cout<<t*7+3;
else if(nn+a*4>=n) cout<<t*7+4;
else if(nn+a*5>=n) cout<<t*7+5;
else if(nn+a*5+b>=n) cout<<t*7+6;
else if(nn+a*5+b*2>=n) cout<<t*7+7;//考试时没写这句，刚刚试数据查到错的....彻底无语，大无语事件
return 0;
}D 修剪灌木
解析：我是直接用草稿纸手推出来，发现的规律，1需要特判：1。2输出2 2，3输出4 2 4，4输出6 4 4 6，5输出8 6 4 6 8……以此类推就好了，我们看到边界是最高的，然后往中间成以公差为-2递减。所以用双指针控制它即可
#include <bits/stdc++.h>
#define MOD 1000000007
using namespace std;
typedef long long LL;
int a[10005];
int n;
int main() {
cin>>n;
if(n==1) {
cout<<1;
return 0;
}
int s=(n-1)*2;
int l=1,r=n;
while(l<=r) {
a[l]=a[r]=s;
l++,r--;
s-=2;
}
for(int i=1; i<=n; i++)
cout<<a[i]<<endl;
return 0;
}E X进制减法
我在考场上看到好多人卡这题，主要是读不懂题，出考场时有很多人问我321怎么等于65，题目说了三个位的进制分别是8 10 2（从左到右），所以就是3 * 20 + 2 * 2 + 1 = 65，看不懂的小伙伴可以回去好好复习一下二进制或者往下看。
解析：
321的“1”是2进制，逢2进1，即“2”就意味着数字4=2*2，“2”的进制是10进制，逢10进1，也就是说对于“2”来说，“3”代表着30，而对于“1”来说“3”则代表着60=30*2。通俗的说，假如321整个树是10进制，那么对于“2”而言“3”是30，对于“1”而言，“3”是300=3*10*10.
然后，这里的最高位进制是没用的，相当于摆设。由于它说a b同一条进制系统，所以数位的进制应该是一样的，那么我们就需要一个s数组来存放当前数位应该*哪个数了
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5+10, mod=1000000007;
typedef long long LL;
LL a[N], b[N],res;
int n,ma,mb;
int main()
{
cin>>n;
cin>>ma;
for(int i=ma-1; i>=0; i--) cin>>a[i];
cin>>mb;
for(int i=mb-1; i>=0; i--) cin>>b[i];
for(int i=max(ma,mb)-1; i>=0; i--)
{
LL h=max(a[i]+1ll, max(b[i]+1ll, 2ll));
res=(res*h%mod+(LL)(a[i]-b[i]))%mod;
}
cout<<res;
return 0;
}F 统计子矩阵
二维前缀和，不会。。。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 510;
int s[N][N];
int n,m,k;
LL res;
int main()
{
scanf("%d%d%d",&n,&m,&k);
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
{
scanf("%d",&s[i][j]);
s[i][j]+=s[i-1][j];
}
for(int i=1; i<=n; i++)
for(int j=i; j<=n; j++)
for(int l=1,r=1,sum=0; r<=m; r++)
{
sum+=s[j][r]-s[i-1][r];
while(sum>k)
{
sum-=s[j][l]-s[i-1][l];
l++;
}
res=(LL)res+r-l+1;
}
cout<<res;
return 0;
}G 积木画
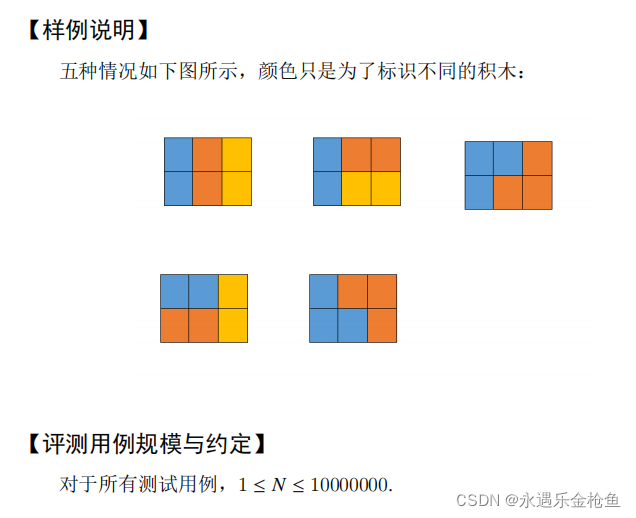
听他们说这道题在洛谷有原题，而且是用dp做，完全和他们不一样，我用斐波那契做的
解析：
这题我依旧是手推找规律。
n为1时是1 = 1 + 0 * 2；
n为2时是2 = 2 + 0 * 2;
n为3时是5 = 3 + 1 * 2;
n为4时是9 = 5 + 2 * 2;
n为5时是18 = 8 + 5 * 2;
n为6时是35 = 13 + 12 * 2;
n为7时是67 = 21 + 23 * 2;以此类推
我们发现前面的（只有I形）是斐波那契数列，后面的（有L和I型）是一个有规律的数列吧，我也不知道啥数列：2 + 3 = 5，5 + 6 = 11，11 + 12 = 23
我也不知道对不对，没管后面了，直接编程交了，然后看了一下洛谷的，发现错了。
代码就不给了，这个是错误思路，正解请移步洛谷P1990
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e7+10, mod=1000000007;
typedef long long LL;
LL f[N];
int n;
int main()
{
cin>>n;
f[1]=1;
f[2]=2;
f[3]=5;
for(int i=4; i<=n; i++)
f[i]=(2*f[i-1]%mod+f[i-3])%mod;
cout<<f[n];
return 0;
}H 扫雷
这个我好像用两个for，不知道能不能骗分，听一个小伙伴说是0分，那太好了，又错了.......
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 50010, M=999997;
LL h[M]; //哈希值
bool st[M]; //标记当前坑位是否被用过
int id[M]; //坑位对应的最大半径的炸雷的编号
int n,m;
//存储炸雷
struct circle
{
int x,y,r;
}cir[N];
//把x和y合并起来
LL get_key(int x,int y)
{
return x*1000000001ll+y;
}
//找坑位
int find(int x,int y)
{
LL key=get_key(x,y);
int t=(key%M+M)%M;
//空坑位或者找到目标点
while(h[t]!=-1 && h[t]!=key)
if(++ t==M) t=0;
return t;
}
int sqr(int x)
{
return x*x;
}
void dfs(int x,int y,int r)
{
st[find(x,y)]=true;
for(int i=x-r; i<=x+r; i++)
for(int j=y-r; j<=y+r; j++)
{
if(sqr(i-x)+sqr(j-y)<=sqr(r))
{
int t=find(i,j);
if(!st[t] && id[t])
dfs(i,j,cir[id[t]].r);
}
}
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
for(int i=1; i<=n; i++)
{
int x,y,r;
scanf("%d%d%d",&x,&y,&r);
cir[i]={x,y,r};
int t=find(x,y); //找到对应的坑位
if(h[t]==-1) h[t]=get_key(x,y); //坑位对应一个哈希值
if(!id[t] || cir[id[t]].r < r) id[t]=i;
}
//遍历导弹
while (m -- )
{
int x,y,r;
scanf("%d%d%d",&x,&y,&r);
for(int i=x-r; i<=x+r; i++)
for(int j=y-r; j<=y+r; j++)
{
if(sqr(i-x)+sqr(j-y)<=sqr(r))
{
int t=find(i,j);
//当前位置有雷且未被遍历
if(!st[t] && id[t])
dfs(i,j,cir[id[t]].r);
}
}
}
int res=0;
for(int i=1; i<=n; i++)
if(st[find(cir[i].x, cir[i].y)]) res++;
cout<<res;
return 0;
}I 李白打酒加强版
dfs能骗分，考的时候没想出来
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 105, mod=1000000007;
typedef long long LL;
int n,m,res;
LL f[N][N][N]; //店 花 酒
int main()
{
cin>>n>>m;
f[0][0][2]=1;
for(int i=0; i<=n; i++)
for(int j=0; j<=m; j++)
for(int k=0; k<=m; k++)
{
if(i && k%2==0) f[i][j][k]=(f[i-1][j][k/2]+f[i][j][k])%mod;
if(j && k>0) f[i][j][k]=(f[i][j-1][k+1]+f[i][j][k])%mod;
}
cout<<f[n][m-1][1]; //最后一次遇花留一斗
return 0;
}J 砍竹子
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 2e5+10, M=20;
typedef long long LL;
LL f[N][M];
int n, m, res;
int main()
{
cin>>n;
for(int i=0; i<n; i++)
{
int stk[M], hh=0;
LL x;
cin>>x;
while(x>1)
{
stk[hh++]=x;
x=sqrtl(x/2+1);
res++;
}
m=max(m,hh);
for(int j=0; j<hh; j++)
f[i][j]=stk[hh-j-1];
}
for(int i=0; i<m; i++)
for(int j=1; j<n; j++)
if(f[j][i]==f[j-1][i] && f[j][i])
res--;
cout<<res;
return 0;
}
这次顶死40分，没省二咯，该退役咯~~~
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
