第五章 动态规划（二）——线性dp与区间dp

线性dp

898. 数字三角形

898. 数字三角形 - AcWing题库

状态表示：

• 集合：数字三角形中的所有路径，用两个维度限制路径的终点，$f(i,j)$表示从起点走到$(i,j)$的所有路径
• 属性：所有路径中的数字和最大值
  最终$f(i,j)$就表示从起点走到$(i,j)$这个点的数字和最大值

状态计算：集合划分，思考$f(i,j)$这个集合如何划分？
根据题意，从起点到$(i,j)$必定经过$(i-1,j-1)$与$(i-1,j)$这两个点，$f(i,j)$中的所有路径和一定会加上$(i,j)$这个点上的数字，所以路径和的最大值减去这个数字也不影响它是最大值。此时集合就被划分成了$f(i-1,j-1)$与$f(i-1,j)$，从两者中取较大值，加上点$(i,j)$的数字得到$f(i,j)$
即$f(i,j)=max(f(i-1,j-1),f(i-1,j))+a[i][j]$

tips：若涉及到i-1这样的状态，那么下标从1开始，设置0下标为初始值

#include <iostream>
#include <cstring>
using namespace std;

const int N = 510, INF = 1e9 + 7;
int a[N][N], f[N][N];

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++ i )
        for (int j = 1; j <= i; ++ j )
            scanf("%d", &a[i][j]);
            
    for (int i = 0; i <= n; ++ i )
        for (int j = 0; j <= i + 1; ++ j )
            f[i][j] = -INF;
    f[1][1] = a[1][1];
    
    for (int i = 2; i <= n; ++ i )
        for (int j = 1; j <= i; ++ j)
            f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
    
    int res = -INF;
    for (int j = 1; j <= n; ++ j) res = max(res, f[n][j]);
    
    printf("%d", res);
    return 0;
}

需要注意边界情况，由于我们从1下标开始使用a数组，那么a数组的0行0列都没有使用，此时将它们初始化成-INF，不会影响答案
此外由于$(i,j)$的更新需要用到$(i-1,j)$，比如$(3,3)$要用到$(2,3)$，这个状态不存在，也需要设置为-INF

---

895. 最长上升子序列

895. 最长上升子序列 - AcWing题库

计算最长上升子序列的长度
状态表示：

• 集合：题目给定的序列中，所有的上升子序列。假设序列的长度为n，用序列以第i个数结尾限制集合，其中$1<=i<=n$
• 属性：最大上升子序列长度
  所以$f(i)$表示：题目给定的序列中，以第$i$个数结尾的最长子序列

状态计算：
如何划分$f(i)$这个集合？从序列的角度考虑，以第$i$个数结尾的序列，倒数第二个数可能是什么？第$1,2,...,i-1$个数，以这些数结尾的序列为$f(1),f(2),...,f(i-1)$，将这些序列加上a[i]就能得到$f(i)$，所以，这些集合不重不漏组成集合$f(i)$
由于题目要求的子序列是上升的，因此子序列$f(1),f(2),...,f(i-1)$的最后一个数小于第i个数，才能构成上升序列
即a[j] < a[i]时，有$f(i)=max(f(i),f(j)+1)$

思考$f(i)$的初始状态，最坏情况下，最长上升子序列就是自己，长度为1，即$f(i)=1$

#include <iostream>
using namespace std;

const int N = 1010;
int a[N], f[N];

int main()
{
    int res = 1, n;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++ i ) scanf("%d", &a[i]), f[i] = 1;
    
    for (int i = 2; i <= n; ++ i)
        for (int j = 1; j < i; ++ j )
            if (a[j] < a[i]) 
            {
                f[i] = max(f[i], f[j] + 1);
                res = max(res, f[i]);
            }
                
    printf("%d", res);
    
    return 0;
}

若题目要求打印最长上升子序列，我们需要额外记录当前状态是从哪个状态更新来的

#include <iostream>
using namespace std;

const int N = 1010;
int a[N], f[N], p[N];

void out(int k)
{
    if (p[k] != 0) out(p[k]);
    printf("%d ", a[k]);
}

int main()
{
    int res = 1, n;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++ i ) scanf("%d", &a[i]), f[i] = 1;
    
    for (int i = 2; i <= n; ++ i)
        for (int j = 1; j < i; ++ j )
            if (a[j] < a[i]) 
            {
                if (f[j] + 1 > f[i])
                {
                    f[i] = f[j] + 1;
                    p[i] = j;
                    res = max(res, f[i]);
                }
            }
    
    int k = 1;
    while (f[k] != res) k ++ ;
    out(k);
    
    return 0;
}

---

897. 最长公共子序列

897. 最长公共子序列 - AcWing题库

求出现在$a$序列以及$b$序列中的最长公共子序列长度

状态表示：

• 集合：所有公共子序列，用两个维度限制这些子序列。在$a$序列的前$i$个字符中出现的子序列同时也在 $b$序列的前$j$个字符中出现
• 属性：所有公共子序列中，最长的子序列长度
  $f(i,j)$表示在$a$序列的前$i$个字符中出现，同时也在$b$序列的前$j$个字符中出现的最长子序列

状态计算：如何划分$f(i,j)$这个集合？根据公共子序列是否包含$a[i]，b[i]$划分成四种情况。也就是公共子序列的最后一个字符是否是$a[i]$，$b[j]$

• 00：公共子序列不包含两者（此时$a[i]!=b[j]$）
• 11：公共子序列包含两者（此时$a[i]=b[j]$）
• 01：公共子序列不包含$a[i]$但包含$b[i]$（此时$a[i]!=b[j]$）
• 10：公共子序列包含$a[i]$但不包含$b[i]$（此时$a[i]!=b[j]$）

00用$f(i-1,j-1)$表示：在$a$序列的前$i-1$个字符出现并且在$b$序列的前$j-1$个字符中出现的子序列，此时这些子序列一定不包含$a[i]，b[j]$
11用$f(i-1,j-1)+1$表示：由于子序列包含两者($a[i]=b[j]$)，所以子序列的最后一个字符一定是$a[i]（b[j]）$。删除这个字符，此时的状态为$f(i-1,j-1)$，$f(i,j)$最长公共序列长度需要在此基础上+1
01用$f(i-1,j)$表示：在$a$序列的前$i-1$个字符出现并且在$b$序列的前$j$个字符中出现的子序列，注意：01是$f(i-1,j)$的子集，因为$f(i-1,j)$中，只有部分子序列是以$b[j]$结尾的
10用$f(i,j-1)$表示：在$a$序列的前$i$个字符出现并且在$b$序列的前$j-1$个字符中出现的子序列，注意：10是$f(i,j-1)$的子集，因为$f(i,j-1)$中，只有部分子序列是以$a[i]$结尾的

虽然$00,11,01,10$这四个集合能够不重不漏的组成$f(i,j)$，但是这四个集合转换后的f状态不能不重不漏组成$f(i,j)$，因为01和10的f状态不够准确
虽然01和10的f状态不准确，但是两者的最长公共子序列是相同的，所以取max之后两者是等价的
并且$f(i-1,j)$和$f(i,j-1)$取max后的结果 >= $f(i-1,j-1)$，所以不用特别的对$f(i-1,j-1)$取max

#include <iostream>
using namespace std;

const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];

int main()
{
    scanf("%d%d", &n, &m);
    scanf("%s%s", a + 1, b + 1);
    
    for (int i = 1; i <= n; ++ i )
        for (int j = 1; j <= m; ++ j )
        {
            f[i][j] = max(f[i - 1][j], f[i][j - 1]);
            if (a[i] == b[j]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
        }
        
    printf("%d\n", f[n][m]);
    return 0;
}

---

区间dp

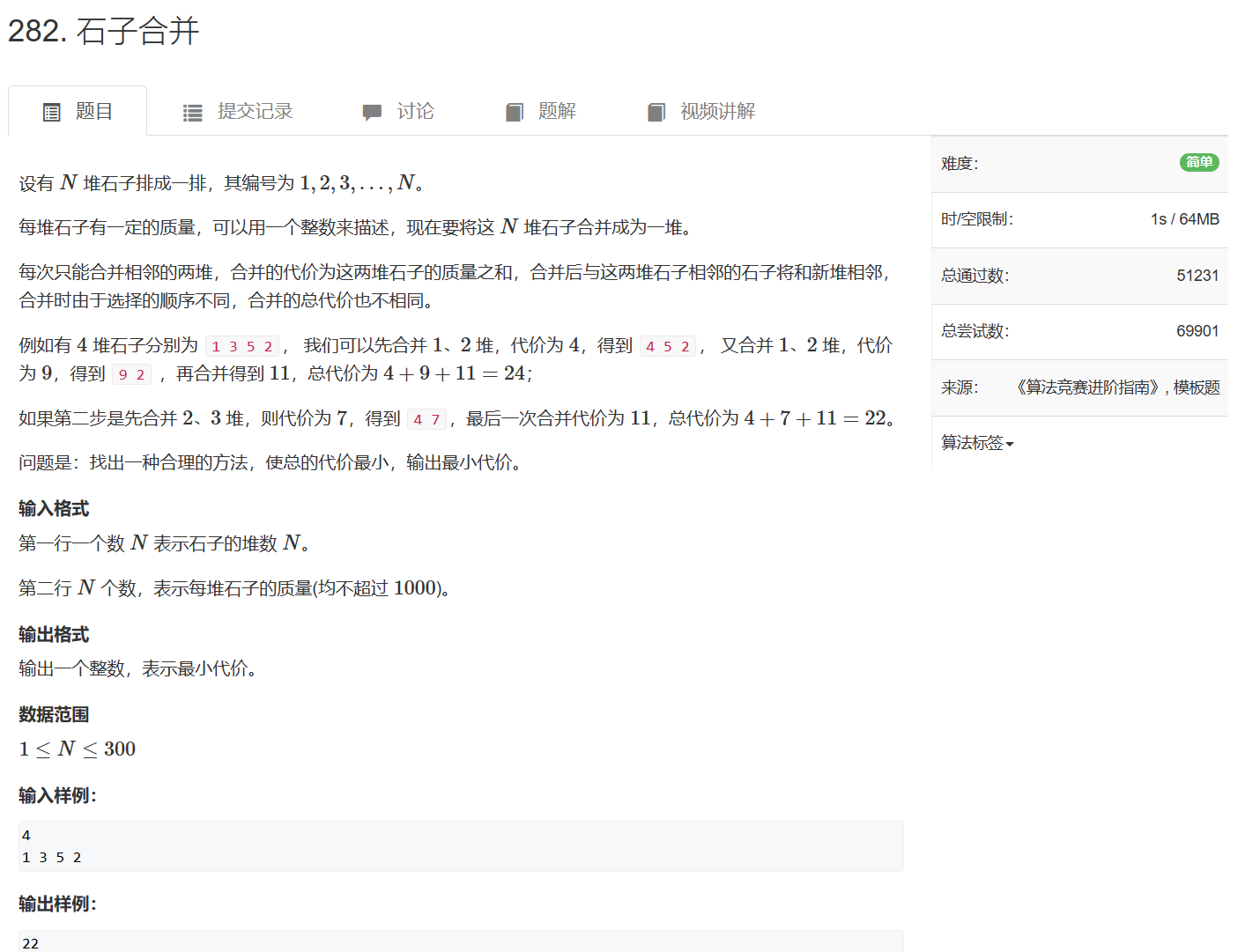
282. 石子合并

282. 石子合并 - AcWing题库

状态表示：

• 集合：对于给定的石子，所有的合并方法。用两个维度限制集合中的元素——合并第$i$堆石子到第$j$堆石子的方法
• 属性：所有合并方法中的最小代价
  $f(i,j)$表示合并第$i$堆石子到第$j$堆石子的最小代价

状态计算：要将一个区间内的石堆合并一堆石子，最后一步一定是将两堆石子合并成一堆，由于只能合并相邻的石堆，所以最后一步需要合并的两个石堆一定是相邻的。根据这个性质从$[i+1,j-1]$枚举两堆石子的分界点，这些情况能不重不漏的组成$f(i,j)$

再考虑状态的属性：合并石堆的最小代价。最后一步合并两堆石子的代价是$a[i],...,a[j]$的石子数累加。即，无论两堆石子是怎样合并的，这两堆石子数量相加一定等于$a[i],...,a[j]$的石子数累加。省略付出的相同代价，枚举分界点找到$f(i,k)+f(k+1,j)$的最小值即可，其中k从$(i,j-1)$

注意：区间dp与线性dp不同，线性dp一般有一个状态更新的方向，把状态抽象成n维矩阵后，这个方向是线性的
而区间dp的状态更新，需要从最小的区间开始，即，区间的长度越来越大

本题中，区间长度为1时，付出的代价为0，即，没有代价，所以从区间长度为2时开始更新
我们从2开始枚举区间长度，以第1堆石子作为左端点，根据长度得到右端点，更新该区间

#include <iostream>
using namespace std;

const int N = 310, INF = 1e9;
int f[N][N];
int s[N];

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++ i ) scanf("%d", &s[i]);
    for (int i = 1; i <= n; ++ i ) s[i] += s[i - 1]; // 前缀和数组的构造

    for (int len = 2; len <= n; ++ len )
    {
        for (int i = 1; i + len - 1 <= n; ++ i )
        {
            int l = i, r = i + len - 1;
            f[l][r] = INF;
            for (int k = l; k < r; ++ k ) // k作为分界点
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
        }
    }
    
    printf("%d\n", f[1][n]);
    
    return 0;
}

由于合并区间$[i,j]$的最后一步中，一定会付出从$a[i]$累加到$a[j]$的代价，所以这里用前缀和数组代替原数组已方便计算

---

线性dp练习题

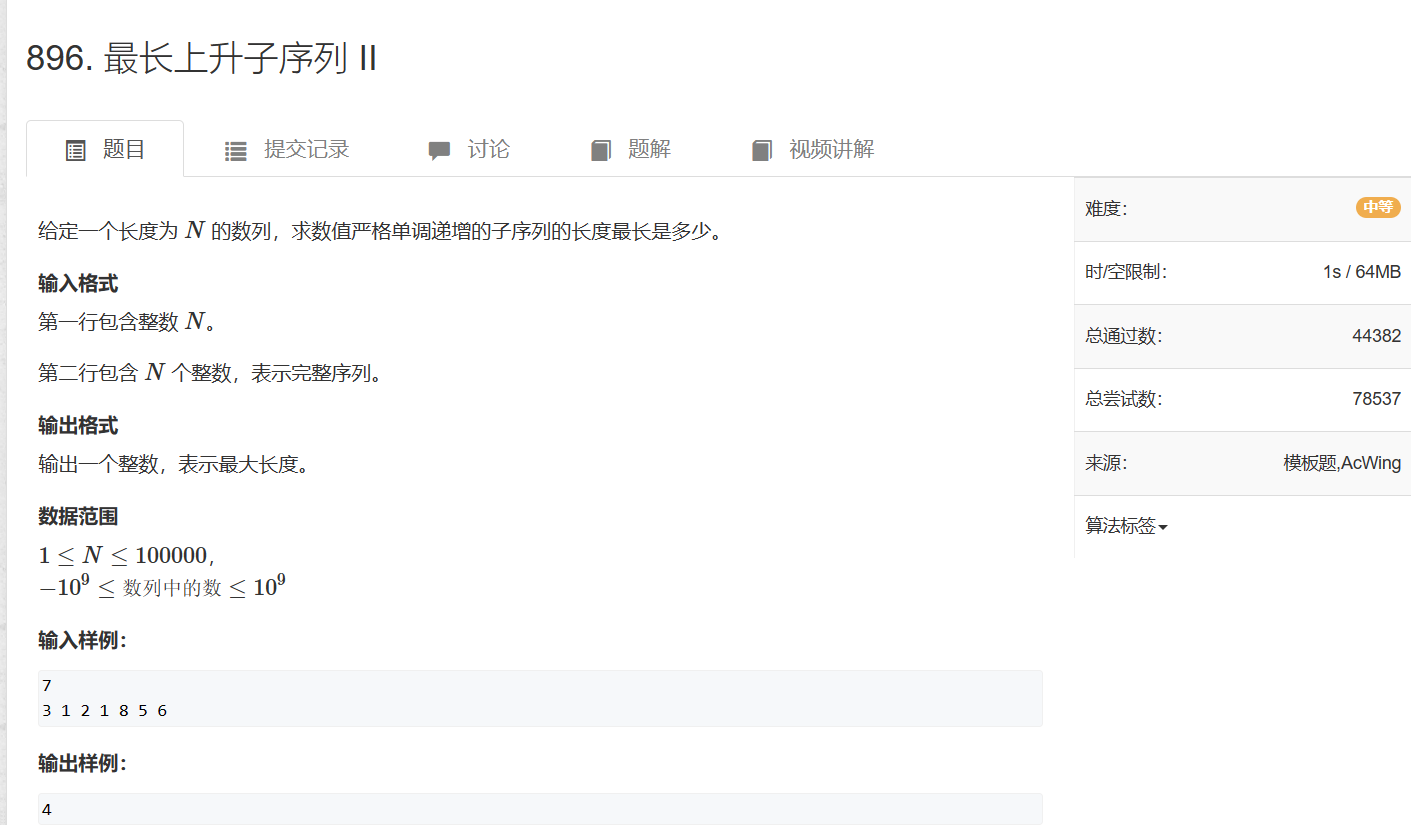
896. 最长上升子序列 II

896. 最长上升子序列 II - AcWing题库

思考算法是否存在可以优化的地方：在划分$f(i)$这个集合时，我们将$O(n)$地遍历数组中第1~i-1个数，若该数小于第i个数，则试着更新$f(i)$
若$a[j]<a[k]$，并且$a[i]>a[k]$，那么在以第i个数结尾的上升子序列中，第j个数和第k个数都能作为倒数第二个数。其中$a[j]<a[k]<a[i]$，若$a[i]$能接到$a[k]$后，那么它一定能接到$a[j]$后，因为$a[j]$比$a[k]$小
在最长上升子序列长度相等的情况下，不同的上升子序列最后一个数不同，我们只要保存这些子序列中最后一个数的最小值即可，这里有贪心的思想：长度相同的情况下，最后一个数越小，那么它后面可能接的数就越多，上升子序列的长度可能越大

同时，随着上升子序列长度的增加，最后一个数的最小值也在增加
用反证法：前提是相同长度的上升子序列，我们只保存其最后一个数的最小值
假设长度为6的上升子序列最后一个数小于等于长度为5的上升子序列的最后一个数。对于长度为6的上升子序列的倒数第二个数，其肯定小于最后一个数，那么也肯定小于长度为5的上升子序列的最后一个数。说明长度为5的上升子序列的最后一个数不是所有长度为5的上升子序列最后一个数中的最小值，与前提矛盾，所以：随着上升子序列长度的增加，最后一个数的最小值也在增加

如何求得以$a[i]$结尾的最长上升子序列长度？在这个上升子序列中，倒数第二个数一定要小于第i个数，在所有小于$a[i]$的数中（这些数都出现在第i个数之前）选择最大的数（贪心的思想），并拼接到其后面，就能得到以$a[i]$结尾的最长上升子序列
假设我们已经保存了不同长度下最长上升子序列的最小值，由于这些最小值具有单调性，所以自然地想到二分，我们能用二分找到小于$a[i]$的边界，第一个小于$a[i]$的数就是所有小于$a[i]$的数的最大值，将$a[i]$拼接到该数后面，就能得到以$a[i]$结尾的最长上升子序列
接着更新第一个大于$a[i]$的数为$a[i]$，即相同长度的上升子序列中，出现了一个结尾更小的数

#include <iostream>
using namespace std;

const int N = 1e5 + 10;
int a[N], q[N];

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++ i ) scanf("%d", &a[i]);
    int len = 0;
    q[0] = -2e9;
    for (int i = 1; i <= n; ++ i )
    {
        int l = 0, r = len;
        while (l < r)
        {
            int mid = (l + r + 1) >> 1;
            if (q[mid] < a[i]) l = mid;
            else r = mid - 1;
        }
        q[l + 1] = a[i];
        len = max(len, l + 1);
    }
    printf("%d", len);
    
    return 0;
}

---

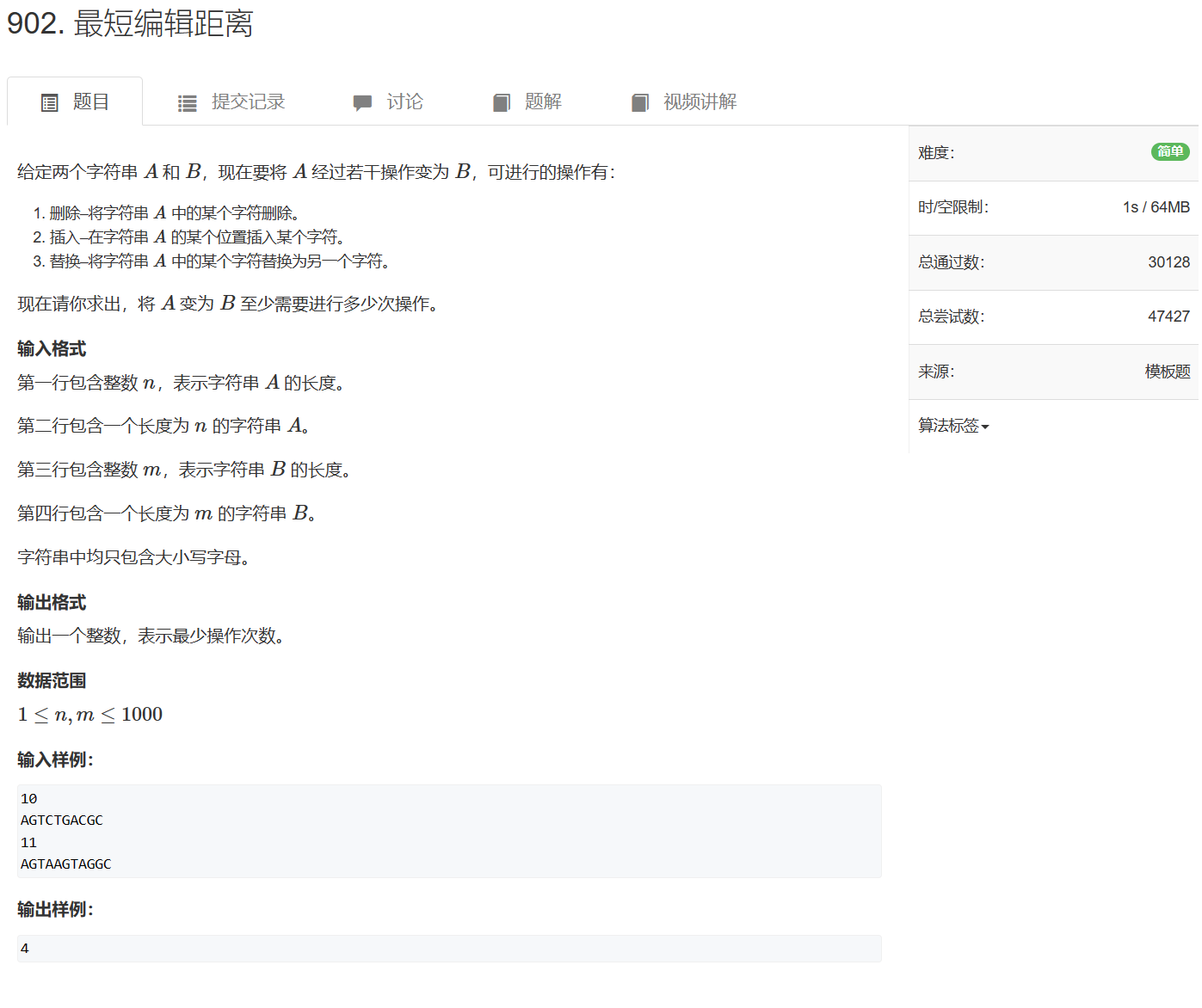
902. 最短编辑距离

902. 最短编辑距离 - AcWing题库

状态表示：
集合：所有的变换方式，用两个序列的前几个字符限制全集。即$f(i,j)$表示从A序列的前i个字符变换到B序列的前j个字符的变换方式
属性：所有变换方式中的最小变换次数
$f(i,j)$表示从A序列的前i个字符变换到B序列的前j个字符的最小变换次数

状态计算：如何划分$f(i,j)$这个集合？考虑变换的最后一步，由于变换方式有三种，所以集合能被划分成三个子集
增：在A序列的最后增加一个字符，使得A序列的前i+1个字符和B序列的前j个字符相等，此时需要保证A序列的前i个字符和B序列的前j-1个字符相等，且增加的字符为$b[j]$。集合表示为$f(i,j-1)$
删：删除A序列的最后一个字符，使得A序列的前i-1个字符和B序列的前j个字符相等，此时需要保证A序列的前i-1个字符和B序列的前j个字符相等，集合表示为$f(i-1,j)$
改：当$a[i]$与$b[j]$不同时，将$a[i]$修改为$b[j]$，此时需要保证A序列的前i-1个字符和B序列的前j-1个字符相等，集合表示为$f(i-1,j-1)$。当$a[i]$与$b[j]$相同时，不需要修改
所以$f(i,j)$就要在这三者中取最小，即$f(i, j) = min(f(i, j-1) + 1, f(i-1, j) + 1, f(i-1, j-1) + 1/0)

#include <iostream>
using namespace std;

const int N = 1010;
char a[N], b[N];
int f[N][N];

int main()
{
    int n, m;
    scanf("%d%s", &n, a + 1);
    scanf("%d%s", &m, b + 1);
    for (int i = 1; i <= n; ++ i ) f[i][0] = i;
    for (int j = 1; j <= m; ++ j ) f[0][j] = j;
    
    
    for (int i = 1; i <= n; ++ i )
        for (int j = 1; j <= m; ++ j )
        {
            if (a[i] == b[j])
                f[i][j] = min(min(f[i - 1][j] + 1, f[i][j - 1] + 1), f[i - 1][j - 1]);
            else
                f[i][j] = min(min(f[i - 1][j] + 1, f[i][j - 1] + 1), f[i - 1][j - 1] + 1);    
        }

    printf("%d", f[n][m]);
    
    return 0;
}

debug：char数组用%d读取，属于是习惯了

---

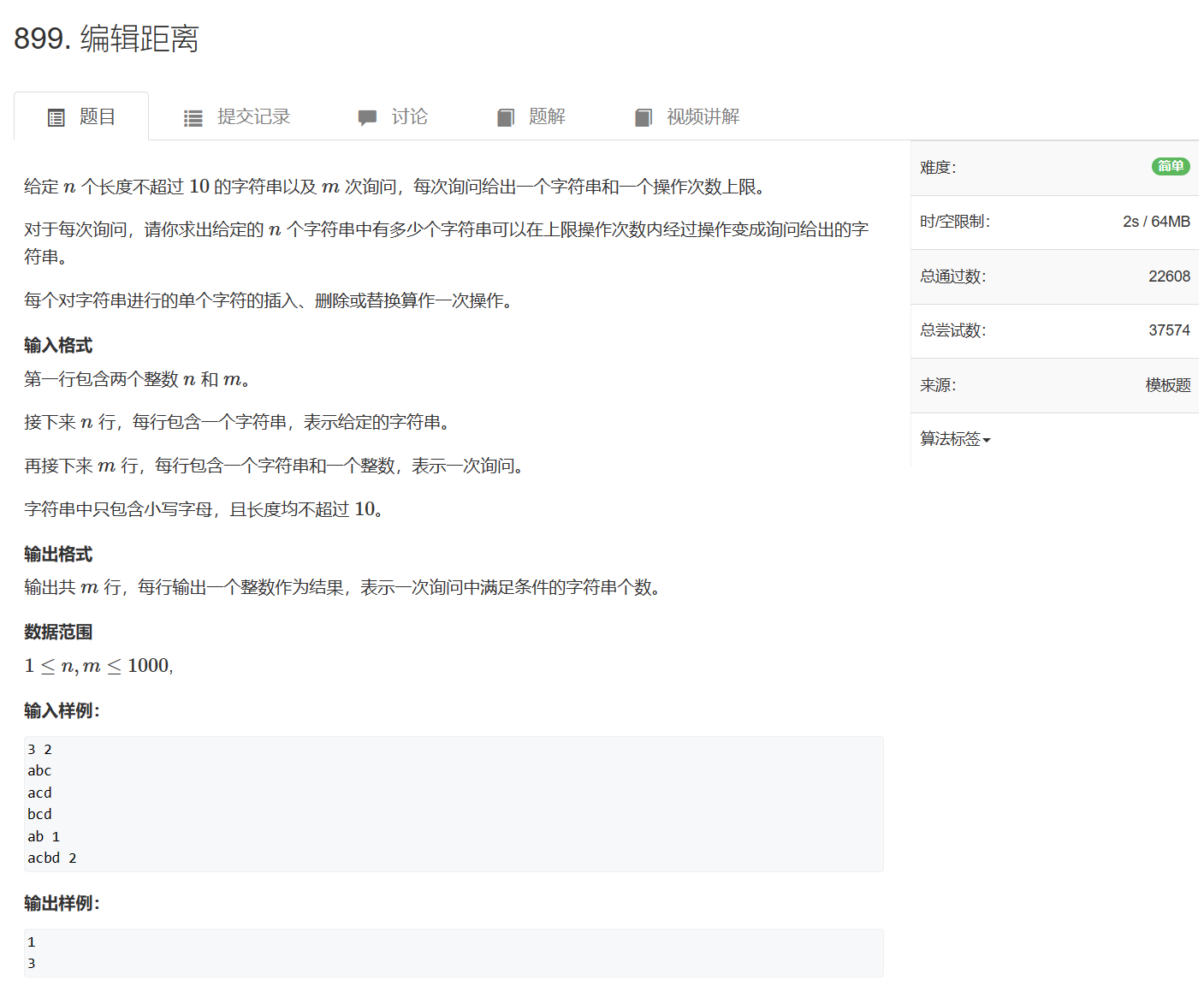
899. 编辑距离

899. 编辑距离 - AcWing题库

最短编辑距离的变形，算法都一样，处理输入输出就行

#include <iostream>
using namespace std;

const int N = 1010, L = 20;
char a[N][L], b[L];
int f[L][L];

int dis(char a[], char b[])
{
    int n, m;
    for (n = 1; a[n]; ++ n ) f[n][0] = n;
    for (m = 1; b[m]; ++ m ) f[0][m] = m;
    
    for (int i = 1; i < n; ++ i )
        for (int j = 1; j < m; ++ j )
        {
            if (a[i] == b[j])
                f[i][j] = min(f[i - 1][j] + 1, min(f[i][j - 1] + 1, f[i - 1][j - 1]));
            else
                f[i][j] = min(f[i - 1][j] + 1, min(f[i][j - 1] + 1, f[i - 1][j - 1] + 1));
        }
    return f[n - 1][m - 1];
}

int main()
{
    int n, m, lmt;
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; ++ i ) scanf("%s", a[i] + 1);
    while (m -- )
    {
        int res = 0;
        scanf("%s%d", b + 1, &lmt);
        for (int i = 0; i < n; ++ i )
            if (dis(a[i], b) <= lmt) res ++ ;
        printf("%d\n", res);
    }
    
    return 0;
}