力扣刷题记录（1）LeetCode：226、110、257

226. 翻转二叉树

这道题从整体来看确实让人有点无从下手，你要是一层一层地去看问题复杂了。这个时候需要我们从每个结点出发，单单看每个结点的话它的左右孩子就很好交换了，直接swap（root->left,root->right）。如果每个结点都进行这个操作，那翻转二叉树就完成了。

接下来就是考虑如何遍历结点，最直观也是最容易想到的就是层序遍历和递归了。其中递归又分前、中、后序遍历。但是这里中序遍历不好用。拿实例一来看，我们将2的子节点交换玩之后（先左）就是交换4的子节点了（再中），4交换完就该右节点了（再右）。这是问题就来了，4的右节点还是2，这就造成2的子节点变换了两次，7的子节点没有交换。

递归方法：

TreeNode* invertTree(TreeNode* root) {
        if(root==nullptr)   return root;
        if(root->left!=nullptr || root->right!=nullptr)
            swap(root->left,root->right);
        invertTree(root->left);
        invertTree(root->right);
        return root;
    }

层序遍历：

TreeNode* invertTree(TreeNode* root) {
        queue<TreeNode*> qu;
        int size=0;
        if(root==nullptr)   return root;
        qu.push(root);
        size++;
        while(!qu.empty())
        {
            TreeNode* temp;
            temp=qu.front();
            if(temp->left)  qu.push(temp->left);
            if(temp->right) qu.push(temp->right);
            if(temp->left!=nullptr||temp->right!=nullptr)   swap(temp->left,temp->right);
            qu.pop();
            size--;
            if(size==0)
            {
                size=qu.size();
            }
        }
        return root;
    }

110. 平衡二叉树

这里要注意是每个结点的左右子树的高度差不超过1，这就需要我们对每个结点都要进行一个相同的操作，那肯定就是要遍历每个结点了。这里我们要把每个结点都看成是一棵树，而不单单是一个结点。然后我们如果再能得出当前结点root的左右子树高度的话，那就可以直接对比两颗子树的高度差了。至于当前结点root的高度，我们只需要取root的左右子树中较大的高度再+1就是当前结点的高度了。

那现在问题就是如何求每个结点的高度了。处于最下层的高度肯定是最小的，越靠近根节点高度越大。根据这个规律我们可以从下往上一层一层地加，而恰恰后序遍历就符合这样的规律。后序遍历会访问到最底层后，再进行操作，然后一层一层返回。

class Solution {
public:
    int Height(TreeNode* root)
    {
        if(root==nullptr)   return 0;   //确定结束条件
        int leftH=Height(root->left);   //得到左子树的高度
        if(leftH==-1)    return -1;
        int rightH=Height(root->right); //得到右子树的高度
        if(rightH==-1)  return -1;
        int h=abs(leftH-rightH);        //得到左右子树的高度差
        if(h>1) return -1;              //因为一旦某个结点不是平衡二叉树那么整棵树也就不是了，-1会直接一层一层返回到根节点
        else    return max(rightH,leftH)+1; //到这一步那该结点肯定是平衡二叉树了，就将它的高度返回
    }
    bool isBalanced(TreeNode* root) {
        if(root==nullptr)   return true;    //要先判断是否为空，因为函数Height的参数不能传空值
        if(Height(root)==-1)    return false;
        return true;
    }
};

257. 二叉树的所有路径

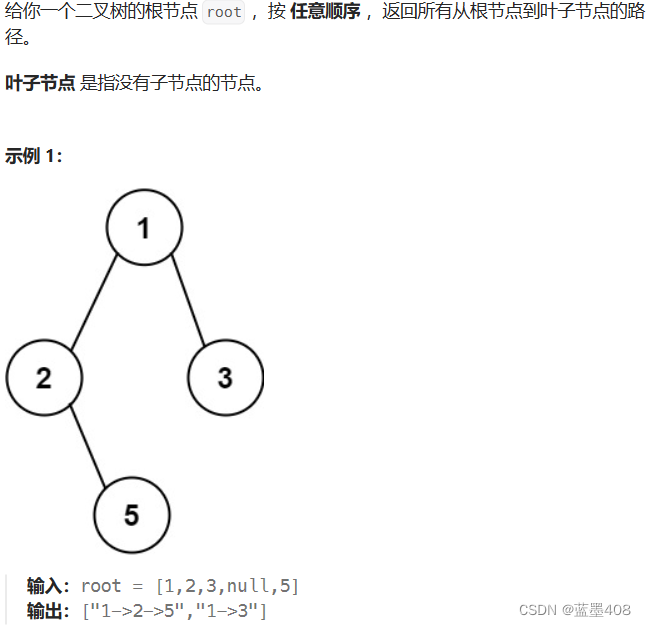
题目要求返回从根节点到叶子结点的路径，这里比较符合前序遍历。每遍历一个结点就将该结点放进一个容器中，当返回上一个结点时就将当前的节点从容器中移除。不断去维护这个容器。遇到当前结点的左右子节点为空时，就将容器中的值赋值给结果容器。前序遍历+回溯

class Solution {
public:
    vector<string> ans,temp;    //使用vector容器是因为它便于存储、移除，string操作不太方便
    void traverse(TreeNode* root)
    {
        if(root==nullptr)   return; //结束条件
        
        temp.push_back(to_string(root->val));
        traverse(root->left);
        traverse(root->right);
        //将容器中的值赋值给结果容器
        if(root->left==root->right)
        {
            string s;
            
            for(int i=0;i<temp.size();i++)
            {
                s+=temp[i];
                if(i!=temp.size()-1)
                    s+="->";
            }
            
            ans.push_back(s);
        }
        //返回上一个结点前弹出当前结点
        temp.pop_back();
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        traverse(root);
        return ans;
    }