补题Codeforces Round 905 (Div. 2) （A~F C是真不会啊）（set真好用）

今天补题了么

已于 2023-11-10 19:57:46 修改

阅读量239

点赞数

分类专栏： Codeforces 文章标签：算法

于 2023-11-10 19:51:22 首次发布

本文链接：https://blog.csdn.net/weixin_61825750/article/details/134337314

版权

Codeforces 专栏收录该内容

55 篇文章 6 订阅

订阅专栏

这场套路题比较多，思维量少，主要都是离散化处理 + 二分。

1888A - Chemistry

题意：给定一个只含有字母的字符串，要求删掉k个字符后，对其各字符重排能形成回文。

思路：若最后剩余奇数个字符，则必然有一个字母的个数为奇数，其余都为偶数，若剩余偶数个字符，必须保证剩余的所有字母个数都为偶数。

// Problem: A. Chemistry
// Contest: Codeforces - Codeforces Round 905 (Div. 2)
// URL: https://codeforces.com/contest/1888/problem/A
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N=1e05+10;
const LL mod=1e09+7;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >t;
priority_queue<LL> q;
LL gcd(LL a, LL b){
	return b > 0 ? gcd(b , a % b) : a;
}

LL lcm(LL a , LL b){
	return a / gcd(a , b) * b;
}
void solve() 
{
	int n , k;
	cin >> n >> k;
	int cnt[26];
	memset(cnt , 0 , sizeof cnt);
	int odd = 0;
	string s;
	cin >> s;
	for(int i = 0 ; i < n ; i ++){
		cnt[s[i] - 'a']++;
	}
	for(int i = 0 ; i < 26 ; i ++){
		if(cnt[i] & 1){
			odd ++;
		}
	}
	if((n - k) & 1){
		k -= (odd - 1);
		if(k < 0){
			cout<<"NO\n";
		}
		else{
			cout<<"YES\n";
		}
	}
	else{
		k -= odd;
		if(k < 0 || k % 2 == 1){
			cout<<"NO\n";
		}
		else{
			cout<<"YES\n";
		}
	}
	
}            
int main() 
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cout.precision(10);
    int t=1;
	cin>>t;
    while(t--)
    {
    	solve();
    }
    return 0;
}

1888B - Raspberries

题意：给定一个数组，每次操作能够将数组其中一个数加一，要求能够使数组逐个相乘后能被k整除的最小操作数。

思路：观察到k = 2、3、4、5，当k为素数时，只需要考虑将数组中其中一位加到k的倍数即可。当k = 4 即非素数时，有两种操作方法：1、将其中一个数变为4的倍数。2、将两个数变为2的倍数。分别求最小操作数即可。

// Problem: B. Raspberries
// Contest: Codeforces - Codeforces Round 905 (Div. 2)
// URL: https://codeforces.com/contest/1888/problem/B
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N=1e05+10;
const LL mod=1e09+7;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >t;
priority_queue<LL> q;
LL gcd(LL a, LL b){
	return b > 0 ? gcd(b , a % b) : a;
}

LL lcm(LL a , LL b){
	return a / gcd(a , b) * b;
}
void solve() 
{
	int n , k;
	cin >> n >> k;
	if(k != 4){
		int out = 100;
		for(int i = 0 ; i < n ; i ++){
			int x;
			cin>>x;
			out = min(out , x % k ? k - x % k : 0);
		}
		cout<<out<<endl;
	}	
	else{
		int out1 = 100, out2 = 0;
		for(int i = 0 ; i < n ; i ++){
			int x;
			cin >> x;
			out1 = min(out1 , x % k ? k - x % k : 0);
			if(out2 < 2 && !(x & 1)){
				out2 ++;
			}
		}
		cout << min(out1 , 2 - out2)<<endl;
	}
}            
int main() 
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cout.precision(10);
    int t=1;
	cin>>t;
    while(t--)
    {
    	solve();
    }
    return 0;
}

1888D2 - Dances (Hard Version) 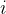$i$

题意：给定长度为 n - 1 的数组 a 和长度为 n 的数组 b 。定义 $c[i]$ 为数字 i 与数组a合并之后构成的长度为n的数组。接下来能够进行若干次操作：将c 、 b数组同时删去一个数。定义 $[c[i] , b]$ 为将b、c数组重新排序后能够使得 $\forall i(c[i] < b[i])$ 的最小操作数。求解 $\sum _{i = 1} ^{n}([c[i] , b])$ 。

思路：显然需要对b、c数组进行从小到大排序，要使得操作数尽可能的少，需要删掉b数组的前k个数跟c数组的后k个数。于是我们需要记录一个辅助数组 $d$ , 令 $d[i] = min_{j} (b[j] > c[i])$ 。换句话说也就是要让 $c[i] < b[i]$ 至少需要删掉 $d[i] - i$ 个数，需要的最少操作数为 $max_{i = 1}^{n}(d[i] - i)$ 。在 $[c[i] , b]$ i 逐渐变大的过程之中，起先 i 这个数是在数组的第一位的。之后慢慢会与后面相邻数互换位置。例如：当 $i$ 在数组第 $j$ 位时，当 $i > c[j + 1]$ 时，实现互换，其中 $d[j] = d[j + 1]$ , $d[j + 1]$ 需要重新找，而找这个 $d[j + 1]$ 的过程也是逐步递增的，因此只需要双指针 $l , r$ 来表示数字 $i$ 在当前数组第 $l$ 位，以及 $min_{r}(d[r] > i )$ 。每次交换由于只有 $d[j] , d[j + 1]$ 会改变，因此只需要比较这两个和当前最小操作数即可。由于 $i$ 的取值可能很大，而数组的大小不多，因此需要离散化处理，i 在递增的过程中并不总是会改变操作数，能改变操作数的条件为 $i \geq b[r]$ 或者 $i > c[l]$ ，如此便能实现离散化。

// Problem: D1. Dances (Easy version)
// Contest: Codeforces - Codeforces Round 905 (Div. 2)
// URL: https://codeforces.com/contest/1888/problem/D1
// Memory Limit: 256 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N=1e05+10;
const LL mod=1e09+7;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >t;
priority_queue<LL> q;
LL gcd(LL a, LL b){
	return b > 0 ? gcd(b , a % b) : a;
}

LL lcm(LL a , LL b){
	return a / gcd(a , b) * b;
}
void solve() 
{
	LL n , m;
	cin >> n >> m;
	LL c[n + 5];
	LL b[n + 5];
	LL a[n + 5];
	LL out = 0;
	a[0] = 1;
	b[n] = 1e18;
	a[n] = m;
	for(int i = 1 ; i < n; i ++)
		cin>>a[i];
	sort(a , a + n);
	for(int i = 0 ; i < n ; i ++)
		cin>>b[i];
	sort(b , b + n);
	LL ans = 0;
	LL l = 0;
	for(int i = 0 ; i < n ; i ++){
		while(a[i] >= b[l]) l ++;
		c[i] = l;	
	}
	l = 1;
	LL id = 0 ,r = 0;
	for(int i = 0 ; i < n ;i ++){
		ans = max(c[i] - i , ans);
	}
	for(int i = 1 ; i <= m ;){
		while(l < n && i > a[l]){
			c[l - 1] = c[l];
			ans = max(c[l - 1] - (l - 1) , ans);
			l ++;		
		}
		a[l - 1] = i;
		while(r < n && i >= b[r]) r ++;
		c[l - 1] = r;
		ans = max(c[l - 1] - (l - 1) , ans);
		LL next = min(m + 1 , min(a[l] + 1 , b[r]));
		out += (next - i) * ans;
		i = next;
	}
	cout<<out<<endl;
}            
int main() 
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cout.precision(10);
    int t=1;
	cin>>t;
    while(t--)
    {
    	solve();
    }
    return 0;
}

1888E - Time Travel

题意：一个无向图，共有n个点和m条边，且共有 t 个时间段限制，每条边只会在相应的时间段有效。下面共有按顺序的 k 个时间段。对于每个时间段你可以选择不走或者走一条边。试问能否从第一个时间段开始从1号节点走到n号节点。

思路：本题同今年CSP-J 2023 旅游巴士差不多，在堆优化的dijkstra算法上将距离改为时间段即可。对于每个点而言，到达的时间越早越好（因为后继就有更多的时间段可供选择）。因此用set存储每个时间段的次序大小。假设当前时间为 $t_{1}$ , 从 $a$ 走到 $b$ 为 $a$ 到 $b$ 这条边所处时间段的大于 $t_{1}$ 的次序。用最短路求出到达各点的最短时间即可。

// Problem: E. Time Travel
// Contest: Codeforces - Codeforces Round 905 (Div. 2)
// URL: https://codeforces.com/contest/1888/problem/E
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N=2e05+10;
const LL INF=1e09+7;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >t;
priority_queue<LL> q;
LL gcd(LL a, LL b){
	return b > 0 ? gcd(b , a % b) : a;
}

LL lcm(LL a , LL b){
	return a / gcd(a , b) * b;
}
struct node{
	int num;
	int dis;
	bool operator > (const node &t) const
	{
		return dis > t.dis;
	}
}tmp;
int dis[N];
int isv[N];
int n , k , s;
vector<node>tr[N];
set<int>st[N];
void dij(int s)
{
	for(int i = 0 ; i < N ; i ++){
		dis[i] = INF;
	}
	priority_queue<node,vector<node> , greater<node> > q;
	q.push({s,0});
	dis[s] = 0;
	while(!q.empty())
	{
		tmp = q.top();
		int x = tmp.num;
		int t = tmp.dis;//时间
		q.pop();
		if(isv[x] == 1)
			continue;
		isv[x] = 1;
		int len = tr[x].size();
		for(int i = 0 ; i < len ; i ++ )
		{
			node now = tr[x][i];
			int tt = now.dis;//目标时间
			auto it = st[tt].upper_bound(t);
			int len = *it;
			int e = tr[x][i].num;
			if(dis[e] > len)
			{
				dis[e] = len;
				q.push({e,dis[e]});
			}
		}
	}
}

void solve() 
{
	cin >> n >>k;
    s = 1;
	int x;
	for(int i = 1 ; i <= k ; i++){
		cin>>x;
		while(x --){
			int a , b;
			cin >> a >> b;
			tr[a].pb({b , i});
			tr[b].pb({a , i});
		}
	}
	cin>>x;
	for(int i = 1 ; i <= x; i ++){
		int time;
		cin>>time;
		st[time].insert(i);
	}
	for(int i = 0 ; i <= k ; i ++){
		st[i].insert(INF);
	}
	dij(1);
	if(dis[n] != INF){
		cout<<dis[n];
	}
	else{
		cout<<-1;
	}
}            
int main() 
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cout.precision(10);
    int t=1;
//	cin>>t;
    while(t--)
    {
    	solve();
    }
    return 0;
}

1888F - Minimum Array

题意：给定一个数组a，下面给了q行，每行包含了 $l , r , x$ ,代表了 a 中 $[l , r]$ 上所有元素加上 $x$ 。

求整个过程中出现的按照次序最小的数组。

思路：区间加自然想到了用差分数组来表示，构造辅助数组b， $b[i] = a[i] - a[i - 1]$ ，对于每一轮操作，只需要令 $b[l] =b[l] + x , b[r + 1] =b[r + 1] -x$ 。而对于最小的数组而言，只需要让b中第一个非零元素小于0即可。而想要动态的维护最小的非0元素下标，只需要用set即可。若碰到了更小的数组，更新一下此时的询问组数索引，然后将b数组清空，在清空的过程只需要将set中有的值清空即可，然后再清空set。最终通过最小数组的询问组数索引来求出最小数组即可。

// Problem: C. Minimum Array
// Contest: Codeforces - Codeforces Round 905 (Div. 1)
// URL: https://codeforces.com/contest/1887/problem/C
// Memory Limit: 256 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N=1e05+10;
const LL mod=1e09+7;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >t;
priority_queue<LL> q;
LL gcd(LL a, LL b){
	return b > 0 ? gcd(b , a % b) : a;
}

LL lcm(LL a , LL b){
	return a / gcd(a , b) * b;
}
struct Node{
	LL l , r , num;	
};
void solve() 
{
	int n;
	cin>>n;
	LL a[n + 5] = {0};
	int min_idx = -1;
	for(int i = 1 ; i <= n ; i ++)
		cin>>a[i];
	LL dif[n + 5];
	memset(dif , 0 , sizeof dif);
	set<int>st;
	int op;
	cin>>op;
	Node o[op];
	for(int i = 0 ; i < op ; i ++){
		cin>>o[i].l>>o[i].r>>o[i].num;
		dif[o[i].l] += o[i].num;
		dif[o[i].r + 1] -= o[i].num;
		if(dif[o[i].l] != 0)
			st.insert(o[i].l);
		else
			st.erase(o[i].l);
		if(dif[o[i].r + 1] != 0)
			st.insert(o[i].r + 1);
		else
			st.erase(o[i].r + 1);
		auto it = st.begin();
		int ans = *it;
		if(ans != 0){
			if(dif[ans] < 0){
				min_idx = i;
				for(auto it : st){
					dif[it] = 0;
				}
				st.clear();
			}
		}
	}
	memset(dif  , 0 , sizeof dif);
	for(int i = 0 ; i <= min_idx ; i ++){
		dif[o[i].l] += o[i].num;
		dif[o[i].r + 1] -= o[i].num;
	}
	LL chan = 0;
	for(int i = 1 ; i <= n ; i ++){
		chan += dif[i];
		a[i] += chan;
	}
	for(int i = 1 ; i <= n ; i ++){
		cout<<a[i]<<" ";
	}
	cout<<endl;
}            
int main() 
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cout.precision(10);
    int t=1;
	cin>>t;
    while(t--)
    {
    	solve();
    }
    return 0;
}