学懂最小生成树（克鲁斯卡尔算法）

本节，小编将带大家了解最小生成树的第二种构成算法——克鲁斯卡尔算法（Kruskal algorithm） 

当然，对另一种算法感兴趣的朋友可以看看之前的这篇文章:学懂最小生成树（普里姆算法）

目录

一.实现原理

 二.代码实现

---

一.实现原理

克鲁斯卡尔算法的思想是：

将所有边从小到大排序，然后依照边从小到大将顶点链式连接起来，直到所有的顶点连成一条链。

原理图：

CSDN@就要宅在家

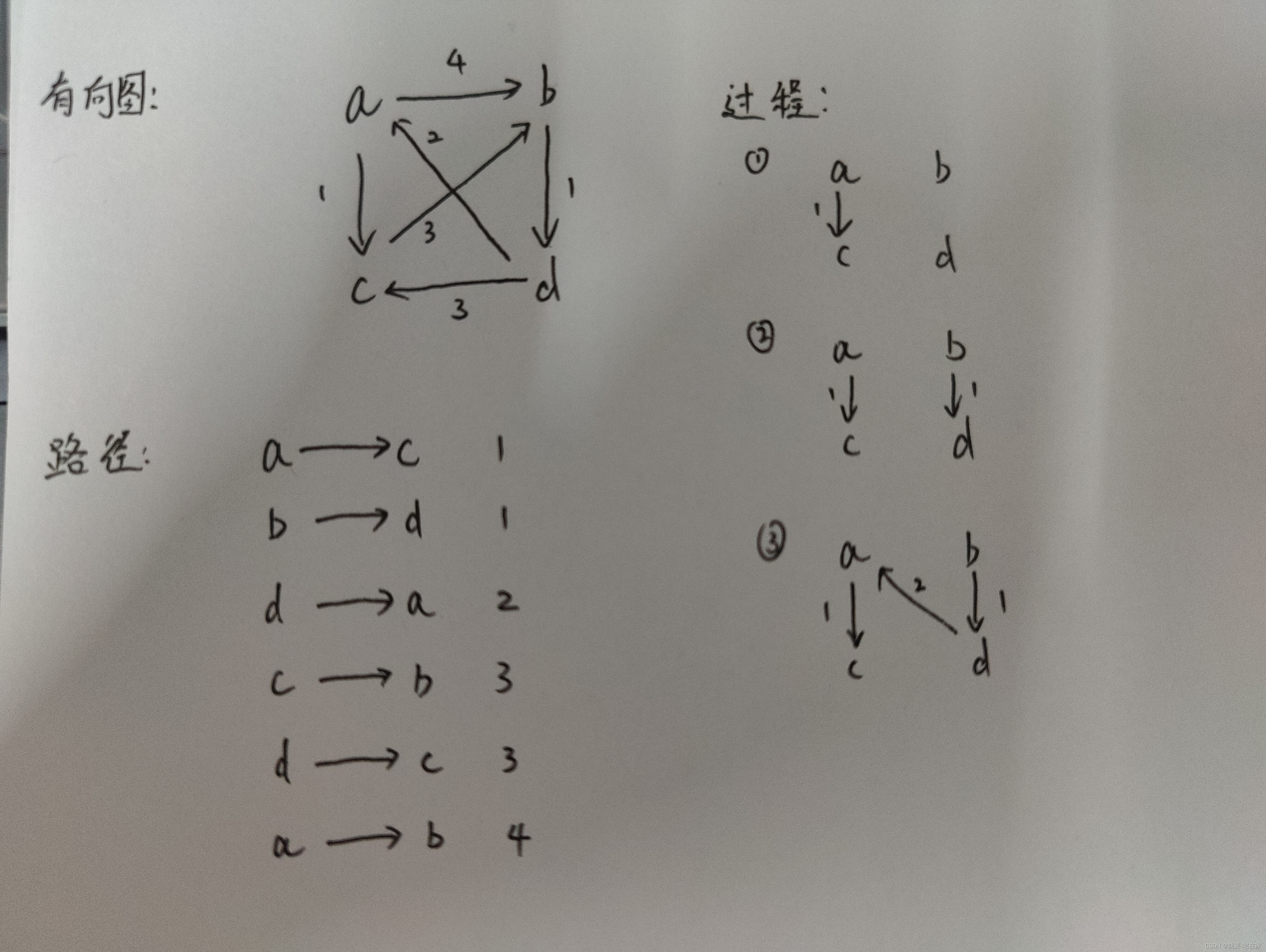
 二.代码实现

实现克鲁斯卡尔算法，我们需要准备两个“工具”，一是结构体数组，里头存放边和该边的两个顶点，用途是升序存放边；二是下标数组，用途是存放到到每个顶点的最小边的顶点下标。

以上图为例：

下标数组设为int vexlist[4];

最终里头存放的下标分别

vexlist[0]	vexlist[1]	vexlist[2]	vexlist[3]
0	3	0	1

以vexlis[1]为例，意思就是到顶点b的最小边是d指向的。

上代码！

void MiniTree_kruskal(UND* u)//排序邻接矩阵所有边权值，从小到大放入克鲁斯卡尔数组
{
	MiniTree_K tm;
	int vexlist[MAXVEX];//建立顶点数组，用于标识个个顶点分量
	sort_K(*u, tm);//升序排序边
	for (int i = 0; i < u->vexnum; i++)//初始化下标数组
	{
		vexlist[i] = i;
	}
	for (int i = 0; i < u->arcnum; i++)//主循环
	{
		int v1 = Findvex(u, tm[i].head);//找这个边的头下标
		int v2 = Findvex(u, tm[i].tail);//找尾下标
		if (vexlist[v1] != vexlist[v2])
		{
			cout << tm[i].head << "->" << tm[i].tail << endl;//打印
			int k = vexlist[v2];//如果有的顶点已经与尾连接起来，将它的vexlist指向头，防止出现路径循环
			for (int j = 0; j < u->vexnum; j++)//找顶点是否与尾连起来
			{
				if (vexlist[j] == k)//如果与尾连起来,那该顶点与尾一起指向头
					vexlist[j] = vexlist[v1];
			}
		}
	}

}
void sort_K(UND u, MiniTree *tm)//排序
{
	int sub = 0;//
	for (int n = 0; n < u.arcnum; n++)//
	{
		int x = 0, y = 0, mininum = Maxnum;
		for (int i = 0; i < u.vexnum; i++)//
		{
			for (int j = 0; j < u.vexnum; j++)
			{
				if (u.form[i][j] < mininum)
				{
					x = i; 
					y = j;
					mininum = u.form[i][j];
				}
			}
		}
		tm[sub].head = u.list[x];
		tm[sub].tail = u.list[y];
		tm[sub].weight = u.form[x][y];
		u.form[x][y] = Maxnum;
		sub++;
	}
}

---

😗创作不易，恳请三连支持，如有错误，敬请斧正