动态规划（dp）-最优路径

蒜头君要回家，已知蒜头君在 左下角(1,1)位置，家在 右上角(n,n)坐标处。蒜头君走上一个格子就会花费相应体力，而且蒜头君只会往家的方向走，也就是只能往上，或者往右走。蒜头君想知道他回到家需要花费的最少体力是多少。
例如下图所示，格子中的数字代表走上该格子花费的体力:

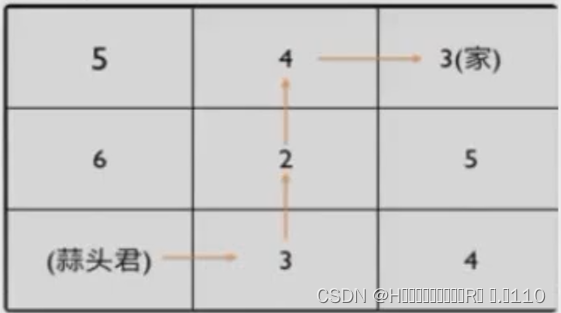
对于该图来说，最优策略已在图上标出，最少花费体力为:3+2+4+3=12。我们把走到一个点看做一个状态，对蒜头君来说，走到一个点只有两种方式，一个是从下面走到该点，一种是从左边走到该点。那么点(i,j)要么是从(i- 1,j)走到(i,j)，要么是从点(i,j - 1)走到(i,j)。所以从哪个点走到(ù,j)就是一个 决策。接下来，我们用 dp(i,j)来代表走到点(i,j)一共花费的最少体力。我们需要花费最少力气走到家，所以可以得到状态转移方程:dp(i,j)= min(dp(i-1,j),dp(i,j-1))+ aij。根据转移方程，我们可以推出走到每个点花费的最少体力。
对于图中的边界点，要在转移前加上判断是否为边界，如:点(1,3)只能从点(1,2)走过来，点(3,1)只能从点(2,1)走过来等等。

动态规划的题目的核心是写出状态转移方程，对于一个动态规划的题目，如果我们能写出转移方程那么代码实现就变得简单多。大部分的动态规划题目，在计算出转移方程后，可以用类似于递推的循环结构，来写出代码。

注：输入样例将上图倒回来用数组存储，所以条件改为只能向下走和向左走

输入样例：

3
0 3 4
6 2 5
5 4 3

输出样例：
12

import java.util.*;

public class LANQIAO1 {
    public static int[][] a = new int[110][110];
    public static int[][] dp = new int[110][110];
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                a[i][j] = sc.nextInt();
            }
        }
        // 从1 1开始，以1 1为起点
        dp[1][1] = 0;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                // 将起点情况排除
                if(i == 1 && j == 1){
                    continue;
                }
                // 处理两种边界情况
                else if(i == 1){
                    dp[i][j] = dp[i][j - 1] + a[i][j];
                }
                else if(j == 1){
                    dp[i][j] = dp[i - 1][j] + a[i][j];
                }
                // 取二者较小值
                else {
                    dp[i][j] = Math.min(dp[i][j-1] , dp[i-1][j]) + a[i][j];
                }
            }
        }
        System.out.println(dp[n][n]);
        return;
    }
}