蓝桥杯竞赛向(C/C++语言)之字符串算法篇

最新推荐文章于 2025-05-21 12:04:25 发布
最新推荐文章于 2025-05-21 12:04:25 发布
阅读量911 收藏 13
点赞数 25
分类专栏： 蓝桥杯篇 文章标签： 算法 蓝桥杯 c语言
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_62188419/article/details/146467602
版权

前言

本次博客先会输出DFS的一些题目，DFS蓝桥考的真的不少，掌握需要大量的刷题，这点题目是完全不够的，有时间的话可以去网站刷，之后是字符串的内容

黄金树

黄金树
DFS 和 树结合也是常考题目，每年基本上会有关于树问题的题目
这个题确实不难，对DFS熟悉的可以轻松码出来

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define inf 0x3f3f3f3f
#define endl '\n'
#define int long long 
#define ld long double
#define vt vector<int> 
const int mod = 1e9 + 7;
const int N = 1e5 + 7;
int n;
struct node{
  int val,left,right;//儿子
}w[N];
int ans;
void dfs(int x,int go)
{
    if(x > n) return;
    if(go == 0) ans += w[x].val;
    int ls = w[x].left;
    int rs = w[x].right;
    if(ls != -1) dfs(ls,go + 1);
    if(rs != -1) dfs(rs,go - 1);
    if(ls == -1 && rs == -1) return;
}
void solve()
{
  cin >> n;
  for(int i = 1;i <= n;i++) cin >> w[i].val;
 for(int i = 1;i <= n;i++) cin >> w[i].left >> w[i].right;
 dfs(1,0);
 cout << ans;
}
signed main()
{
 ios::sync_with_stdio(false);
 cin.tie(0),cout.tie(0);
 int _ = 1; 
 //cin >> _;
 while(_ --) solve();
    return 0;
}

混境之地5
还是跑图题，注意要加记忆化搜索，否则会T
dp数组的意义就是dp[i][j][k]表示用了k次（0/1）次是否能到i，j这个位置

#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 1;
int mp[N][N];
int n,m,k;
int x1,x2,fy,y2; 
int dx[] = {0,0,1,-1};
int dy[] = {1,-1,0,0};
int dp[N][N][2];
bool h(int x,int y)
{
  return x >= 1 && x <= n && y >= 1 && y <= m;
}
bool dfs(int x,int y,int t)
{
  if(x == x2 && y == y2) return true;
  if(dp[x][y][t] != -1) return dp[x][y][t];
  for(int i = 0; i <= 3;i ++)
  {
    int nx = x + dx[i],ny = y + dy[i];
    if(!h(nx,ny)) continue;
    if(!t)
    {
      //用
    if(mp[x][y] + k >= mp[nx][ny] && dfs(nx,ny,1)) return dp[x][y][t] = true; 
    //不用
    if(mp[x][y] >= mp[nx][ny] && dfs(nx,ny,0))  return dp[x][y][t] = true;
    }
    else
    {
       if(mp[x][y] >= mp[nx][ny] && dfs(nx,ny,1)) return dp[x][y][t] = true; 
    }
  }
  return dp[x][y][t] = false;
}
int main()
{
  memset(dp,-1,sizeof(dp));
  ios::sync_with_stdio(false);
  cin.tie(0),cout.tie(0);
   cin >> n >> m >> k;
 cin >> x1 >> fy >> x2 >> y2;

  for(int i = 1; i <= n ; i++)
  {
    for(int j = 1; j <= m; j++) cin >> mp[i][j];
  }
  cout << (dfs(x1,fy,0) ? "Yes" :" No")<< '\n';
    
  
  return 0;
}

混境之地2
这个题和上面那个很像，但是有区别，这个题行走只要不走到墙可以无限转圈，所以要加个vis数组，记得要回溯，不然包错的

#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 1;
char mp[N][N];
int n,m,k;
int x1,x2,yf,y2; 
int dx[] = {0,0,1,-1};
int dy[] = {1,-1,0,0};
int dp[N][N][2];
int vis[N][N];
bool h(int x,int y)
{
  return x >= 1 && x <= n && y >= 1 && y <= m;
}
bool dfs(int x,int y,int t)
{
  if(x == x2 && y == y2) return true;
  if(dp[x][y][t] != -1) return dp[x][y][t];
  for(int i = 0; i <= 3;i ++)
  {
    int nx = x + dx[i],ny = y + dy[i];
    if(vis[nx][ny] == 1) continue;
    vis[nx][ny] = 1;
    if(!h(nx,ny)) continue;
    if(!t)
    {
      //用
    if(mp[nx][ny] == '#'&& dfs(nx,ny,1)) return dp[x][y][t] = true; 
    //不用
    if(mp[nx][ny] == '.' && dfs(nx,ny,0))  return dp[x][y][t] = true;
    }
    else
    {
      if(mp[nx][ny] == '.' && dfs(nx,ny,1)) return dp[x][y][t] = true; 
    }
    vis[nx][ny] = -1;//要注意回溯
  }
  return dp[x][y][t] = false;
}
int main()
{
  memset(dp,-1,sizeof(dp));
   memset(vis,-1,sizeof(vis));
  ios::sync_with_stdio(false);
  cin.tie(0),cout.tie(0);
   cin >> n >> m;
  cin >> x1 >> yf >> x2 >> y2;
  for(int i = 1; i <= n ; i++)
  {
    for(int j = 1; j <= m; j++) cin >> mp[i][j];
  }
  cout << (dfs(x1,yf,0) ? "Yes" :" No")<< '\n';
  return 0;
}

字符串

本次讲的算法有kmp等(自己看目录),ac自动机会给个链接，还有一些例题。。。要吐了

KMP

KMP是一种字符串匹配算法，看到匹配或者一些玩前后缀的时候可以想这个，核心是处理nex数组（不要起名为next，会和库里的重复。。。。。）比如字符串p 在 s中出现的次数，朴素会到O（n * m）级别，KMP只需O（n + m）级别，不用研究nex数组怎么来的，会用就行
nex[i]表示在i这个位置，最长真相同前后缀的长度，也表示匹配失败时应该滚去的位置
比如 abaacd 的nex 就是0 0 1 1 0 0
模板

//n为字符串长度
注意：char s[100];cin >> s + 1;
  int n = strlen(s + 1);//同步
nex[0] = nex[1] = 0;
for (int i = 2, j = 0; i <= n; i++)
{
    while (j && p[i] != p[j + 1]) j = nex[j];
    if (p[i] == p[j + 1]) j++;
    nex[i] = j;
}

自己匹配自己的模板

#include <bits/stdc++.h>
//标准 KMP算法
//在 s中查找p出现的次数
using namespace std;
const int N = 1e6 + 1;
char s[N], p[N];
int nex[N], ans;
int main()
{
   // cin >> p + 1 >> s + 1;
    int n = strlen(p + 1);
    int m = strlen(s + 1);
    //进行处理nex数组
    nex[0] = nex[1] = 0;
    for (int i = 2, j = 0; i <= n; i++)
    {
        while (j && p[i] != p[j + 1]) j = nex[j];
        if (p[i] == p[j + 1]) j++;
        nex[i] = j;
    }  
    //    //对于样例abcabc  //  nex 为  0 0 0 1 2 3
    for (int i = 1, j = 0; i <= m; i++)
    {
        while (j && s[i] != p[j + 1]) j = nex[j];
        if (s[i] == p[j + 1]) j++;
        if (j == n) ans++;
    }
    cout << ans;
    return 0;
}

例题后面一起放，可能字数会很多（）

Manacher

最开始听别人说的一直以为是马拉车（）原来还真是谐音梗
马拉车算法时有关回文字符串的算法，看到回文可以往这个想
先介绍一个概念为了后面的铺垫，
回文半径：比如字符串aabaa，对于回文中心b，回文半径就是三，但是对于偶数长度的字符串，很尴尬；
所以manacher算法的第一个处理，就是将字符串处理成奇数长度的字符串，把首尾和字符串中间加上特殊字符，比如原来的字符串是abba,处理完之后就变成^#a#b#b#a#@,注意首尾不同，其余都用#处理
对于当前的某一个位置i的回文半径p[i]，说明原来回文串长度是p[i] - 1，很好理解和证明，记住就行。
！重要的是处理
模板，和KMP一样记住就行

 int n = strlen(s + 1);
  //填充  倒着填防止被覆盖，除非额外开一个数组！
  s[0] = '@',s[2 * n + 2] = '$';
  for(int i = 2 * n + 1; i >= 1;i--)
  s[i] = i & 1 ? '#' : s[i >> 1];//写成if判断一个样
   //或者这样
  ns[0] = '@',ns[2 * n + 2] = '$';
  for(int i = 1;i <= 2 * n + 1;i++)
  {
    ns[i] = i & 1 ?'#':s[i >> 1];
  }
  

  //处理
  int c = 0, R = 0; // r是当前最右回文边界，c是中心
  for(int i = 1;i <= 2 * n + 1;i ++)
  {
    int mirror = 2 * c - i;
    p[i] = i < R ? min(R - i, p[mirror]) : 1;
    while(s[i + p[i]] == s[i - p[i]]) p[i]++;
    if(i + p[i] > R) c = i, R = i + p[i];
  }

例题依旧放在后面

字符串哈希

这个感觉是很实用的算法，用数字表示字符串，降低处理字符串的复杂度，比如在s中寻找p的出现次数就可以适用字符串哈希，将每一段的值以O（1）算出
记得开unsigned long long，如果开long long可能会导致哈希冲突，还得设两个标准值，标准值相当于进制，一般是一个质数，比如131等，类比十进制
模板—背下来

//字符串哈希
#include<bits/stdc++.h>
#define ull unsigned long long
const ull base = 131;//base一般是一个质数
const int N = 1e6 + 1;
ull h[N],b[N]; //h[i] 表示s[1-i]的hash ---前缀和
char s[N];
ull getHash(int l,int r)
{
   return h[r] - h[l - 1] * b[r - l + 1];
}
using namespace std;
int main()
{
cin >> s + 1;
int n;
n = strlen(s + 1);
b[0] = 1;
for(int i = 1;i <= n;i++) h[i] = h[i - 1] * base + (int)s[i];//这里直接转成int就行，懒得去减
for(int i = 1;i <= n;i++) b[i] = b[i - 1] * base;//获取base的i次方
//获取子串l - r 的hash
getHash()
  return 0;
}

字典树

给N个字符串S1 到 Sn，查找t是否在这里出现过，朴素的查法就是遍历，比较是否相等，复杂度较高，下面引入更快的方法，字典树，叫做字典树，就是一颗树形结构，每一条边代表一个字符，每一个结点可以存储可以不存储，看具体的题干
模板：
（字典树用的不多，更多的是下面的01trie，主要放在后面重点的讲解）

//下面是利用字典树查找的代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define inf 0x3f3f3f3f
#define endl '\n'
const int N = 1e6 + 1ll;
int nex[N][27]; //nex[i][0]表示从节点i出发，边为a的下一个节点地址
int cnt[N];//cnt[i]表示以节点i为结尾的字符串数量
int idx = 2;//记录结点
void insert(char s[])
{
    int n = strlen(s + 1);
    int x = 1; //从1开始往下走
    //将每一个字符取出操作
for(int i = 1;i <= n;i++)
{
   //不存在这一条边就去开一个边
    if(!nex[x][s[i] - 'a']) nex[x][s[i]-'a'] = idx++;
    //往下走
    x = nex[x][s[i] - 'a'];
}
   cnt[x]++;
}
int check(char s[])
{
    int n = strlen(s + 1);
    int x = 1;
    for(int i = 1;i <= n; i++)
    {
        if(!x) return 0;
        x = nex[x][s[i]-'a'];
    }
    return cnt[x];
}
int main()
{
 ios::sync_with_stdio(false);
 cin.tie(0),cout.tie(0);
    return 0;
}


对nex数组不理解的来看这个图奥，nex[8][‘c’ - ‘a’] = 9;nex[1][‘a’ - ‘a’] = 2;这样基本就能看懂了

01trie树

是一种二叉树 每个叶子节点对应一个二进制数
解决最大异或对问题
01Trie树支持三种操作
插入
查询与x异或的最大的元素
查询比更大的元素的个数，可用于解决逆序对问题
有了字典树的模板，更好写这个了

///字典树
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define inf 0x3f3f3f3f
#define endl '\n'
#define int long long 
const int N = 1e6 + 1; //一般要开已有数据的30倍数
int son[N][2];
int e[N];
int iot = 1;
void insert(int x)
{
    int o = 1;//表示节点编号
    e[o]++;
    for(int i = 30;i >= 0;--i)
    {
        int y = x >> i & 1; //第i位的值
        if(!son[o][y]) son[o][y] = ++iot;
        o = son[o][y];
        e[o]++;
    }
}
//查询Trie中与x异或的最大值
int checkmax(int x)
{
    int res = 0,o = 1;
    for(int i = 30;i >= 0;i --)
    {
        int y = x >> i & 1;
        if(son[o][!y]) o = son[o][!y],res |= (1ll << i);
        else o = son[o][y];
    }
    return res;
}
//查询最小值
int checkmin(int x)
{
    int res = 0,o = 1;
    for(int i = 30;i >= 0;i--)
    {
        int y = x >> i & 1;
        if(son[o][y]) o = son[o][y];
        else o = son[o][!y],res |= 1ll << i; 
    }
    return res;
}
//比x大的数目
int bigcount(int x)
{
    int res = 0,o = 1;
    for(int i = 30;i >= 0;i--)
    {
        int y = x >> i & 1;
        if(y == 0) res += e[son[o][1]];
        if(!son[o][y])break;
        o = son[o][y];
    }
    return res;
}
signed main()
{
 ios::sync_with_stdio(false);
 cin.tie(0),cout.tie(0);
    return 0;
}

关于异或问题，一般会想到前缀和 / 按位运算 / 01trie树/ 线性基
关于线性基，详见OI wiki
这里我介绍的算法都不是详细的，有问题可以去OI wiki的官网，直接搜就能搜的到

例题：算法模板题（题目很简单，就不放链接了）
KMP 和 Hash
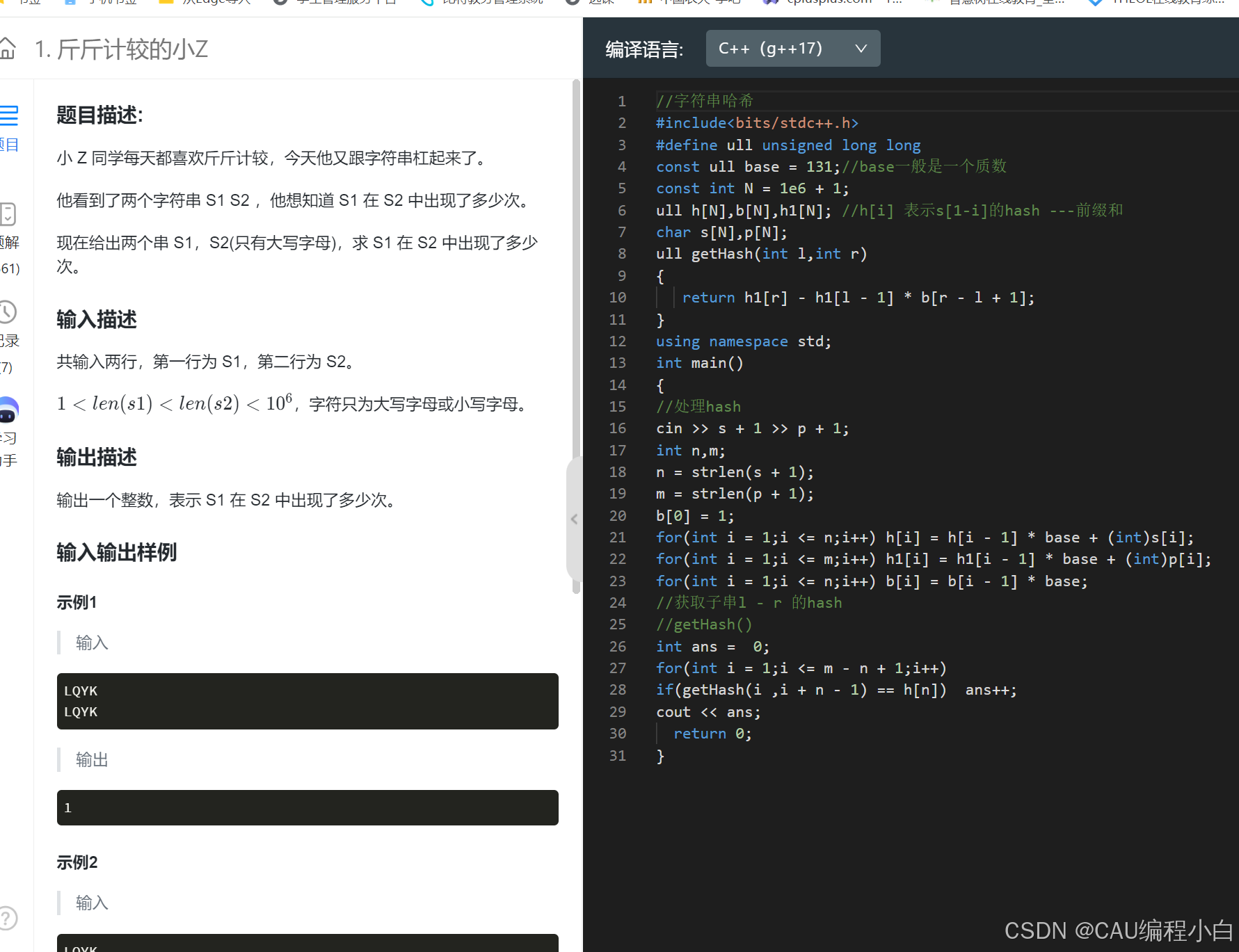
在这里插入图片描述
KMP定义
在这里插入图片描述

manacher
在这里插入图片描述
字典树
在这里插入图片描述
01trie树
在这里插入图片描述
在这里插入图片描述
逆序对的数量这道题也可以使用树状数组来实现，等我讲到那个的吧

下面是一些有难度的题目

最大异或结点

链接
看上去像01，但是发现直接相连的不能这样取异或，所以要加入一个remove函数，每次要把相连的remove掉，但是还要记得复原

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define inf 0x3f3f3f3f
#define endl '\n'
#define int long long 
//思路 01tire写一个remove函数 修改边是不容易的,可以改权值
//将所有信息读入Trie中,对于每一个节点,移除掉与他有关的节点之后,取最大值,最后回溯,再将信息加进来
const int N = 3e6 + 1;
int son[N][2];
vector<int> v[N];//存放信息
int e[N];
int arr[N],fa[N];
int tot = 1;
void insert(int x)
{
   int o = 1;
   e[o]++;
   for(int i = 30;i >= 0; i--)
   {
    int y = x >> i & 1;
    if(!son[o][y]) son[o][y] =  ++tot;
    o = son[o][y];
    e[o]++;
   }
}
void remove(int x)
{
  int o = 1;
   e[o]--;
   for(int i = 30;i >= 0; i--)
   {
    int y = x >> i & 1;
    o = son[o][y];
    e[o]--;
   }
}
int query(int x)
{
  int res = 0;
  int o = 1;
  for(int i = 30;i >= 0; i--)
  {
    int y = x >> i & 1;
    if(son[o][!y] && e[son[o][!y]]) 
    {
        o = son[o][!y];
        res |= (1ll << i);
    }
   else o = son[o][y];
  }
  return res;
}
signed main()
{
 ios::sync_with_stdio(false);
 cin.tie(0),cout.tie(0);
 int n; cin >> n;
 for(int i = 0;i < n;i ++) cin >> arr[i];
 for(int i = 0;i < n;i++)
 {
    cin >> fa[i];
    if(fa[i] != -1)
    v[fa[i]].push_back(i - 1); //从0开始 v[0] 含有 1 3 
    // v[1] 含有2 4 
 }
 for(int i = 0;i < n;i++) insert(arr[i]);
  int ans = 0;
 for(int i = 0;i < n;i++)
 {
    //移除  //arr[i]是当前的节点 移除掉所有与arr[i]相连的节点 v[i]中存放好了个数
    //i - 1是当前节点  e + 1读入是 1 到 n  节点是0 到 n - 1;
   for(auto e : v[i]) remove(arr[e]);
    //计算
   ans = max(ans,query(arr[i]));
    //回溯
   for(auto e : v[i]) insert(arr[e]);
 }
 cout << ans;
    return 0;
}

串的前缀

串的前缀
利用并查集 + KMP

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 +10;
#define int long long
char s[N];
int n,ans;
int ne[N];
int find(int x)
{
    if(!ne[x]) return x;
    return ne[x] = find(ne[x]);
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    cin >> n >> s + 1;
   for(int i = 2,j = 0;i <= n;i++)
   {
     while(j && s[i] != s[j + 1]) j = ne[j];
     if(s[i] == s[j + 1]) j++;
     ne[i] = j;
   }
   //i   1 2 3 4 5 6 7 8
   //fin 1 2 1 2 1 2 1 2 
   //ans 0 0 2 2 4 4 6 6
   //nex 0 0 1 2 3 4 5 6 
    for(int i = 2;i <= n;i++)
    {
      if(ne[i]) ans += i - find(i);
    }
    cout << ans << endl;
    return 0;
}

你也喜欢幸运字符串吗

链接
dp数组的意义是dp[i]表示以0到i为前缀的个数
dp[nex[i]] = dp[nex[i]] + dp[i] //想一想就明白了，注意要倒着处理，因为nex数组
比如abcabc
dp[nex[6] = 3] += dp[6];

代码


```cpp
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define inf 0x3f3f3f3f
#define endl '\n'
#define int long long 
const int N = 1e6 + 1;
char s[N];
int nex[N];
int dp[N];
signed main()
{
 ios::sync_with_stdio(false);
 cin.tie(0),cout.tie(0);
 int n; cin >> n;
cin >> s + 1;
for(int i = 2,j = 0;i <= n;i ++)
{
    while(j && s[i] != s[j + 1]) j = nex[j];
    if(s[i] == s[j + 1]) j++;
    nex[i] = j;
}
for(int i = 1;i <= n;i++) dp[i] = 1;
for(int i = n;i >= 1;i--) dp[nex[i]] += dp[i]; //加入前缀
int ans = 0;
for(int i = 1;i <= n;i++) ans += dp[i];
cout << ans;
    return 0;
}

异或和之差

链接
这个还是蛮恶心的
知道思路也写起来很费劲
就是对于每一个分割位置i，求出前面异或的最大 - 后面的最小 || 后面最大减去前面最小 记录四个数组开写。。。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define inf 0x3f3f3f3f
#define endl '\n'
#define int long long 
const int N = 1e6 + 1;
int sonl[N][2],sonr[N][2];
int premax[N],premin[N];
int sufmax[N],sufmin[N],arr[N];
int prexor[N],sufxor[N];
int totl = 2;
void insert(int son[][2],int x)
{
    int o = 1;
    for(int i = 20;i >= 0;i --)
    {
        int y = x >> i & 1;
        if(!son[o][y])
        {
            son[o][y] = totl++;
        }
        o = son[o][y];
    }
}
int checkmax(int son[][2],int x)
{
   int res = 0, o = 1;
   for(int i = 20;i >=0; i --)
   {
    int y = x >> i & 1;
    if(son[o][!y])
    {
        o = son[o][!y];
        res |= 1ll << i;
    }
    else o = son[o][y];
   }
   return res;
}
int checkmin(int son[][2],int x)
{
    int res = 0, o = 1;
    for(int i = 20;i >= 0;i --)
    {
        int y = x >> i & 1;
        if(son[o][y]) o = son[o][y];
        else
        {
            o = son[o][!y];
            res |= 1ll << i;
        }
    }
  return res;
}
signed main()
{
 ios::sync_with_stdio(false);
 cin.tie(0),cout.tie(0);
 int n; cin >> n;
 for(int i = 1;i <= n;i++) cin >> arr[i];
 insert(sonl,0);
 insert(sonr,0);

 for(int i = 0;i <= n + 1;i++)
 {
    premin[i] = sufmin[i] = inf;
 }
 for(int i = 1;i <= n;i++)
 {
    prexor[i] = prexor[i - 1] ^ arr[i];
    premax[i] = max(premax[i - 1],checkmax(sonl,prexor[i]));
    premin[i] = min(premin[i - 1],checkmin(sonl,prexor[i]));
    insert(sonl,prexor[i]);
 }
 for(int i = n;i >= 1;i --)
 {
    sufxor[i] = sufxor[i + 1] ^ arr[i];
    sufmax[i] = max(sufmax[i - 1],checkmax(sonr,sufxor[i]));
    sufmin[i] = min(sufmin[i - 1],checkmin(sonr,sufxor[i]));
    insert(sonr,sufxor[i]);
 }
 int ans = 0;
 for(int i = 1;i < n;i ++)
 {
    ans = max(ans,max(sufmax[i + 1] - premin[i],premax[i] - sufmin[i + 1]));
 }
 cout << ans;
    return 0;
}

到这吧，下次更新十三届A组真题 / 数论
求三连！！！！！

(蓝桥杯C/C++）——基础算法(上）
2402_82385099的博客
11-05 5437
二分法是一种高效的查找方法，它通过将问题的搜索范围一分为二(两边具有明显的区别)，迭代地缩小搜索范围，直到找到目标或确定目标不存在。分法适用于有序数据集合，并且每次迭代可以将搜索范围缩小一半。分法本质上也是枚举，但和暴力枚举不同，二分法利用数据结构的单调性减少了很多不必要的枚举，从而极大地提高了效率，一般可以将O(n)的枚举优化到O(logn)。常见的二分类型有:(1)整数二分(2)浮点二分(3)二分答案(最常见)1.研究并发现数据结构(或答案变量)的单调性。
蓝桥杯c++-蓝桥杯竞赛练习之算法提高题字符串比较.zip
04-14
在准备参加蓝桥杯竞赛的过程中，C++编程语言和算法是关键领域，特别是字符串操作，因为它们经常出现在各种算法题目中。本压缩包文件“蓝桥杯c++_蓝桥杯竞赛练习之算法提高题字符串比较”显然是为帮助参赛者提升这...
蓝桥杯竞赛向（C/C++语言）之简单算法篇
weixin_62188419的博客
03-13 1183
竟然又水了一集下一期开DFS，剪枝，和回溯 和 字符串算法（不要和博主提一些高级算法 听不懂。。。。。
蓝桥杯竞赛向（C/C++语言）
weixin_62188419的博客
03-12 1469
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档。
蓝桥杯C/C++实用知识总结
m0_61443432的博客
04-05 2万+
在Excel表格的B列填分母，每行是前一行的两倍，在B2单元格填写“=B1*2”，然后将鼠标指针移动到B2单元格的右下角，当指针变成十字形状时，按住鼠标左键向下拖拽到第20行，就填好了分母。返回值：如果没有下一个排列组合，则返回false，否则返回true，每执行一次，新的排列放回到原来的空间（例如原来的字符串s会变成新的字符排列顺序）中。两个矩阵A和B相乘，要求A的列数等于B的行数，设A是m×n的矩阵，B是n×u的矩阵，那么乘积C=AB是m×u的矩阵，三重循环，复杂度为O(mnu)。
蓝桥杯竞赛向（C/C++语言）之最后一期真题更新
weixin_62188419的博客
04-18 885
难绷，本来以为上一期就是最后一期关于蓝桥了，没想到北京地区因为大风拖了两个周，。。。还得折磨我两个周，好想学Linux。。。我就做了一下今年的题目，没想到A组题比B组整体简单，更新一下A组的吧先说一下我的四个小时的答题情况和我感觉的难度1.寻找质数 —开幕雷击，好水的题目，甚至你写个n^2的都能过 简单2.黑白棋 把规则用好，我没跑代码，直接推的，如果不是纯推写代码就废一点劲 建议推导 简单3.抽奖 一个简单的模拟 送分 简单。
蓝桥杯竞赛向(C/C++语言)之博主掌握不太好的算法篇(DFS)
weixin_62188419的博客
03-23 1336
下次一定（也有可能去更新14届蓝桥杯A组真题）//会带一点AC自动机 但是不会讲 因为我不会 蓝桥几乎不会考（看水的字数博主沉淀了几天（回来更新了，估计可能只能讲个搜索了，字符串东西很多，下次讲，主要讲搜索的原因是什么捏，（博主刷了一会题，发现搜索做的真的很不好…需要多刷一点题，本次讲解主要以刷题为主，搜索只有多做才能会。。。
蓝桥杯C/C++程序设计 往届真题汇总（进阶篇）
热门推荐
Bit_Dong的博客
03-05 5万+
1. 最短路2. 数字三角形3. 递增序列4. 杨辉三角形5. 跳跃6. 路径7. 迷宫8. 装饰珠9. 明码10. 字串分值11. 作物杂交12. 承压计算13. 全球变暖14. 直线15. 平面切分
【C++】蓝桥杯必备 算法竞赛常用STL万字总结
CPT1024
03-15 4万+
C++ STL标准库 常用函数总结 算法竞赛必备
蓝桥杯手把手教你备战（C/C++ B组）（最全面！最贴心！适合小白！）
lhllhllhl_的博客
01-15 3万+
目前算法竞赛常用的赛制是ACM赛制、OI赛制、IOI赛制，那么这些赛制分别代表什么意思呢？这块我参考了这篇博文，ACM、OI、IOI编程竞赛模式介绍，想了解更多信息的可以跳转查看。
算法竞赛蓝桥杯基因配对问题解析：C++实现字符串匹配与处理方法探讨
05-08
内容概要：本文介绍了蓝桥杯竞赛中基因配对问题的解题思路与代码实现。文章详细描述了如何通过遍历字符串进行基因配对，具体步骤是从字符串的第一位开始，逐步递增遍历到字符串长度的一半为止。为了简化判断过程，...
蓝桥杯c++-蓝桥杯竞赛练习之基础练习题字符串对比.zip
04-15
在准备参加蓝桥杯竞赛的过程中，C++编程语言是重要的工具之一，特别是在基础练习题中，字符串对比是一项基本且至关重要的技能。本文将深入探讨C++中的字符串处理和比较，帮助参赛者提升在这个领域的理解与应用能力。...
2019蓝桥杯B 组C/C++ 题目
03-25
【标题】"2019蓝桥杯B组C/C++题目"涵盖了当年蓝桥杯编程竞赛B组的C++语言试题，这是一个针对C++编程技能的竞技平台，旨在提升参赛者的算法设计与编程能力。蓝桥杯是中国极具影响力的编程比赛之一，对于计算机科学和...
sizeof 和strlen的对比
我爱我想但不嫉妒 我哭我笑但不抱怨 我羞我愧但不悲叹 我怒我恨但不自弃
05-17 938
sizeof 和strlen的对比及数组和指针笔试题解析
高被引二区优化算法——肝癌算法（Liver Cancer Algorithm，LCA）深度解析+性能测试
woaipythonmeme的博客
05-19 1053
LCA的核心机制聚焦于肿瘤在寻找最有利生存环境时所表现出的适应性与侵袭性行为，算法通过演化搜索策略再现肝癌细胞在器官中逐步扩张并主导空间的动态机制，其数学建模确保了算法在解空间内的全局探索能力与局部开采能力之间的高效平衡。为确定肿瘤的体积，我们采用一种基于数学模型的计算方法，假设肿瘤呈半椭球形，该形态已在包括肝癌在内的多种癌症中被观察到。在LCA算法的该阶段中，其设计灵感源自真实肿瘤的扩散过程，假设肿瘤可在竞争环境中逐步选择最优路径深入肝脏的不同区域以实现侵占。）时，目标代理元素的肿瘤位置将被考虑。
水平可见直线--上凸包（andrew算法
2301_80422662的博客
05-18 254
【代码】水平可见直线--上凸包（andrew算法。
《算法笔记》11.7小节——动态规划专题-＞背包问题 问题 C: 货币系统
2401_88085478的博客
05-20 240
举例来说, 使用一个货币系统 {1,2,5,10,...}产生 18单位面值的一些可能的方法是:18x1, 9x2, 8x2+2x1, 3x5+2+1,等等其它。传统地，一个货币系统是由1,5,10,20 或 25,50, 和 100的单位面值组成的。母牛想知道有多少种不同的方法来用货币系统中的货币来构造一个确定的数值。写一个程序来计算有多少种方法用给定的货币系统来构造一定数量的面值。母牛们不但创建了他们自己的政府而且选择了建立了自己的货币系统。(1<= N<=10,000)输入包含多组测试数据。
《算法笔记》11.8小节——动态规划专题-＞总结 问题 E: 最大子矩阵
最新发布
2401_88085478的博客
05-21 157
再后面的若干行中，依次（首先从左到右给出第一行的N个整数，再从左到右给出第二行的N个整数……）给出矩阵中的N2个整数，整数之间由空白字符分隔（空格或者空行）已知矩阵的大小定义为矩阵中所有元素的和。给定一个矩阵，你的任务是找到最大的非空(大小至少是1 * 1)子矩阵。输入是一个N * N的矩阵。输入的第一行给出N (0 < N <= 100)测试数据可能有多组，对于每组测试数据，输出最大子矩阵的大小。已知矩阵中整数的范围都在[-127, 127]比如，如下4 * 4的矩阵。这个子矩阵的大小是15。
第十届蓝桥杯省赛C/C++组真题解析
蓝桥杯竞赛是由中国高等教育学会举办的面向全国大学生的计算机类科技竞赛，包含多个组别，比如C/C++、Java等编程语言组，旨在提高学生综合运用所学知识解决实际问题的能力。蓝桥杯在IT行业和高校计算机专业学生中...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值