DS二叉树—二叉树结点的最大距离

目录

题目描述

思路分析

AC代码

---

题目描述

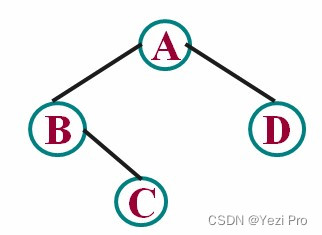
二叉树两个结点的距离是一个结点经过双亲结点，祖先结点等中间结点到达另一个结点经过的分支数。二叉树结点的最大距离是所有结点间距离的最大值。例如，下图所示二叉树结点最大距离是3，C和D的距离。

二叉树用先序遍历顺序创建，#表示空树。计算二叉树结点最大距离和最大距离的两个结点(假设二叉树中取最大距离的两个结点唯一）。

输入

测试次数T

第2行之后的T行，每行为一棵二叉树先序遍历结果（#表示空树）

输出

对每棵二叉树，输出树的结点最大距离和最大距离的结点，输出格式见样例。

输入样例1

3
A##
ABC##EF#G###D##
ABEH###F#K###

输出样例1

0:
5:G D
4:H K

思路分析

这道题对我来说比较难，我足足打了四个小时，因为一开始没有任何的思路，后来我是先找到最大距离，然后想办法找到了两个节点。

找两个节点之间的最大距离，无论这两个节点在哪里，它们一定是属于某一个节点的叶子，也就是说，如果有解，那么解一定会是某个树（子树）的两边。而距离可以用深度来计算，这个满足条件的解的树的左右子树的深度加起来就是最大距离。

也就是说，我们需要找出每棵树的左右子树的深度之和，然后找出最大的就是我们需要的解，这个用一个递归函数可以完成。

然后我们需要去找那两个叶子节点。假设我们已经找到左右子树深度之和最大的节点了，那么需要找的叶子节点就应该是左右子树最深的末端叶子节点。

那么我们需要一个函数能够找出一棵树最深的末端叶子节点，这个用一个递归函数可以解决。

怎么解决的？对于一颗树，它的最深的末端叶子节点应该在深度最大的子树那里，所以我们需要知道子树的深度，再引入一个求深度的函数，这个求树的深度的函数非常NB，是一个学长教的，只用了三行代码搞定。

好了，首先判断左右子树哪一个深度更大（如果其中一颗子树节点为空，那么肯定另一颗不为空的子树深度更大），然后选择深度大的子树继续查找，问题变成了找这颗子树的最深末端节点问题，没错，这就是递归 ，递归结束的条件就是左右子树节点为空。

AC代码

#include <iostream>
#include <string>
#include <queue>
using namespace std;
class BiTreeNode {
public:
    char data,start,end;					//数据域
    int leftdistance=0,rightdistance=0;
    BiTreeNode  *leftChild,  *rightChild;	//左右子树指针
    BiTreeNode():leftChild(NULL), rightChild(NULL){}
    ~BiTreeNode() {}
};

class BiTree {
private:
    BiTreeNode *root;	//根结点指针
    string sTree;		//建树字符串
    int pos;			//标识建树字符串的当前字符位置
    BiTreeNode * CreateTree();//建树私有函数
    int maxdistance=0;
    char start,end;
public:
    BiTree():root(NULL) {};
    void Create(string vArray);	//建树公有接口，参数是特定的先序遍历字符串
    void FindMaxDistance(BiTreeNode*T){
        if(T==NULL)
            return;
        if(T->leftChild==NULL)
            T->leftdistance=0;
        if(T->rightdistance==NULL)
            T->rightdistance=0;
        if(T->leftChild){
            FindMaxDistance(T->leftChild);
            T->leftdistance= max(T->leftChild->leftdistance,T->leftChild->rightdistance)+1;
        }
        if(T->rightChild){
            FindMaxDistance(T->rightChild);
            T->rightdistance= max(T->rightChild->leftdistance,T->rightChild->rightdistance)+1;
        }
        if(maxdistance<T->leftdistance+T->rightdistance){
            if(T->leftChild)
            start= getyezi(T->leftChild);
            else start=T->data;
            if(T->rightChild)
            end= getyezi(T->rightChild);
            else end=T->data;
        }
        maxdistance= max(maxdistance,T->leftdistance+T->rightdistance);
    }
    char getyezi(BiTreeNode*t){
        if(t->leftChild==NULL&&t->rightChild==NULL)
            return t->data;
        if(t->leftChild==NULL)
            return getyezi(t->rightChild);
        if(t->rightChild==NULL)
            return getyezi(t->leftChild);
        if(getheight(t->leftChild)> getheight(t->rightChild))
            return getyezi(t->leftChild);
        return getyezi(t->rightChild);
    }
    int getheight(BiTreeNode*t){
        if(t==NULL)
            return 0;
        return max(getheight(t->leftChild), getheight(t->rightChild))+1;
    }
    void Show(){
        FindMaxDistance(root);
        cout<<maxdistance<<':';
        if(maxdistance)
            cout<<start<<' '<<end;
        cout<<endl;
    }
};
void BiTree::Create(string vArray)
{	pos=0;
    sTree.assign(vArray);	//把参数保存到内部字符串
    root = CreateTree();	//建树成功后root指向根结点
}
BiTreeNode* BiTree::CreateTree() {
    if(pos==sTree.size()||sTree[pos]=='#'){
        pos++;
        return NULL;
    }
    BiTreeNode*T=new BiTreeNode();
    T->data=T->start=T->end=sTree[pos++];
    T->leftChild=CreateTree();
    T->rightChild=CreateTree();
    return T;
}
int main()
{	int t;
    string vArray;
    cin>>t;
    while(t--)
    {	cin>>vArray;
        BiTree myTree;
        myTree.Create(vArray);
        myTree.Show();
    }
    return 0;
}