西工大noj100题
说在前面:所有程序设计题目的题解都是在自己思考过以后看才能有所收获,题解只是一个参考,看懂思路后最好自己从0开始敲一遍!!!
如果对某一题有更好的思路
欢迎评论区交流或者私信我
持续更新~
更新时间:2024.12.29
(目录自动生成在文章右边哦~)
本文优势:
1.以《算法笔记》(胡凡 曾磊)为蓝本,内容充实有依据
2.通俗易懂,初学者也可无障碍阅读
3.精心挑选全站最优博文,为读者提供拓展阅读链接
4.一题多解,拓宽读者题解思路
5.解题过程中带领读者回顾基础知识点
6.对素数等热门题总结出模板,方便读者积累
7.题目完整清晰,题解注释清楚
8.对于较难的题目,给出清晰的解题思路和调试过程
9.题目后用括号标注注意事项或主要解题算法和步骤
10.提供应试技巧和常见错误,助力考生金榜题名
……
考前提醒
1.重视模板:文件这类题是有固定的模板的,不要以为题号比较靠后的题会很难,实际上文件这块儿的难度不会超过循环题。这也提示我们考前一定要准备一些常用的模板,比如排序(可以选择冒泡、快排、归并等等,或者直接用C++算法库里的sort()也可以)字符串的题推荐使用STL。有时遇到解题逻辑没问题,但实际输出和期望不符时可以考虑使用C++的cin,cout,有奇效。
2.先易后难:这也提示我们考试的时候先快速浏览10道题,把一眼看上去就有思路的题先做了,保证拿到通过考试的分数,然后再做算法等较难的题,做题顺序不一定要按照题号顺序来。
3.复制它善:写代码时要养成复制粘贴的好习惯,我说的不是直接复制别人的题解,而是自己写的时候,同一道题目,一些相同结构的循环,函数可以前后复制粘贴;不同的题目,基本的函数库,main函数架构都是一样的吧,也可以复制粘贴,节省时间,考试只有90min,要完成10道题时间还是很不富裕的(进考场还未开考之前听监考老师安排,如果可以先打开cb,就把能include的都包含进去,考的时候cb不强制全屏,可以缩小界面放在考试题目旁边对着敲)
4.细节要看:比如分号,数据类型((比如sqrt(double x),不要降低精度,long long可以有效防止数据溢出,但是int更常用),main和mian,scanf要有&而printf没有&,左右括号不匹配,中英文输入法,以及样例输出中隐含的格式(如空格,换行等)
5.临危不乱:要习惯随时编译并检查输出,或者写完后打断点调试程序,拿到题目可以先分成几个子任务然后分别解决,如上实在解不了的题先选择性跳过,最后有时间再尝试枚举,暴力输出法,或者干脆只解决1-2个子任务,可以通过部分测试样例,拿到一定分数。遇到题目描述不清的要及时举手向监考老师询问。
/*考试能用到的模板基本涵盖在100道noj中,对于部分常用小模板我设置了二级小标题,如判断素数,求整数位数等,读者可以很容易地在目录中找到它们。另外推荐一篇模板总结得还不错的博文:2023西工大NOJ (C语言版) 完结!!!-CSDN博客,读者可自行参考总结*/
/*对与初学者,IDE以及外设的选择推荐看:西北工业大学 NOJ 2023 程序设计基础(C++) 完结撒花(已停止维护)_西工大noj-CSDN博客*/
001:Hello World

#include<stdio.h>
int main(){
printf("Hello World\n");
return 0;
}
注意:Hello和World首字母大写,且中间含空格。在其他题目中也要注意大小写的问题!
另外要注意的是,在使用大部分IDE集成编译环境的时候(如Dev-C++、CodeBlocks等),新建项目的代码文件会给出一份初始代码,里面是包括基础的头文件和main函数的,但在考试和竞赛的时候这些均不会给出,需要同学们自己记忆,当然部分竞赛和考试也允许携带纸质资料,如果万一记不起来了可以翻书查阅。
另外往年同学们犯的错误比较多的情况是:
1.语句结束后忘记写分号
2.函数的()用的是中文输入法
3.main写成mian
4.括号不成对
5.scanf忘记写&符号
6.判断语句只有一个等于号,应该是if(value = = 1)这种形式
7.输入输出不注意大小写,回车,空格等问题
8.不按样例输出的格式来,忘记单位,空格或者单位转换
9.循环条件不注意边界值检验,导致死循环
10.数据类型没用对,或者忘记初始化,或者空间设小了导致溢出
……
总之,以上这些低级错误希望同学们在考试的时候注意检查,有时候编译错误只是因为这些小错。
002:A+B

这里注意要养成良好的变成习惯,每个参数的命名都要有实际意义,比如这里的“和”命名为“sum”,而不要abcdefg这样随意地取参数,这样不仅会降低代码的可读性,有时也会使我们在编写代码的过程中忘记参数的含义,影响思路。
#include <stdio.h>
int main()
{
int a,b,sum;
scanf("%d %d", &a, &b);
sum = a + b;
printf("%d\n", sum);
return 0;
}
003:数据类型大小及范围


注意内存大小是以字节为单位的,比如int对应4字节,所以sizeof(int)= 4,其中sizeof()是反映参数对应数据类型所占的内存大小。
特别地,由于char字符类型只占1字节,所以sizeof()也可以用来求字符数组的大小
这里还需要注意区分sizeof()和 strlen()的区别:

代码示例:
char str[] = "Hello";
printf("strlen: %lu\n", strlen(str)); // 5
printf("sizeof: %lu\n", sizeof(str)); // 6 (因为包含 '\0')
参考题解1:(利用sizeof(),推荐)
#include <stdio.h>
#include <limits.h>
int main() {
int choice;
scanf("%d", &choice);
switch (choice) {
case 1:
printf("%zu,%d,%d\n", sizeof(char), CHAR_MIN, CHAR_MAX);
break;
case 2:
printf("%zu,%d,%u\n", sizeof(unsigned char), 0, UCHAR_MAX);
break;
case 3:
printf("%zu,%d,%d\n", sizeof(short), SHRT_MIN, SHRT_MAX);
break;
case 4:
printf("%zu,%d,%u\n", sizeof(unsigned short), 0, USHRT_MAX);
break;
case 5:
printf("%zu,%d,%d\n", sizeof(int), INT_MIN, INT_MAX);
break;
case 6:
printf("%zu,%u,%u\n", sizeof(unsigned int), 0, UINT_MAX);
break;
case 7:
//printf("%zu,%d,%d\n", sizeof(int), INT_MIN, INT_MAX);
printf("%zu,%ld,%ld\n", sizeof(long), LONG_MIN, LONG_MAX);
break;
case 8:
printf("%zu,%u,%lu\n", sizeof(unsigned long), 0UL, ULONG_MAX);
//printf("%zu,%u,%u\n", sizeof(unsigned int), 0, UINT_MAX);
break;
case 9:
printf("%zu,%lld,%lld\n", sizeof(long long), LLONG_MIN, LLONG_MAX);
break;
case 10:
printf("%zu,%u,%llu\n", sizeof(unsigned long long), 0ULL, ULLONG_MAX);
break;
default:
printf("无效的编号\n");
break;
}
return 0;
}
参考题解2:(暴力枚举,不推荐,但是考试或竞赛中如果实在做不出来可以采用,直接printf()或者完成题目子任务以通过部分测试点,常见赛制都会以通过测试点数量计分)
#include<stdio.h>
int main(){
int a;
scanf("%d",&a);
if(a==1){
printf("1,-128,127");
}
if(a==2)
{
printf("1,0,255");
}
if(a==3)
{
printf("2,-32768,32767");
}
if(a==4)
{
printf("2,0,65535");
}
if(a==5)
{
printf("4,-2147483648,2147483647");
}if(a==6)
{
printf("4,0,4294967295");
}if(a==7)
{
printf("4,-2147483648,2147483647");
}if(a==8)
{
printf("4,0,4294967295");
}
if(a==9)
{
printf("8,-9223372036854775808,9223372036854775807");
}
if(a==10)
{
printf("8,0,18446744073709551615");
}
}
004:平均值

#include <stdio.h>
#include <stdlib.h>
int main()
{
long long a,b,c;
scanf("%lld %lld", &a, &b);
c = (a + b)/2;
printf("%lld\n", c);
return 0;
}
注意:此题虽然题目为整型,但是实际需要long long 长整型才能AC,否则会WA!
另外:要注意各类数据类型的数据范围,比如当数量级超过10^9的时候,int就不再适用了,此时就需要使用long long,防止数据溢出。
如果有兴趣了解更多知识,这里给大家推荐一个网站:
另外,如果坚持要使用int的话,建议使用公式:c = a + (b - a)/2;
因为noj提供的测试样例最多只允许一次误差(整型数据类型强行取整,去除小数部分)
005:进制转换

基础知识回顾: %X(十六进制大写),%x(十六进制小写), %o(八进制)

#include <stdio.h>
int main(){
unsigned int n;
scanf("%d", &n);
printf("%X,%o", n, n);
return 0;
}
// 这里其实最好来说“%d”应该替换为“%u”,更为严谨。
006:浮点数输出

#include <stdio.h>
int main(){
double n;
scanf("%lf", &n);
printf("%.6lf,%.2lf,%.8lf", n, n, n);
return 0;
}
007:动态宽度输出
知识点:“%0md”,不足m位,高位用0补齐

#include <stdio.h>
int main() {
int m, n;
scanf("%d %d", &m, &n);
printf("%0*d\n", n, m);
return 0;
}
// 此处星号表示宽度(即补0个数)将由参数n提供
008: 计算地球上两点距离


需要注意的点:
1.math.h库里的三角函数的参数均为弧度制,而题目要求的输入的经纬度是角度,需要乘pi/180
2.样例输出里有km单位,所以printf里也要带上km
3.cos(pi)= -1, arccos(-1)= pi。 const double pi = acos(-1); //用这句来提供pi的精确值
#include <stdio.h>
#include <math.h> // 包含三角函数计算
const double pi = acos(-1); // pi 值
const double t = pi / 180.0; // 用于将角度转换为弧度的常量
// 计算 haversine 函数
double hav(double theta){
double h = (1.0 - cos(theta)) / 2.0;
return h;
}
int main(){
double lat1, lon1, lat2, lon2; // 分别表示两点的纬度和经度
const double r = 6371.0; // 地球半径,单位为公里
double d;
// 输入两点的经纬度(以度为单位)
scanf("%lf %lf", &lat1, &lon1);
scanf("%lf %lf", &lat2, &lon2);
// 将经纬度转换为弧度
lat1 *= t;
lon1 *= t;
lat2 *= t;
lon2 *= t;
// 使用 Haversine 公式计算球面距离
double hav_lat = hav(lat2 - lat1); // 纬度差的 haversine
double hav_lon = hav(lon2 - lon1); // 经度差的 haversine
d = 2 * r * asin(sqrt(hav_lat + cos(lat1) * cos(lat2) * hav_lon)); // 计算距离
// 输出距离,保留4位小数
printf("%.4lfkm", d);
return 0;
}
009:风寒指数


#include <stdio.h>
#include <math.h>
int main(){
double v,t;
scanf("%lf %lf",&v,&t);
double result=13.12+0.6215*t-11.37*pow(v,0.16)+0.3965*t*pow(v,0.16);
printf("%.0lf",result);
}
按照公式编写代码即可,这里涉及到了pow(底数,指数)函数的使用
另外%.0lf表示保留到整数位,%.lf保留小数点后一位, %.mf保留小数点后m位
注意,%.mf不会改变存储在参数中的值,只是在输出的时候四舍五入后显示在屏幕上(有的参考书中认为是“四舍六入五成双”(视编译器而定),在大物实验中要用到,统计学中的银行家舍入法)
四舍六入五成双是一种比较精确比较科学的计数保留法,是一种数字修约规则。这里“四舍”是指≤4时舍去,“六入”是指≥6时进上,“五成双”指的是根据5后面的数字来定,当5后有数时,舍5入1;当5后无有效数字时,需要分两种情况来讲:①5前为奇数,舍5入1;②5前为偶数,舍5不进。
若想改变参数的值以便在后续使用,可以利用round(double x)函数(四舍五入到整数位),
需注意printf时要用%.0lf或使用%d和(int)x进行强制类型转换
#include <stdio.h>
#include <math.h>
int main(){
double v,t;
scanf("%lf %lf",&v,&t);
double result=13.12+0.6215*t-11.37*pow(v,0.16)+0.3965*t*pow(v,0.16);
result = round(result);
printf("%d",(int)result);
}
010:颜色模型转换


这里需要注意的东西不多,记住fmax和fmin两个math库函数即可,参数只能是两个。
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main()
{
double H, S, V, MIN, MAX;
double R, G, B;
scanf("%lf %lf %lf", &R, &G, &B);
R = R * 100.0; G = G * 100.0; B = B * 100.0;
V = fmax(R, G);
V = fmax(V, B);
MAX = V;
V = MAX / 255.0;
MIN = fmin(R, G);
MIN = fmin(MIN, B);
if (V == 0) {
S = 0;
} else {
S = 100.0 * (MAX - MIN) / MAX;
}
if (MAX == R) {
H = 0 + 60.0 * ((G - B) / (MAX - MIN));
} else if (MAX == G) {
H = 120.0 + 60.0 * ((B - R) / (MAX - MIN));
} else if (MAX == B) {
H = 240.0 + 60.0 * ((R - G) / (MAX - MIN));
}
if (H < 0) {
H = H + 360.0;
}
printf("%.4lf, %.4lf%%, %.4lf%%\n", H, S, V);
}
011: 操作数(各位数字之和)
这里使用while循环比for循环更直观,更容易编写。
#include <stdio.h>
long long solve(long long n){
long long result = 0;
while(n>0){
result = result + n%10;
n=n/10;
}
return result;
}
int main(){
long long n;
scanf("%lld", &n);
long long num=0;
while(n>0){
n=n-solve(n);
num++;
}
printf("%lld\n", num);
}
012:方阵

#include <stdio.h>
int main(){
long long n,k,j;
scanf("%lld",&n);
if(n==0){
printf("0\n");
}
else{
for(long long i=0;i<n;i++){
for(k=i;k>0;k--){
printf("%lld ",k);// 如j循环,对称打印
}
for(j=0;j<n-1-i;j++){ //输入5,第1行为0-4;输入n,第一行为0-(n-1);i为行数,一共n行序数,第一行对应i=0.
printf("%lld ",j);
}
printf("%lld\n",j);// 此时j=n-1-i,打印后换下一行
}
}
return 0;
}
013:幂数模

#include <stdio.h>
int main(){
long long a,b,m;
scanf("%lld %lld %lld", &a, &b, &m);
long long result=1;
while(b!=0){
if(b%2){
result=(result*a)%m;
}
a=(a*a)%m;
b=b/2;
}
printf("%lld\n", result);
}
PS:如果觉得频繁使用long long打字麻烦,可以使用typrdef
其实这道题如果使用暴力循环的话代码是下面这个样子:
for (unsigned long long i = 0; i < b; i++) {
result = (result * a) % m;
}
这里必须用long long,但也只能达到2^63-1的数据范围,而且两个变量相乘的话很有可能溢出,如果使用unsigned long long,数据范围达到0~2^64-1,则应该不会溢出,但是O(b)的复杂度在b(幂次)如此大的情况下就难以接受了(一般OJ系统无法承受如此大的运算量)
这里用到了下面的模运算法则:主要是乘法结合律

每次乘法后立即取模,不会改变最终结果,同时大大减少了中间结果的大小,可以防止溢出
溢出的问题我们解决了,那么为了降低时间复杂度,我们可以像题解一样使用快速幂算法(也称二分幂),时间复杂度可降至O(logb),下面就来简单介绍一下这个算法:(本题解是快速幂的迭代写法,另外还有递归写法,感兴趣的读者可以自行查阅)


014:组合数
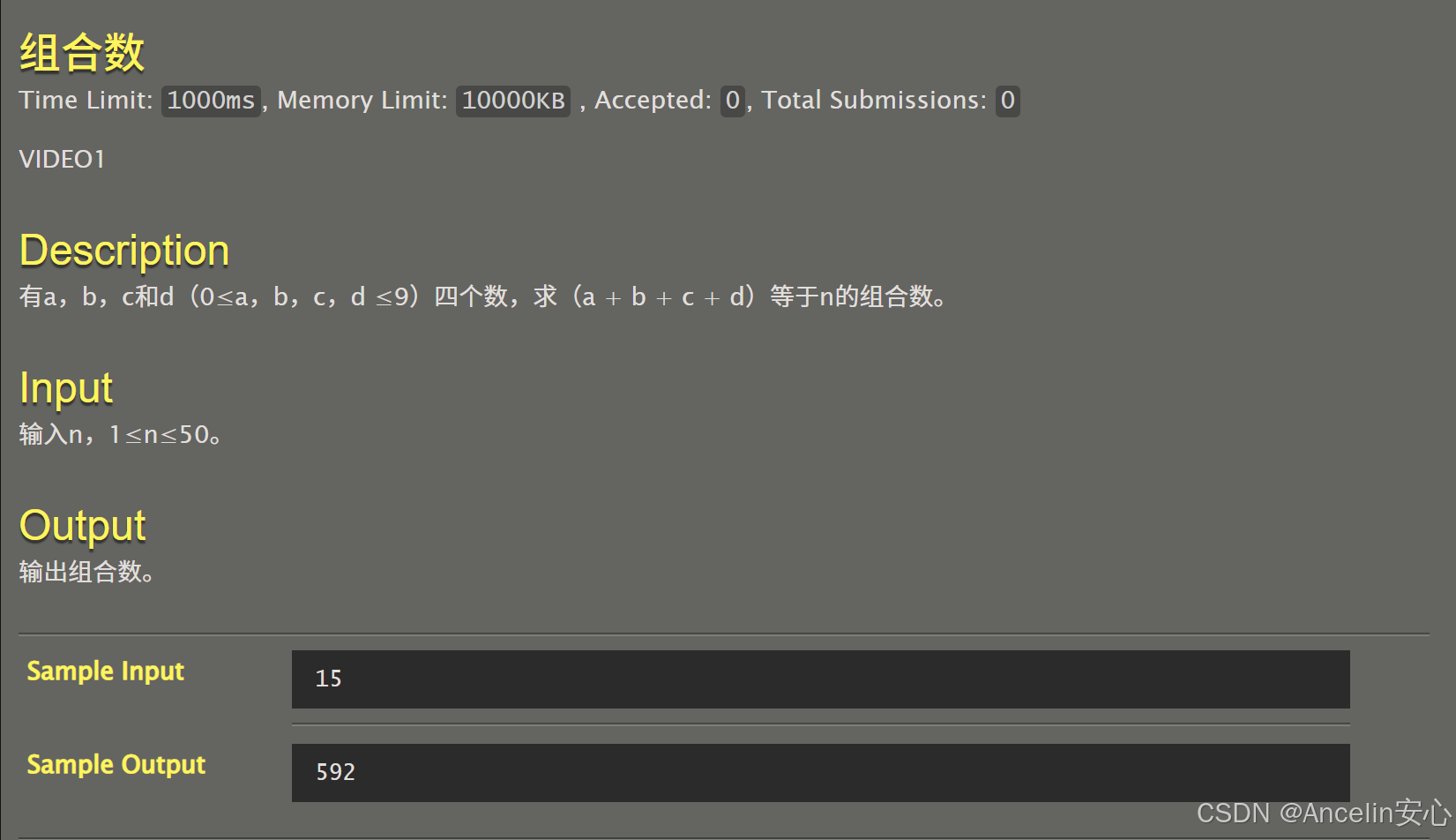
题解1:暴力循环法
#include <stdio.h>
int main(){
int n;
int sum=0;
scanf("%d",&n);
for(int i=0;i<=9;i++)
for(int j=0;j<=9;j++)
for(int k=0;k<=9;k++)
for(int x=0;x<=9;x++){
if(i+j+k+x==n){
sum++;
}
}
printf("%d",sum);
}
题解2:利用数学和逻辑

#include <stdio.h>
int main() {
int n;
int sum = 0;
scanf("%d", &n);
for (int i = 0; i <= 9; i++) {
for (int j = 0; j <= 9; j++) {
for (int k = 0; k <= 9; k++) {
int x = n - (i + j + k);
if (x >= 0 && x <= 9) {
sum++;
}
}
}
}
printf("%d", sum);
return 0;
}
题解3 :动态规划
想要更深入了解的读者可以移步至:告别动态规划,连刷40道动规算法题,我总结了动规的套路-CSDN博客
#include <stdio.h>
int count_combinations(int n) {
int dp[51] = {0}; // 定义 dp 数组,大小为 n + 1,初始化为 0
dp[0] = 1; // 和为 0 的情况初始化为 1,其他为 0
// 进行 4 次循环,分别表示选择 a, b, c, d
for (int count = 0; count < 4; count++) {
for (int x = n; x >= 0; x--) {
for (int i = 1; i <= 9; i++) {
if (x - i >= 0) {
dp[x] += dp[x - i];
}
}
}
}
return dp[n];
}
int main() {
int n;
scanf("%d", &n); // 输入 n 的值,1 <= n <= 50
printf("%d\n", count_combinations(n)); // 输出结果
return 0;
}
015:对称数

首先,题目印错了,是旋转180°
然后,这道题要找出所有特殊数字:1,8,0只需要和自身成对出现;9,6必须互相成对出现。成对指横坐标互为相反数。如果位数为奇数,中间的数只能是1,8,0这三个数。
最后,这道题要用到求位数的代码,读者可自行积累:
求整数位数:
int num,digit=0;
while(num)
{
digit++;
num = num/10;
}完整题解:
#include<stdio.h>
int GetFigure(int a){
int count=0;
do{
count++;
a/=10;
}
while(a!=0);{
return count;
}
}//获取一个数字有几位
void GetFigureToStorage(int a,int arr[],int b){
for(int i=0;i<b;i++){
arr[i]=a%10;
a/=10;
}
}//获取一个数字的各个位数,并存在数组里
int YesOrNo(int arr[],int a){
int count=0;
if(a%2==1){
if(arr[(a+1)/2-1]==1||arr[(a+1)/2-1||arr[(a+1)/2-1]==8]==0){
for(int i=0;i<a;i++){
if(arr[i]==6&&arr[a-i-1]==9){
{
count++;
}
}
if(arr[i]==9&&arr[a-i-1]==6)
{
count++;
}
if(arr[i]==1){
count++;
}
if(arr[i]==0){
count++;
}
if(arr[i]==8){
count++;
}
count++;
}
}
}
if(a%2==0){
for(int j=0;j<a;j++){
if(arr[j]==6&&arr[a-j-1]==9){
{
count++;
}
}
if(arr[j]==9&&arr[a-j-1]==6)
{
count++;
}
if(arr[j]==1){
count++;
}
if(arr[j]==0){
count++;
}
if(arr[j]==8){
count++;
}
}
}
return count;
}
int main(){
int a;
int arr1[32];
int flag=0;
scanf("%d",&a);
int b;
b=GetFigure(a);
GetFigureToStorage( a, arr1, b);
int m;
m=YesOrNo(arr1,b);
if((b%2==0&&m==b)||(b%2==1&&m==2*b))
{
printf("Yes");
}
else{
printf("No");
}
}016:分数的加、减、乘、除法

很明显我们要用到最大公约数和化最简分数的知识,我们来学习一下:
1.最大公约数:欧几里得算法(辗转相除法)
名字听起来高大上,实际上记住一个定理就OK(证明过程很简单,感兴趣的读者可以去查阅)
定理(递归式):gcd(a,b) = gcd(b,a%b) 其中,gcd(a,b)表示a和b的最大公约数
递归边界:gcd(a,0) = a
求解最大公约数:
int gcd(int a, int b){
return !b ? a : gcd(b, a%b);
}2.分数的化简:

有了最大公约数和分数化简的知识,我们就可以实现分数的四则运算了:
#include <stdio.h>
#include <string.h>
//求最大公约数
int gcd(int x,int y){
if(y==0){
return x;
}
return gcd(y,x%y);
}
int main(){
int a1,a2,b1,b2;
int result1,result2,common_divisor;
scanf("%d/%d",&a1,&a2);
scanf("%d/%d",&b1,&b2);
//加法
result1=a1*b2+a2*b1;
result2=a2*b2;
common_divisor=gcd(result1,result2);
result1/=common_divisor;
result2/=common_divisor;
printf("(%d/%d)+(%d/%d)=%d/%d\n",a1,a2,b1,b2,result1,result2);
//减法
result1=a1*b2-a2*b1;
result2=a2*b2;
common_divisor=gcd(result1,result2);
result1/=common_divisor;
result2/=common_divisor;
printf("(%d/%d)-(%d/%d)=%d/%d\n",a1,a2,b1,b2,result1,result2);
//乘法
result1=a1*b1;
result2=a2*b2;
common_divisor=gcd(result1,result2);
result1/=common_divisor;
result2/=common_divisor;
printf("(%d/%d)*(%d/%d)=%d/%d\n",a1,a2,b1,b2,result1,result2);
//除法
result1=a1*b2;
result2=a2*b1;
common_divisor=gcd(result1,result2);
result1/=common_divisor;
result2/=common_divisor;
printf("(%d/%d)/(%d/%d)=%d/%d\n",a1,a2,b1,b2,result1,result2);
return 0;
}
017:乘数模
依照以上定理,有如下代码:(此题无需使用循环)
#include<stdio.h>
typedef long long LL;
int main(){
LL a, b, m,result;
scanf("%lld", &a);
scanf("%lld", &b);
scanf("%lld", &m);
result = (a%m)*(b%m)%m;
printf("%lld", result);
return 0;
}
018:级数和

这里尤其要注意样例输出格式,由于题目告诉了我们n的范围(不会超过两位数),所以我们可以分两种情况(一位数还是两位数)来保留不同的小数位数 (除以10还是除以100),但是最后‘=’的右边结果保留几位小数我们不确定样例是怎么给的,比如1.2+2.3=3.5还是3.50?
此外还要注意‘+’的个数及位置。
还有9.1并没有输出为9.10,可见当i+1为整十整百时要把小数末尾的0去掉。
平时做题时我们可以根据判题结果来判断,但是考试是OI赛制(即看不到任何作答正确与否的反馈),我们如果不确定的话需要举手询问老师。
这里经过测试,是始终保留两位小数,如果是动态保留小数位数的话,请读者参考:
C语言根据输入n来保留n位小数_c保留小数点后n位-CSDN博客
简单来说,就是“%.*lf”
另外,关于编程竞赛赛制有兴趣的小伙伴可以移步☞:
【划重点】编程比赛三大赛制你了解吗? (ACM赛制、OI赛制、IOI赛制)_提交看不到分数是什么赛制-CSDN博客
题解1:
#include <stdio.h>
int main() {
int n;
double sum = 1.2;
scanf("%d", &n);
printf("1.2");
for (int i = 2; i <= n; i++) {
if((i+1)%10==0)
{
printf("+%d.%d", i, (i+1)/10);
}
else{
printf("+%d.%d", i, i + 1);
}
if(i>=9){
sum+=i+((double)(i+1))/100.0;
}
else{
sum+=i+((double)(i+1))/10.0;
}
}
printf("=%.2lf\n", sum);
return 0;
}
题解2:(适用于n更大的范围,大约10^9以内,如果超过,要用long long)
#include<stdio.h>
#include<math.h>
int main(){
int i,j,n,digit=1;
double sum=1.2;
scanf("%d", &n);
printf("1.2");
for(i=2;i<=n;i++){
j=i+1;
digit=0;
while(j){
digit++;
j = j/10;
}
sum+=i+((double)i+1)/pow(10,digit);
if((i+1)%10==0) printf("+%d.%d", i,(int)((i + 1)/pow(10,digit-1)));
else printf("+%d.%d", i, i + 1);
}
printf("=%.*lf",digit,sum);
return 0;
}
019:比率(小数化分数)

这里由于不知道样例数据的精度,使用long long最为稳妥。
#include<stdio.h>
#include<math.h>
typedef long long L;
L gcd(L a, L b){
return !b ? a : gcd(b, a%b);
}
int main(){
double n;
L x,common_divisor,base=100000000000;
scanf("%lf", &n);
n=n*base;//这里乘多少要看样例的精度
x=n;
common_divisor=gcd(x,base);
x/=common_divisor;
base/=common_divisor;
printf("%lld/%lld", x, base);
return 0;
}
020:倍数和(malloc使用,等差数列求和,放任上溢出)

题解1: (AC)
#include <stdio.h>
long long sum_of_multiples(long long n) {
n--;
long long sum3 = (n / 3) * (3 + (n / 3) * 3) / 2;
long long sum5 = (n / 5) * (5 + (n / 5) * 5) / 2;
long long sum15 = (n / 15) * (15 + (n / 15) * 15) / 2;
return sum3 + sum5 - sum15;
}
int main(){
long long T,n;
scanf("%lld",&T);
int arr[100000];
for(long long i=0;i<T;i++){
scanf("%lld",&n);
//printf("%lld\n",solve(n));
//printf("%lld\n",sum_of_multiples(n));
arr[i]=sum_of_multiples(n);
}
for(long long i=0;i<T;i++){
printf("%lld\n",arr[i]);
}
}
题解2:(WA,逻辑没问题,原因是系统样例可能放任了上溢出)
#include <stdio.h>
#include <stdlib.h>
// 计算小于 n 的所有 x 的倍数之和
long long sum_of_multiples(long long n, long long x) {
long long count = (n - 1) / x;
return x * count * (count + 1) / 2;
}
int main() {
int t;
scanf("%d", &t); // 读取测试用例数量
long long *n = (long long *)malloc(t * sizeof(long long)); //动态获取内存
for (int i = 0; i < t; i++) {
scanf("%lld", &n[i]); // 读取每个测试用例的值
}
for (int i = 0; i < t; i++) {
long long result = sum_of_multiples(n[i], 3)
+ sum_of_multiples(n[i], 5)
- sum_of_multiples(n[i], 15);
printf("%lld\n", result);
}
return 0;
}021:余数和

#include<stdio.h>
#include<math.h>
int main(){
int n,k,i,sum=0;
scanf("%d%d", &n,&k);
for(i=1;i<=n;i++){
sum+=(k%i);
}
printf("%d", sum);
return 0;
}
注意sum初始化一定要赋值,否则随机分配的值结果肯定不对。
022:毕达哥拉斯三元组(放任上溢出)

这道题有点类似014:组合数,可以通过求差的方式求最后一个变量,减少循环层数,而前两层循环是典型的枚举思路。
#include<stdio.h>
#include<math.h>
int main(){
int n,c,i,j;
scanf("%d", &n);
for(i=1;i<n/3;i++){
for(j=2;j<n/2;j++){
c=n-j-i;
if(i*i+j*j==c*c){
long long result=i*j*c;
printf("%lld", result);
}
}
}
return 0;
}
023:好数字(快速幂,分类讨论)

这里一定要注意题目要求,输入的n不是直接拿来判断是否是好数字的 ,而是位数是n的所有数判断是否为好数字,统计个数。下面的代码就是搞错了这一点。
#include<stdio.h>
#include<math.h>
bool isPrime(long long n){
if(n<=1)return false;
for(long long i=2;i*i<=n;i++){
//long long型防止溢出
//此处也可以使用开根号
if(n%i==0)return false;
}
return true;
}
int getDigit(long long n){
int digit=0;
while(n){
digit++;
n=n/10;
}
return digit;
}
long long getBase(int digit){
digit*=(int)pow(10.0,digit);
return digit;
}
int main(){
long long n,digit,t,base,j,num=0;
scanf("%lld", &n);
digit=getDigit(n)-1;
j=(digit+1)/2+1;
base=getBase(digit);
for(int i=0;i<j;i++){
t=n/base;
if(t%2!=0)break;
n-=t*base;
base/=10;
t=n/base;
if(isPrime(!t))break;
n-=t*base;
base/=10;
}
printf("%lld", num%1000000007);
return 0;
}
下面是正确的代码,使用了013:幂数模提到的快速幂算法
题解1:
#include <stdio.h>
#define MOD 1000000007
// 快速幂算法,计算 base^exp % MOD
long long fastPow(long long base, long long exp, long long mod) {
long long result = 1;
while (exp > 0) {
if (exp % 2 == 1) {
result = (result * base) % mod;
}
base = (base * base) % mod;
exp /= 2;
}
return result;
}
int main() {
long long N;
scanf("%lld", &N);
// 偶数位置的个数和奇数位置的个数
long long evenCount = (N + 1) / 2; // 偶数位置
long long oddCount = N / 2; // 奇数位置
// 计算 5^evenCount % MOD 和 4^oddCount % MOD
long long evenChoices = fastPow(5, evenCount, MOD);
long long oddChoices = fastPow(4, oddCount, MOD);
// 结果为两者乘积 % MOD
long long result = (evenChoices * oddChoices) % MOD;
printf("%lld\n", result);
return 0;
}

题解2:
#include <stdio.h>
#include <math.h>
int main(){
long long n;
scanf("%lld",&n);
long long sum=1;
long long mod=pow(10,9);
mod+=7;
for(long long i=0;i<n;i++){
if(i%2==0)
sum=(sum*5)%mod;
else
sum=(sum*4)%mod;
}
printf("%lld\n",sum);
}
024:查找数列 (等差数列求和)

#include<stdio.h>
#include<math.h>
int main(){
int n,i,num;
scanf("%d", &n);
for(i=1;i<=n;i++){
if(i*(i+1)/2>n)break;
}
num=n-(i-1)*i/2;
printf("%d", num);
return 0;
}
通过等差数列求和公式确定n在哪个区域里,n与左边界差值即为数列中第n个数字。

025: 阶乘倍数(n!)

这里我们回顾一下n!的计算方法:采用递归的思想
int F(int n){
if(n==0)return 1;
else return F(n-1)*n;
}但是递归对于较大的输入 n,代码会导致 整数溢出,无法求解比12!更大的阶乘,换成long long也只能求解到20!
如果读者对求解更大阶乘感兴趣的话(其实就是大数运算)
可以参考:C语言入门与进阶——求n的阶乘_c语言求n的阶乘-CSDN博客
这时我们可以采取质因子分解的方法:

#include <stdio.h>
// 计算一个数的质因数分解
void primeFactorize(long long k, long long primes[], long long exponents[], int *size) {
*size = 0;
for (long long p = 2; p * p <= k; p++) {
if (k % p == 0) {
primes[*size] = p;
exponents[*size] = 0;
while (k % p == 0) {
exponents[*size] += 1;
k /= p;
}
(*size)++;
}
}
if (k > 1) { // 如果剩余一个大质数
primes[*size] = k;
exponents[*size] = 1;
(*size)++;
}
}
// 计算 N! 中包含的某个质因数的总数
long long countPrimeInFactorial(long long n, long long p) {
long long count = 0;
while (n > 0) {
count += n / p;
n /= p;
}
return count;
}
// 主函数
int main() {
long long k;
scanf("%lld", &k);
// 对 k 进行质因数分解
long long primes[64], exponents[64];
int size;
primeFactorize(k, primes, exponents, &size);
// 对每个质因数找到满足条件的最小 N
long long result = 0;
for (int i = 0; i < size; i++) {
long long p = primes[i], e = exponents[i];
long long n = 0, low = 1, high = k;
// 二分搜索最小的 N
while (low <= high) {
long long mid = (low + high) / 2;
if (countPrimeInFactorial(mid, p) >= e) {
n = mid;
high = mid - 1;
} else {
low = mid + 1;
}
}
// 更新结果为所有质因数对应的最大 N
if (n > result) {
result = n;
}
}
printf("%lld\n", result);
return 0;
}
还有相对简单的解法:
#include <stdio.h>
#include <math.h>
int judge(int num){
for(int i=2;i<sqrt(num);i++){
if(num%i==0){
return 1;
}
}
return 0;
}
int main(){
long long k;
scanf("%lld",&k);
long long sum=1;
long long n=2;
if(judge(k)==0&&k>20)
{
printf("%lld\n",k);
}
else{
while(1){
sum=sum*n;
//printf("%lld\n",sum);
if(sum%k==0){
printf("%lld\n",n);
break;
}
n++;
}
}
return 0;
}026:竖式乘法(获取整数各位)

#include<stdio.h>
int getDigit(int n){
int digit=0;
while(n){
digit++;
n/=10;
}
return digit;
}
int main(){
int a,b,result=0;
scanf("%d %d", &a, &b);
result=a*b;
int len=getDigit(result);
printf("%*d\n",len+1,a);
printf("x%*d\n",len,b);
for(int i=0;i<=len;i++){
printf("-");
}
printf("\n");
int l=len+1,t;
while(b){
t=(b%10)*a;
printf("%*d\n",l,t);
b/=10;
if(b>0&&b<10)printf("+"),l-=1;
l--;
}
for(int i=0;i<=len;i++){
printf("-");
}
printf("\n");
printf(" %d",result);
return 0;
}
这里注意:系统测试样例中a和b应该是非0的,或者没有给有0的情况单独讨论,此程序面对b=0时会有以下输出:(但是不影响AC)

另外通过此题我们应该积累求整数位数getDigit()和获取整数各位的方法(num%10,num/=10)
027: 倒水(DFS)


这里会用到深度优先搜索(DFS),感兴趣的读者可以移步至:第十三章 DFS与BFS(保姆级教学!!超级详细的图示!!)_dfs bfs-CSDN博客
#include <stdio.h>
#include <math.h>
#define MAX 101
int m,n,d;
int min_steps=-1;
int used[MAX][MAX]={0};
void dfs(int x,int y,int steps){
//若找到符合条件,则进行比较,找最小操作数
if(x==d||y==d){
if(steps <min_steps||min_steps==-1)
min_steps=steps;
return;
}
//避免无限深搜,用数组标记搜索过的样例
if(used[x][y]==1){
return;
}
used[x][y]=1;
//倒空一个杯子
dfs(0,y,steps+1);
dfs(x,0,steps+1);
//装满一个杯子
dfs(m,y,steps+1);
dfs(x,n,steps+1);
//把水从x倒入y里
int sum=x+y;
int x_next,y_next;
if(sum>n){
x_next=sum-n;
y_next=n;
}
else{
x_next=0;
y_next=sum;
}
dfs(x_next,y_next,steps+1);
//把水从y倒入x里
if(sum>m){
x_next=m;
y_next=sum-m;
}
else{
x_next=sum;
y_next=0;
}
dfs(x_next,y_next,steps+1);
used[x][y]=0;
}
int main(){
scanf("%d %d %d",&m,&n,&d);
dfs(0,0,0);
printf("%d\n",min_steps);
}
028:方案数(t=n,j=i)

#include<stdio.h>
#include<math.h>
int getDigit(int n){
int digit=0;
while(n){
digit++;
n/=10;
}
return digit;
}
int main(){
int n,num=1,i,j;
scanf("%d", &n);
for(i=n-1;i>=1;i--){
int t=n;
for(j=i;j>=1;j--){
t-=j;
if(t<0)break;
if(t==0)num++;
}
}
printf("%d",num);
return 0;
}
这里要注意设置一个临时变量t代替n进行运算,新一轮循环时更新t的值为n的初值 。
029:俄罗斯农夫乘法


此题有时间限制,直接使用乘法 会导致超时:RE


1.634s>1s,超时,使用加法可以降低运行时间
#include <stdio.h>
int main() {
int a,b,result;
scanf("%d %d", &a, &b);
result=a*b;//投机取巧
printf("%d %d\n", a, b);
while(a!=1){
a>>=1;
b<<=1;
printf("%d %d\n", a, b);
}
printf("%d", result);
}
下面为正解:注意使用long long防止溢出
#include <stdio.h>
int main() {
long long a,b,sum=0;
scanf("%lld %lld", &a, &b);
while(a>0){
printf("%lld %lld\n", a, b);
if(a%2){
sum+=b;
}
a>>=1;
b<<=1;
}
printf("%lld", sum);
}
030:最大数字

题目的意思是结果的各位数字从左到右单调不减 ,如199的1,9,9就是顺序不递减
题解1:由于要对n的各位进行比较,可以采用字符数组的数据结构
#include <stdio.h>
#include <string.h>
void findMax(char *n) {
int len = strlen(n);
int flag = 0; // 标记从哪里开始需要将数字置为9
// 从右往左遍历,寻找递减的地方
for (int i = len - 1; i > 0; i--) {
if (n[i] < n[i - 1]) { // 出现递减
n[i - 1]--; // 前一位数字减1
flag = i; // 标记需要将当前位及后面的位变为9
}
}
if(flag){
// 将标记位及之后的数字都设置为'9'
for (int i = flag; i < len; i++) {
n[i] = '9';
}
}
printf("%s", n);
}
int main() {
char n[20];
scanf("%s", n);
findMax(n);
return 0;
}题解2:通过mod10获取各位数字
#include <stdio.h>
int judge(int num){
int t1=9;
while(num>0){
int t2=num%10;
num/=10;
if(t1<t2){
return 0;
}
t1=t2;
}
return 1;
}
int main(){
int n;
scanf("%d",&n);
for(int i=n;i>=0;i--){
if(judge(i)){
printf("%d\n",i);
break;
}
}
}
031:可变参数累加

#include <stdio.h>
#include <stdarg.h>
int sum(int a,...){
va_list args;
va_start(args, a);
int result = 0;
result+=a;
int next;
while(next=va_arg(args, int)){
result+=next;
}
return result;
}
int main(){
int a,b,c,d,e,f;
scanf("%d %d %d %d %d %d", &a , &b , &c , &d , &e , &f);
int result=sum(a,b,0)-sum(c,d,e,f,0);
printf("%d\n", result);
}032:佩尔数(递归或递推)



#include <stdio.h>
int PB(int n){
int p0=0,p1=1,pn,i;
for(i=0;i<=n;i++)
if(i==0) pn=p0;
else if(i==1) pn=p1;
else{
pn=2*p1+p0;
p0=p1;
p1=pn;
}
return pn;
}
int PA(int n){
if(n==0) return 0;
else if(n==1) return 1;
if(n%2){
return 2*PB(n-1)+PA(n-2);
}
else{
return 2*PA(n-1)+PB(n-2);
}
}
int pell(int n){
if(n%2)
return PA(n);
else
return PB(n);
}
int main(){
int n;
scanf("%d",&n);
printf("%d\n",pell(n));
}
033:素数

#include<stdio.h>
#include<math.h>
int judge(int n){
for(int i=2;i<=sqrt(n);i++){
if(n%i==0)return 0;
}
return 1;
}
int main(){
int a,b,i,num=0;
scanf("%d%d", &a, &b);
for(i=a;i<=b;i++){
if(judge(i))num++;
}
printf("%d", num);
return 0;
}本题题干向我们介绍了三种判断素数的方式,第一种为全范围枚举,第二种为开根号,第三种为埃氏筛,045题会要求我们使用第四种:欧拉筛 。一般情况下,这四种算法的效率递增。
034:可变参数平均

#include <stdio.h>
#include <stdarg.h>
double avg(int n,...){
va_list args;
va_start(args, n);
double result = 0.0;
for (int i = 0; i < n; i++) {
result += va_arg(args, double);
}
va_end(args);
return result/n;
}
int main(){
double a,b,c,d,e;
scanf("%lf %lf %lf %lf %lf", &a, &b, &c, &d, &e);
double result=avg(2,a,b)-avg(3,c,d,e);
printf("%.4lf\n", result);
}035: 冰雹序列


#include<stdio.h>
#include<math.h>
int ice(int n){
while(n!=1){
if(n%2==0)n/=2;
else n=n*3+1;
printf(" %d", n);
}
}
int main(){
int n;
scanf("%d", &n);
printf("%d", n);
ice(n);
}
036:哈沙德数 (函数递归调用)

 写代码一定要注意边界值检验,否则可能出现死循环 。
写代码一定要注意边界值检验,否则可能出现死循环 。
#include <stdio.h>
inline int HSD(int n){
int t=n,s=0;
while(t){
s+=t%10;
t/=10;
}
if(s && n%s==0)return n/s;
return 0;
}
int main() {
int n,num=0,t;
scanf("%d", &n);
t=HSD(n);
while(t>1){
num++;
t=HSD(t);
}
if(t==1)num++;
printf("%d", num);
}
核心点是要用到函数递归的思想。
037: 基思数(num->数组+逆序复制)

#include <stdio.h>
int lsKeith(int N) {
int len = 0;
int originalN = N;
int sequence[100];
int a[100];
int sum=0;
while(N>0){
sequence[len++] = N%10;
N=N/10;
}
int index=0;
for(int i=len-1; i>=0; i--){
a[index++]=sequence[i];
sum+=sequence[i];
}
int start=0;
while(1){
a[index++]=sum;
sum=sum+sum-a[start++];
if(sum==originalN){
return 1;
}
if(sum>originalN){
return 0;
}
}
return 0;
}
int main() {
int N;
scanf("%d", &N);
if (lsKeith(N) == 1) {
printf("Yes\n");
} else {
printf("No\n");
}
}
038:光线追踪


#include <stdio.h>
long long calculateTotalLength(long long N, long long X) {
long long totalLength = N;
long long N_X=N-X;//镜墙
while(N_X>0){
if(N_X%X==0){//镜墙的长度刚好可以让一种光长的光线反射到原点
long long n=N_X/X;
totalLength+=(2*n-1)*X;
break;
}
else if(N_X/X>=1){//不能,则需要计算差多少,最后置换反射光长和镜墙的长度
long long n=N_X/X;
totalLength+=2*n*X;
int tmp=N_X-X*n;
N_X=X;
X=tmp;
}
}
return totalLength;
}
int main() {
long long N, X;
scanf("%lld %lld", &N, &X);
long long totalLength;
if(N-X>=X)
totalLength=calculateTotalLength(N, X);
else
totalLength=calculateTotalLength(N, N-X);
printf("%lld\n", totalLength);
return 0;
}
039:二进制表示

#include <stdio.h>
void binaryRepresentation(int n) {
if (n == 0) {
return;
} else if (n == 1) {
printf("2(0)");
} else if (n == 2) {
printf("2");
} else {
int power = 0;
int temp = 1;
while (temp * 2 <= n) {
temp *= 2;
power++;
}
if (temp == n) {
printf("2(");
binaryRepresentation(power);
printf(")");
} else {
if(power == 1) {//括号内的单独为1的数字不需要转换为2(0)
printf("2+");
}
else{
printf("2(");
binaryRepresentation(power);
printf(")+");
}
binaryRepresentation(n - temp);
}
}
}
int main() {
int n;
scanf("%d", &n);
binaryRepresentation(n);
printf("\n");
return 0;
}
040:运动会


#include <stdio.h>
#include <math.h>
// 计算欧拉函数
int eulerTotient(int n) {
int result=n; // 初始化结果为 n
// 遍历从 2 到 sqrt(n) 的所有质数
for (int i=2; i<=sqrt(n);i++) {
// 如果 i 是 n 的因子
if (n%i == 0) {
// 不断除以 i,直到它不再是 n 的因子
while (n%i == 0) {
n/=i;
}
// 更新结果
result-=result/i;
}
}
// 如果 n 是一个大于 1 的质数
if (n>1) {
result-=result/n;
}
return result;
}
int main(){
int n;
int sum=0;
scanf("%d",&n);
for(int i=0;i<n;i++){
sum+=eulerTotient(i);
}
sum=sum*2+1;
printf("%d\n",sum);
}
041:行列式值


这里介绍常见的两种方法:1.递归法(按第一行展开);2.高斯消元法(化简成上三角式)
1.递归法(适用于n较小的情况,时间复杂度为O(n!))
#include <stdio.h>
// 计算行列式的函数
int determinant(int n, int matrix[n][n]) {
//此为递归边界,如果样例中基础情况较多则代码执行效率会提高一些
// 基础情况:1x1 矩阵
if (n == 1) {
return matrix[0][0];
}
// 基础情况:2x2 矩阵
if (n == 2) {
return matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0];
}
//基础情况:3x3 矩阵(考试时可省略)
if (n == 3) {
return matrix[0][0] * matrix[1][1] * matrix[2][2]
+ matrix[0][1] * matrix[1][2] * matrix[2][0]
+ matrix[0][2] * matrix[1][0] * matrix[2][1]
- matrix[0][0] * matrix[1][2] * matrix[2][1]
- matrix[0][1] * matrix[1][0] * matrix[2][2]
- matrix[0][2] * matrix[1][1] * matrix[2][0];
}
//初始化行列式的值为0
int det = 0;
//第一层循环用来递归展开第一行
//第一层循环的col变量是为了遍历主矩阵第一行的各列元素
for (int col = 0; col < n; col++) {
// 创建一个子矩阵,由于规定展开第一行,所以只需要排除当前列即可
int submatrix[n-1][n-1];
//第二层循环用来给子矩阵赋值
//第二层循环的i变量是为了遍历子矩阵的行
for (int i = 1; i < n; i++) {
int subcol = 0;//此变量用来遍历子矩阵的列
for (int j = 0; j < n; j++) {
if (j != col) {//排除当前列
//将主矩阵的元素赋值(复制)给子矩阵
submatrix[i-1][subcol] = matrix[i][j];
subcol++;
}
}
}
// 递归计算子行列式
int subdet = determinant(n-1, submatrix);
// 加上当前元素与子行列式的乘积,循环后相当于求和公式
if (col % 2 == 0) {
//因从col=0开始循环,列数少了1,加上第一行的行数正好相等
//行数和列数求和为公式中(-1)的指数,和偶则加
det += matrix[0][col] * subdet;
} else {
det -= matrix[0][col] * subdet;//和奇则减
}
}
return det;
}
int main() {
int n;
// 输入矩阵的大小(阶数)
scanf("%d", &n);
// 输入矩阵的元素
int matrix[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
scanf("%d", &matrix[i][j]);
}
}
// 计算行列式
int result = determinant(n, matrix);
// 输出结果
printf("%d\n", result);
return 0;
}
2.高斯消元法 (适用于n较大的情况,时间复杂度为O(n^3))
此处我们可以汲取的营养有:1.如果寻找数组中的最大值;2.如何交换两个变量的值
#include <stdio.h>
#include <math.h>
// 计算行列式的高斯消元法
double determinant(int n, double matrix[n][n]) {
double det = 1;
for (int i = 0; i < n; i++) {
// 寻找当前列的最大元素并进行行交换
int maxRow = i;
for (int j = i + 1; j < n; j++) {
if (fabs(matrix[j][i]) > fabs(matrix[maxRow][i])) {
maxRow = j;
}
}
// 如果主元素为零,则行列式为零
if (matrix[maxRow][i] == 0) {
return 0;
}
// 交换行
if (maxRow != i) {
for (int j = 0; j < n; j++) {
double temp = matrix[i][j];
matrix[i][j] = matrix[maxRow][j];
matrix[maxRow][j] = temp;
}
// 每次交换行,行列式符号反转
det *= -1;
}
// 消元过程:通过当前行消去当前列下方的元素
for (int j = i + 1; j < n; j++) {
if (matrix[j][i] != 0) {
double factor = matrix[j][i] / matrix[i][i];
for (int k = i; k < n; k++) {
matrix[j][k] -= factor * matrix[i][k];
}
}
}
// 计算行列式时,乘上对角线元素
det *= matrix[i][i];
}
return det;
}
int main() {
int n;
// 输入矩阵的大小
scanf("%d", &n);
// 输入矩阵的元素
double matrix[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
scanf("%lf", &matrix[i][j]);
}
}
// 计算行列式
double result = determinant(n, matrix);
// 输出结果
printf("%.0lf\n", result);
return 0;
}
042:完美矩阵


#include <stdio.h>
#include <math.h>
int a[300][300];
int counts=0;
int is_perfect(int x1, int y1, int x2, int y2){
int zeros=0,ones=0;
for(int i=x1;i<=x2;i++)
for(int j=y1;j<=y2;j++){
if(i==x1||i==x2||j==y1||j==y2){
if(a[i][j]!=1){
return 0;
}
}
else{
if(a[i][j]==0){
zeros++;
}
else{
ones++;
}
}
}
if(abs(zeros-ones)<=1){
return 1;
}
else{
return 0;
}
}
void sums(int n,int m){
int MIN=fmin(n,m);
for(int k=MIN;k>1;k--){
for(int i=0;i<n-k+1;i++)
for(int j=0;j<m-k+1;j++){
if(k==2){
int x1=i,x2=i+k-1,y1=j,y2=j+k-1;
if(a[x1][y1]==1&&a[x1][y2]==1&&a[x2][y1]==1&&a[x2][y2]==1){
counts++;
}
}
else if(is_perfect(i,j,i+k-1,j+k-1)){
counts++;
}
}
}
}
int main(){
int n,m;
scanf("%d %d",&n,&m);
for(int i=0;i<n;i++)
for(int j=0;j<m;j++){
scanf("%d",&a[i][j]);
}
sums(n,m);
printf("%d\n",counts);
return 0;
}
043: 货运优化


#include <stdio.h>
int main(){
int a[7];
int a_3[4]={0,5,3,1};
while(1){
scanf("%d %d %d %d %d %d",&a[1],&a[2],&a[3],&a[4],&a[5],&a[6]);
if(a[1]==0&&a[2]==0&&a[3]==0&&a[4]==0&&a[5]==0&&a[6]==0){
break;
}
int sum=0;
sum+=a[6];
sum+=a[5];
sum+=a[4];
int sub=a[2]-a[4]*5;
sum+=a[3]/4;
if(a[3]%4){
sum++;
}
int x=a_3[a[3]%4];
if(sub>=0){
if(a[2]-sub>x){
sum+=(a[2]-sub-x)/9;
if((a[2]-sub-x)%9){
sum++;
}
}
}
x=36*sum-(a[3]*9+a[2]*4+a[4]*16+a[5]*25+a[6]*36);
if(a[1]>x){
sum+=(a[1]-x)/36;
if((a[1]-x)%36){
sum++;
}
}
printf("%d\n",sum);
}
return 0;
}044:【专业融合:管理】航空旅行

#include <stdio.h>
int main(){
int n;
scanf("%d",&n);
int a[3];
int d,e;
for(int i=0;i<n;i++){
int flag=0;
scanf("%d %d %d %d %d",&a[0],&a[1],&a[2],&d,&e);
for(int j=0;j<2;j++)
for(int k=0;k<2-j;k++){
if(a[k]>a[k+1])
{
int tmp=a[k];
a[k]=a[k+1];
a[k+1]=tmp;
}
}
if(a[2]+a[1]<=d&&a[0]<=e){
flag=1;
}
if(flag) printf("YES\n");
else printf("NO\n");
}
}
045:素数筛选法(介绍埃氏筛,使用欧拉筛)




#include <stdio.h>
#define N 10000000
int vis[N+1]={0};
int pr[N+1];//存质数
int cnt=0;
void Euler_sieve(int n)
{
int i,j;
for(i=2;i<=n;i++){
if(vis[i]==0){
pr[cnt++]=i;
}
for(j=0;j<cnt;j++){
if(i*pr[j]>n)//超出范围停止
break;
vis[i*pr[j]]=1;
if(i%pr[j]==0)//找到最小质因子后停止搜索
break;
}
}
}
int main(){
int n;
scanf("%d",&n);
Euler_sieve(n);
printf("%d\n",cnt);
return 0;
}
046:回文数之和

#include <stdio.h>
int is_palindrome(int num){
int source=num;
int result=0;
while(num>0){
result=result*10+num%10;
num=num/10;
}
if(source==result) return 1;
return 0;
}
int convert(int num,int k){
int result=0;
int base=1;
while(num>0){
result=result+(num%k)*base;
num=num/k;
base*=10;
}
return result;
}
int main() {
int n,k;
scanf("%d %d",&n,&k);
int sum=0;
for(int i=1;i<n;i++){
if(is_palindrome(i)&&is_palindrome(convert(i,k)))
sum+=i;
}
printf("%d\n",sum);
return 0;
}
047:【专业融合:计算机】波士顿房价预测(最小二乘法)



#include <stdio.h>
//最小二乘法
struct point{
int x;
int y;
};
int main(){
int n;
scanf("%d",&n);
struct point arr[n];
double sum_x=0,sum_y=0;
for(int i=0; i<n; i++){
scanf("%d %d",&arr[i].x,&arr[i].y);
sum_x+=arr[i].x;
sum_y+=arr[i].y;
}
double x_m=sum_x/n;
double y_m=sum_y/n;
double a=0,b=0;
double tmp1,tmp2;
for(int i=0; i<n; i++){
tmp1+=(arr[i].x-x_m)*(arr[i].y-y_m);
tmp2+=(arr[i].x-x_m)*(arr[i].x-x_m);
}
b=tmp1/tmp2;
a=y_m-b*x_m;
printf("Y=%.4lf+%.4lf*X",a,b);
}
对最小二乘法感兴趣的读者可以移步至:一文让你彻底搞懂最小二乘法(超详细推导)-CSDN博客
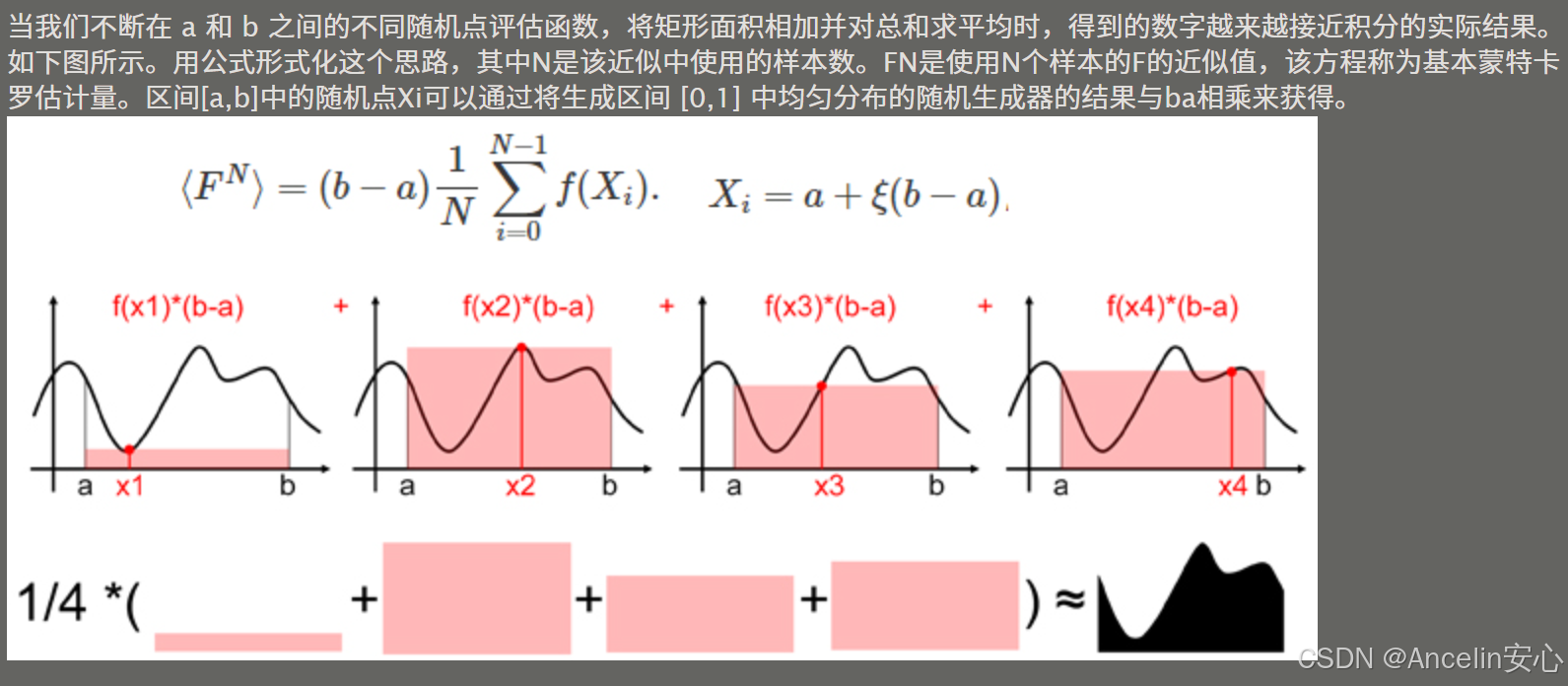
048:【专业融合:物理】蒙特卡洛方法求积分





#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(){
int m,N;
double a,b;
scanf("%d %lf %lf %d",&m,&a,&b,&N);
srand(RAND_MAX);
double sum=0;
double result;
if(m==1){
for(int i=0;i<1999;i++){
double randomValue=a + ((double)rand() / RAND_MAX) * (b - a);
double x1=pow(randomValue,4);
double x2=exp(-randomValue);
sum+=x1*x2;
}
result=(b-a)*sum/N;
}
else if(m==2){
for(int i=0;i<1999;i++){
double randomValue=a + ((double)rand() / RAND_MAX) * (b - a);
sum+=pow(randomValue,2)+1;
}
result=(b-a)*sum/N;
}
else if(m==3){
for(int i=0;i<1999;i++){
double randomValue=a + ((double)rand() / RAND_MAX) * (b - a);
sum+=cos(randomValue);
}
result=(b-a)*sum/N;
}
else if(m==4){
for(int i=0;i<1999;i++){
double randomValue=a + ((double)rand() / RAND_MAX) * (b - a);
sum+=pow(randomValue,0.5)*(randomValue-2);
}
result=(b-a)*sum/N;
}
else if(m==5){
for(int i=0;i<1999;i++){
double randomValue=a + ((double)rand() / RAND_MAX) * (b - a);
sum+=2*sin(randomValue)-5*cos(randomValue);
}
result=(b-a)*sum/N;
}
printf("%.6lf\n", result);
}049:稀疏矩阵

#include <stdio.h>
int main() {
int n, m;
scanf("%d %d", &n, &m);
int matrix[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
scanf("%d", &matrix[i][j]);
}
}
int non_zero_count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (matrix[i][j] != 0) {
non_zero_count++;
}
}
}
if (non_zero_count <= 0.05 * n * m || non_zero_count == n || non_zero_count == m) {
printf("Yes\n");
} else {
printf("No\n");
}
return 0;
}
050:【专业融合:航空】飞机起飞速度



#include <stdio.h>
#include <math.h>
#define scanf scanf_s
double calculateSpeed(double temperature, double pressure, int elevation, int runway, int weight, int flaps, int wet) {
// 检查输入是否在有效范围内
if (flaps != 1 && flaps != 5 && flaps != 15) {
return -1;
}
if (weight < 41413 || weight > 65000 || runway <= 6900) {
return -1;
}
// 计算温度档和气压档
int tempRange = floor(temperature / 10);
int pressureRange = ceil(pressure);
// 检查操纵参考表是否存在
if (tempRange < 0 || tempRange > 7 || pressureRange < 0 || pressureRange > 9) {
return -1;
}
// 根据温度档和气压档查找操纵参考值
char referenceTable[8][10] = {
{'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'J', 'K'},
{'L', 'M', 'N', 'P', 'Q', 'R', 'S', 'T', 'U', 'V'},
{'W', 'X', 'Y', 'Z', 'A', 'B', 'C', 'D', 'E', 'F'},
{'G', 'H', 'J', 'K', 'L', 'M', 'N', 'P', 'Q', 'R'},
{'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', 'A', 'B'},
{'C', 'D', 'E', 'F', 'G', 'H', 'J', 'K', 'L', 'M'},
{'N', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X'},
{'Y', 'Z', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'}
};
char reference = referenceTable[tempRange][pressureRange];
// 检查操纵参考表是否存在V1、Vr和V2
if (reference != 'A' && reference != 'B' && reference != 'C' && reference != 'D' && reference != 'E') {
return -1;
}
// 根据襟翼位置、起飞重量和操纵参考值查找V1、Vr和V2
int speedTable[3][5] = {
{117, 126, 134, 142, 151},
{122, 131, 139, 147, 156},
{127, 136, 145, 153, 162}
};
int speedIndex = (flaps - 1) / 7;
int* speedRow = speedTable[speedIndex];
int v1 = speedRow[weight / 13000];
int vr = speedRow[weight / 13000] + 11;
int v2 = speedRow[weight / 13000] + 18;
// 如果是湿跑道,根据跑道长度和襟翼位置查找折扣值
if (wet == 1) {
int discountTable[3][3] = {
{0, 0, 0},
{0, 0, 0},
{0, 0, 0}
};
int discountIndex = (flaps - 1) / 7;
int* discountRow = discountTable[discountIndex];
int discount = discountRow[runway / 1000];
v1 -= discount;
}
printf("V1=%dkts Vr=%dkts V2=%dkts\n", v1, vr, v2);
return 0;
}
int main() {
double temperature, pressure;
int elevation, runway, weight, flaps, wet;
scanf("%lf %lf", &temperature, &pressure);
scanf("%d %d %d %d %d", &elevation, &runway, &weight, &flaps, &wet);
int result = calculateSpeed(temperature, pressure, elevation, runway, weight, flaps, wet);
if (result == -1) {
printf("Flight not possible!\n");
}
return 0;
}//读者可当做练习,自行检查上述代码中的无效代码行,发表在评论区 (本题可能WA)
字符串部分推荐使用C++的STL,会简单很多。
下面是string类常用函数介绍:

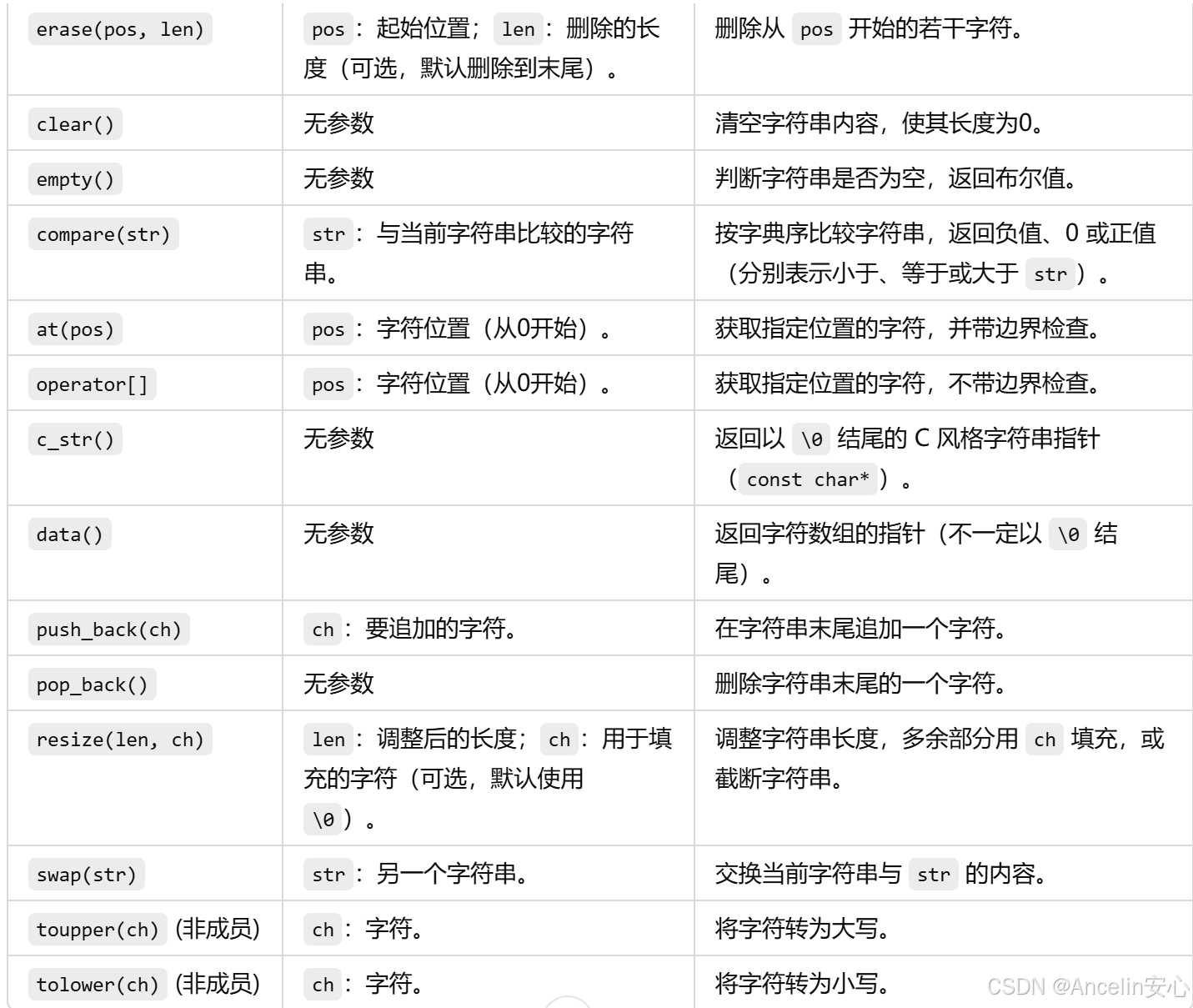
有兴趣深入学习的读者可移步至:【C++ STL】string类最全解析(什么是string?string类的常用接口有哪些?)-CSDN博客
//C语言string库的常用函数会在后文介绍
//从51题往后,部分题目可能难度很大,需要一定的数学知识支持(如计算方法这门课学到的牛顿迭代法),对数学证明感兴趣的读者可以移步至:2024年NOJ详解(51-80)-CSDN博客
051:删除前后缀

#include <bits/stdc++.h>
using namespace std;
void str_removeprefix(string str,string words){
while(str.compare(0,words.length(),words)==0&&str.length()>=words.length()){
str.erase(0,words.length());
}
cout << str << endl;
}
void str_removesuffix(string str,string words){
while(str.compare(str.length()-words.length(),words.length(),words)==0&&str.length()>=words.length()){
str.erase(str.length()-words.length());
}
cout << str << endl;
}
int main(){
string str,words;
getline(cin,str);
getline(cin,words);
str_removeprefix(str,words);
str_removesuffix(str,words);
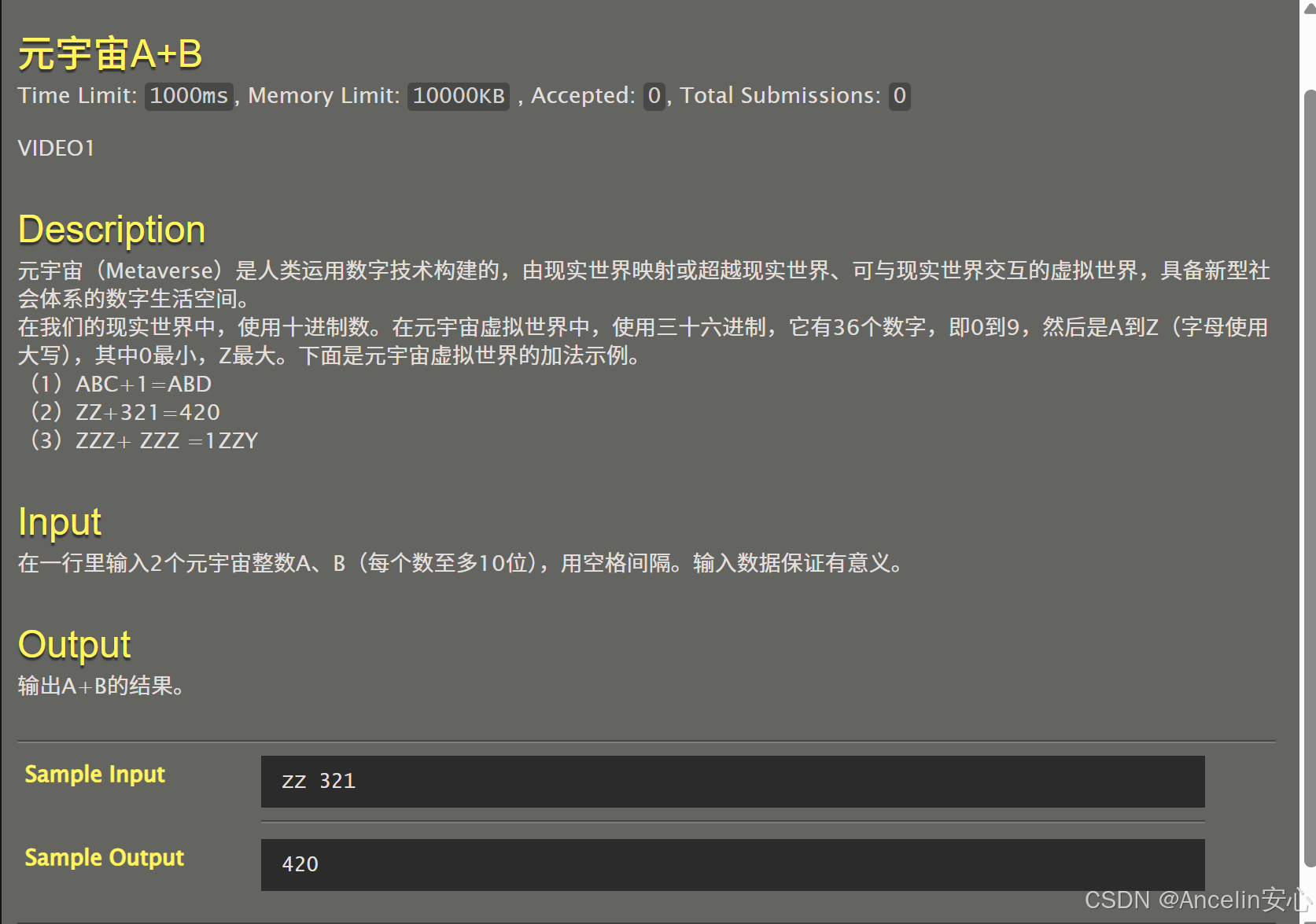
}052:元宇宙A+B (36进制运算)
#include <stdio.h>
#include <string.h>
int charToValue(char c) {
if (c >= '0' && c <= '9') {
return c - '0'; // 将 '0'-'9' 转换为 0-9
}
return c - 'A' + 10; // 将 'A'-'Z' 转换为 10-35
}
char valueToChar(int value) {
if (value < 10) {
return '0' + value; // 将 0-9 转换回 '0'-'9'
}
return 'A' + (value - 10); // 将 10-35 转换回 'A'-'Z'
}
int main() {
char A[15], B[15];
scanf("%s %s", A, B);
long long a = 0, b = 0;
int lenA = strlen(A), lenB = strlen(B);
// 将 A 从36进制转换为十进制
for (int i = 0; i < lenA; i++) {
a = a * 36 + charToValue(A[i]);
}
// 将 B 从36进制转换为十进制
for (int i = 0; i < lenB; i++) {
b = b * 36 + charToValue(B[i]);
}
// 计算十进制的和
long long sum = a + b;
// 将和转换回36进制
char result[15];
int index = 0;
if (sum == 0) {
result[index++] = '0'; // 处理和为0的情况
} else {
while (sum > 0) {
result[index++] = valueToChar(sum % 36);
sum /= 36;
}
}
// 反转结果以得到正确的顺序
for (int i = index - 1; i >= 0; i--) {
printf("%c", result[i]);
}
printf("\n");
return 0;
}
053:大小写交换

#include <bits/stdc++.h>
using namespace std;
void str_swapcase(string &str){
for(int i=0; i<str.length();i++){
if(str[i]>='A'&&str[i]<='Z'){
str[i]+='a'-'A';
}
else if(str[i]>='a'&&str[i]<='z'){
str[i]-='a'-'A';
}
}
}
int main(){
string str;
getline(cin, str);
str_swapcase(str);
cout << str <<endl;
}
小写字母比大写字母的ASCII码值大32,代码中使用'a'-'A'同理,在做ASCII码值运算(整型运算时)要采用单引号''
getline()是C++中接受字符串输入的函数,参数cin,str(存储的字符串)
054: 分离字符串

#include <bits/stdc++.h>
using namespace std;
void str_split(string str,string sep){
while(1){
int pos=str.find(sep);
if(pos==-1){
cout<<str<<endl;
break;
}
else{
cout<<str.substr(0,pos)<<endl;
str=str.substr(pos+sep.length());
}
}
}
int main(){
string str,sep;
getline(cin,str);
getline(cin,sep);
str_split(str,sep);
}
这里我们学习一下两个函数:
1.str.find(sep):
- 在字符串
str中查找分隔符sep的位置,返回第一个匹配的位置索引。 - 如果找不到分隔符,则返回
-1。
2.str.substr(pos, len) 用来提取子字符串
返回从 pos 开始、长度为 len 的子字符串,len默认为到字符串末尾。
055:字符串后缀

#include <bits/stdc++.h>
using namespace std;
int str_endswith(string str,string suffix){
if(str.length()<suffix.length()) return 0;
int len=str.length()-suffix.length();
str.erase(0,len);
if(str==suffix)
return 1;
return 0;
}
int main(){
string str,suffix;
getline(cin, str);
getline(cin, suffix);
if(str_endswith(str, suffix))
cout<<"Yes"<<endl;
else
cout<<"No"<<endl;
}str.erase(pos,len)删除从pos开始,长度为len的字符串部分
056:字符串替换(WA,系统问题目前无法AC)


样例输入输出都正常,但是评判系统始终WA,也试过C++,结果还是WA,空格和str不存在olds的情况都考虑到了,这道题解的代码看看思路即可,顺便复习一下C语言字符串常用函数:

#include <stdio.h>
#include <string.h>
void str_replace(char *str, const char *olds, const char *news) {
char buffer[2001]; // 临时存储替换后的字符串
char *pos; // 指向匹配位置的指针
int old_len = strlen(olds); // olds 的长度
int new_len = strlen(news); // news 的长度
buffer[0] = '\0'; // 初始化 buffer
while ((pos = strstr(str, olds)) != NULL) {
// 将当前字符串中的非匹配部分复制到 buffer
strncat(buffer, str, pos - str);
// 将 news 替换 olds
strcat(buffer, news);
// 更新 str 指针到下一个位置
str = pos + old_len;
}
// 拼接剩余的字符串部分
strcat(buffer, str);
// 输出替换后的字符串
printf("%s\n", buffer);
}
int main() {
char str[1001], olds[101], news[101];
// 输入字符串
fgets(str, 1001, stdin);
str[strcspn(str, "\n")] = '\0'; // 去掉换行符
fgets(olds, 101, stdin);
olds[strcspn(olds, "\n")] = '\0'; // 去掉换行符
fgets(news, 101, stdin);
news[strcspn(news, "\n")] = '\0'; // 去掉换行符
// 调用替换函数
str_replace(str, olds, news);
return 0;
}
057:Kids A+B(两位数加法)

#include <bits/stdc++.h>
using namespace std;
map<string, int> numberMap = {
{"zero", 0}, {"one", 1}, {"two", 2}, {"three", 3}, {"four", 4},
{"five", 5}, {"six", 6}, {"seven", 7}, {"eight", 8}, {"nine", 9},
{"ten", 10}, {"eleven", 11}, {"twelve", 12}, {"thirteen", 13},
{"fourteen", 14}, {"fifteen", 15}, {"sixteen", 16}, {"seventeen", 17},
{"eighteen", 18}, {"nineteen", 19}, {"twenty", 20}, {"thirty", 30},
{"forty", 40}, {"fifty", 50}, {"sixty", 60}, {"seventy", 70},
{"eighty", 80}, {"ninety", 90}
};
map<int,string> enmap={
{0,"zero"},{1,"one"},{2,"two"},{3,"three"},
{4,"four"},{5,"five"},{6,"six"},{7,"seven"},
{8,"eight"},{9,"nine"},{10,"ten"},{11,"eleven"},
{12,"twelve"},{13,"thirteen"},{14,"fourteen"},{15,"fifteen"},
{16,"sixteen"},{17,"seventeen"},{18,"eighteen"},{19,"nineteen"},
{20,"twenty"},{30,"thirty"},{40,"forty"},{50,"fifty"},{60,"sixty"},
{70,"seventy"},{80,"eighty"},{90,"ninety"}
};
int convert(string a){
int num;
int pos=a.find('-');
if(pos!=-1){
string x=a.substr(0,pos);
string y=a.substr(pos+1);
num=numberMap[x]+numberMap[y];
}
else{
num=numberMap[a];
}
return num;
}
void convert_E(int a){
//cout<<"a:"<<a<<endl;
int x=a/10;
int y=a%10;
//cout<<x<<" "<<y<<endl;
if(x>1&&y)
cout<<enmap[x*10]<<"-"<<enmap[y]<<endl;
else if(x>=1)
cout<<enmap[a]<<endl;
else
cout<<enmap[y]<<endl;
}
int main(){
string a,b;
int num_a,num_b;
cin>>a>>b;
num_a=convert(a);
num_b=convert(b);
int res=num_a+num_b;
convert_E(res);
}058:Atol转换

#include <bits/stdc++.h>
using namespace std;
int Atol(string str){
long long res=0;
int len = str.length();
int sign = 1;
int i=0;
while(str[i]==' '){
i++;
}
if(str[i]=='+'){
sign=1;
i++;
}
else if(str[i]=='-'){
sign=-1;
i++;
}
while(str[i]>='0' && str[i]<='9'){
res=res*10+(str[i]-'0');
if(res*sign>INT_MAX) return INT_MAX;
if(res*sign<INT_MIN) return INT_MIN;
i++;
}
return res*sign;
}
int main(){
string str;
getline(cin,str);
cout<<Atol(str)<<endl;
}
059:前后缀移除

#include <bits/stdc++.h>
using namespace std;
void str_lstrip(string& str, string& chars) {
int pos = str.find_first_not_of(chars);
if (pos != string::npos) {
str.erase(0, pos);
}
}
void str_rstrip(string& str, string& chars) {
int pos = str.find_last_not_of(chars);
if (pos != string::npos) {
str.erase(pos + 1);
}
}
void str_strip(string& str, string& chars) {
str_lstrip(str, chars);
str_rstrip(str, chars);
}
int main() {
string str;
string chars;
string tmp;
getline(cin, str);
tmp=str;
getline(cin, chars);
str_lstrip(str, chars);
cout << str << endl;
str=tmp;
str_rstrip(str, chars);
cout << str << endl;
str=tmp;
str_strip(str, chars);
cout << str << endl;
return 0;
}
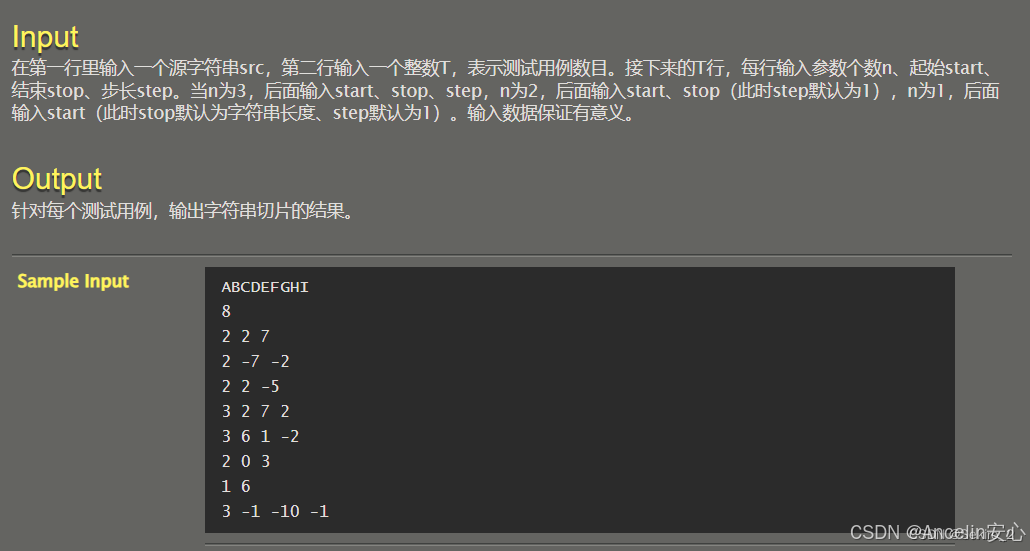
060: 字符串切片


#include <bits/stdc++.h>
using namespace std;
void str_slice(string src,int start,int stop,int step){
string res="";
if(start<0)
start=src.length()+start;
if(stop<0)
stop=src.length()+stop;
if(stop>=start)
for (int i = start; i < stop; i += step) {
res += src[i];
}
else
for (int i = start; i > stop; i += step) {
res += src[i];
}
cout<<res<<endl;
}
int main() {
string src;
cin >> src;
int t;
cin >> t;
for (int i = 0; i < t; ++i) {
int n;
cin >> n;
int start, stop, step;
if (n == 3) {
cin >> start >> stop >> step;
} else if (n == 2) {
cin >> start >> stop;
step = 1;
} else if (n == 1) {
cin >> start;
stop = src.length();
step = 1;
}
str_slice(src, start, stop, step);
}
return 0;
}
061:有效表达式(卡特兰数,dp)

题解1:

#include <stdio.h>
unsigned long int catalan(unsigned int n) {
if (n <= 1) return 1;
unsigned long int c = 0;
for (int i=0; i<n; i++)
c += catalan(i)*catalan(n-i-1);
return c;
}
int main() {
int n;
scanf("%d",&n);
printf("%d",catalan(n));
return 0;
}题解2:动态规划
#include<stdio.h>
long long catalanDP(long long n) {
long long dp[n+1];
dp[0] = dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = 0;
for (int j = 0; j < i; j++) {
dp[i] += dp[j] * dp[i-j-1];
}
}
return dp[n];
}
int main() {
long long n;
scanf("%lld", &n);
printf("%lld", catalanDP(n));
return 0;
}
062:【专业融合:通信】GPS通讯协议

#include <bits/stdc++.h>
using namespace std;
string out[100];
int k=0;
int check(string str){
int i,result;
for(result=str[1],i=2;str[i]!='*';i++)
{
result^=str[i];
}
return result;
}
int convert(string str){
int res=0;
res=stoi(str,0,16);
//cout<<res<<endl;
return res;
}
void convert_BeingTime(string utcTime){
int hour=stoi(utcTime.substr(0,2));
int B_hour=(hour+8)%24;
if(B_hour/10==0)
out[k++]="0"+to_string(B_hour)+":"+utcTime.substr(2,2)+":"+utcTime.substr(4,2);
else
out[k++]=to_string(B_hour)+":"+utcTime.substr(2,2)+":"+utcTime.substr(4,2);
}
int main(){
string str;
while(cin>>str){
if(str=="END") break;
if(str.compare(0,6,"$GPRMC")==0){
size_t asteriskPos = str.find('*');
if(asteriskPos!=string::npos){
int checksum=check(str);
int senchecksum=convert(str.substr(asteriskPos + 1, 2));
if(checksum!=senchecksum) {
out[k++]="error";
}
else{
// 提取UTC时间字段
string utcTime = str.substr(7, 6);
convert_BeingTime(utcTime);
}
}
}
}
for(int i=0;i<k;i++){
cout<<out[i]<<endl;
}
}
063:时钟A-B

#include <stdio.h>
#include <time.h>
int main() {
int yearA, monthA, dayA;
scanf("%d %d %d", &yearA, &monthA, &dayA);
int yearB, monthB, dayB;
scanf("%d %d %d", &yearB, &monthB, &dayB);
// 构建tm结构体表示A和B的日期时间
struct tm timeA = {0};
struct tm timeB = {0};
timeA.tm_year = yearA - 1900;
timeA.tm_mon = monthA - 1;
timeA.tm_mday = dayA;
timeB.tm_year = yearB - 1900;
timeB.tm_mon = monthB - 1;
timeB.tm_mday = dayB;
time_t timestampA = mktime(&timeA);
time_t timestampB = mktime(&timeB);
double difference = difftime(timestampA, timestampB);
printf("%.6lf\n", difference);
return 0;
}
064:【专业融合:电子】Arduino显示



#include <stdio.h>
int a[10]={6,2,5,5,4,5,6,3,7,6};
int convert(int x){
int res=0;
if(x==0) return a[x];
while(x){
res+=a[x%10];
x=x/10;
}
return res;
}
int calculate(int n){
n=n-4;
int sum=0;
for(int i=0; i<=2000;i++)
for(int j=0;j<=2000;j++){
int m=i+j;
if(convert(i)+convert(j)+convert(m)==n) {
//printf("%d+%d=%d\n",i,j,m);
sum++;
}
}
return sum;
}
int main(){
int n;
scanf("%d", &n);
printf("%d\n", calculate(n));
}
065:【专业融合:建筑】长安



#include <stdio.h>
int bx,by,px,py;
int sum=0;
int next[2][2]={{0,1},{1,0}};
void calculate(int x,int y){
//printf("x: %d y: %d\n",x,y);
if(x==bx&&y==by){
sum++;
return ;
}
else{
for(int i=0;i<2;i++){
int x1=x+next[i][0];
int y1=y+next[i][1];
if((x1==px&&y1==py)||x1>bx||y1>by){
continue;
}
calculate(x1,y1);
}
}
}
int main(){
while(scanf("%d %d %d %d",&bx,&by,&px,&py)){
if(bx==0&&by==0&&px==0&&py==0){
break;
}
sum=0;
//初始坐标需要选择(1,1)
calculate(1,1);
printf("%d\n",sum);
}
}066:【专业融合:生物】DNA双螺旋结构




#include <stdio.h>
void print_dna1(){
printf(" AT \n");
printf(" T--A \n");
printf(" A----T \n");
printf("T------A\n");
printf("T------A\n");
printf(" G----C \n");
printf(" T--A \n");
printf(" GC \n");
}
void print_dna2(){
printf(" CG \n");
printf(" C--G \n");
printf(" A----T \n");
printf("A------T\n");
printf("T------A\n");
printf(" A----T \n");
printf(" A--T \n");
printf(" GC \n");
}
void print_dna3(){
printf(" AT \n");
printf(" C--G \n");
printf(" T----A \n");
printf("C------G\n");
printf("C------G\n");
printf(" T----A \n");
printf(" G--C \n");
printf(" AT \n");
}
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n/2;i++){
if(i%3==1) print_dna1();
else if(i%3==2) print_dna2();
else if(i%3==0) print_dna3();
}
return 0;
}
067:循环排序

#include <stdio.h>
int main(){
int n;
scanf("%d",&n);
int a[n];
for(int i=0; i<n; i++){
scanf("%d",&a[i]);
}
for(int j=0; j<n-1; j++){
int item= a[j];
int pos= j;
for(int i=j+1; i<n;i++){
if(a[i]<item) pos++;
}
if(pos==j) continue;
int tmp=a[pos];
a[pos]=item;
item=tmp;
while(pos!=j){
pos=j;
for(int k=j+1;k<n;k++){
if (a[k] < item) {
pos++;
}
}
while (item == a[pos]) {
pos++;
}
int temp = a[pos];
a[pos] = item;
item = temp;
}
}
for (int i = 0; i < n; ++i) {
printf("%d ", a[i]);
}
}068:【专业融合:网安】加密字串
#include <bits/stdc++.h>
using namespace std;
int main(){
string s;
int x;
cin>>s;
cin>>x;
int alphabet[26]={0};
for(int i=0;i<s.length();i++){
alphabet[s[i]-'a']++;
}
for(int i=0;i<s.length();i++){
char tmp;
if(alphabet[s[i]-'a']%2){
tmp=((int)(s[i]-x-'a')%26+26)%26+'a';
}
else{
tmp=((int)(s[i]+x-'a')%26+26)%26+'a';
}
s[i]=tmp;
}
cout<<s<<endl;
}
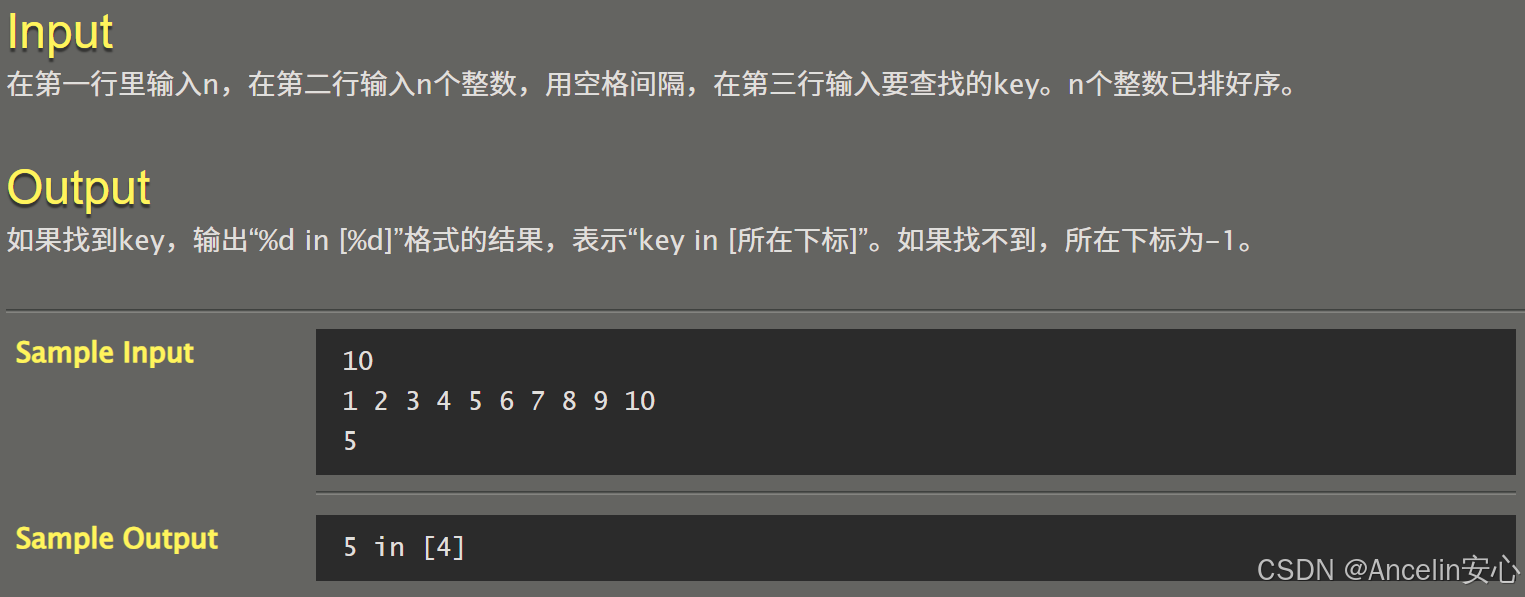
069:三元搜索


#include <stdio.h>
int main(){
int n;
scanf("%d",&n);
int a[n];
for(int i=0; i<n; i++){
scanf("%d",&a[i]);
}
int key;
scanf("%d",&key);
int left=0,right=n-1;
int mid1,mid2;
int result;
while(1){
if(key>a[right]){
result=-1;
break;
}
if(key<a[left]){
result=-1;
break;
}
mid1=left+(right-left)/3;
mid2=right-(right-left)/3;
if(a[mid1]==key)
{
result=mid1;
break;
}
if(a[mid2]==key)
{
result=mid2;
break;
}
if(mid1==mid2)
{
result=-1;
break;
}
if(key<a[mid1]) right=mid1-1;
else if(key>a[mid2]) left=mid2+1;
else if(key>a[mid1]&&key<a[mid2]){
left=mid1+1;
right=mid2-1;
}
}
printf("%d in [%d]",key,result);
}
070:【专业融合:自动化】PID控制
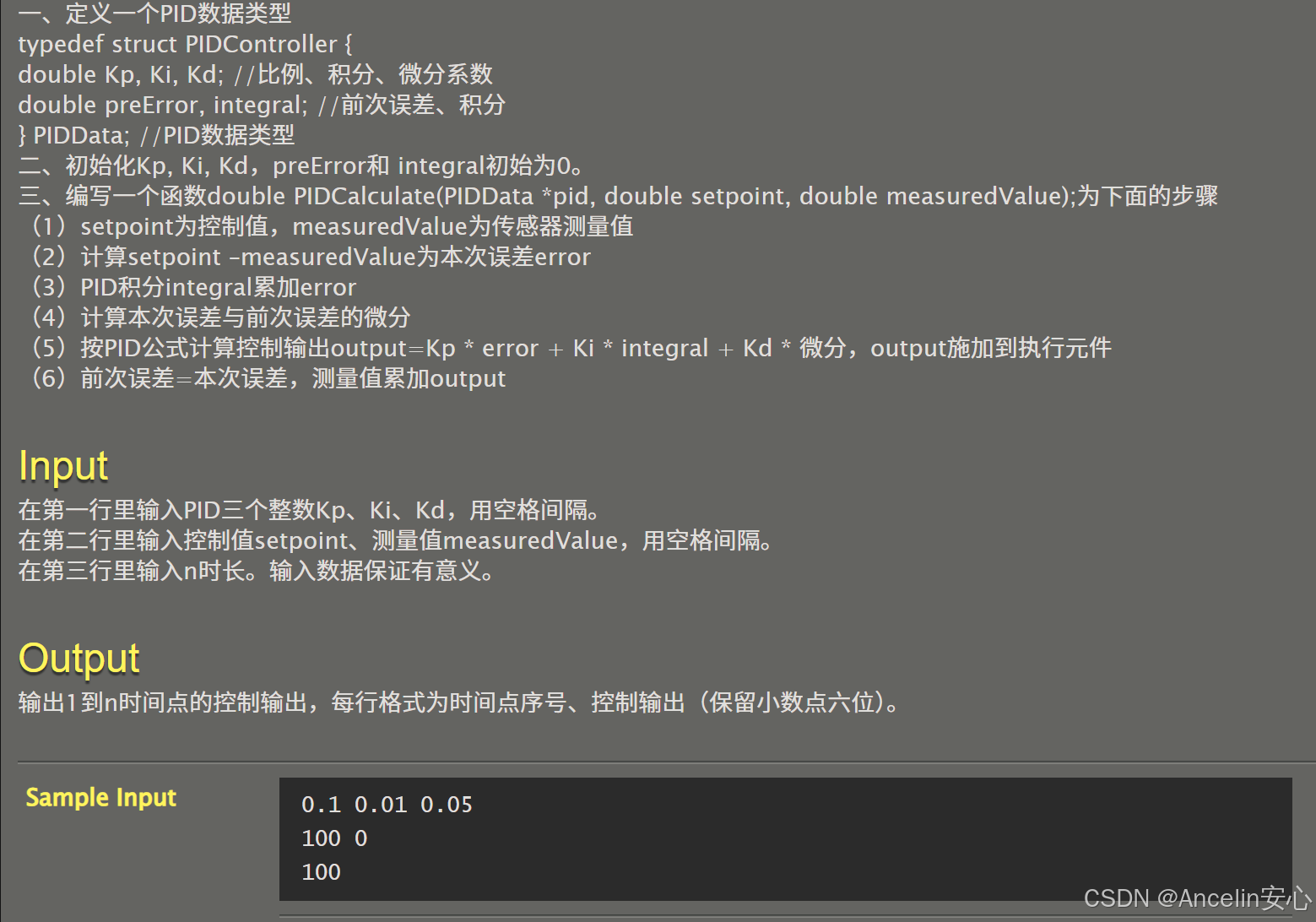

#include <stdio.h>
typedef struct PIDController{
double Kp,Ki,Kd;//比例、积分、微分系数
double preError,integral;//前次误差、积分
}PIDData;//PID数据类型
void PIDInit(PIDData *pid) {
pid->Kp = 0;
pid->Ki = 0;
pid->Kd = 0;
pid->preError = 0;
pid->integral = 0;
}
double PIDCalculate(PIDData *pid,double setpoint,double measuredValue){
double error=setpoint-measuredValue;
pid->integral+=error;
double diff=error-pid->preError;
pid->preError=error;
double output=pid->Kp*error+pid->Ki*pid->integral+pid->Kd*diff;
return output;
}
int main(){
double setpoint,measuredValue;
PIDData pid;
int n;
PIDInit(&pid);
scanf("%lf %lf %lf",&pid.Kp,&pid.Ki,&pid.Kd);
scanf("%lf %lf",&setpoint,&measuredValue);
scanf("%d",&n);
for(int i=1; i<=n;i++){
double output=PIDCalculate(&pid,setpoint,measuredValue);
//这里本应该打印ouput变量才对,但是noj上的输出是measuredValue
measuredValue+=output;
printf("%d %.6lf\n",i,measuredValue);
}
}
071:晶体密度




#include <bits/stdc++.h>
#include <cmath>
#include <math.h>
using namespace std;
struct Atom{
string name;
double mass;
double APF;//原子堆积因子
double r;//原子半径
};
Atom elemList[] =
{
{ "Po", 208.998, 0.52360, 1.68 },
{ "Li", 6.941, 0.68017, 1.52 },
{ "Na", 22.989770, 0.68017, 1.86 },
{ "Cr", 51.9961, 0.68017, 1.28 },
{ "Mn", 54.938049, 0.68017, 1.27 },
{ "Fe", 55.845, 0.68017, 1.26 },
{ "Mo", 95.94, 0.68017, 1.39 },
{ "Ta", 180.9749, 0.68017, 1.46 },
{ "Al", 26.981538, 0.74048, 1.43 },
{ "Ca", 40.078, 0.74048, 1.97 },
{ "Ni", 58.6934, 0.74048, 1.24 },
{ "Cu", 63.546, 0.74048, 1.28 },
{ "Ge", 72.64, 0.74048, 1.22 },
{ "Ag", 107.8682, 0.74048, 1.44 },
{ "Pt", 195.078, 0.74048, 1.39 },
{ "Au", 196.96655, 0.74048, 1.44 },
{ "Pb", 207.2, 0.74048, 1.75 }
};
int main(){
int n;
cin>>n;
string atoms;
for(int i=0; i<n; i++){
cin >> atoms;
for(int j=0;j<17;j++){
if(elemList[j].name==atoms){
double V=4.0/3.0*M_PI*pow(elemList[j].r,3);
double density=10.0*elemList[j].mass*elemList[j].APF/6.022/V;
printf("%.2lf\n",density);
break;
}
}
}
}072:几何约束

#include <stdio.h>
#include <math.h>
struct Point {
double x, y;
};
struct Segment {
struct Point start, end;
int index; // 线段的索引号
};
// 判断两线段是否相交
int doIntersect(struct Segment s1, struct Segment s2) {
double x1 = s1.start.x, y1 = s1.start.y;
double x2 = s1.end.x, y2 = s1.end.y;
double x3 = s2.start.x, y3 = s2.start.y;
double x4 = s2.end.x, y4 = s2.end.y;
double a1 = y2 - y1;
double b1 = x1 - x2;
double c1 = a1 * x1 + b1 * y1;
double a2 = y4 - y3;
double b2 = x3 - x4;
double c2 = a2 * x3 + b2 * y3;
double determinant = a1 * b2 - a2 * b1;
if (determinant == 0) {
// 平行线段
return 0;
} else {
double intersectX = (b2 * c1 - b1 * c2) / determinant;
double intersectY = (a1 * c2 - a2 * c1) / determinant;
// 检查交点是否在线段内
if (intersectX >= fmin(x1, x2) && intersectX <= fmax(x1, x2) &&
intersectX >= fmin(x3, x4) && intersectX <= fmax(x3, x4) &&
intersectY >= fmin(y1, y2) && intersectY <= fmax(y1, y2) &&
intersectY >= fmin(y3, y4) && intersectY <= fmax(y3, y4)) {
return 1;
} else {
return 0;
}
}
}
int main() {
int n;
scanf("%d", &n);
struct Segment segments[n];
// 读取线段信息
for (int i = 0; i < n; ++i) {
scanf("%lf %lf %lf %lf", &segments[i].start.x, &segments[i].start.y,
&segments[i].end.x, &segments[i].end.y);
segments[i].index = i + 1;
}
int intersectionCount = 0;
// 检查线段相交
for (int i = 0; i < n - 1; ++i) {
for (int j = i + 1; j < n; ++j) {
if (doIntersect(segments[i], segments[j])) {
printf("X: #%d #%d\n", segments[i].index, segments[j].index);
intersectionCount++;
}
}
}
// 输出相交的总数
printf("n=%d\n", intersectionCount);
return 0;
}073:【专业融合:航海】水下声学定位


#include <stdio.h>
#include <math.h>
#define PI 3.1415926
double solve_area(double AB,double BC,double CD,double DA,double diagonal){
double s_ABC = (AB + BC + diagonal)/2;
double s_ADC = (CD + DA + diagonal)/2;
double area_ABC = sqrt(s_ABC * (s_ABC - AB) * (s_ABC - BC) * (s_ABC - diagonal));
double area_ADC = sqrt(s_ADC * (s_ADC - CD) * (s_ADC - DA) * (s_ADC - diagonal));
return area_ABC +area_ADC;
}
double solve_angle(double AB,double BC,double CD,double DA,double diagonal,double area){
double angle=(4 *area )/(BC * BC + DA * DA - AB * AB - CD * CD);
return atan(angle)*180.0/PI;
}
int main(){
double ab,bc,cd,da,ac;
scanf("%lf %lf %lf %lf %lf",&ab,&bc,&cd,&da,&ac);
double area=solve_area(ab,bc,cd,da,ac);
double angle=solve_angle(ab,bc,cd,da,ac,area);
printf("%.6lf %.1lf",area,angle);
}074:【专业融合:化学】原子计数
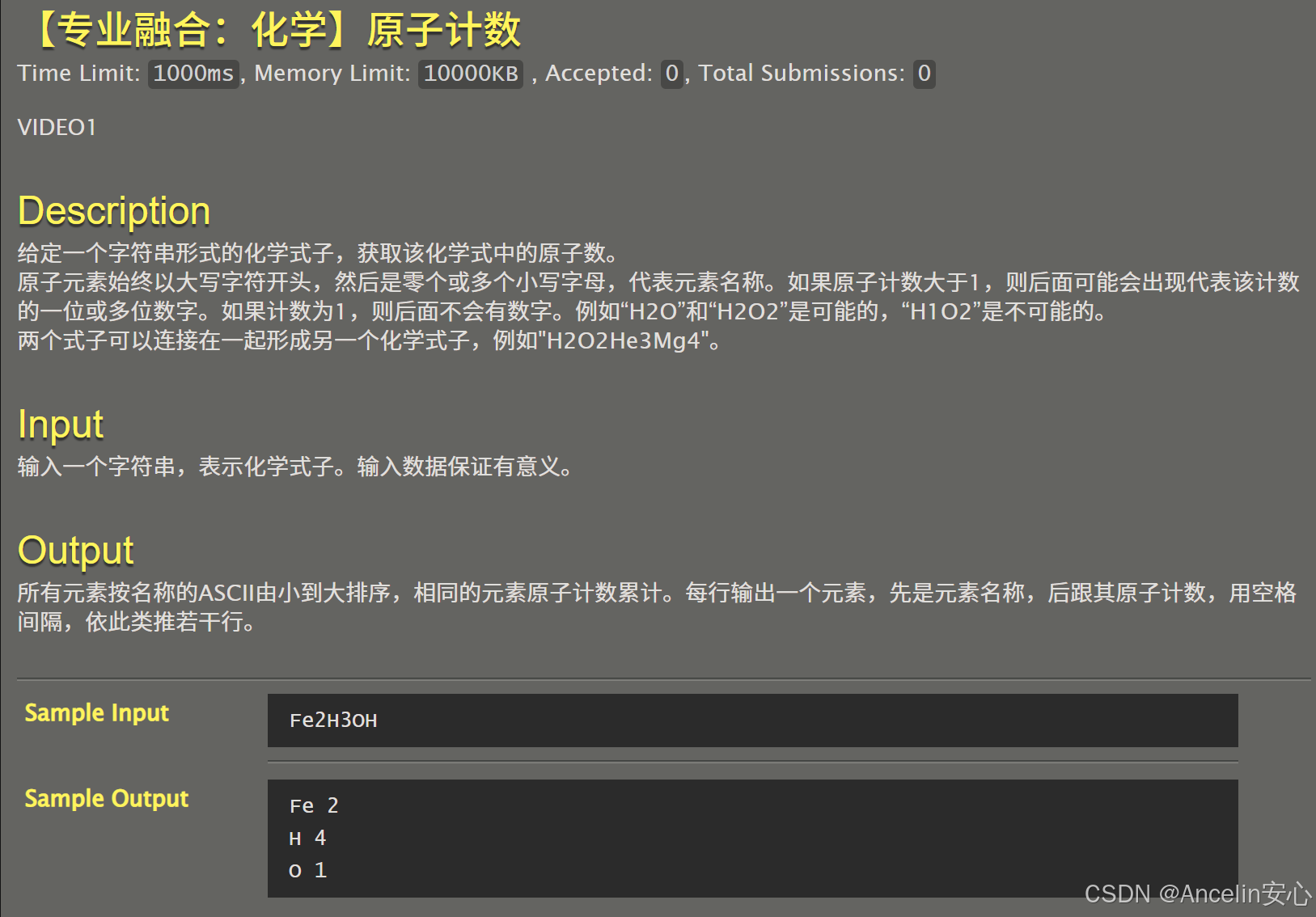
#include <bits/stdc++.h>
using namespace std;
struct Atom {
string name;
int count;
};
void resolve(string str,unordered_map<string,int>& atoms){
int i=0;
while(i<str.length()){
string atom_e="";
//检查首字母是否大写
if(isupper(str[i])){
atom_e+=str[i++];
}
//检查小写字母
while(i<str.length()&&islower(str[i])){
atom_e+=str[i++];
}
//读取元素数量
int count=0;
while(i<str.length()&&isdigit(str[i])){
count =count*10+(str[i++]-'0');
}
if(!count){
count=1;
}
atoms[atom_e]+=count;
}
}
int main() {
string str;
cin>>str;
unordered_map<string ,int> atoms;
resolve(str,atoms);
vector<Atom> elements;
for (const auto& entry : atoms) {
elements.push_back({entry.first, entry.second});
}
sort(elements.begin(), elements.end(), [](const Atom& a, const Atom& b) {
return a.name < b.name;
});
for (const auto& element : elements) {
cout << element.name << " " << element.count << endl;
}
}075:【专业融合:数学】中位数
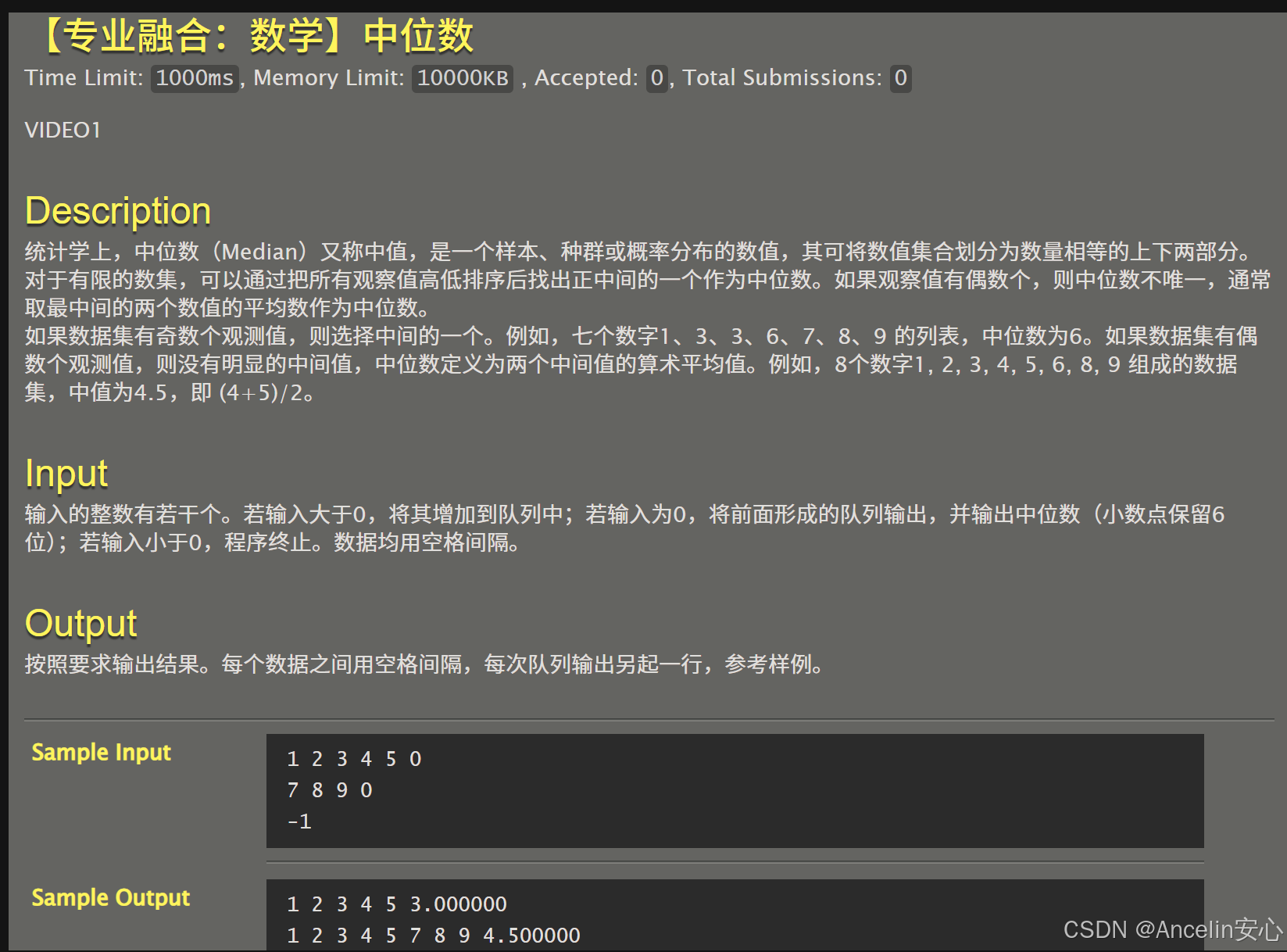
#include <stdio.h>
#include <stdlib.h>
int compare(const void *a, const void *b) {
return (*(int *)a - *(int *)b);
}
// 计算中位数
double calculateMedian(int *array, int size) {
// 将数组排序
qsort(array, size, sizeof(int), compare);
// 计算中位数
if (size % 2 == 1) {
return array[size / 2];
} else {
int middle1 = array[size / 2 - 1];
int middle2 = array[size / 2];
return (double)(middle1 + middle2) / 2;
}
}
int main() {
int input;
int *queue = NULL;
int size = 0;
while (1) {
scanf("%d", &input);
if (input > 0) {
size++;
queue = (int *)realloc(queue, size * sizeof(int));
queue[size - 1] = input;
}
else if (input == 0)
{
double median = calculateMedian(queue, size);
for (int i = 0; i < size; ++i) {
printf("%d ", queue[i]);
}
printf("%.6lf\n", median);
}
else if(input==-1)
{
break;
}
}
return 0;
}
076:【专业融合:力学】火箭发射模拟


#include <stdio.h>
int main() {
//火箭初始质量、火箭自身干质量、燃烧时间、有效排气速度cE、重力
double initialMass, dryMass, burnTime, exhaustVelocity, gravity;
scanf("%lf %lf %lf %lf %lf", &initialMass, &dryMass, &burnTime, &exhaustVelocity, &gravity);
// 推进剂质量
double propellantMass = initialMass - dryMass;
double time = 0.0;
double altitude = 0.0;
double velocity = 0.0;
// 时间步长
double timestep = 0.1;
double Mass_Flow=propellantMass/burnTime;
while (time <= burnTime) {
double thrust = Mass_Flow * exhaustVelocity;
// 加速度
double acceleration = (thrust / (dryMass + propellantMass)) ;
/*
//题目要求-g,但样例过不了
double acceleration = (thrust / (dryMass + propellantMass))-gravity;
*/
// 速度增量
double velocityIncrement = acceleration * timestep;
velocity += velocityIncrement;
// 海拔高度增量
double altitudeIncrement = velocity * timestep;
altitude += altitudeIncrement;
propellantMass -= Mass_Flow* timestep;
time += timestep;
}
printf("%.3lfkm\n", altitude/1000.0);
return 0;
}
077:成绩单

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
struct tagStudent{
char id[11];//学号
char name[31];//姓名
int score;//成绩
};
int compare(const void *a,const void *b){
int diff=((struct tagStudent*)b)->score - ((struct tagStudent*)a)->score;
if(diff==0){
return strcmp(((struct tagStudent *)a)->id, ((struct tagStudent *)b)->id);
}
return diff;
}
int main(){
int n;
scanf("%d",&n);
struct tagStudent students[n];
for(int i=0;i<n;i++){
scanf("%s %s %d", students[i].id, students[i].name, &students[i].score);
}
qsort(students,n,sizeof(struct tagStudent),compare);
for(int i=0;i<n;i++){
printf("%s %s %d\n", students[i].id, students[i].name, students[i].score);
}
}078:【专业融合:动能】热能计算


#include <stdio.h>
int main() {
double Ti, Tf;
scanf("%lf %lf", &Ti, &Tf);
double m_liquid, c_liquid;
scanf("%lf %lf", &m_liquid, &c_liquid);
double m_container, c_container;
scanf("%lf %lf", &m_container, &c_container);
double delta_T = Tf - Ti;
double Q = (m_liquid * c_liquid + m_container * c_container) * delta_T;
double percentage_container = (m_container * c_container * delta_T / Q) ;
double percentage_liquid = (m_liquid * c_liquid * delta_T / Q) ;
printf("%.2lfkJ,%.2lf%%,%.2lf%%\n", Q / 1000, percentage_container, percentage_liquid);
return 0;
}079:【专业融合:航天】卫星定位




#include <stdio.h>
#include <math.h>
#define N 11
#define c 299792.458
double X[N],A[N],B[N],C[N],T[N];
void scanf1(double A[N],int n){
for(int i=0;i<n;i++){
scanf("%lf",&A[i]);
}
}
void print1(double A[N],int n) { //输出一个矢量
int i,tmp;
double a;
for (i=0; i<n-1; i++){
tmp=(int)(A[i]*10000);
a=(double)tmp/10000.0;
printf("%.4lf,",a);
}
tmp=(int)(A[n-1]*10000);
a=(double)tmp/10000.0;
printf("%.4lf",a);
}
void print2(double A[N][N],int n) { //输出一个矩阵
int i, j;
for (i=0; i<n; i++) {
for (j=0; j<n; j++)
printf("%.7lf ", A[i][j]);
printf("\n");
}
}
// 计算代数余子式函数,结果=dest
int GetCoFactor(double dest[N][N], double src[N][N], int row, int col, int n)
{
int i, j;
int colCount=0,rowCount=0;
for(i=0; i<n; i++ ) {
if( i!=row ) {
colCount = 0;
for(j=0; j<n; j++ )
if( j != col ) { //当j不是元素时
dest[rowCount][colCount] = src[i][j];
colCount++;
}
rowCount++;
}
}
return 1;
}
// 递归计算行列式,结果=返回值
double CalcDeterminant(double mat[N][N], int n)
{
int i,j;
double det = 0; //行列式值
double minor[N][N]; // allocate 余子式矩阵
// n 必须 >= 0,当矩阵是单个元素时停止递归
if( n == 1 ) return mat[0][0];
for(i = 0; i < n; i++ ) {
GetCoFactor(minor, mat, 0, i , n);
det += ( i%2==1 ? -1.0 : 1.0 ) * mat[0][i] * CalcDeterminant(minor,n-1);
}
return det;
}
// 伴随矩阵法矩阵求逆 , 结果存放到 inv 数组
void MatrixInversion(double J[N][N], int n)
{
int i,j;
double det, temp [N][N], minor[N][N];
double inv[N][N];
det = 1.0/CalcDeterminant(J,n); //计算行列式
for(j=0; j<n; j++)
for(i=0; i<n; i++) {
// 得到矩阵A(j,i)的代数余子式
GetCoFactor(minor,J,j,i,n);
inv[i][j] = det*CalcDeterminant(minor,n-1);
if( (i+j)%2 == 1)
inv[i][j] = -inv[i][j];
}
//结果存回J矩阵
for(j=0; j<n; j++)
for(i=0; i<n; i++)
J[i][j] = inv[i][j];
}
// 由Xn计算函数Fn,结果存放到 F
void CalcF(double F[N],double X[N],int n) {
double f;
int i;
for (i=0; i<n; i++) {
switch (i+1) {
case 1:
f=X[0]*X[0]+X[1]*X[1]-2*X[0]-X[2]+1; //x^2+y^2-2x-z+1
break;
case 2:
f=X[0]*X[1]*X[1]-X[0]-3*X[1]+X[1]*X[2]+2; //xy^2-x-3y+yz+2
break;
case 3:
f=X[0]*X[2]*X[2]-3*X[2]+X[1]*X[2]*X[2]+X[0]*X[1]; //xz^2-3z+yz^2+xy
break;
}
F[i]=f;
}
}
void CalcF_re(double F[N],double X[N],int n) {
double f;
int i;
for (i=0; i<n; i++) {
switch (i+1) {
case 1:
f=(X[0]-A[0])*(X[0]-A[0])+(X[1]-B[0])*(X[1]-B[0])+(X[2]-C[0])*(X[2]-C[0])-(c*(T[0]-X[3]))*(c*(T[0]-X[3]));
break;
case 2:
f=(X[0]-A[1])*(X[0]-A[1])+(X[1]-B[1])*(X[1]-B[1])+(X[2]-C[1])*(X[2]-C[1])-(c*(T[1]-X[3]))*(c*(T[1]-X[3]));
break;
case 3:
f=(X[0]-A[2])*(X[0]-A[2])+(X[1]-B[2])*(X[1]-B[2])+(X[2]-C[2])*(X[2]-C[2])-(c*(T[2]-X[3]))*(c*(T[2]-X[3]));
break;
case 4:
f=(X[0]-A[3])*(X[0]-A[3])+(X[1]-B[3])*(X[1]-B[3])+(X[2]-C[3])*(X[2]-C[3])-(c*(T[3]-X[3]))*(c*(T[3]-X[3]));
}
F[i]=f;
}
}
// 由Xn计算偏导数Jacobian矩阵F'n,结果存放到 J
void CalcJ(double J[N][N],double X[N],int n) {
double f;
int i,j;
for (i=0; i<n; i++)
switch (i+1) {
case 1:
for (j=0; j<n; j++) {
switch (j+1) {
case 1: f=2*X[0]-2;break; // J1.1=2x-2
case 2: f=2*X[1];break; // J1.2=2y
case 3: f=-1;break; // J1.3=-1
}
J[i][j]=f;
}
break;
case 2:
for (j=0; j<n; j++) {
switch (j+1) {
case 1: f=X[1]*X[1]-1;break; // J2.1=y^2-1
case 2: f=2*X[0]*X[1]-3+X[2];break; // J2.2=2xy-3+z
case 3: f=X[1];break; // J2.3=y
}
J[i][j]=f;
}
break;
case 3:
for (j=0; j<n; j++) {
switch (j+1) {
case 1: f=X[2]*X[2]+X[1];break; // J3.1=z^2+y
case 2: f=X[2]*X[2]+X[0];break; // J3.2=z^2+x
case 3: f=2*X[0]*X[2]-3+2*X[1]*X[2];break; // J3.3=2xz-3+2yz
}
J[i][j]=f;
}
break;
}
}
// 由Xn计算偏导数Jacobian矩阵F'n,结果存放到 J
void CalcJ_re(double J[N][N],double X[N],int n) {
double f;
int i,j;
for (i=0; i<n; i++)
switch (i+1) {
case 1:
for (j=0; j<n; j++) {
switch (j+1) {
case 1: f=2*(X[0]-A[0]);break; // J1.1=2(x-A1)
case 2: f=2*(X[1]-B[0]);break; // J1.2=2(y-B1)
case 3: f=2*(X[2]-C[0]);break; // J1.3=2(z-C1)
case 4: f=2*c*c*(T[0]-X[3]);break;//J1.4=2*c^2(t1-d)
}
J[i][j]=f;
}
break;
case 2:
for (j=0; j<n; j++) {
switch (j+1) {
case 1: f=2*(X[0]-A[1]);break; // J1.1=2(x-A1)
case 2: f=2*(X[1]-B[1]);break; // J1.2=2(y-B1)
case 3: f=2*(X[2]-C[1]);break; // J1.3=2(z-C1)
case 4: f=2*c*c*(T[1]-X[3]);break;//J1.4=2*c^2(t1-d)
}
J[i][j]=f;
}
break;
case 3:
for (j=0; j<n; j++) {
switch (j+1) {
case 1: f=2*(X[0]-A[2]);break; // J1.1=2(x-A1)
case 2: f=2*(X[1]-B[2]);break; // J1.2=2(y-B1)
case 3: f=2*(X[2]-C[2]);break; // J1.3=2(z-C1)
case 4: f=2*c*c*(T[2]-X[3]);break;//J1.4=2*c^2(t1-d)
}
J[i][j]=f;
}
break;
case 4:
for (j=0; j<n; j++) {
switch (j+1) {
case 1: f=2*(X[0]-A[3]);break; // J1.1=2(x-A1)
case 2: f=2*(X[1]-B[3]);break; // J1.2=2(y-B1)
case 3: f=2*(X[2]-C[3]);break; // J1.3=2(z-C1)
case 4: f=2*c*c*(T[3]-X[3]);break;//J1.4=2*c^2(t1-d)
}
J[i][j]=f;
}
break;
}
}
// 计算 J^-1* F,结果存放到 R
void CalcJF(double R[N], double J[N][N], double F[N], int n) {
int i,j,k;
for (i=0; i<n; i++) {
R[i]=0.0;
for (j=0; j<n; j++)
R[i] = R[i] + J[i][j]*F[j];
}
}
// 计算 X=X0-R,结果存放到 X
void CalcX(double X[N],double X0[N],double R[N],int n) {
int i;
for (i=0; i<n; i++)
X[i]=X0[i]-R[i];
}
// 计算 A=B,结果存放到 A
void AequB(double A[N],double B[N],int n) {
int i;
for (i=0; i<n; i++)
A[i]=B[i];
}
// 计算 F-
double Ferror(double F[N], int n) {
double m=0;
int i;
for (i=0; i<n; i++) {
double t=fabs(F[i]);
if (m<t) m = t;
}
return m;
}
// Newton–Raphson method 牛顿迭代法求非线性方程组的根,存放到X0
void mvNewtons(double X0[N], int n, double e) {
// Guess为初始猜测值 e为迭代精度要求
int k;
double J[N][N],Y[N][N];
double X[N],R[N],F[N];
//X0一开始为初始猜测值
for (k=1; k<=20; k++) { //限定20次迭代
/*
printf("-------------- n=%d\n",k);
printf("X\n");
print1(X0,n); //输出X0
*/
CalcF_re(F,X0,n); //计算F矩阵
/*
printf("F\n"); //观察 F
print1(F,n); //输出F
*/
CalcJ_re(J,X0,n); //计算Jacobian矩阵F'n(x0)
/*
printf("J\n");
print2(J,n); //观察 J
*/
MatrixInversion(J, n); // 求J的逆矩阵 J^-1
CalcJF(R,J,F,n); // R=J^-1 * F
CalcX(X,X0,R,n); // X=X0-R
AequB(X0,X,n); // X0=X 下次迭代
if (Ferror(F,n)<e) break; //达到精度要求,终止迭代
}
}
int main() {
int n=4;
scanf("%lf %lf %lf",&A[0],&B[0],&C[0]);
scanf("%lf %lf %lf",&A[1],&B[1],&C[1]);
scanf("%lf %lf %lf",&A[2],&B[2],&C[2]);
scanf("%lf %lf %lf",&A[3],&B[3],&C[3]);
scanf1(T,n);
scanf1(X,n);
mvNewtons(X,n,1e-6); //根存放在X
print1(X,3);
return 0;
}
080:【专业融合:天文】日出日落时间


 题干链接无法正常访问,可参考:Solar Calculator - NOAA Global Monitoring Laboratory
题干链接无法正常访问,可参考:Solar Calculator - NOAA Global Monitoring Laboratory
题解1:(WA,原因是无法正常访问题干链接)
#include <cmath>
#include <iostream>
#include <iomanip>
#define M_PI 3.14159265358979323846
using namespace std;
double degToRad(double deg) {
return deg * M_PI / 180.0;
}
double calcSolarDeclination(int dayOfYear) {
return 0.4093 * sin((2.0 * M_PI / 365.0) * dayOfYear - 1.405);
}
double calcTime(int year, int month, int day, double longitude, double latitude, bool sunrise, int timezone) {
int dayOfYear = (month - 1) * 30 + day;
double declination = calcSolarDeclination(dayOfYear);
double time = 12.0 + (sunrise ? -1 : 1) * acos(( sin(degToRad(-0.83)) - sin(degToRad(latitude)) * sin(declination)) / ( cos(degToRad(latitude)) * cos(declination))) / M_PI * 180.0 / 15.0;
return time - 4.0 * longitude / 60.0 + timezone;
}
int main() {
int year, month, day, timezone;
double longitude, latitude;
cin >> year >> month >> day ;
cin >> longitude >> latitude ;
cin >> timezone;
double sunrise = calcTime(year, month, day, longitude, latitude, true, timezone);
double sunset = calcTime(year, month, day, longitude, latitude, false, timezone);
double noon = calcTime(year, month, day, longitude, latitude, false, timezone) - (sunset - sunrise) / 2;
cout <<"Solar Noon="<< setfill('0') << setw(2) << int(noon) << ":" << setw(2) << int((noon - int(noon)) * 60) << ":" << setw(2) << int(((noon - int(noon)) * 60 - int((noon - int(noon)) * 60)) * 60) << endl;
cout <<" Sunrise="<< setfill('0') << setw(2) << int(sunrise) << ":" << setw(2) << int((sunrise - int(sunrise)) * 60) << ":" << setw(2) << int(((sunrise - int(sunrise)) * 60 - int((sunrise - int(sunrise)) * 60)) * 60) << endl;
cout <<" Sunset="<< setfill('0') << setw(2) << int(sunset) << ":" << setw(2) << int((sunset - int(sunset)) * 60) << ":" << setw(2) << int(((sunset - int(sunset)) * 60 - int((sunset - int(sunset)) * 60)) * 60) << endl;
return 0;
}题解2:作者尝试根据新链接重新写的,尚未测试
#include <cmath>
#include <iostream>
#include <iomanip>
#define M_PI 3.14159265358979323846
using namespace std;
double degToRad(double deg) {
return deg * M_PI / 180.0;
}
double radToDeg(double rad) {
return rad * 180.0 / M_PI;
}
// Calculate the day of the year
int calcDayOfYear(int year, int month, int day) {
int daysInMonth[] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
if ((year % 4 == 0 && year % 100 != 0) || year % 400 == 0) {
daysInMonth[1] = 29; // Leap year
}
int dayOfYear = 0;
for (int i = 0; i < month - 1; ++i) {
dayOfYear += daysInMonth[i];
}
dayOfYear += day;
return dayOfYear;
}
// Calculate the solar declination
double calcSolarDeclination(double dayOfYear) {
return 23.44 * sin(degToRad(360.0 / 365.0 * (dayOfYear - 81)));
}
// Calculate the equation of time
double calcEquationOfTime(double dayOfYear) {
double B = degToRad(360.0 / 365.0 * (dayOfYear - 81));
return 9.87 * sin(2 * B) - 7.53 * cos(B) - 1.5 * sin(B);
}
// Calculate the hour angle
double calcHourAngle(double latitude, double declination, bool isSunrise) {
double latRad = degToRad(latitude);
double declRad = degToRad(declination);
double cosH = (cos(degToRad(90.833)) / (cos(latRad) * cos(declRad)) - tan(latRad) * tan(declRad));
if (cosH > 1.0 || cosH < -1.0) {
return NAN; // Sun never rises or sets
}
double hourAngle = radToDeg(acos(cosH));
return isSunrise ? -hourAngle : hourAngle;
}
// Calculate solar time
double calcSolarTime(double longitude, double standardMeridian, double equationOfTime) {
return 4.0 * (longitude - standardMeridian) + equationOfTime;
}
// Format time as HH:MM:SS
string formatTime(double timeInHours) {
if (isnan(timeInHours)) return "N/A";
int hours = int(timeInHours);
int minutes = int((timeInHours - hours) * 60);
int seconds = int(((timeInHours - hours) * 60 - minutes) * 60);
char buffer[9];
snprintf(buffer, sizeof(buffer), "%02d:%02d:%02d", hours, minutes, seconds);
return string(buffer);
}
int main() {
int year, month, day;
double longitude, latitude, timezone;
cin >> year >> month >> day;
cin >> longitude >> latitude;
cin >> timezone;
int dayOfYear = calcDayOfYear(year, month, day);
double declination = calcSolarDeclination(dayOfYear);
double equationOfTime = calcEquationOfTime(dayOfYear);
double standardMeridian = timezone * 15.0;
double solarNoon = 12.0 - calcSolarTime(longitude, standardMeridian, equationOfTime) / 60.0;
double hourAngleSunrise = calcHourAngle(latitude, declination, true);
double hourAngleSunset = calcHourAngle(latitude, declination, false);
double sunrise = solarNoon + hourAngleSunrise / 15.0;
double sunset = solarNoon + hourAngleSunset / 15.0;
cout << right;
cout << "Solar Noon=" << formatTime(solarNoon) << endl;
cout << " Sunrise=" << formatTime(sunrise) << endl;
cout << " Sunset=" << formatTime(sunset) << endl;
return 0;
}
081:【算法策略:回溯】 游乐园(dfs)


#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int n,m;
int map[1000][1000]={0};
int used[1000]={0};
int MAX=0;;
int max(int x, int y){
if(x>y) return x;
return y;
}
void dfs(int s,int sum){
MAX=max(MAX,sum);
for(int i=1;i<=n;i++){
if(map[s][i]&&!used[i]){
used[i]=1;
dfs(i,sum+map[s][i]);
used[i]=0;
}
}
}
int main(){
scanf("%d %d",&n,&m);
int a,b,c;
memset(map,0,sizeof(map));
for(int i=0;i<m;i++){
scanf("%d %d %d",&a,&b,&c);
map[a][b]=c;
map[b][a]=c;
}
for(int i=1;i<=n;i++){
memset(used,0,sizeof(used));
used[i]=1;
dfs(i,0);
}
printf("%d\n",MAX);
}
082:【算法策略:动态规划】上楼梯

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int solve(int N,int M,int *bad){
int dp[N+1];
memset(dp,0,sizeof(dp));
for(int i=0;i<M;i++){
dp[bad[i]]=-1;
}
dp[0]=1;
if(dp[1]!=-1)dp[1]=1;
else dp[1]=0;
for(int i=2;i<=N;i++){
if(dp[i]==-1){
dp[i]=0;
}
else{
dp[i]=(dp[i-1]+dp[i-2])%1000000007;
}
}
return dp[N];
}
int main(){
int N,M;
scanf("%d %d",&N,&M);
int *bad=(int *)malloc(M*sizeof(int));
for(int i=0;i<M;i++){
scanf("%d",&bad[i]);
}
printf("%d\n",solve(N,M,bad));
}
083:【算法策略:动态规划】挑选

#include <stdio.h>
#include <time.h>
#include <limits.h>
#include <stdlib.h>
int max(int a, int b) {
return (a > b) ? a : b;
}
void quickSort(long long arr[], long long left, long long right) {
if (left >= right) return;
srand(time(NULL));
long long idx = rand() % (left - right) + left;
long long flag = arr[idx], head = left - 1, tail = right + 1;
while (head < tail) {
do head++; while(arr[head] < flag);
do tail--; while(arr[tail] > flag);
if (head < tail) {
long long tmp = arr[head];
arr[head] = arr[tail];
arr[tail] = tmp;
}
}
quickSort(arr, left, tail);
quickSort(arr, tail + 1, right);
}
int main() {
long long n;
scanf("%lld", &n);
long long arr[n];
// 输入序列
for (int i = 0; i < n; i++) {
scanf("%lld", &arr[i]);
}
quickSort(arr,0,n-1);
// 初始化动态规划数组
int dp[n];
dp[0] = arr[0];
int MAX=0;
// 动态规划递推
for (int i = 1; i < n; i++) {
/*
当arr[i]和前一个数字相等时,判断正负数,即相加后是否变小即可,选大的填入
*/
if(arr[i]==arr[i-1])
{
dp[i]=max(dp[i-1],dp[i-1]+arr[i]);
}
/*
存在111112333334555555这种情况
*/
else{
int j=i-1;
while(j>=0&&arr[j]==arr[i]-1) j--;
if(j>=0){
dp[i]=arr[i]+dp[j];
}
else
{
dp[i]=arr[i];
}
}
MAX=max(MAX,dp[i]);
}
printf("%d\n", MAX);
return 0;
}
084:【算法策略:分治】子数组最大和

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int main(){
int n;
scanf("%d",&n);
int a[n];
int dp[n];
for(int i=0; i<n; i++){
scanf("%d",&a[i]);
dp[i]=a[i];
}
for(int i=1;i<n;i++){
if(dp[i]+dp[i-1]>dp[i]){
dp[i]=dp[i]+dp[i-1];
}
}
int max=0;
for(int i=0;i<n;i++){
if(dp[i]>max) max=dp[i];
}
printf("%d\n",max);
}
085:【算法策略:贪心】绝对差

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
int partition(int arr[], int low, int high) {
int pivot = arr[high];
int i = low - 1;
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return i + 1;
}
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pivotIndex = partition(arr, low, high);
quickSort(arr, low, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, high);
}
}
int main(){
int n;
scanf("%d",&n);
int arr[n];
for(int i=0; i<n; i++){
scanf("%d",&arr[i]);
}
quickSort(arr,0,n-1);
int min=9999999;
for(int i=0;i<n-1;i++){
if(abs(arr[i+1]-arr[i])<min){
min=abs(arr[i+1]-arr[i]);
}
}
printf("%d\n",min);
}
086:【算法策略:贪心】三角形

快排模板:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
//快排模板
void quicksort(int arr[], int l, int r)
{
if (l >= r)
{
return;
}
else
{
int i = l - 1;
int j = r + 1;
int x = arr[(l + r) / 2];
while (i < j)
{
do
{
i++;
} while (arr[i] > x);
do
{
j--;
} while (arr[j] < x);
if (i < j)
{
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
quicksort(arr, l, j);
quicksort(arr, j + 1, r);
}
}
void is_Triangle(int arr[], int n){
for(int i=0;i<n-2;i++){
if(arr[i]<arr[i+1]+arr[i+2]){
printf("%d %d %d\n",arr[i+2],arr[i+1],arr[i]);
return ;
}
}
printf("-1");
}
int main(){
int n;
scanf("%d", &n);
int a[n];
for(int i=0;i<n;i++){
scanf("%d", &a[i]);
}
quicksort(a,0,n-1);
is_Triangle(a,n);
}
087:【算法策略:动态规划】打字机

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_LEN 1000
int main() {
char str[MAX_LEN];
scanf("%s", str);
int len = strlen(str);
for (int i = 0; i < len; ++i) {
if (str[i] == 'm' || str[i] == 'w') {
printf("0\n");
return 0;
}
}
long long dp[MAX_LEN];
dp[0] = 1;
dp[1] = 1;
for (int i = 1; i < len; ++i) {
dp[i + 1] = dp[i];
if ((str[i] == 'n' && str[i - 1] == 'n') || (str[i] == 'u' && str[i - 1] == 'u')) {
dp[i + 1] += dp[i - 1];
}
}
printf("%lld\n", dp[len]);
return 0;
}
088:【算法策略:贪心】汤包

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
struct customer{
int t;
int d;
int etime;
int index;
};
int main(){
int n;
scanf("%d",&n);
struct customer a[n];
for(int i=0; i<n; i++){
a[i].index=i+1;
scanf("%d %d",&a[i].t,&a[i].d);
a[i].etime=a[i].t+a[i].d;
}
for(int i=0;i<n-1;i++){
for(int j=0;j<n-1-i;j++){
if((a[j].etime>a[j+1].etime)||((a[j].etime==a[j+1].etime)&&a[j].index>a[j+1].index)){
int tmp=a[j].etime;
a[j].etime=a[j+1].etime;
a[j+1].etime=tmp;
tmp=a[j].index;
a[j].index=a[j+1].index;
a[j+1].index=tmp;
}
}
}
for(int i=0;i<n;i++){
printf("%d ",a[i].index);
}
}
089:【算法策略:优雅的策略】危险的组合(递推、动态规划、打表)

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int n;
int num;
int a[30];
void dfs(int i,int flag){
if(i==n) {
if(flag>=1) num++;
return;
}
for(int j=0;j<2;j++){
a[i]=j;
if(i>=2&&a[i-1]==a[i]&&a[i-1]==a[i-2]&&a[i]==1){
dfs(i+1,flag+1);
}
else{
dfs(i+1,flag);
}
}
}
int main(){
while(1){
scanf("%d",&n);
num=0;
if(n<=0) break;
dfs(0,0);
printf("%d\n",num);
}
}
090:【塞纳策略:回溯】和字符串

#include <stdio.h>
#include <string.h>
#include <stdbool.h>
long long substrToNum(char str[], int pos, int len) {
long long num = 0;
for (int i = 0; i < len; ++i)
num = num * 10 + str[pos + i] - '0';
return num;
}
long long getLen(long long n) {
int cnt = 0;
do ++cnt, n /= 10; while(n);
return cnt;
}
bool backTracking(char str[], int strLen, int begin, int len1, int len2) {
if (begin + len1 + len2 >= strLen) return true;
long long num1 = substrToNum(str, begin, len1);
long long num2 = substrToNum(str, begin + len1, len2);
long long num3 = substrToNum(str, begin + len1 + len2, getLen(num1 + num2));
printf("%lld,%lld,%lld\n", num1, num2, num3);
if (num1 + num2 == num3) return backTracking(str, strLen, begin + getLen(num1), getLen(num2), getLen(num3));
return false;
}
void partition(char str[]) {
int strLen = strlen(str);
for (int i = 1; i <= strLen / 2; ++i) {
if (backTracking (str, strLen, 0, i, i)) {
printf("true\n");
return;
}
}
printf("false\n");
}
int main() {
char str[1000] = "";
scanf("%s", str);
partition(str);
return 0;
}
091 【考试题型(循环/迭代)】:圆周率π
重点考察条件型和计数型循环,注意计数控制,初值设置,正负交替,两数交换等小技巧。

读题只读关键

把它抽象成数学公式即可,作为关键代码行
#include<stdio.h>
int main(){
int n,t=1;
double result=3.0,d=2.0;
scanf("%d", &n);
for(int i=1;i<n;i++){
result+=t*4/(d*(d+1)*(d+2));
d+=2;
t=-t;
}
printf("%.7lf", result);
}
092:【考试题型:条件分支】马赫数


考试时如果题目没有明确给出区间的开闭情况,或者题目有任何模糊不清的地方,一定及时跟监考老师反馈。
#include<stdio.h>
#include<math.h>
int main(){
double v,c,T,M;
scanf("%lf", &v);
scanf("%lf", &T);
c = 331.3*sqrt(1.0+T/273.15);
v = v/3.6;
M = v/c;
if(M<=0.8)printf("%.3lf subsonic", M);
else if(M<=1.2)printf("%.3lf transonic", M);
else if(M<=5.0)printf("%.3lf supersonic", M);
else printf("%.3lf hypersonic", M);
return 0;
}
093:【考试题型:文件】平方根

文件题有开就有闭,很像操作系统里的PV操作,总是成对出现。
#include <stdio.h>
#include <math.h>
int main(){
FILE *fp;
int n,i;
double x;
scanf("%d", &n);
fp = fopen("rr.dat", "w");
for(i=1;i<=n;i++){
fprintf(fp,"%.6lf\n",sqrt((double)i));
}
fclose(fp);
fp=fopen("rr.dat", "r");
for(i=1;i<=n;i++){
fscanf(fp,"%lf",&x);
printf("%lf ",x);
}
fclose(fp);
return 0;
}
注意fprintf()那行代码,我们之前用的printf其实在fp的位置省略了参数screen,意思是把参数的值打印到屏幕上,这里fp是指把参数的值打印到fp指针指向的rr.dat文件里。
094:【考试题型:结构体】空中交通管制


结构体也非常简单,是送分题,读者如果学习C++或者java这类面向对象的编程语言都会学习到类的概念,就很类似C语言中的结构体。
//【考试题型:结构体】空中交通管制
#include <stdio.h>
#include <math.h>
typedef struct tagFlight { //重点考查 结构体及自定义数据类型
char id[7];
double x, y;
} Flight; //不用结构体肯定要吃苦头
double dist(Flight a, Flight b) {
return sqrt((a.x - b.x)*(a.x - b.x) +
(a.y - b.y)*(a.y - b.y));
}
int main() {
Flight a[1000]; //雷达屏上有1000架飞机,和平时期不可能
int n, i, j, d_i, d_j;
double mind, d;
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%s%lf%lf", &a[i].id, &a[i].x, &a[i].y);
mind = 4000000; //这距离是月球和地球的
for (i = 0; i < n; i++)
for (j = i + 1; j < n; ++j) { //枚举算法
d = dist(a[i], a[j]);
if (d < mind) mind = d, d_i = i, d_j = j; //新的最小距离
}
printf("%s-%s %.4lf", a[d_i].id, a[d_j].id, mind);
return 0;
}
代码我们只要积累使用枚举算法寻找最短距离的方法即可,同时更新最小距离这一句也很巧妙,省去了排序这一步。
095:【考试题型:算法策略】零钞
这道题可以利用贪心算法,先找零10元,然后5元,2元,1元;实际上1元最多只能找一张,因为一旦找了两张1元就可以换成找一张2元了。(此题难度堪比前10题)
题解1:
#include <stdio.h>
#include <math.h>
int main() {
int n;
scanf("%d", &n);
int num2=0,num5=0,num10=0;
while(n>=10){
n-=10;
num10++;
}
while(n>=5){
n-=5;
num5++;
}
while(n>=2){
n-=2;
num2++;
}
if(n==1)printf("1=1\n");
if(num2)printf("2=%d\n", num2);
if(num5)printf("5=%d\n", num5);
if(num10)printf("10=%d\n", num10);
return 0;
}
题解2:

096:【考试题型:输入输出】气体扩散


#include <stdio.h>
#include <math.h>
int main() {
double a,b,rate;
scanf("%lf %lf", &a, &b);
rate=sqrt(b/a);
printf("%.4lf", rate);
return 0;
}
097:【考试题型:函数(递归)】阿克曼函数

#include <stdio.h>
#include <math.h>
int Ack(int m, int n){
if(m==0)return n+1;
if(n==0)return Ack(m-1,1);
else return Ack(m-1,Ack(m,n-1));
}
int main() {
int m,n;
scanf("%d %d", &m, &n);
int a=Ack(m,n);
printf("%d", a);
return 0;
}
这里注意m和m-1的关系,代码不能完全照抄题目公式。
098:【考试题型:数组】重复元素

099:【考试题型:枚举】机场翻牌显示

题解1:
题解2: (代码中有部分库是用不到的,读者可以当做练习判断哪些库是不必要的)
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
int main(){
char str1[10];
char str2[10];
int sum=0;
scanf("%s",str1);
scanf("%s",str2);
for(int i=0;i<6;i++){
if(i<=1){
sum+=(str2[i]-str1[i]+26)%26;
}
else {
sum+=(str2[i]-str1[i]+10)%10;
}
}
printf("%d\n",sum);
}
100:【考试题型:字符串】左右操作
题解1:


‘&’为按位与操作,n&00000000..1,由于n的高n-1位与0于后都为0,只看最低位为1,n是奇数,n&1=1; n是偶·数,n&1=0。
题解2:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
//快排模板
void quicksort(char arr[], int l, int r)
{
if (l >= r)
{
return;
}
else
{
int i = l - 1;
int j = r + 1;
char x = arr[(l + r) / 2];
while (i < j)
{
do
{
i++;
} while (arr[i] > x);
do
{
j--;
} while (arr[j] < x);
if (i < j)
{
char tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
quicksort(arr, l, j);
quicksort(arr, j + 1, r);
}
}
void swap(char arr[],int l,int r){
for(int i=l;i<(r-l+1)/2+l;i++){
char tmp=arr[i];
int x=r-1-(i-l);
arr[i]=arr[x];
arr[x]=tmp;
}
}
int main(){
char str[1000];
scanf("%s", str);
int n=strlen(str);
quicksort(str, 0,n/2-1);
int right_s=n%2?n/2+1:n/2;
swap(str,right_s,n);
printf("%s\n",str);
}

恭喜你坚持到了最后,noj100题已全部攻克!










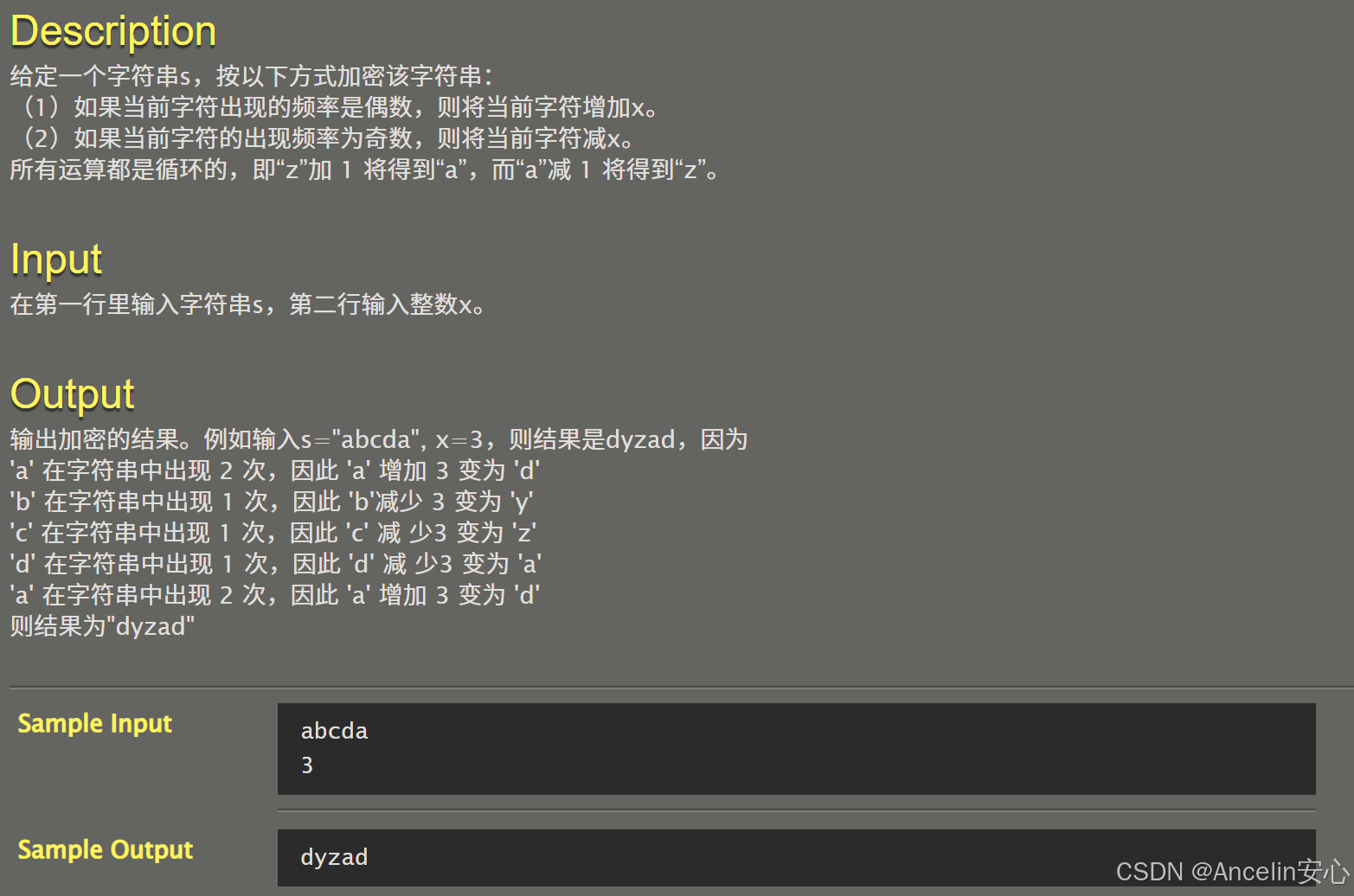

















 1995
1995

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








