LeetCode题练习与总结：天际线问题--218

一、题目描述

城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度，请返回 由这些建筑物形成的 天际线 。

每个建筑物的几何信息由数组 buildings 表示，其中三元组 buildings[i] = [lefti, righti, heighti] 表示：

• lefti 是第 i 座建筑物左边缘的 x 坐标。
• righti 是第 i 座建筑物右边缘的 x 坐标。
• heighti 是第 i 座建筑物的高度。

你可以假设所有的建筑都是完美的长方形，在高度为 0 的绝对平坦的表面上。

天际线 应该表示为由 “关键点” 组成的列表，格式 [[x1,y1],[x2,y2],...] ，并按 x 坐标 进行 排序 。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点，y 坐标始终为 0 ，仅用于标记天际线的终点。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

注意：输出天际线中不得有连续的相同高度的水平线。例如 [...[2 3], [4 5], [7 5], [11 5], [12 7]...] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[...[2 3], [4 5], [12 7], ...]

示例 1：

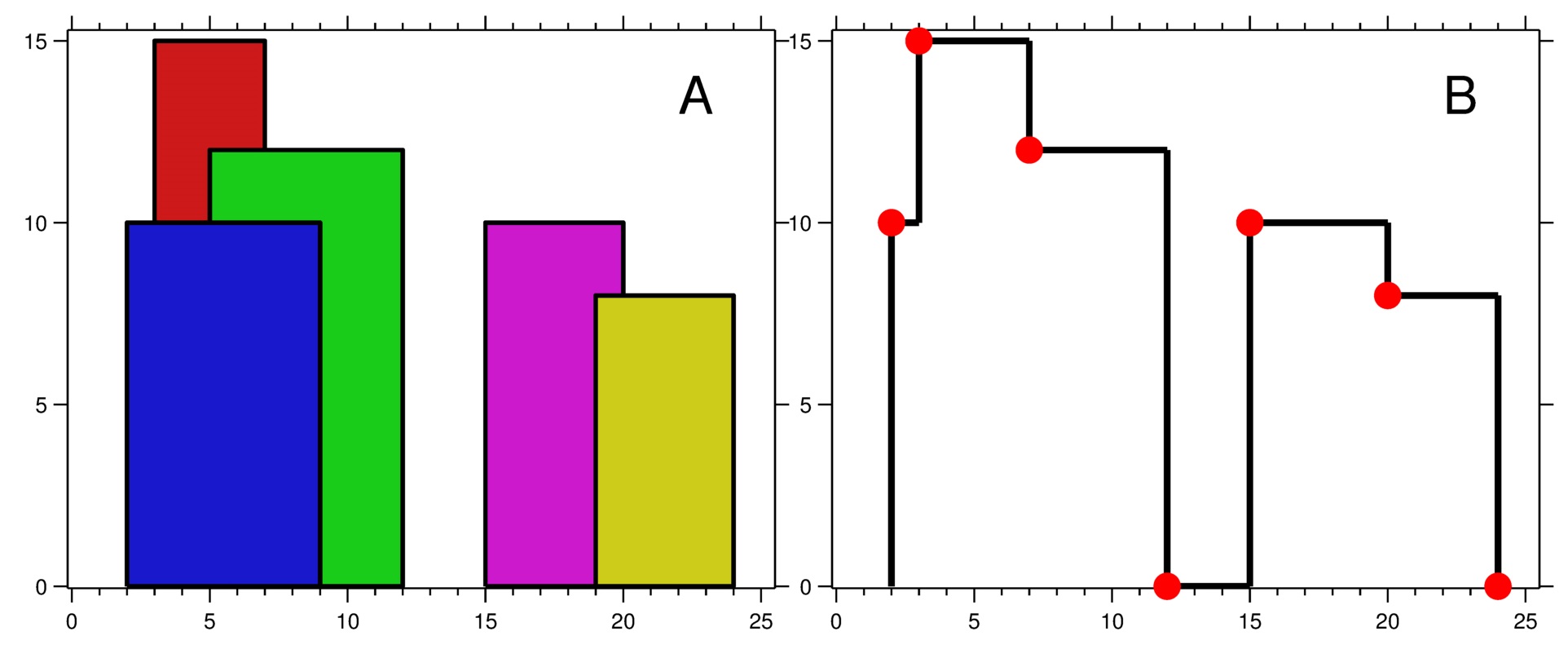
输入：buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
输出：[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释：
图 A 显示输入的所有建筑物的位置和高度，
图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。

示例 2：

输入：buildings = [[0,2,3],[2,5,3]]
输出：[[0,3],[5,0]]

提示：

• 1 <= buildings.length <= 10^4
• 0 <= lefti < righti <= 2^31 - 1
• 1 <= heighti <= 2^31 - 1
• buildings 按 lefti 非递减排序

二、解题思路

1. 首先，我们需要将所有建筑物的左边缘和右边缘加入到一个列表中，并按照x坐标进行排序。同时，左边缘的高度为负数，右边缘的高度为正数，这样可以在排序后区分左右边缘。

2. 然后，我们需要使用一个优先队列（最大堆）来维护当前所有建筑物的高度。优先队列中存储的是负数的高度，这样我们可以确保队列的队首始终是当前最高的建筑物。

3. 遍历排序后的边缘列表，每次遇到左边缘时，将对应的高度加入优先队列；遇到右边缘时，从优先队列中移除对应的高度。

4. 在处理每个边缘时，如果当前边缘的x坐标与前一个关键点的x坐标不同，则比较当前优先队列的队首元素（即当前最高建筑物的高度）与上一个关键点的高度。如果不同，则将当前边缘的x坐标和高度（取绝对值）作为一个新的关键点加入结果列表。

5. 最后，返回结果列表。

三、具体代码

import java.util.*;

class Solution {
    public List<List<Integer>> getSkyline(int[][] buildings) {
        // 存储所有边缘的列表
        List<int[]> edges = new ArrayList<>();
        
        // 将所有建筑物的左边缘和右边缘加入列表
        for (int[] building : buildings) {
            edges.add(new int[]{building[0], -building[2]});
            edges.add(new int[]{building[1], building[2]});
        }
        
        // 按照x坐标进行排序，如果x坐标相同，则按照高度进行排序
        Collections.sort(edges, (a, b) -> {
            if (a[0] != b[0]) {
                return a[0] - b[0];
            } else {
                return a[1] - b[1];
            }
        });
        
        // 优先队列，存储当前所有建筑物的高度（存储负数，以实现最大堆的效果）
        PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> b - a);
        pq.offer(0); // 初始化优先队列，加入地面高度
        
        // 结果列表
        List<List<Integer>> res = new ArrayList<>();
        
        // 上一个关键点的高度
        int prevHeight = 0;
        
        // 遍历所有边缘
        for (int[] edge : edges) {
            int x = edge[0];
            int height = edge[1];
            
            // 如果是左边缘，加入优先队列
            if (height < 0) {
                pq.offer(-height);
            } else { // 如果是右边缘，从优先队列中移除
                pq.remove(height);
            }
            
            // 获取当前最高建筑物的高度
            int curHeight = pq.peek();
            
            // 如果当前边缘的x坐标与前一个关键点的x坐标不同，或者高度发生变化
            if (prevHeight != curHeight) {
                res.add(Arrays.asList(x, curHeight));
                prevHeight = curHeight;
            }
        }
        
        return res;
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

• 首先，我们将所有建筑物的左边缘和右边缘加入到一个列表中。这个步骤需要遍历所有建筑物，每个建筑物需要常数时间操作，所以这一步的时间复杂度是 O(n)，其中 n 是建筑物的数量。

• 然后，我们对这个列表进行排序。排序操作的时间复杂度是 O(m log m)，其中 m 是列表中元素的数量。由于每个建筑物有左右两个边缘，所以 m = 2n，因此这一步的时间复杂度是 O(2n log (2n)) = O(n log n)。

• 接下来，我们遍历排序后的边缘列表，并对优先队列进行操作。优先队列的操作（添加和删除）的时间复杂度是 O(log k)，其中 k 是优先队列中元素的数量。在最坏的情况下，优先队列可能包含所有建筑物的高度，所以 k ≤ n。因此，遍历边缘列表并操作优先队列的时间复杂度是 O(2n log n) = O(n log n)。

综合以上步骤，代码的总时间复杂度是 O(n log n)。

2. 空间复杂度

• 我们使用了一个列表 edges 来存储所有建筑物的左边缘和右边缘，这个列表的大小是 2n，所以空间复杂度是 O(n)。

• 我们使用了一个优先队列 pq 来存储当前所有建筑物的高度。在最坏的情况下，优先队列可能包含所有建筑物的高度，所以空间复杂度是 O(n)。

• 我们使用了一个列表 res 来存储结果，这个列表的大小最多也是 2n，所以空间复杂度是 O(n)。

综合以上步骤，代码的总空间复杂度是 O(n)。

五、总结知识点

• 数据结构：

  • ArrayList：用于存储建筑物的边缘列表和最终的结果列表。
  • PriorityQueue：实现优先队列，用于维护当前所有建筑物的高度，以确定当前的最高点。

• 排序：

  • Collections.sort()：对边缘列表进行排序，使用了自定义的比较器（Comparator）来按照x坐标排序，如果x坐标相同，则按照高度排序。

• 优先队列：

  • PriorityQueue的构造函数中使用了自定义的比较器，以确保队列按高度降序排列（存储负数以实现最大堆效果）。
  • offer()方法：向优先队列中添加元素。
  • peek()方法：获取队列的头部元素，但不移除。
  • remove()方法：从优先队列中移除指定的元素。

• 算法思想：

  • 使用扫描线算法：通过处理每个建筑物的左边缘和右边缘来逐步构建天际线。
  • 使用最大堆（优先队列）来跟踪当前的最高建筑物，以确定天际线上的关键点。

• 逻辑控制：

  • for循环：遍历建筑物的数组以及边缘列表。
  • if语句：判断当前处理的是左边缘还是右边缘，并据此决定是添加还是移除优先队列中的元素。

• 数学运算：

  • 负数的处理：左边缘的高度存储为负数，以便在优先队列中实现最大堆效果。

• 列表操作：

  • Arrays.asList()：创建一个包含给定元素的不可变列表。
  • add()方法：向列表中添加元素。

以上就是解决这个问题的详细步骤，希望能够为各位提供启发和帮助。