LeetCode题练习与总结：生命游戏--289

一、题目描述

根据 百度百科 ， 生命游戏 ，简称为 生命 ，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

1. 如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
2. 如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
3. 如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
4. 如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

示例 1：

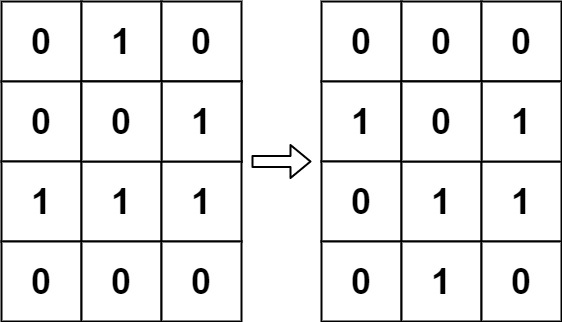
输入：board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出：[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

示例 2：

输入：board = [[1,1],[1,0]]
输出：[[1,1],[1,1]]

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 25
• board[i][j] 为 0 或 1

二、解题思路

1. 遍历面板上的每个细胞，计算每个细胞周围八个位置的活细胞数量。
2. 根据上述四条生存定律，确定每个细胞下一状态是活细胞还是死细胞。
3. 由于细胞的出生和死亡是同时发生的，我们不能直接在原数组上修改细胞状态，否则会影响后续细胞的判断。因此，我们可以使用一个额外的状态，比如用2表示一个活细胞将死亡，用-1表示一个死细胞将复活。
4. 在完成对所有细胞的判断后，再次遍历面板，将状态2转换为0，将状态-1转换为1。

三、具体代码

class Solution {
    public void gameOfLife(int[][] board) {
        int m = board.length;
        int n = board[0].length;
        // 定义方向数组，用于计算八个相邻位置
        int[][] dirs = {{-1, -1}, {-1, 0}, {-1, 1}, {0, -1}, {0, 1}, {1, -1}, {1, 0}, {1, 1}};

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // 计算每个细胞周围八个位置的活细胞数量
                int liveNeighbors = 0;
                for (int[] dir : dirs) {
                    int newRow = i + dir[0];
                    int newCol = j + dir[1];
                    if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && 
                        (board[newRow][newCol] == 1 || board[newRow][newCol] == 2)) {
                        liveNeighbors++;
                    }
                }
                // 根据生存定律判断细胞下一状态
                if (board[i][j] == 1 && (liveNeighbors < 2 || liveNeighbors > 3)) {
                    board[i][j] = 2; // 活细胞将死亡
                }
                if (board[i][j] == 0 && liveNeighbors == 3) {
                    board[i][j] = -1; // 死细胞将复活
                }
            }
        }

        // 更新面板状态
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (board[i][j] == 2) {
                    board[i][j] = 0;
                } else if (board[i][j] == -1) {
                    board[i][j] = 1;
                }
            }
        }
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

• 遍历面板：代码中有两个嵌套的for循环，分别用于遍历面板的行和列。这两个循环分别运行了m次和n次，其中m是面板的行数，n是面板的列数。

• 计算活细胞数量：在第一个嵌套循环内部，还有一个对dirs数组的循环，这个数组的大小是固定的，为8。因此，对于面板上的每个细胞，我们都会执行8次操作来计算周围活细胞的数量。

由于面板上的每个细胞都需要执行固定次数的操作（8次），因此时间复杂度是O(m * n * 8)。由于常数因子在时间复杂度分析中通常被忽略，所以最终的时间复杂度是O(m * n)。

2. 空间复杂度

• 方向数组dirs：这是一个大小为8的二维数组，它的大小是固定的，不随输入面板的大小而变化，因此它对空间复杂度的影响是常数级别的。

• 输入面板board：我们没有使用额外的空间来存储面板的状态，而是直接在原数组上修改。虽然在计算过程中使用了额外的状态（2和-1），但这些状态是在原有数组元素上进行的，没有增加额外的空间。

因此，除了输入面板本身占用的空间外，我们只使用了常数级别的额外空间，所以空间复杂度是O(1)。这里假设修改输入面板的状态不计入额外空间的开销，如果修改输入面板的状态被视为使用额外空间，那么空间复杂度将是O(m * n)。但在大多数情况下，按照常规定义，我们不将输入数据本身的空间计入空间复杂度。

五、总结知识点

1. 二维数组遍历：代码中使用了两个嵌套的for循环来遍历一个二维数组（面板），这是处理二维数据结构的基本技巧。

2. 方向数组：使用了一个二维数组dirs来表示八个可能的移动方向，这是在处理网格问题时常用的方法，用于简化遍历相邻元素的过程。

3. 边界检查：在访问二维数组的相邻元素时，代码中使用了边界检查来确保不会越界，这是编写健壮代码的重要部分。

4. 状态转换：代码中使用了临时状态（2和-1）来表示细胞状态的转换，这是在原地算法（in-place algorithm）中常用的技巧，以避免使用额外的空间。

5. 逻辑判断：根据生命游戏的规则，代码中包含了逻辑判断来确定细胞是生存还是死亡，这涉及到基本的条件语句（if-else）。

6. 原地修改：在更新面板状态时，代码直接在原数组上修改了细胞的状态，这是原地算法的一个例子，可以减少空间复杂度。

7. 数组元素访问：代码中频繁地通过索引访问数组元素，这是处理数组时的基本操作。

以上就是解决这个问题的详细步骤，希望能够为各位提供启发和帮助。