D. Rush Morning（欧拉序+线段树）树的动态直径-CSDN博客

本文链接：https://blog.csdn.net/weixin_62887323/article/details/128667759

文章介绍了在处理树形结构的问题时，欧拉序和DFS序的作用，特别是它们在转化树为线性结构和进行区间操作中的应用。文章以求解树的最大直径为例，阐述了如何利用欧拉序来维护节点间的最近公共祖先（LCA）信息，并通过区间最大值和最小值来优化算法。最后，给出了具体的代码实现，展示了如何在边权修改后求解树的直径并恢复原状。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在写这篇题解之前，我想还是有必要聊一下这道题的关键技术，欧拉序。

首先，是dfs序。dfs序就是在dfs时遍历节点的顺序。

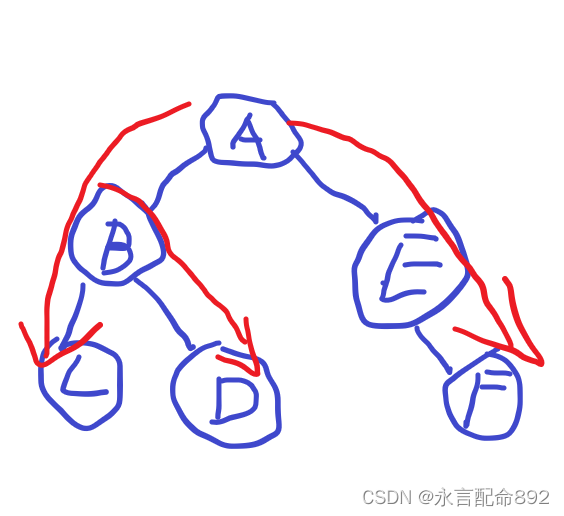
（画的比较抽象）

dfs序的用处在于将树形结构转化为线性结构。以上图为例，遍历顺序为A-B-C-D-E-F。我们会发现B，C，D在同一颗子树上，而在dfs序中，他们表现为一段连续的区间，这样，对原本子树上的操作，如整体加减乘除等等，都可以转化为线性结构上的操作，也就是区间操作，这个时候我们就可以用线段树进行维护了。

除dfs序外，还有一个序列，大体和dfs序差不多，但每个节点进入和离开视为两个点，这种括号序基本可以看作是dfs序的延伸。

当然，树上问题最重要的还是lca，可惜的是dfs序并不能很好的维护两个节点的最近公共祖先的信息，于是我们今天的主角--欧拉序就出来了。

与dfs序不同，每个节点的遍历次数与该节点的度有关，我们能看到，上图的欧拉序为A-B-C-B-D-B-A-E-F-E-A。最后总的序列个数应该为2n-1个。我们发现，和dfs序类似，该节点第一次出现到最后一次出现的区间就是该节点的子树部分，同时任意两个节点之间的路径一定会经过他们的lca，同时我们也能发现lca一定是这个区间深度最低的点。虽然我们因此维护子树和之类的信息变得复杂（因为实际上这些区间不连续了，对于区间求和来说，他存在一些多余的信息需要处理），但是在涉及lca的问题上，反而更加好用。

回到本题，我们发现这题就是给一棵树，然后每次修改一条边的权值，求修改后的最大直径。不过修改完之后就恢复原样。

考虑求树的直径，我们容易得到这样一个式子 $\max_{1\leq u< v\leq n} \left \{ dis[u]+dis[v]-2*dis[lca(u,v)] \right \}$ ，其中，dis表示到根节点的距离。注意到边权都是非负的，那么我们可以说，u，v的区间内最小的dis值一定来自这两个点的lca。想到到这一步我们已经做完了大部分的思想工作。接下来只需要考虑如何维护这个信息。

首先我们需要维护一个区间最大值和一个区间最小值，其中最小值就是lca。但是区间最大值不一定就是u，v，即使是，这里也有两个信息而不是一个。需要指出的是，lca一定在u，v之间，这样的话，我们就可以类似于区间合并一样去写出u，v。不妨假设u小于v，那么我们可以先维护lca-v，以及u-lca的信息，这样我们区间合并时只需要把另一边加上就可以得到一个答案。确切的说，

设lm[p]表示p所指向的子区间中缺少左端点的的最大路径，那么ans=lm[rson]+max[lson]，lm[p]=max[rson]-2*min[lson]。缺少右端点同理。

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=4e5+10,M=2e5+10;
const ll mod=1e9+7;
#define IOS; std::ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
const int inf=1e9+100;

struct node
{
	int l,r;
	ll max,min,lm,rm,ans,lazy;
}t[N<<2];
int tot=0;
int head[N],ver[N<<1],nxt[N<<1],edge[N<<1];
int dep[N];
void add(int u,int v,ll w)
{
	ver[++tot]=v;
	nxt[tot]=head[u];
	edge[tot]=w;
	head[u]=tot;
}
int cn=0,dfn[N],ddfn[N],out[N];
ll d[N];
void dfs(int x,int fa,ll dis)
{
	dfn[++cn]=x;
	ddfn[x]=cn;
	d[x]=dis;
	for(int i=head[x];i;i=nxt[i])
	{
		int y=ver[i];
		if(y==fa)continue;
		dep[y]=dep[x]+1;
		dfs(y,x,dis+edge[i]);
		
		dfn[++cn]=x;
	}
	out[x]=cn;
}
void push_up(int p)
{
	int pr=p<<1;
	t[p].max=max(t[pr].max,t[pr|1].max);
	t[p].min=min(t[pr].min,t[pr|1].min);
	t[p].lm=max(t[pr].lm,t[pr|1].lm);
	t[p].lm=max(t[p].lm,t[pr|1].max-(t[pr].min<<1));
	t[p].rm=max(t[pr].rm,t[pr|1].rm);
	t[p].rm=max(t[p].rm,t[pr].max-(t[pr|1].min<<1));
	t[p].ans=max(t[pr].ans,t[pr|1].ans);
	t[p].ans=max(t[p].ans,max(t[pr].rm+t[pr|1].max,t[pr|1].lm+t[pr].max));
}
void build(int p,int l,int r)
{
	t[p].l=l;t[p].r=r;
	t[p].lazy=0;
	if(l==r)
	{
		t[p].max=t[p].min=d[dfn[l]];
		t[p].lm=t[p].rm=-d[dfn[l]];
		t[p].ans=0;
		return ;
	}
	int mid=(l+r)>>1;
	int pr=p<<1;
	build(pr,l,mid);
	build(pr|1,mid+1,r);
	push_up(p);
}
void push_down(int p)
{
	if(t[p].lazy)
	{
		int pr=p<<1;
		ll w=t[p].lazy;
		t[p].lazy=0;
		t[pr].min+=w;
		t[pr].max+=w;
		t[pr].lm-=w;
		t[pr].rm-=w;
		t[pr].lazy+=w;
		t[pr|1].min+=w;
		t[pr|1].max+=w;
		t[pr|1].lm-=w;
		t[pr|1].rm-=w;
		t[pr|1].lazy+=w;
	}
}
void updata(int p,int l,int r,ll w)
{
	if(l<=t[p].l&&t[p].r<=r)
	{
		t[p].min+=w;
		t[p].max+=w;
		t[p].lm-=w;
		t[p].rm-=w;
		t[p].lazy+=w;
		return ;
	}
	push_down(p);
	int mid=(t[p].l+t[p].r)>>1,pr=p<<1;
	if(l<=mid)updata(pr,l,r,w);
	if(r>mid)updata(pr|1,l,r,w);
	push_up(p);
}
void solve()
{
	int n;cin>>n;
	for(int i=1;i<n;++i)
	{
		int u,v;ll w;
		cin>>u>>v>>w;
		add(u,v,w);
		add(v,u,w);
	}
	dep[1]=0;
	dfs(1,0,0);
	build(1,1,cn);
	int q;cin>>q;
	while(q--)
	{
		int u,v;ll w;
		cin>>u>>v>>w;
		if(dep[u]>dep[v])swap(u,v);
		ll det=w-(d[v]-d[u]);
		updata(1,ddfn[v],out[v],det);
		cout<<t[1].ans<<'\n';
		updata(1,ddfn[v],out[v],-det);
	}
}
int main()
{
	IOS;
	int T=1;
//	cin>>T;
//	scanf("%d",&T);
	while(T--)solve();
	return 0;
}

（文末的碎碎念：我是真没想到边权为0的情况，会导致dep数组和dis数组比较结果的不一致，dis有可能一样，但是dep绝对不一样）