斐波那契数列——C语言

原创已于 2023-09-18 21:17:58 修改 · 2.6w 阅读

282 ·

CC 4.0 BY-SA版权

文章标签：

#c语言 #蓝桥杯 #算法

于 2023-09-18 21:17:02 首次发布

文章介绍了使用递归法、for循环以及结合数组的方法来计算斐波那契数列的第n项。递归法通过递归函数实现，for循环版本则避免了重复计算，数组版本则存储计算结果，展示了不同编程技巧在计算斐波那契数列中的应用。

一、递归法

二、for循环

三、for循环+数组

斐波那契数列（Fibonacci sequence），也称之为黄金分割数列，由意大利数学家列昂纳多・斐波那契（Leonardo Fibonacci）提出。斐波那契数列指的是这样的一个数列：1、1、2、3、5、8、13、21、34、……，这个数列从第 3 项开始，每一项都等于前面两项之和。在数学上，斐波那契数列可以被递推的方法定义如下：

F(1)=1

F(2)=1 *

... ...

F(n)=F(n - 1)+F(n - 2)（n ≥ 3，n ∈ N*）

斐波那契数列是数学上面一个经典的例子，并且在日常生活中有很多应用，他还与黄金分割有着密不可分的联系，而且当 n 趋向于无穷大时，前一项与后一项的比值越来越逼近黄金分割值 0.618。

一、递归法

输出斐波那契数列的第n项

#include<stdio.h>
int Fibon(int n)  //递归函数 
{
   if (n == 1|| n == 2)
       return 1;
   else
       return Fibon(n-1)+ Fibon(n-2);
}

int main()
{
    int n,res=0;
    scanf("%d",&n); 
    for (int i = 1; i <= n; i++)
    {
        res = Fibon(i);
//      printf("%d ",res);
    }
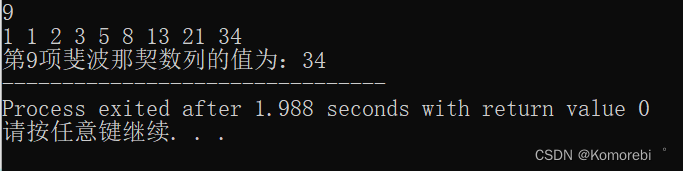
    printf("\n第%d项斐波那契数列的值为：%d",n,res);
    return 0;
}

运行结果：

二、for循环

#include<stdio.h>

int main()
{
    int f1 = 1; //第一项 
    int f2 = 1;  //第二项 
    int f3 = 1;   //如果n=3 才会进入for循环计算，否则都输出1 就不用再分别考虑前面两个数的输出问题 
    int n;
    scanf("%d",&n); 
    for (int i = 2; i < n; i++)
    {
        f3 = f1 + f2;
        f1 = f2;
        f2 = f3;
//      printf("%d ", f3);      
    }
    printf("\n第%d项斐波那契数列的值为：%d",n,f3);
    return 0;
}

三、for循环+数组

#include<stdio.h>
int main()
{
    int a[1005],n;
    scanf("%d",&n);
    
    a[1]=1,a[2]=1,a[3]=2;
    
    for(int i=3;i<=n;i++)
    {
        a[i]=a[i-1]+a[i-2];
//        printf("%d\n",a[i]);
    }
    printf("第%d项斐波那契数列的值为：%d",n,a[n]);
    return 0;
}