XJTUSE-NLP-语法分析

依存语法
理论
在依存语法理论中， “依存”就是指词与词之间支 配与被支配的关系，这种关系不是对等的，而是有方 向的。处于支配地位的成分称为支配者（governor， regent， head），而处于被支配地位的成分称为从属者 （modifier， subordinate， dependency）

两个有向图用带有方向的弧（或称边，edge）来表 示两个成分之间的依存关系，支配者在有向弧的发 出端，被支配者在箭头端，我们通常说被支配者依 存于支配者。
考试只需掌握画线，无需掌握 SBV，VOB，DE…的概念

4 条公理：

1. 一个句子只有一个独立的成分；
2. 句子的其他成分都从属于某一成分；
3. 任何一成分都不能依存于两个或多个成分；
4. 如果成分 A 直接从属于成分 B，而成分 C 在句子中位于 A 和 B 之间，那么，成分 C 或者从属于 A，或 者从属于 B，或者从属于 A 和 B 之间的某一成分。
   对应依存图和依存树的形式约束为：
5. 单一父结点（single headed）
6. 连通（connective）
7. 无环（acyclic）
8. 可投射（projective）
   投射与非投射的概念记清楚！
   在这里插入图片描述

注意：

1. yesterday就不满足公理四，因为which从属于dog但是yesterday没有从属于这二者之间的任何一个单词，而是从属saw
2. 而中文的例子满足投射的定义
   依存语法分析之移进-规约
   自左向右、自底向上的分析算法
   当前分析状态的格局（configuration）是一个三元组： （S， I， A），S， I， A 分别表示栈、未处理结点序列和依存弧 集合。分析体系主要包含两种分析动作组合，一种是 采用标准移进－规约方式，使用 Left-Reduce、Right- Reduce 和 Shift 三种动作。
   理论过于复杂，直接看例子即可：
   
   一共三个操作，移进，左规约，右规约。
   由于该知识点个人理解也不是很到位，公式也比较少，直接把老师 PPT 上的例子照搬过来，进行学习理解即可，考试也是只考类似例题的依存树。
   例题
   例题 1：
   

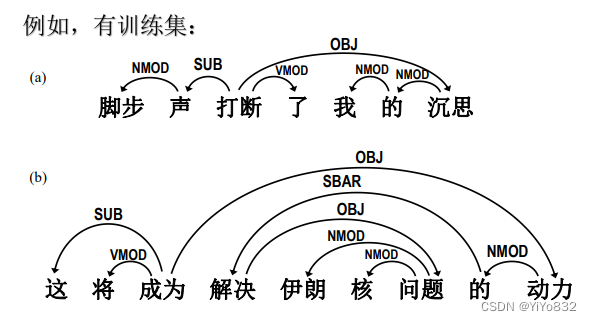
例题 2：

例题 3：
Vinken will join the board as a nonexecutive director Nov 29

个人理解：
因为理论掌握没多少，但对例题可以进行分析

1. 动词为支配者，一般支配一个（多个）名词
2. 形容词一般的支配者应该是后面的名词
3. 介词，语气助词等的支配者一般也为动词
   上下文无关语法
   理论
   Context-free grammars (CFGs)
   编译原理学习过，可以简要过一遍
   假设一个语言是由语法 G 生成的，则 G 可以表示为一个四元组：$$G=(T,N,S,R)$$

• T:表示终结符，句法树的叶子节点
• N：表示非终结符，句法树的非叶子节点
• S：表示为开始符号
• R：重写规则（或者产生式）
  上下文无关特性：句法规则$$X->\lambda$$的应用不依赖于出现在什么上下文环境中
  

Chomsky 范式
一个受 Chomsky 范式约束的 CFG 句法$$G=(T,N,S,R)$$，具有以下形式：

• T:终结符集合
• N：非终结符集合
• S：开始符号
• R：句法规则集合，具有两种形式
  $$N^i\to N^j{N}^{k}for{N}^i\in N,and{N}^j,N^k\in N$$
  $$N^i\to w^{j}for{N}^i\in N,and{w}^j\in T$$
  CYK 句法分析
  自底向上的句法分析算法
  采用一个线图（chart）存储中间结果
  算法步骤：

1. 对于 Chomsky 文法进行范式化
2. 自下而上的分析方法
3. 构造（n+1）*（n+1）的识别矩阵，n 为句子长度，输入句子$$x=w_1,\dots ,w_n$$$$n=|x|$$
4. 识别矩阵，方阵对角线以下全为 0。
5. 主对角线以上元素由文法 G 的非终结符构成。
6. 主对角线上的元素由输入句子的终结符号（单词）构成。
7. 从$$w_1$$开始分析，按平行于主对角线方向，一层一层向上填写矩阵元素$$t_{i}j$$；
   如果存在一个正整数$$k（i+1\le k\le j-1）$$，在文法 G 中有$$A\to BC;B\in t_{i}k,C\in t_{k}j;$$A 写到$$t_{(}i,j)$$位置上。
8. 判断句子 x 由文法 G 所产生的充要条件是：$$t(0,n)=S$$
   给个例子进行理解：
   
   

函数 CYK算法(输入: 词串w, 文法G)
初始化 chart 为一个二维数组，大小为 |w| × |w|，初始值为 空集

对于每个文法规则 R -> s，其中 s 是一个终结符号
    对于每个位置 i，其中 w[i] 是 w 的第 i 个字符
        如果 w[i] == s，则将 R 添加到 chart[i, i]

对于每个子串长度 l，从 2 到 |w|   # 子串长度至少为 2
    对于每个起始位置 i，从 1 到 |w| - l + 1
        对于每个分割位置 k，从 i 到 i + l - 2
            对于每个文法规则 R -> XY，其中 X 和 Y 是非终结符号
                如果 X 在 chart[i, k] 中，且 Y 在 chart[k+1, i+l-1] 中
                    将 R 添加到 chart[i, i+l-1]

如果 文法规则 S -> w 在 chart[1, |w|] 中
    返回 "句子可以由文法生成"
否则
    返回 "句子无法由文法生成"

概率上下文无关文法
理论
G = (T, N, S, R, P)

• T:终结符集合
• N：非终结符集合
• S：开始符号
• R：重写规则
• P：概率函数，为每一个重写规则赋予了一个概率值
  为 CFG 规则下的每一棵句法导出树赋予一个概率。对于句子 s 和其可能的句法导出树集合$$\Gamma (s)$$，PCFG 为$$\Gamma (s)$$中的每棵树 t 赋予一个概率 $$p(t)$$，即得到候选树按照概率的排序。
  $$tre{e}^{\ast }=arg\underset{t\in T(s)}{\max }p(t)$$

举个例子：

HMM vs PCFGs
三个基本任务一致：

1. 计算句子的概率：$$P(w_{1m}|G)$$
2. 为句子找到最优句法树：$$argma{x}_{t}P(t│w_{1m};G)$$
3. 参数学习：求解使得$$P(w_{1m}│G)$$最大的句法 G
   不同之处：
4. HMM 是记录 t 时刻到达状态 j 的最优路径对于的概率（根据概率得到结构）
5. PCFG 可能的导出结构的概率最大值（先得到结构，再计算概率）
   算法
   PPT 上的算法挺复杂的，而且考试不考
   在计算 PCFG 的最优句法结构树，可以先使用 CYK 算法，把所有的语法树构造出来，分别计算概率，然后得出概率最大的语法树！