本文为一个课程设计背景的交通规划设计项目。旨在利用一些机器学习算法+特定交通模型进行规划。
1. 背景
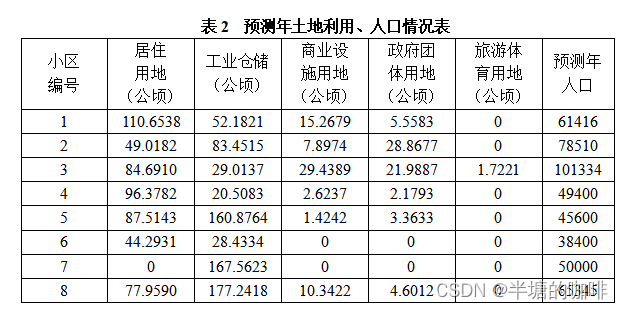
已知某城市规划区域如图1所示,共包含8个交通小区和3条轨道交通线路。已知该规划区域的现状土地利用、人口情况,预测规划年的土地利用、人口情况,交通小区现状OD表,交通小区间公共汽车和轨道交通的效用函数、未来行驶时间和出行费用。具体数据如下表所示。
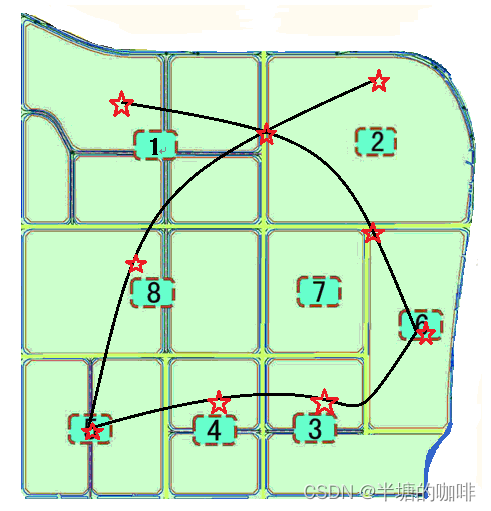
图1 规划区域交通小区分布图

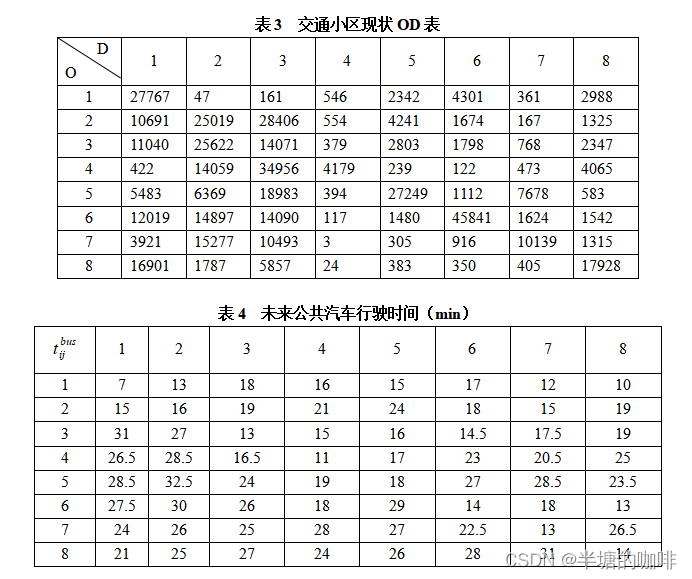
(注:其它数据:票价,行驶时间等详细数据可见后文获取方式)

要求:
1.1 交通发生与吸引量预测
(1)交通发生量
利用现状各交通小区人口数量与调查的现状出行发生量进行分析,从而得出交通发生量的预测模型(如一元线性回归模型),并完成预测年的交通发生量计算。
(2)交通吸引量
根据现状调查不同的出行目的的比例和影响出行的各类土地面积,得到不同土地利用类型的出行吸引率,见图8。假设吸引率不变,计算预测年各交通小区的吸引交通量。
表8 土地类型出行吸引率表(人次/公顷)
| 土地类型 | 居住 | 工业(仓储) | 商业设施 | 政府团体 | 旅游、体育 |
| 吸引率 | 100 | 120 | 3900 | 3500 | 20 |
(3)若各小区的交通发生量之和不等于交通吸引量之和,则用调整系数法进行调整,并运用matlab软件进行编程实现该方法。
1.2 交通分布预测:
采用福莱特法进行交通分布预测,从而得到规划区内的OD分布交通量(容许误差为 3%),并利用matlab软件进行算法编程设计实现分布预测。
1.3 交通方式划分预测
采用二元Logit模型进行交通方式划分,并运用matlab软件设计完成交通方式划分,从而分别得到各交通小区预测年公共汽车和轨道交通的OD分布交通量。
2. 解决方案:
本文的交通分配建模与设计的流程图如下图2所示:
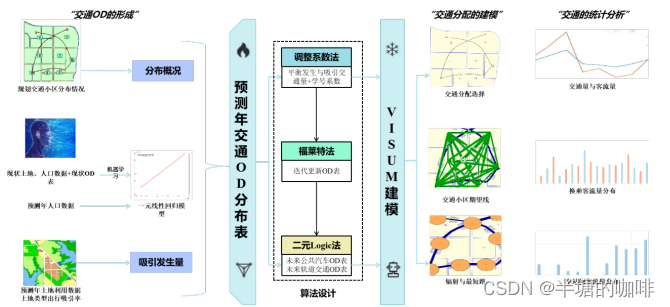
图2 交通分配建模与设计流程
2.1 出行产生预测
2.1.1 计算过程
此部分的算法伪代码为:
| Algorithm:一元线性回归模型 |
| 定义:自变量,现状年人口;因变量:现状年出行交通发生量; 输入:“现状人口、现状OD、预测人口” 主要工具:Excel Step 1:模型参数的确立 采用最小二乘估计法作为模型参数训练的基础算法; Step 2:模型应用 利用上述训练得到的最终的一元线性回归模型,对预测年出行交通发生量进行预测,将预测年人口作为自变量,预测年出行交通发生量作为因变量完成模型应用环节。 输出:“预测OD” |
根据上述算法设计步骤,得到本文预测年出行交通发生量一元线性回归模型,其相关表达式如下:
| (1) |
最终预测结果可见表9所示。
表9 预测年出行发生量
| 小区 | 预测年人口(X矩阵) | 预测年出行产生(Y矩阵) |
| 1 | 61416 | 77962 |
| 2 | 78510 | 98437 |
| 3 | 101334 | 125776 |
| 4 | 49400 | 63570 |
| 5 | 45600 | 59018 |
| 6 | 38400 | 50394 |
| 7 | 50000 | 64288 |
| 8 | 65345 | 82668 |
同样,我们也可以利用EXCEL去实现这个算法,结果也是一样的,可见下图

2.2 出行吸引预测
表10 土地类型出行吸引率表(人次/公顷)
| 土地类型 | 居住 | 工业(仓储) | 商业设施 | 政府团体 | 旅游、体育 |
| 吸引率(%) | 100 | 120 | 3900 | 3500 | 20 |
表11 预测年土地利用矩阵
| 小区编号 | 居住用地(公顷) | 工业仓储 (公顷) | 商业设施用地(公顷) | 政府团体用地(公顷) | 旅游体育用地(公顷) |
| 1 | 110.6538 | 52.1821 | 15.2679 | 5.5583 | 0 |
| 2 | 49.0182 | 83.4515 | 7.8974 | 28.8677 | 0 |
| 3 | 84.6910 | 29.0137 | 29.4389 | 21.9887 | 1.7221 |
| 4 | 96.3782 | 20.5083 | 2.6237 | 2.1793 | 0 |
| 5 | 87.5143 | 160.8764 | 1.4242 | 3.3633 | 0 |
| 6 | 44.2931 | 28.4334 | 0 | 0 | 0 |
| 7 | 0 | 167.5623 | 0 | 0 | 0 |
| 8 | 77.9590 | 177.2418 | 10.3422 | 4.6012 | 0 |
2.2.1 计算过程
| Algorithm:矩阵运算 |
| 输入:“土地类型出行吸引率表(人次/公顷)、预测年土地利用矩阵” 主要工具:Excel Step 1:运算 利用EXCEL的PRODUCT函数对输入的两个矩阵进行乘法预算,得到预测年出行交通吸引量数据 Step 2:数据检验 由于MATLAB拥有强大的矩阵运算功能,因此本文利用MATLAB对上述得到的数据进行数值检验,检验结果显示无误。 输出:“预测OD” |
最终得到的预测年出行交通吸引量如表12所示。

2.2.2 数据集成
将一、二中得到的预测年出行交通发生量与吸引量进行数据集成,得到如表13所示的预测年OD矩阵表。
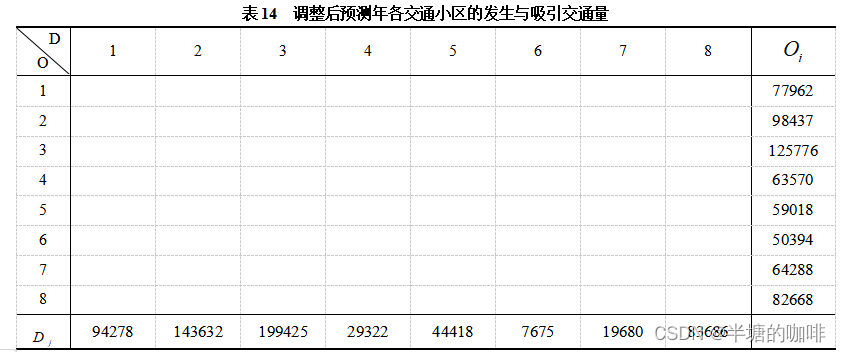
表13 预测年各交通小区的发生与吸引交通量

2.3 针对交通发生与吸引量不均衡的调整系数法
调整系数法的基本步骤
以交通发生量之和为基底,对交通吸引量各值进行调整,调整公式为

由此,使用MATLAB进行数值运算,得到调整后预测年各交通小区的发生与吸引交通量集成的OD矩阵表,见表14所示。
2.4 基于福莱特法的交通分布划分
2.4.1 计算过程:
福莱特法的算法流程如图4所示

该方法相关计算公式有

利用MatLab或者EXCEL均可实现迭代,迭代次数为3次,这里就不占用篇幅展示了。展示下其中的代码:
主要呢,使用到了嵌套循环计算与判别,只是公式里面的i和j并非编程时按照公式原封不动就敲上去了,这个还是有些区别的(当时在这卡了一段时间T_T)
for j = 1:n
for i =1:n
a(i,j) = q(j,i) * F_d(i);
b(i,j) = q(i,j) * F_o(i);
end
Li(j) = O3(j) / sum(a(:,j));
Lj(j) = D3(j) / sum(b(:,j));
end
for i_new = 1:n
for j_new = 1:n
f(i_new,j_new) = 0.5 * (Li(i_new)+Lj(j_new)) * F_o(i_new) * F_d(j_new);
q(i_new,j_new) = f(i_new,j_new) * q(i_new,j_new)
end
end
O3 = sum(q,2)';
D3 = sum(q,1);计算过程与收敛判定:满足后,即可停止迭代
至此,得到最终的交通OD表。
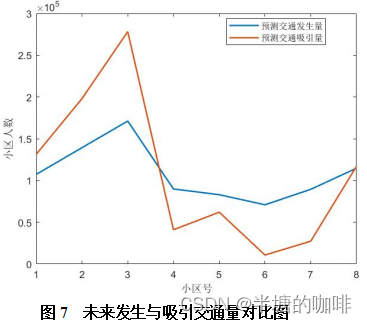
2.4.2 交通分布现状与预测结果图表及文字分析:
通过先前计算,后续可进行结果分析。本文基于上述福莱特法之后的预测结果结合先前现状交通量进行对比分析,主要分析如下。
(这里就不用文字说明了,可视化是很基本的操作了,只展示部分图片,要想获取完整报告可见文末获取方式。)



2.5 基于二元Logic法的交通方式划分
二元Logic模型的相关计算公式有
(1)效用函数计算公式为

(2)方式划分率计算公式为

(3)预测年OD分布交通量计算公式为


2.6 交通分配
这部分属于Visum的场景建模了,不属于算法的部分,本文不再赘述,想具体了解此部分的,可见文末完整报告的获取方式。
3. 扩展研究(列车运行图的可视化分析;发车间隔、换乘时间、票价的影响等)
这部分属于额外的研究。我主要也是想锻炼下编matlab代码的能力,涉及到将时间参量导入并可视化的一些训练。主要用到的函数为:
filename = '列车发车(停站).xlsx';
sheet = 1;
range = 'A:H';
[num, txt, raw] = xlsread(filename, sheet, range);
% 提取日期时间数据的原始数字值(小数)
timeData = cell2mat(raw(:, 2:8));
% 将原始数字值转换为日期时间格式
timeData = datetime(timeData, 'ConvertFrom', 'excel');代码解释:第一部分为基本的数据导入,xlsread函数导入了excel表格数据。后面的含有时间数据,是需要经过数据类型转换的,因为上面的函数导入数据默认不读取文本型数据,字符型数据格式为double型,因此需要用cellmat函数和datetime函数进行转换。
数据搞定,后续就是一些基操了,可视化结果展示其中一张,如下:

4. 部分代码展示
算法部分:
%%问题一交通发生量——一元线性回归模型%%
data1 = xlsread("现状人口+出行发生量.xlsx");
x = data1(1:8,7);
y = data1(1:8,8);
coeff = polyfit(x, y, 1);
alpha1 = coeff(1);
beta1 = coeff(2);
y_0 = alpha1 * x + beta1;
correlation_matrix = corrcoef(x, y);
correlation = correlation_matrix(1, 2);
r = correlation^2;
disp(['R-squared: ', num2str(r)]);
x_p = data1(:,9);
y_p = alpha1 * x_p + beta1
k = O2_sum / D2_sum * xuehao_xishu
O2_new = O2 * xuehao_xishu;
D2_new = D2 * k;
%将结果写入表内%
T_0 = zeros(9);
T_0(1:8,9) = O2_new;
T_0(9,1:8) = D2_new;
T = table(T_0)
%%问题二分布预测——福莱特方法%%
X = xlsread("福莱特方法过程表.xlsx");
q = X(2:9,2:9);
U3 = O2_new' ;
V3 = D2_new' ;
n=size(q,1);
O3 = X(2:9,10)';
D3 = X(10,2:9) ;
O_now = O3;
D_now = D3;
plot(O_now,'LineWidth',1.5);
hold on
plot(D_now,'LineWidth',1.5);
hold off
xlabel('小区号');
ylabel('小区人数');
legend('现状交通发生量','现状交通吸引量','Location',"best");
F_o = U3 ./ O3;
F_d = V3 ./ D3;
for j = 1:n
for i =1:n
a(i,j) = q(j,i) * F_d(i);
b(i,j) = q(i,j) * F_o(i);
end
Li(j) = O3(j) / sum(a(:,j));
Lj(j) = D3(j) / sum(b(:,j));
end
for i_new = 1:n
for j_new = 1:n
f(i_new,j_new) = 0.5 * (Li(i_new)+Lj(j_new)) * F_o(i_new) * F_d(j_new);
q(i_new,j_new) = f(i_new,j_new) * q(i_new,j_new)
end
end
O3 = sum(q,2)';
D3 = sum(q,1);
%%问题三交通方式划分——二元Logit模型%%
data4 = xlsread("未来行驶时间、票价.xlsx");
data5 = xlsread("未来OD.xlsx");
OD_future = data5(2:9,2:9);
%未来公交汽车行驶时间数据矩阵%
bus_time = data4(2:9,2:9);
%未来轨道交通行驶时间数据矩阵%
sub_time = data4(14:21,2:9);
%未来公交汽车票价数据矩阵%
bus_fare = data4(2:9,12:19);
%未来轨道交通票价数据矩阵%
sub_fare = data4(14:21,12:19);
运行图部分:
filename = '列车发车(停站).xlsx';
sheet = 1;
range = 'A:H';
[num, txt, raw] = xlsread(filename, sheet, range);
% 提取日期时间数据的原始数字值(小数)
timeData = cell2mat(raw(:, 2:8));
% 将原始数字值转换为日期时间格式
timeData = datetime(timeData, 'ConvertFrom', 'excel');
% 绘制列车运行图
figure;
hold on;
grid on;
plot(x1,y1,'LineWidth',1.5)
plot(x2,y2,'LineWidth',1.5)
% legend('上行第一班','上行第二班','上行第三班','下行第三班','下行第二班','下行第一班')
hold off5. 文末结语
本文到这基本就结束了,上面就是本文的大体框架,想深入研究这个项目的可以联系博主获取完整解决方案报告及其MatLab代码和Excel程序。
联系方式:


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








