一.多元分析
- 聚类分析
最短距离法+聚类图
【1】Q型聚类(样本)
(1)样本之间
闵氏距离:
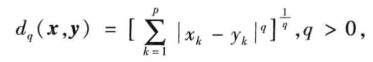
注意量纲要相同,避免多重相关性
马氏距离:
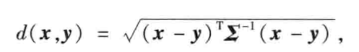
其中,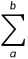 是p维总体Z的协方差矩阵
是p维总体Z的协方差矩阵
不受量纲的影响
(2)聚类之间
离差平方和法:

(3)相关命令
X=zsore(X) 标准化处理
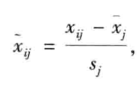
Y=pdist(X,metric) 用metric的方法计算矩阵中对象的距离(闵氏距离增加一个指数值)
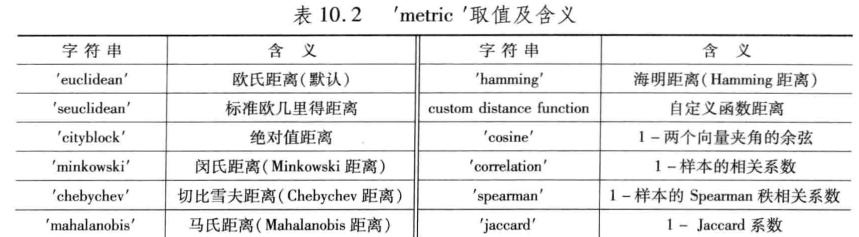
Z=linkage(Y,method) 生成聚类树

(4)案例:销售能力
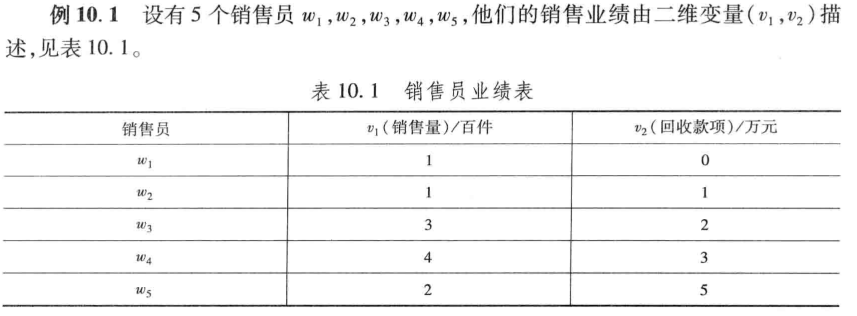
绝对值距离
clc,clear
a=[1,0;1,1;3,2;4,3;2,5];
[m,n]=size(a);
d=zeros(m);
d=mandist(a'); %mandist求矩阵列向量组之间的两两绝对值距离
d=tril(d); %截取下三角元素
nd=nonzeros(d); %去掉d中的零元素,非零元素按列排列
nd=union([],nd) %去掉重复的非零元素
for i=1:m-1
nd_min=min(nd);
[row,col]=find(d==nd_min);tm=union(row,col); %row和col归为一类
tm=reshape(tm,1,length(tm)); %把数组tm变成行向量
fprintf('第%d次合成,平台高度为%d时的分类结果为:%s\n',...
i,nd_min,int2str(tm));
nd(nd==nd_min)=[]; %删除已经归类的元素
if length(nd)==0
break
end
end
第1次合成,平台高度为1时的分类结果为:1 2
第2次合成,平台高度为2时的分类结果为:3 4
第3次合成,平台高度为3时的分类结果为:2 3
第4次合成,平台高度为4时的分类结果为:1 3 4 5matlab统计工具箱
clc,clear
a=[1,0;1,1;3,2;4,3;2,5];
y=pdist(a,'cityblock'); %求a的两两行向量间的绝对值距离
yc=squareform(y) %变换成距离方阵
z=linkage(y) %产生等级聚类树
dendrogram(z) %画聚类图
T=cluster(z,'maxclust',3) %把对象划分成3类
for i=1:3
tm=find(T==i); %求第i类的对象
tm=reshape(tm,1,length(tm)); %变成行向量
fprintf('第%d类的有%s\n',i,int2str(tm)); %显示分类结果
end
第1类的有1 2
第2类的有3 4
第3类的有5
【2】R型聚类(指标)
(1)变量相似性度量
相关系数
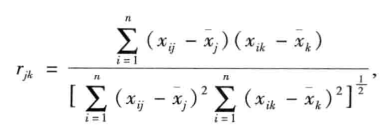
夹角余弦
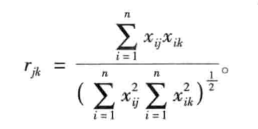
(2)指标聚类的解释性



clc,clear
a=textread('ch.txt');a(isnan(a))=0;
d=1-abs(a); %进行数据变换,把相关系数转化为距离
d=tril(d); %提出d矩阵的下三角部分
b=nonzeros(d);%去掉d中的零元素
b=b'; %化成行向量
z=linkage(b,'complete'); %按最长距离法聚类
y=cluster(z,'maxclust',2) %把变量划分成两类
ind1=find(y==1);ind1=ind1' %显示第一类对应的变量标号
ind2=find(y==2);ind2=ind2' %显示第二类对应的变量标号
h=dendrogram(z); %画聚类图
set(h,'Color','k','LineWidth',1.3) %把聚类图线的颜色改成黑色,线宽加粗
ind1 =
1 2 8 9 10 11 12
ind2 =
3 4 5 6 7 13 14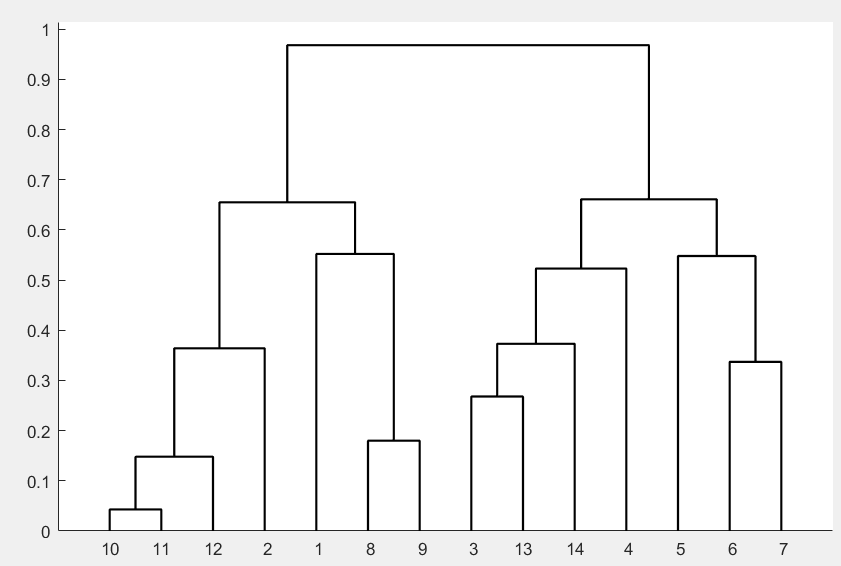
(3)案例:各地教育水平

R型聚类分析:(10个指标分成6类)
clc, clear
a=load('gj.txt'); %把原始数据保存在纯文本文件gj.txt中
b=zscore(a); %数据标准化
r=corrcoef(b) %计算相关系数矩阵
%d=tril(1-r); d=nonzeros(d)'; %另外一种计算距离方法
d=pdist(b','correlation'); %计算相关系数导出的距离
z=linkage(d,'average'); %按类平均法聚类
h=dendrogram(z); %画聚类图
set(h,'Color','k','LineWidth',1.3) %把聚类图线的颜色改成黑色,线宽加粗
T=cluster(z,'maxclust',6) %把变量划分成6类
for i=1:6
tm=find(T==i); %求第i类的对象
tm=reshape(tm,1,length(tm)); %变成行向量
fprintf('第%d类的有%s\n',i,int2str(tm)); %显示分类结果
end
第1类的有1
第2类的有2 3 4 5 6
第3类的有9
第4类的有7
第5类的有8
第6类的有10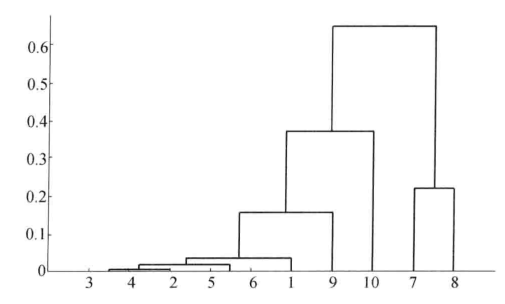
Q型聚类分析:(30个地区分成3/4/5类)
clc,clear
load gj.txt %把原始数据保存在纯文本文件gj.txt中
gj(:,[3:6])=[]; %删除数据矩阵的第3列~第6列,即使用变量1,2,7,8,9,10
gj=zscore(gj); %数据标准化
y=pdist(gj); %求对象间的欧氏距离,每行是一个对象
z=linkage(y,'average'); %按类平均法聚类
h=dendrogram(z); %画聚类图
set(h,'Color','k','LineWidth',1.3) %把聚类图线的颜色改成黑色,线宽加粗
for k=3:5
fprintf('划分成%d类的结果如下:\n',k)
T=cluster(z,'maxclust',k); %把样本点划分成k类
for i=1:k
tm=find(T==i); %求第i类的对象
tm=reshape(tm,1,length(tm)); %变成行向量
fprintf('第%d类的有%s\n',i,int2str(tm)); %显示分类结果
end
if k==5
break
end
fprintf('**********************************\n');
end
划分成3类的结果如下:
第1类的有25
第2类的有2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 26 27 28 29 30
第3类的有1
**********************************
划分成4类的结果如下:
第1类的有2 3
第2类的有4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 26 27 28 29 30
第3类的有25
第4类的有1
**********************************
划分成5类的结果如下:
第1类的有28 29 30(宁夏、贵州、青海)
第2类的有4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 26 27
第3类的有2 3(上海、天津)
第4类的有25(西藏)
第5类的有1(北京)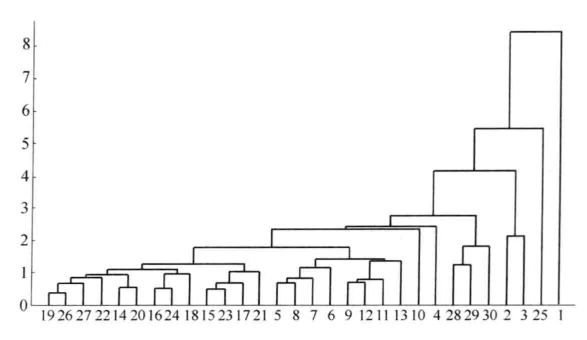
- 主成分分析
【1】方法


特征值大小排序,求贡献率


【2】回归分析
最小二乘法对选取主成分后的模型参数进行估计,再变换回原来的模型求出参数估计

clc,clear
load sn.txt %把原始的x1,x2,x3,x4,y的数据保存在纯文本文件sn.txt中
[m,n]=size(sn);
x0=sn(:,[1:n-1]);y0=sn(:,n);
hg1=[ones(m,1),x0]\y0; %计算普通最小二乘法回归系数
hg1=hg1' %变成行向量显示回归系数,其中第1个分量是常数项,其它按x1,...,xn排序
fprintf('y=%f',hg1(1)); %开始显示普通最小二乘法回归结果
for i=2:n
if hg1(i)>0
fprintf('+%f*x%d',hg1(i),i-1);
else
fprintf('%f*x%d',hg1(i),i-1)
end
end
fprintf('\n')
r=corrcoef(x0) %计算相关系数矩阵
xd=zscore(x0); %对设计矩阵进行标准化处理
yd=zscore(y0); %对y0进行标准化处理
[vec1,lamda,rate]=pcacov(r) %vec1为r的特征向量,lamda为r的特征值,rate为各个主成分的贡献率
f=repmat(sign(sum(vec1)),size(vec1,1),1); %构造与vec1同维数的元素为±1的矩阵
vec2=vec1.*f %修改特征向量的正负号,使得特征向量的所有分量和为正
contr=cumsum(rate) %计算累积贡献率,第i个分量表示前i个主成分的贡献率
df=xd*vec2; %计算所有主成分的得分
num=input('请选项主成分的个数:') %通过累积贡献率交互式选择主成分的个数
hg21=df(:,[1:num])\yd %主成分变量的回归系数,这里由于数据标准化,回归方程的常数项为0
hg22=vec2(:,1:num)*hg21 %标准化变量的回归方程系数
hg23=[mean(y0)-std(y0)*mean(x0)./std(x0)*hg22, std(y0)*hg22'./std(x0)] %计算原始变量回归方程的系数
fprintf('y=%f',hg23(1)); %开始显示主成分回归结果
for i=2:n
if hg23(i)>0
fprintf('+%f*x%d',hg23(i),i-1);
else
fprintf('%f*x%d',hg23(i),i-1);
end
end
fprintf('\n')
%下面计算两种回归分析的剩余标准差
rmse1=sqrt(sum((hg1(1)+x0*hg1(2:end)'-y0).^2)/(m-n)) %拟合了n个参数
rmse2=sqrt(sum((hg23(1)+x0*hg23(2:end)'-y0).^2)/(m-num)) %拟合了num个参数
不做主成分分析,直接线性回归
hg1 =
62.4054 1.5511 0.5102 0.1019 -0.1441
y=62.405369+1.551103*x1+0.510168*x2+0.101909*x3-0.144061*x4
相关系数矩阵
r =
1.0000 0.2286 -0.8241 -0.2454
0.2286 1.0000 -0.1392 -0.9730
-0.8241 -0.1392 1.0000 0.0295
-0.2454 -0.9730 0.0295 1.0000
特征值
lamda =
2.2357
1.5761
0.1866
0.0016
贡献率
rate =
55.8926
39.4017
4.6652
0.0406
请选项主成分的个数:3
主成分回归分析后的线性回归方程
hg21 =
0.6570
0.0083
0.3028
变回标准化变量的回归方程
hg22 =
0.5130
0.2787
-0.0608
-0.4229
变回原来变量的回归方程
hg23 =
85.7433 1.3119 0.2694 -0.1428 -0.3801
y=85.743263+1.311890*x1+0.269419*x2-0.142765*x3-0.380075*x4【3】案例:各地教育水平
clc,clear
load gj.txt %把原始数据保存在纯文本文件gj.txt中
gj=zscore(gj); %数据标准化
r=corrcoef(gj); %计算相关系数矩阵
%下面利用相关系数矩阵进行主成分分析,vec1的列为r的特征向量,即主成分的系数
[vec1,lamda,rate]=pcacov(r) %lamda为r的特征值,rate为各个主成分的贡献率
contr=cumsum(rate) %计算累积贡献率
f=repmat(sign(sum(vec1)),size(vec1,1),1);%构造与vec1同维数的元素为±1的矩阵
vec2=vec1.*f %修改特征向量的正负号,使得每个特征向量的分量和为正
num=4; %num为选取的主成分的个数
df=gj*vec2(:,1:num); %计算各个主成分的得分
tf=df*rate(1:num)/100; %计算综合得分
[stf,ind]=sort(tf,'descend'); %把得分按照从高到低的次序排列
stf=stf', ind=ind'
特征值
lamda =
7.5022
1.5770
0.5362
0.2064
0.1450
0.0222
0.0071
0.0027
0.0007
0.0006
累加贡献率
contr =
75.0216
90.7915
96.1536
98.2174
99.6674
99.8893
99.9605
99.9870
99.9943
100.0000
10个中选取前4个
标准化变量前4个主成分的特征向量(列)
vec2 =
0.3497 -0.1972 -0.1639 -0.1022
0.3590 0.0343 -0.1084 -0.2266
0.3623 0.0291 -0.0900 -0.1692
0.3623 0.0138 -0.1128 -0.1607
0.3605 -0.0507 -0.1534 -0.0442
0.3602 -0.0646 -0.1645 -0.0032
0.2241 0.5826 -0.0397 0.0812
0.1201 0.7021 0.3577 0.0702
0.3192 -0.1941 0.1204 0.8999
0.2452 -0.2865 0.8637 -0.2457
y1=0.3497x1+0.3590x2+...+0.2452x10
贡献率作为权重,得到综合评价值的计算公式
Z= 0.75022y1+ 0.15770y2+ 0.05362y3+ 0.02064y4
代入各地4个主成分值
综合评价值及排名
stf =
列 1 至 12
8.6043 4.4738 2.7881 0.8119 0.7621 0.5884 0.2971 0.2455 0.0581 0.0058 -0.2680 -0.3645
列 13 至 24
-0.4879 -0.5065 -0.7016 -0.7428 -0.7697 -0.7965 -0.8895 -0.8917 -0.9557 -0.9610 -1.0147 -1.1246
列 25 至 30
-1.1470 -1.2059 -1.2250 -1.2513 -1.6514 -1.6800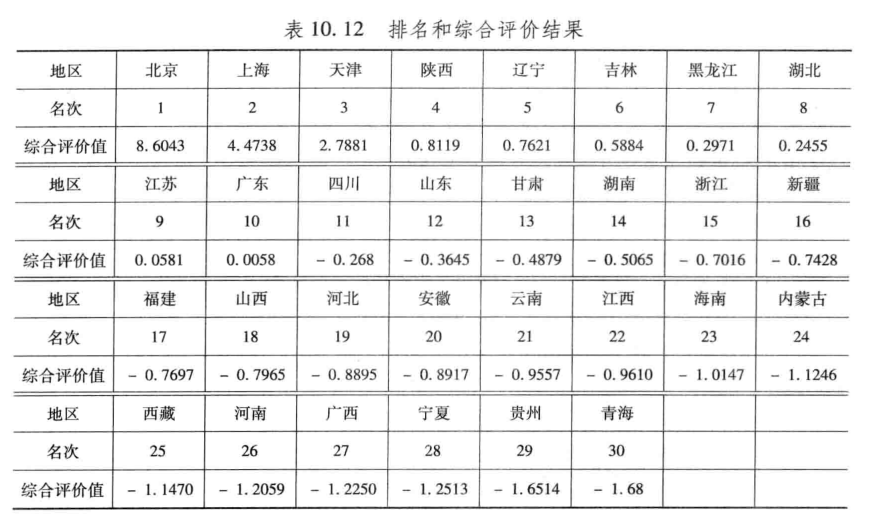
- 因子分析
【1】模型


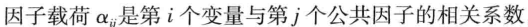

【2】因子载荷矩阵的估计方法

(1)主成分分析法求因子分析模型

clc,clear
r=[1 1/5 -1/5;1/5 1 -2/5;-1/5 -2/5 1];
%下面利用相关系数矩阵求主成分解,val的列为r的特征向量,即主成分的系数
[vec,val,con]=pcacov(r) %val为r的特征值,con为各个主成分的贡献率
num=input('请选择公共因子的个数:'); %交互式选取主因子的个数
f1=repmat(sign(sum(vec)),size(vec,1),1);
vec=vec.*f1; %特征向量正负号转换
f2=repmat(sqrt(val)',size(vec,1),1);
a=vec.*f2 %计算因子载荷矩阵
aa=a(:,1:num) %提出两个主因子的载荷矩阵
s1=sum(aa.^2) %计算对X的贡献率,实际上等于对应的特征值
s2=sum(aa.^2,2) %计算共同度
特征向量
vec =
0.4597 0.8881 0
0.6280 -0.3251 0.7071
-0.6280 0.3251 0.7071
特征值
val =
1.5464
0.8536
0.6000
贡献率
con =
51.5470
28.4530
20.0000
请选择公共因子的个数:2
载荷矩阵
a =
0.5717 0.8205 0
0.7809 -0.3003 0.5477
-0.7809 0.3003 0.5477
aa =
0.5717 0.8205
0.7809 -0.3003
-0.7809 0.3003
F1、F2对X的贡献率
s1 =
1.5464 0.8536
共同度
s2 =
1.0000
0.7000
0.7000(2)主因子分析法求因子载荷矩阵


clc,clear
r=[1 1/5 -1/5;1/5 1 -2/5;-1/5 -2/5 1];
n=size(r,1); rt=abs(r); %求矩阵r所有元素的绝对值
rt(1:n+1:n^2)=0; %把rt矩阵的对角线元素换成0
rstar=r; %R*初始化
rstar(1:n+1:n^2)=max(rt'); %把矩阵rstar的对角线元素换成rt矩阵各行的最大值
%下面利用R*矩阵求主因子解,vec1的列为矩阵rstar的特征向量
[vec1,val,rate]=pcacov(rstar) %val为rstar的特征值,rate为各个主成分的贡献率
f1=repmat(sign(sum(vec1)),size(vec1,1),1);
vec2=vec1.*f1 %特征向量正负号转换
f2=repmat(sqrt(val)',size(vec2,1),1);
a=vec2.*f2 %计算因子载荷矩阵
num=input('请选择公共因子的个数:'); %交互式选取主因子的个数
aa=a(:,1:num) %提出num个因子的载荷矩阵
s1=sum(aa.^2) %计算对X的贡献率
s2=sum(aa.^2,2) %计算共同度
R*特征向量
vec1 =
0.3690 0.9294 0
0.6572 -0.2610 0.7071
-0.6572 0.2610 0.7071
R*特征值
val =
0.9123
0.0877
0.0000
贡献率
rate =
91.2311
8.7689
0.0000
vec2 =
0.3690 0.9294 0
0.6572 -0.2610 0.7071
-0.6572 0.2610 0.7071
因子载荷矩阵
a =
0.3525 0.2752 0
0.6277 -0.0773 0.0000
-0.6277 0.0773 0.0000
请选择公共因子的个数:2
主因子载荷矩阵
aa =
0.3525 0.2752
0.6277 -0.0773
-0.6277 0.0773
s1 =
0.9123 0.0877
约相关系数矩阵R*对角线元素
s2 =
0.2000
0.4000
0.4000(3)最大似然估计法求因子载荷矩阵
clc,clear
r=[1 1/5 -1/5;1/5 1 -2/5;-1/5 -2/5 1];
[Lambda,Psi] = factoran(r,1,'xtype','cov')
最大似然估计法只能求得一个主因子,对应因子的载荷矩阵为
Lambda =
0.3162
0.6325
-0.6325
特殊方差
Psi =
0.9000
0.6000
0.6000【3】因子旋转
(1)方法


(2)案例

clc,clear
r=[1 -1/3 2/3;-1/3 1 0;2/3 0 1];
%下面利用相关系数矩阵求主成分解,vec1的列为r的特征向量,即主成分的系数
[vec1,val,rate]=pcacov(r) %val为r的特征值,rate为各个主成分的贡献率
f1=repmat(sign(sum(vec1)),size(vec1,1),1); %构造与vec1同维数的元素为±1的矩阵
vec2=vec1.*f1; %修改特征向量的正负号,每个特征向量乘以所有分量和的符号函数值
f2=repmat(sqrt(val)',size(vec2,1),1);
lambda=vec2.*f2 %构造全部因子的载荷矩阵,见(10.27)式
num=2; %选择两个主因子
[lambda2,t]=rotatefactors(lambda(:,1:num),'method', 'varimax') %对载荷矩阵进行旋转
%其中lambda2为旋转载荷矩阵,t为变换的正交矩阵
vec1 =
0.7071 0 0.7071
-0.3162 0.8944 0.3162
0.6325 0.4472 -0.6325
val =
1.7454
1.0000
0.2546
rate =
58.1785
33.3333
8.4881
因子载荷矩阵
lambda =
0.9342 0 0.3568
-0.4178 0.8944 0.1596
0.8355 0.4472 -0.3192
取前2个因子
旋转后的因子载荷矩阵
lambda2 =
0.8706 -0.3386
-0.0651 0.9850
0.9408 0.1139
正交矩阵
t =
0.9320 -0.3625
0.3625 0.9320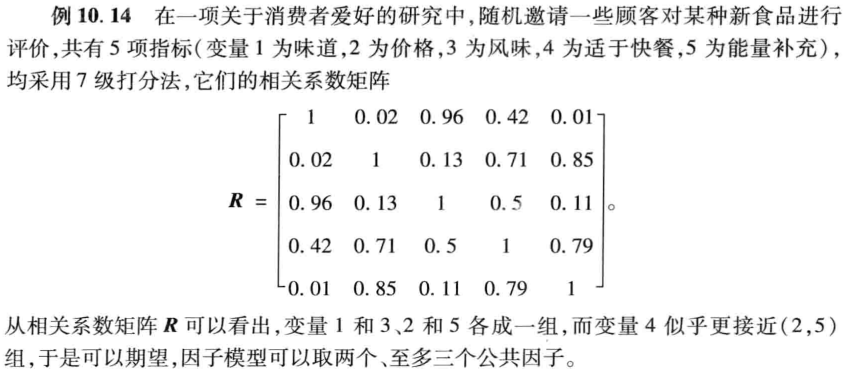
clc,clear
r=[1 0.02 0.96 0.42 0.01; 0.02 1 0.13 0.71 0.85; 0.96 0.13 1 0.5 0.11
0.42 0.71 0.5 1 0.79; 0.01 0.85 0.11 0.79 1];
[vec1,val,rate]=pcacov(r)
f1=repmat(sign(sum(vec1)),size(vec1,1),1);
vec2=vec1.*f1; %特征向量正负号转换
f2=repmat(sqrt(val)',size(vec2,1),1);
a=vec2.*f2 %计算全部因子的载荷矩阵,见(10.27)式
num=2; %num为因子的个数
a1=a(:,[1:num]) %提出两个因子的载荷矩阵
tcha=diag(r-a1*a1') %因子的特殊方差
gtd1=sum(a1.^2,2) %求因子载荷矩阵a1的共同度
con=cumsum(rate(1:num)) %求累积贡献率
[B,T]=rotatefactors(a1,'method','varimax')%B为旋转因子载荷矩阵,T为正交矩阵
gtd2=sum(B.^2,2) %求因子载荷矩阵B的共同度
w=[sum(a1.^2), sum(B.^2)] %分别计算两个因子载荷矩阵对应的方差贡献
vec1 =
0.3315 0.6072 0.0985 0.1387 -0.7018
0.4602 -0.3900 0.7426 -0.2821 -0.0717
0.3821 0.5565 0.1684 0.1170 0.7087
0.5560 -0.0781 -0.6016 -0.5682 -0.0017
0.4726 -0.4042 -0.2205 0.7514 -0.0090
val =
2.8531
1.8063
0.2045
0.1024
0.0337
rate =
57.0618
36.1266
4.0898
2.0482
0.6735
取m=2
因子载荷
a =
0.5599 0.8161 0.0445 0.0444 0.1288
0.7773 -0.5242 0.3358 -0.0903 0.0132
0.6453 0.7479 0.0762 0.0374 -0.1301
0.9391 -0.1049 -0.2720 -0.1818 0.0003
0.7982 -0.5432 -0.0997 0.2405 0.0017
a1 =
0.5599 0.8161
0.7773 -0.5242
0.6453 0.7479
0.9391 -0.1049
0.7982 -0.5432
未旋转时的特殊方差
tcha =
0.0205
0.1211
0.0241
0.1071
0.0678
共同度
gtd1 =
0.9795
0.8789
0.9759
0.8929
0.9322
累计贡献
con =
57.0618
93.1885
旋转后的因子载荷矩阵
B =
0.0198 0.9895
0.9374 -0.0113
0.1286 0.9795
0.8425 0.4280
0.9654 -0.0157
正交矩阵
T =
0.8357 0.5491
-0.5491 0.8357
旋转后的共同度
gtd2 =
0.9795
0.8789
0.9759
0.8929
0.9322
分别计算两个因子载荷矩阵对应的方差贡献
w =
2.8531 1.8063 2.5375 2.1220
【4】案例
(1)上市公司赢利能力和资本结构
clc,clear
load ssgs.txt %把原始数据保存在纯文本文件ssgs.txt中
n=size(ssgs,1);
x=ssgs(:,[1:4]); y=ssgs(:,5); %分别提出自变量x1...x4和因变量x的值
x=zscore(x); %数据标准化
r=corrcoef(x) %求相关系数矩阵
[vec1,val,con1]=pcacov(r) %进行主成分分析的相关计算
f1=repmat(sign(sum(vec1)),size(vec1,1),1);
vec2=vec1.*f1; %特征向量正负号转换
f2=repmat(sqrt(val)',size(vec2,1),1);
a=vec2.*f2 %求初等载荷矩阵
num=input('请选择主因子的个数:'); %交互式选择主因子的个数
am=a(:,[1:num]); %提出num个主因子的载荷矩阵
[bm,t]=rotatefactors(am,'method', 'varimax') %am旋转变换,bm为旋转后的载荷阵
bt=[bm,a(:,[num+1:end])]; %旋转后全部因子的载荷矩阵,前两个旋转,后面不旋转
con2=sum(bt.^2) %计算因子贡献
check=[con1,con2'/sum(con2)*100]%该语句是领会旋转意义,con1是未旋转前的贡献率
rate=con2(1:num)/sum(con2) %计算因子贡献率
coef=inv(r)*bm %计算得分函数的系数
score=x*coef %计算各个因子的得分
weight=rate/sum(rate) %计算得分的权重
Tscore=score*weight' %对各因子的得分进行加权求和,即求各企业综合得分
[STscore,ind]=sort(Tscore,'descend') %对企业进行排序
display=[score(ind,:)';STscore';ind'] %显示排序结果
[ccoef,p]=corrcoef([Tscore,y]) %计算F与资产负债的相关系数
[d,dt,e,et,stats]=regress(Tscore,[ones(n,1),y]);%计算F与资产负债的方程
d,stats %显示回归系数,和相关统计量的值
请选择主因子的个数:2
该语句是领会旋转意义,con1是未旋转前的贡献率
check =
47.4292 44.4859
38.7400 41.6833
9.8255 9.8255
4.0052 4.0052
贡献率
rate =
0.4449 0.4168
综合因子得分公式
F=(44.49F1+41.68F2)/44.49+41.68
各个因子得分函数
coef =
0.5060 -0.0450
0.1615 0.5151
-0.1831 0.5810
0.5015 -0.0199
F1=0.5060x1+0.1615x2+...
F2=...
score =
1.5159 -0.5814
0.0025 1.4477
1.2477 -0.9729
1.2791 -0.1564
-0.6094 0.1544
0.0315 1.4691
-1.7266 0.2639
0.9313 -1.1949
0.9789 0.3959
-1.2509 -0.7424
0.4558 0.8548
-0.9859 0.3468
-0.0351 0.3166
-0.8910 -1.6131
-0.0563 1.3577
-0.8872 -1.3459
weight =
0.5163 0.4837
Tscore =
0.5014
0.7016
0.1735
0.5847
-0.2399
0.7269
-0.7637
-0.0972
0.6969
-1.0049
0.6488
-0.3412
0.1350
-1.2403
0.6277
-1.1091
STscore =
0.7269
0.7016
0.6969
0.6488
0.6277
0.5847
0.5014
0.1735
0.1350
-0.0972
-0.2399
-0.3412
-0.7637
-1.0049
-1.1091
-1.2403
排名
ind =
6
2
9
11
15
4
1
3
13
8
5
12
7
10
16
14
排名按照行
信息按照列:F1、F2、F、公司在表格中的顺序
display =
列 1 至 12
0.0315 0.0025 0.9789 0.4558 -0.0563 1.2791 1.5159 1.2477 -0.0351 0.9313 -0.6094 -0.9859
1.4691 1.4477 0.3959 0.8548 1.3577 -0.1564 -0.5814 -0.9729 0.3166 -1.1949 0.1544 0.3468
0.7269 0.7016 0.6969 0.6488 0.6277 0.5847 0.5014 0.1735 0.1350 -0.0972 -0.2399 -0.3412
6.0000 2.0000 9.0000 11.0000 15.0000 4.0000 1.0000 3.0000 13.0000 8.0000 5.0000 12.0000
列 13 至 16
-1.7266 -1.2509 -0.8872 -0.8910
0.2639 -0.7424 -1.3459 -1.6131
-0.7637 -1.0049 -1.1091 -1.2403
7.0000 10.0000 16.0000 14.0000
ccoef =
1.0000 -0.6987
-0.6987 1.0000
p =
1.0000 0.0026
0.0026 1.0000
因子分析法的回归方程
F=0.8290-0.0268y
d =
0.8290
-0.0268
stats =
0.4882 13.3524 0.0026 0.2745(2)生育率影响因素
clc,clear
load sy.txt %把原始数据保存在纯文本文件sy.txt中
sy=zscore(sy); %数据标准化
r=cov(sy); %求标准化数据的协方差阵,即求相关系数矩阵
[vec1,val,con]=pcacov(r) %进行主成分分析的相关计算
f1=repmat(sign(sum(vec1)),size(vec1,1),1);
vec2=vec1.*f1; %特征向量正负号转换
f2=repmat(sqrt(val)',size(vec2,1),1);
a=vec2.*f2 %求初等载荷矩阵
num=input('请选择主因子的个数:'); %交互式选择主因子的个数
am=a(:,[1:num]); %提出num个主因子的载荷矩阵
[b,t]=rotatefactors(am,'method', 'varimax') %旋转变换,b为旋转后的载荷阵
bt=[b,a(:,[num+1:end])]; %旋转后全部因子的载荷矩阵
degree=sum(b.^2,2) %计算共同度
contr=sum(bt.^2) %计算因子贡献
rate=contr(1:num)/sum(contr) %计算因子贡献率
coef=inv(r)*b %计算得分函数的系数
请选择主因子的个数:2
共同度
degree =
0.8845
0.9114
0.8598
0.8779
0.9301
contr =
2.6806 1.7831 0.2516 0.1841 0.1006
rate =
0.5361 0.3566
旋转后得分函数
coef =
0.0421 0.5104
-0.1850 -0.6284
0.3434 0.0322
0.3781 0.1003
0.3936 0.1134最大似然法
clc,clear
load sy.txt %把原始数据保存在纯文本文件sy.txt中
num=input('请选择主因子的个数:'); %交互式选择主因子的个数
[lambda,psi,T,stats,F]=factoran(sy,num,'rotate','varimax','scores','regression')
%Lambda返回的是因子载荷矩阵,psi返回的是特殊方差,T返回的是旋转正交矩阵,stats返回的是一些统计量,F返回的是因子得分矩阵
gtd=1-psi %计算共同度
contr=sum(lambda.^2) %计算可解释方差
请选择主因子的个数:24.判别分析

clc,clear
a=[9 7 8 8 9 8 7 4 3 6 2 1 6 8 2
8 6 7 5 9 9 5 4 6 3 4 2 4 1 4
7 6 8 5 3 7 6 4 6 3 5 2 5 3 5];
train=a(:,[1:12])'; %提出已知样本点数据,这里进行了矩阵转置
sample=a(:,[13:end])'; %提出待判样本点数据
group=[ones(7,1);2*ones(5,1)]; %已知样本的分类
[x1,y1]=classify(sample,train,group,'mahalanobis') %马氏距离分类
[x2,y2]=classify(sample,train,group,'linear') %线性分类
[x3,y3]=classify(sample,train,group,'quadratic') %二次分类
%函数classify的第二个返回值为误判率
x1 =
1
1
2
y1 =
0
x2 =
1
1
2
y2 =
0
x3 =
1
1
2
y3 =
0
5.典型相关分析
【1】基本思想

【2】案例:职业满意度

clc,clear
load r.txt %原始的相关系数矩阵保存在纯文本文件r.txt中
n1=5;n2=7;num=min(n1,n2);
s1=r([1:n1],[1:n1]); %提出X与X的相关系数
s12=r([1:n1],[n1+1:end]); %提出X与Y的相关系数
s21=s12'; %提出Y与X的相关系数
s2=r([n1+1:end],[n1+1:end]); %提出Y与Y的相关系数
m1=inv(s1)*s12*inv(s2)*s21; %计算矩阵M1,式(10.60)
m2=inv(s2)*s21*inv(s1)*s12; %计算矩阵M2,式(10.60)
[vec1,val1]=eig(m1); %求M1的特征向量和特征值
for i=1:n1
vec1(:,i)=vec1(:,i)/sqrt(vec1(:,i)'*s1*vec1(:,i)); %特征向量归一化,满足a's1a=1
vec1(:,i)=vec1(:,i)/sign(sum(vec1(:,i))); %特征向量乘以1或-1,保证所有分量和为正
end
val1=sqrt(diag(val1)); %计算特征值的平方根
[val1,ind1]=sort(val1,'descend'); %按照从大到小排列
a=vec1(:,ind1(1:num)) %取出X组的系数阵
dcoef1=val1(1:num) %提出典型相关系数
flag=1; %把计算结果写到Excel中的行计数变量
xlswrite('bk.xls',a,'Sheet1','A1') %把计算结果写到Excel文件中去
flag=n1+2; str=char(['A',int2str(flag)]); %str为Excel中写数据的起始位置
xlswrite('bk.xls',dcoef1','Sheet1',str)
[vec2,val2]=eig(m2);
for i=1:n2
vec2(:,i)=vec2(:,i)/sqrt(vec2(:,i)'*s2*vec2(:,i)); %特征向量归一化,满足b's2b=1
vec2(:,i)=vec2(:,i)/sign(sum(vec2(:,i))); %特征向量乘以1或-1,保证所有分量和为正
end
val2=sqrt(diag(val2)); %计算特征值的平方根
[val2,ind2]=sort(val2,'descend'); %按照从大到小排列
b=vec2(:,ind2(1:num)) %取出Y组的系数阵
dcoef2=val2(1:num) %提出典型相关系数
flag=flag+2; str=char(['A',int2str(flag)]); %str为Excel中写数据的起始位置
xlswrite('bk.xls',b,'Sheet1',str)
flag=flag+n2+1; str=char(['A',int2str(flag)]); %str为Excel中写数据的起始位置
xlswrite('bk.xls',dcoef2','Sheet1',str)
x_u_r=s1*a %x,u的相关系数
y_v_r=s2*b %y,v的相关系数
x_v_r=s12*b %x,v的相关系数
y_u_r=s21*a %y,u的相关系数
flag=flag+2; str=char(['A',int2str(flag)]);
xlswrite('bk.xls',x_u_r,'Sheet1',str)
flag=flag+n1+1; str=char(['A',int2str(flag)]);
xlswrite('bk.xls',y_v_r,'Sheet1',str)
flag=flag+n2+1; str=char(['A',int2str(flag)]);
xlswrite('bk.xls',x_v_r,'Sheet1',str)
flag=flag+n1+1; str=char(['A',int2str(flag)]);
xlswrite('bk.xls',y_u_r,'Sheet1',str)
mu=sum(x_u_r.^2)/n1 %x组原始变量被u_i解释的方差比例
mv=sum(x_v_r.^2)/n1 %x组原始变量被v_i解释的方差比例
nu=sum(y_u_r.^2)/n2 %y组原始变量被u_i解释的方差比例
nv=sum(y_v_r.^2)/n2 %y组原始变量被v_i解释的方差比例
fprintf('X组的原始变量被u1~u%d解释的比例为%f\n',num,sum(mu));
fprintf('Y组的原始变量被v1~v%d解释的比例为%f\n',num,sum(nv));
X组的原始变量被u1~u5解释的比例为1.000000
Y组的原始变量被v1~v5解释的比例为0.802974【3】案例:城市竞争力与基础设施
clc,clear
load x.txt %原始的x组的数据保存在纯文本文件x.txt中
load y.txt %原始的y组的数据保存在纯文本文件y.txt中
p=size(x,2);q=size(y,2);
x=zscore(x);y=zscore(y); %标准化数据
n=size(x,1); %观测数据的个数
%下面做典型相关分析,a1,b1返回的是典型变量的系数,r返回的是典型相关系数
%u1,v1返回的是典型变量的值,stats返回的是假设检验的一些统计量的值
[a1,b1,r,u1,v1,stats]=canoncorr(x,y)
%下面修正a1,b1每一列的正负号,使得a,b每一列的系数和为正
%对应的,典型变量取值的正负号也要修正
a=a1.*repmat(sign(sum(a1)),size(a1,1),1)
b=b1.*repmat(sign(sum(b1)),size(b1,1),1)
u=u1.*repmat(sign(sum(a1)),size(u1,1),1)
v=v1.*repmat(sign(sum(b1)),size(v1,1),1)
x_u_r=x'*u/(n-1) %计算x,u的相关系数
y_v_r=y'*v/(n-1) %计算y,v的相关系数
x_v_r=x'*v/(n-1) %计算x,v的相关系数
y_u_r=y'*u/(n-1) %计算y,u的相关系数
ux=sum(x_u_r.^2)/p %x组原始变量被u_i解释的方差比例
ux_cum=cumsum(ux) %x组原始变量被u_i解释的方差累积比例
vx=sum(x_v_r.^2)/p %x组原始变量被v_i解释的方差比例
vx_cum=cumsum(vx) %x组原始变量被v_i解释的方差累积比例
vy=sum(y_v_r.^2)/q %y组原始变量被v_i解释的方差比例
vy_cum=cumsum(vy) %y组原始变量被v_i解释的方差累积比例
uy=sum(y_u_r.^2)/q %y组原始变量被u_i解释的方差比例
uy_cum=cumsum(uy) %y组原始变量被u_i解释的方差累积比例
val=r.^2 %典型相关系数的平方,M1或M2矩阵的非零特征值6.对应分析
【1】案例:消费结构


clc, clear
a=load('xf.txt'); %原始文件保存在纯文本文件xf.txt中
T=sum(sum(a));
P=a/T; %计算对应矩阵P
r=sum(P,2), c=sum(P) %计算边缘分布
Row_prifile=a./repmat(sum(a,2),1,size(a,2)) %计算行轮廓分布阵
B=(P-r*c)./sqrt((r*c)); %计算标准化数据B
[u,s,v]= svd(B,'econ') %对标准化后的数据阵B作奇异值分解
w1=sign(repmat(sum(v),size(v,1),1)) %修改特征向量的符号矩阵,使得v中的每一个列向量的分量和大于0
w2=sign(repmat(sum(v),size(u,1),1)) %根据v对应地修改u的符号
vb=v.*w1 %修改特征向量的正负号
ub=u.*w2 %修改特征向量的正负号,本例中样本点个数和变量个数不等
lamda=diag(s).^2 %计算Z'*Z的特征值,即计算主惯量
ksi2square=T*(lamda) %计算卡方统计量的分解
T_ksi2square=sum(ksi2square) %计算总卡方统计量
con_rate=lamda/sum(lamda) %计算贡献率
cum_rate=cumsum(con_rate) %计算累积贡献率
beta=diag(r.^(-1/2))*ub; %求加权特征向量
G=beta*s %求行轮廓坐标
alpha=diag(c.^(-1/2))*vb; %求加权特征向量
F=alpha*s %求列轮廓坐标F
num1=size(G,1); %样本点的个数
rang=minmax(G(:,[1,2])'); %坐标的取值范围
delta=(rang(:,2)-rang(:,1))/(5*num1); %画图的标注位置调整量
ch={'A', 'B', 'C', 'D', 'E', 'F', 'G'};
yb={'山西','内蒙古','辽宁','吉林','黑龙江','海南','四川','贵州','甘肃','青海'};
hold on
plot(G(:,1),G(:,2),'*','Color','k','LineWidth',1.3) %画行点散布图
text(G(:,1)-delta(1),G(:,2)-3*delta(2),yb) %对行点进行标注
plot(F(:,1),F(:,2),'H','Color','k','LineWidth',1.3) %画列点散布图
text(F(:,1)+delta(1),F(:,2),ch) %对列点进行标注
xlabel('dim1'), ylabel('dim2')
xlswrite('tt',[diag(s),lamda,ksi2square,con_rate,cum_rate])
%把计算结果输出到Excel文件,这样便于把数据直接贴到word中的表格
ind1=find(G(:,1)>0); %根据行坐标第一维进行分类
rowclass=yb(ind1) %提出第一类样本点
ind2=find(F(:,1)>0); %根据列坐标第一维进行分类
colclass=ch(ind2) %提出第一类变量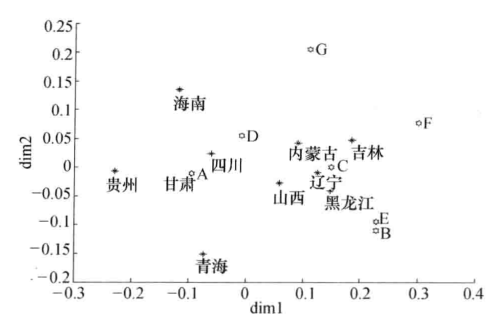


【2】案例:品牌定位
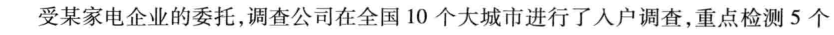

clc,clear
a=[543 342 453 609 261 360 243 183
245 785 630 597 311 233 108 69
300 200 489 740 365 324 327 228
401 396 395 693 350 309 263 143
147 117 410 726 366 447 329 420];
a_i_dot=sum(a,2) %计算行和
a_dot_j=sum(a) %计算列和
T=sum(a_i_dot) %计算数据的总和
P=a/T; %计算对应矩阵P
r=sum(P,2), c=sum(P) %计算边缘分布
Row_prifile=a./repmat(sum(a,2),1,size(a,2)) %计算行轮廓分布阵
B=(P-r*c)./sqrt((r*c)); %计算标准化数据B
[u,s,v]=svd(B,'econ') %对标准化后的数据阵B作奇异值分解
w1=sign(repmat(sum(v),size(v,1),1)) %修改特征向量的符号矩阵
%使得v中的每一个列向量的分量和大于0
w2=sign(repmat(sum(v),size(u,1),1)); %根据v对应地修改u的符号
vb=v.*w1; %修改特征向量的正负号
ub=u.*w2; %修改特征向量的正负号
lamda=diag(s).^2 %计算Z'*Z的特征值,既计算惯量
ksi2square=T*(lamda) %计算卡方统计量的分解
T_ksi2square=sum(ksi2square) %计算总卡方统计量
con_rate=lamda/sum(lamda) %计算贡献率
cum_rate=cumsum(con_rate) %计算累积贡献率
beta=diag(r.^(-1/2))*ub; %求加权特征向量
G=beta*s %求行轮廓坐标G
alpha=diag(c.^(-1/2))*vb; %求加权特征向量
F=alpha*s %求列轮廓坐标F
num1=size(G,1); %样本点的个数
rang=minmax(G(:,[1 2])'); %行坐标的取值范围
delta=(rang(:,2)-rang(:,1))/(4*num1); %画图的标注位置调整量
chrow={'A', 'B', 'C', 'D', 'E'};
strcol={'少男','少女','白领','工人','农民','士兵','主管','教授'};
hold on
plot(G(:,1),G(:,2),'*','Color','k','LineWidth',1.3) %画行点散布图
text(G(:,1),G(:,2)-delta(2),chrow) %对行点进行标注
plot(F(:,1),F(:,2),'H','Color','k','LineWidth',1.3) %画列点散布图
text(F(:,1)-delta(1),F(:,2)+1.2*delta(2),strcol) %对列点进行标注
xlabel('dim1'), ylabel('dim2')
xlswrite('tt',[diag(s),lamda,ksi2square,con_rate,cum_rate])
%把计算结果输出到Excel文件,这样便于把数据直接贴到word中的表格
dd=dist(G(:,1:2),F(:,1:2)') %计算第一个矩阵的行向量与第二个矩阵的列向量之间的距离
行轮廓坐标G =
-0.0267 0.2231 0.0766 -0.0212 0.0000
-0.4790 -0.1590 0.0155 -0.0100 0.0000
0.1644 0.0064 -0.0915 -0.0495 0.0000
-0.0559 0.0946 -0.0554 0.0654 0.0000
0.3992 -0.1663 0.0540 0.0160 0.0000
列轮廓坐标F =
-0.0975 0.3986 0.0349 -0.0036 0.0000
-0.6147 -0.1062 0.0379 0.0386 0.0000
-0.1334 -0.0753 -0.0001 -0.0837 0.0000
0.0724 -0.0188 -0.0510 0.0112 -0.0000
0.0639 -0.0673 -0.0776 0.0320 0.0000
0.1923 0.0010 0.0799 0.0212 -0.0000
0.3049 0.0490 -0.0792 0.0013 0.0000
0.5269 -0.1601 0.1345 0.0057 0.0000
距离dd =
0.1893 0.6740 0.3169 0.2614 0.3041 0.3119 0.3745 0.6733
0.6756 0.1456 0.3556 0.5689 0.5507 0.6902 0.8111 1.0060
0.4716 0.7872 0.3088 0.0954 0.1246 0.0285 0.1468 0.3990
0.3069 0.5938 0.1867 0.1712 0.2013 0.2653 0.3636 0.6360
0.7522 1.0157 0.5403 0.3586 0.3496 0.2660 0.2350 0.1279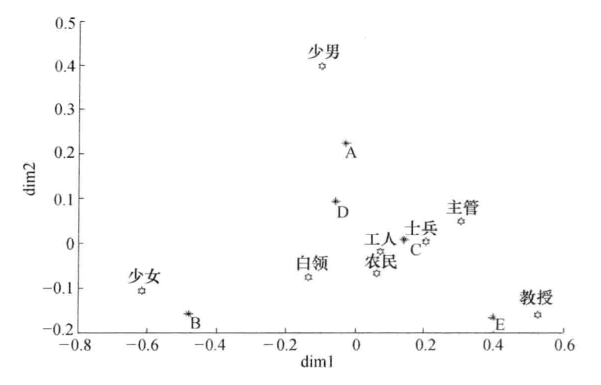

7.多维标度法
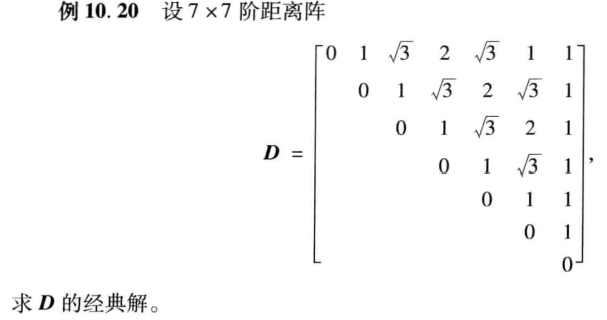
【1】案例:距离矩阵的六边形解
clc, clear
D=[0, 1, sqrt(3), 2, sqrt(3), 1, 1; zeros(1,2),1, sqrt(3), 2, sqrt(3), 1
zeros(1,3),1, sqrt(3), 2, 1;zeros(1,4), 1, sqrt(3), 1
zeros(1,5), 1, 1; zeros(1,6), 1; zeros(1,7)] %原始距离矩阵的上三角元素
d=D+D'; %构造完整的距离矩阵
%d=nonzeros(D')'; %转换成pdist函数输出格式的数据
[y,eigvals]=cmdscale(d) %求经典解,d可以为实对称矩阵或pdist函数的行向量输出
plot(y(:,1),y(:,2),'o','Color','k','LineWidth',1.3) %画出点的坐标
%下面我们通过求特征值求经典解
D2=D+D'; %构造对称距离矩阵
A=-D2.^2/2; %构造A矩阵
n=size(A,1);
H=eye(n)-ones(n)/n; %构造H矩阵
B=H*A*H %构造B矩阵
[vec1,val1]=eig(B); %求B矩阵的特征向量vec1和特征值val1
[val2,ind]=sort(diag(val1),'descend') %把特征按从大到小排列
vec2=vec1(:,ind) %相应地把特征向量也重新排序
vec3=orth(vec2(:,[1,2])); %构造正交特征向量
point=[vec3(:,1)*sqrt(val2(1)),vec3(:,2)*sqrt(val2(2))] %求点的坐标
hold on
plot(point(:,1),point(:,2),'D','Color','k','LineWidth',1.3) %验证得到的解和Matlab不一致
theta=0.409; %旋转的角度
T=[cos(theta),-sin(theta);sin(theta),cos(theta)];
Tpoint=point*T; %把特征向量进行一个正交变换
plot(Tpoint(:,1),Tpoint(:,2),'+','Color','k','LineWidth',1.3) %验证这样得到的解和Matlab一致
legend('Matlab命令cmdscale求得的解','按照算法求得的一个解','正交变换后得到的与cmdscale相同的解','Location','best')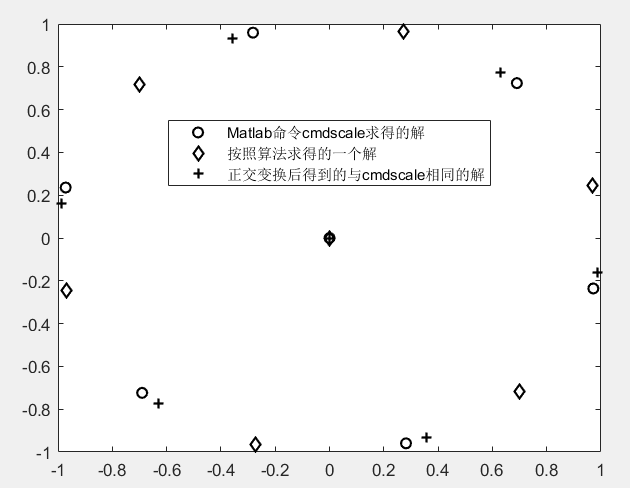

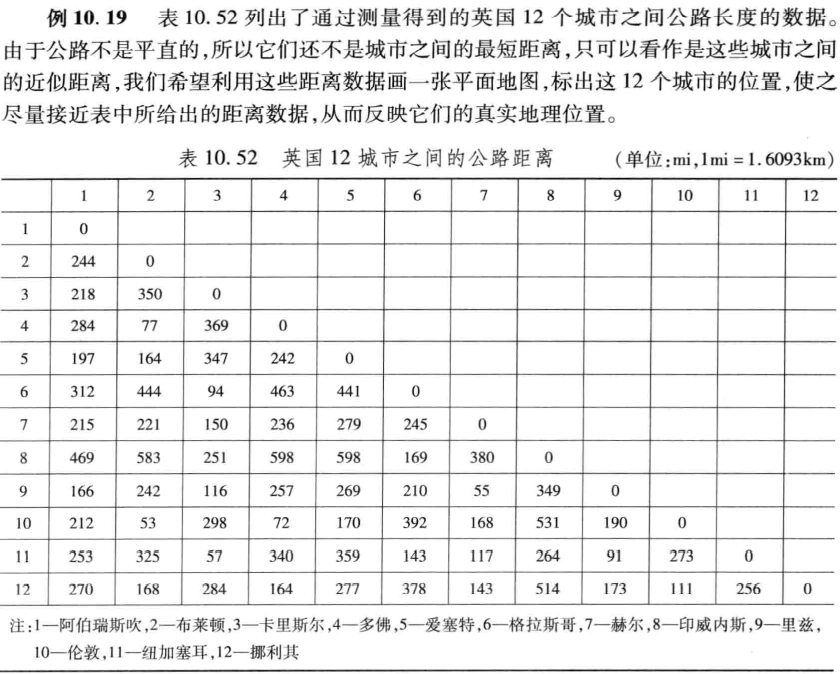
【2】案例:距离推地图
clc, clear
d=textread('d.txt'); %把原始数据保存在纯文本文件d.txt中
d=nonzeros(d)'; %按照列顺序提出矩阵d中的非零元素,再化成行向量
cities={'1.阿伯瑞斯吹','2.布莱顿','3.卡里斯尔','4.多佛','5.爱塞特',...
'6.格拉斯哥','7.赫尔','8.印威内斯','9.里兹','10.伦敦',...
'11.纽加塞耳','12.挪利其'} %构造细胞数组
[y,eigvals]=cmdscale(d) %求经典解,这里d为实对称阵或pdist格式的行向量
plot(y(:,1),y(:,2),'o','Color','k','LineWidth',1.5) %画出点的坐标
text(y(:,1)-18,y(:,2)-12,cities); %对点进行标注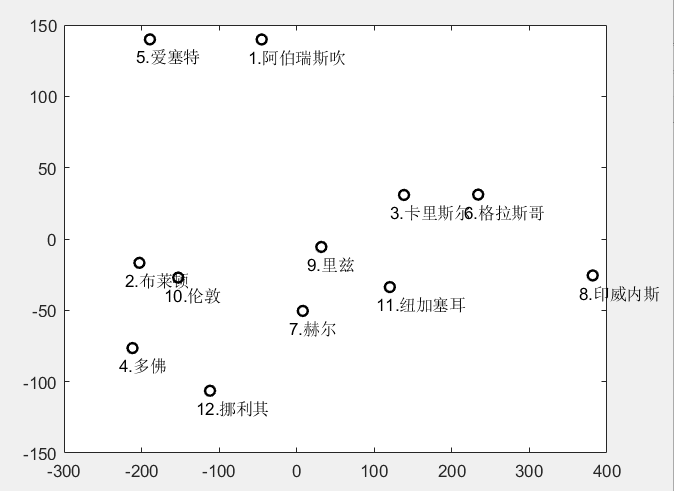
二.综合评价与决策
1.TOPSIS
【1】流程
(1)数据预处理(属性规范化)
a.线性变换
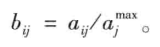
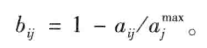
b.标准0-1变换
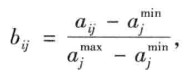
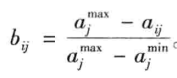
c.区间变换
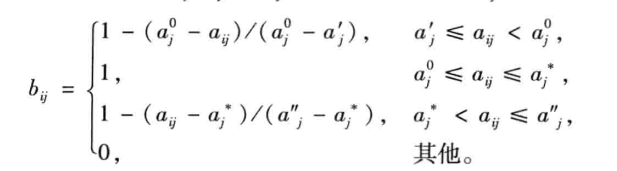
d.向量规范化
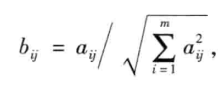
e.标准化处理
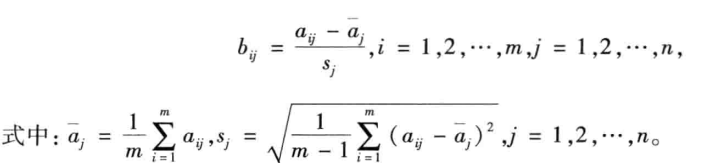
(2)评价
设定权重向量,构造加权规范阵
确定正负理想解
计算到理想解的距离
计算排序指标值
排序
【2】案例:研究生教育评估
clc, clear
a=[0.1 5 5000 4.7
0.2 6 6000 5.6
0.4 7 7000 6.7
0.9 10 10000 2.3
1.2 2 400 1.8];
[m,n]=size(a);
x2=@(qujian,lb,ub,x)(1-(qujian(1)-x)./(qujian(1)-lb)).*(x>=lb & x<qujian(1))+(x>=qujian(1) & x<=qujian(2))+(1-(x-qujian(2))./(ub-qujian(2))).*(x>qujian(2) & x<=ub);
qujian=[5,6]; lb=2; ub=12;
a(:,2)=x2(qujian,lb,ub,a(:,2)); %对属性2进行变换
for j=1:n
b(:,j)=a(:,j)/norm(a(:,j)); %向量规划化
end
w=[0.2 0.3 0.4 0.1];
c=b.*repmat(w,m,1); %求加权矩阵
Cstar=max(c); %求正理想解
Cstar(4)=min(c(:,4)) %属性4为成本型的
C0=min(c); %q求负理想解
C0(4)=max(c(:,4)) %属性4为成本型的
for i=1:m
Sstar(i)=norm(c(i,:)-Cstar); %求到正理想解的距离
S0(i)=norm(c(i,:)-C0); %求到负理想的距离
end
f=S0./(Sstar+S0);
[sf,ind]=sort(f,'descend') %求排序结果
正理想解
Cstar =
0.1530 0.1791 0.2759 0.0174
负理想解
C0 =
0.0128 0 0.0110 0.0648
排序指标
sf =
0.7003 0.6255 0.5787 0.5258 0.3165
排序
ind =
4 3 2 1 52.模糊综合评判
案例:二级指标人事考评
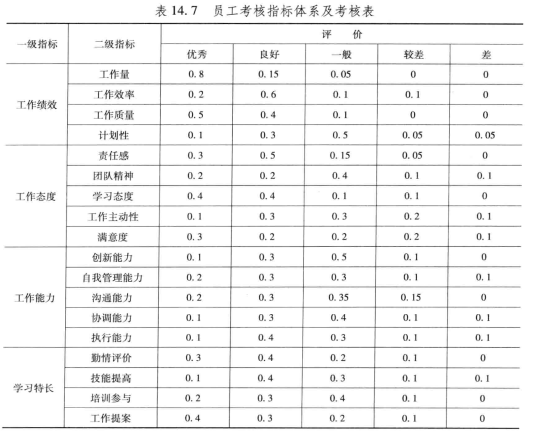
clc, clear
a=load('mhdata.txt');
%一级指标权重
w=[0.4 0.3 0.2 0.1];
%二级指标权重
w1=[0.2 0.3 0.3 0.2];
w2=[0.3 0.2 0.1 0.2 0.2];
w3=[0.1 0.2 0.3 0.2 0.2];
w4=[0.3 0.2 0.2 0.3];
b(1,:)=w1*a([1:4],:);
b(2,:)=w2*a([5:9],:);
b(3,:)=w3*a([10:14],:);
b(4,:)=w4*a([15:end],:)
c=w*b
一级模糊评价后
b =
0.3900 0.3900 0.1700 0.0400 0.0100
0.2500 0.3300 0.2350 0.1250 0.0600
0.1500 0.3200 0.3550 0.1150 0.0600
0.2700 0.3500 0.2600 0.1000 0.0200
二级模糊评价后
c =
0.2880 0.3540 0.2355 0.0865 0.0360
3.数据包络分析

案例:可持续发展
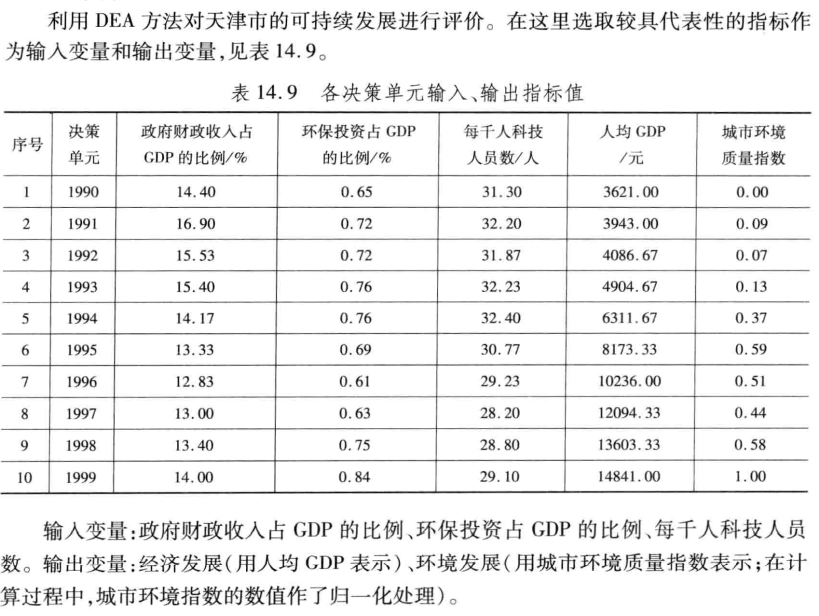
Lingo
model:
sets:
dmu/1..10/:s,t,p; !决策单元,p为单位坐标向量,s,t为中间变量;
inw/1..3/:omega; !输入权重;
outw/1..2/:mu; !输出权重;
inv(inw,dmu):x; !输入变量;
outv(outw,dmu):y;
endsets
data:
ctr=?; !实时输入数据,对第n个单元做评价时,就输入n;
x=14.4 16.9 15.53 15.4 14.17 13.33 12.83 13 13.4 14
0.65 0.72 0.72 0.76 0.76 0.69 0.61 0.63 0.75 0.84
31.3 32.2 31.87 32.23 32.4 30.77 29.23 28.2 28.8 29.1;
y=3621 3943 4086.67 4904.67 6311.67 8173.33 10236 12094.33 13603.33 14841
0 0.09 0.07 0.13 0.37 0.59 0.51 0.44 0.58 1;
enddata
max=@sum(dmu:p*t);
p(ctr)=1;
@for(dmu(i)|i#ne#ctr:p(i)=0);
@for(dmu(j):s(j)=@sum(inw(i):omega(i)*x(i,j));
t(j)=@sum(outw(i):mu(i)*y(i,j));s(j)>t(j));
@sum(dmu:p*s)=1;
end
输入1-10
4.灰色关联分析
【1】流程


【2】案例:供应商


clc, clear
a=[0.83 0.90 0.99 0.92 0.87 0.95
326 295 340 287 310 303
21 38 25 19 27 10
3.2 2.4 2.2 2.0 0.9 1.7
0.20 0.25 0.12 0.33 0.20 0.09
0.15 0.20 0.14 0.09 0.15 0.17
250 180 300 200 150 175
0.23 0.15 0.27 0.30 0.18 0.26
0.87 0.95 0.99 0.89 0.82 0.94];
for i=[1 5:9] %效益型指标标准化
a(i,:)=(a(i,:)-min(a(i,:)))/(max(a(i,:))-min(a(i,:)));
end
for i=2:4 %成本型指标标准化
a(i,:)=(max(a(i,:))-a(i,:))/(max(a(i,:))-min(a(i,:)));
end
[m,n]=size(a);
cankao=max(a')' %求参考序列的取值
t=repmat(cankao,[1,n])-a; %求参考序列与每一个序列的差
mmin=min(min(t)); %计算最小差
mmax=max(max(t)); %计算最大差
rho=0.5; %分辨系数
xishu=(mmin+rho*mmax)./(t+rho*mmax) %计算灰色关联系数
guanliandu=mean(xishu) %取等权重,计算关联度
[gsort,ind]=sort(guanliandu,'descend') %对关联度按照从大到小排序
guanliandu =
0.4630 0.5560 0.6491 0.6527 0.4936 0.6130
ind =
4 3 6 2 5 15.秩和比综合分析

案例:医院质量
clc, clear
aw=load('zhb.txt'); %把x1,...,x6的数据和权重数据保存在纯文本文件zhb.txt中
w=aw(end,:); %提取权重向量
a=aw([1:end-1],:); %提取指标数据
a(:,[2,6])=-a(:,[2,6]); %把成本型指标转换成效益型指标
ra=tiedrank(a) %对每个指标值分别编秩,即对a的每一列分别编秩
[n,m]=size(ra); %计算矩阵sa的维数
RSR=mean(ra,2)/n %计算秩和比
W=repmat(w,[n,1]);
WRSR=sum(ra.*W,2)/n %计算加权秩和比
[sWRSR,ind]=sort(WRSR); %对加权秩和比排序
p=[1:n]/n; %计算累积频率
p(end)=1-1/(4*n) %修正最后一个累积频率,最后一个累积频率按1-1/(4*n)估计
Probit=norminv(p,0,1)+5 %计算标准正态分布的p分位数+5
X=[ones(n,1),Probit']; %构造一元线性回归分析的数据矩阵
[ab,abint,r,rint,stats]=regress(sWRSR,X) %一元线性回归分析
WRSRfit=ab(1)+ab(2)*Probit %计算WRSR的估计值
y=[1983:1992]';
xlswrite('ex147.xls',[y(ind), ra(ind,:), sWRSR],1) %数据写入表单“Sheet1”中
xlswrite('ex147.xls',[y(ind), ones(n,1), [1:n]', p', Probit', WRSRfit', [n:-1:1]'], 2)
%数据写入表单“Sheet2”中 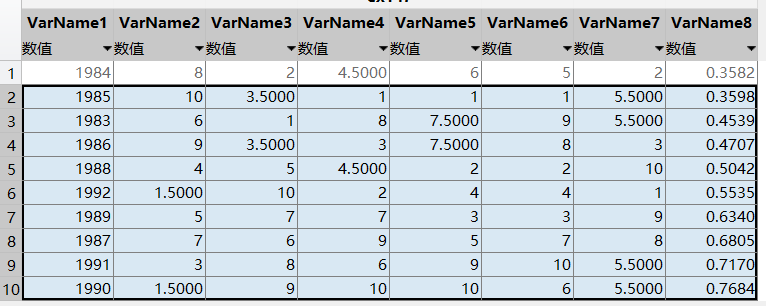
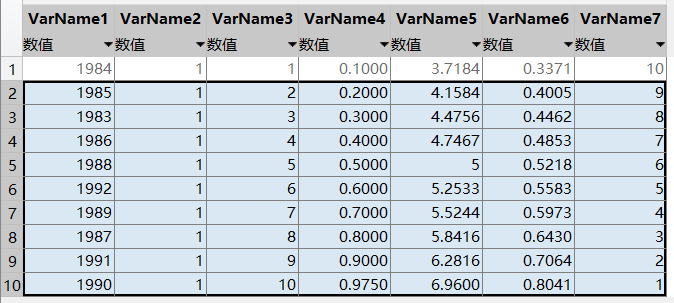
6.熵权法

案例:根据各科成绩排名
clc,clear
a=readmatrix('pjsj.txt');
[n,m]=size(a);
p=a./sum(a);
e=-sum(p.*log(p))/log(n);
g=1-e;w=g/sum(g)
s=w*p'
[ss,ind1]=sort(s,'descend')
ind2(ind1)=1:n7.PageRank算法
已知网络如图,求PagegRank值
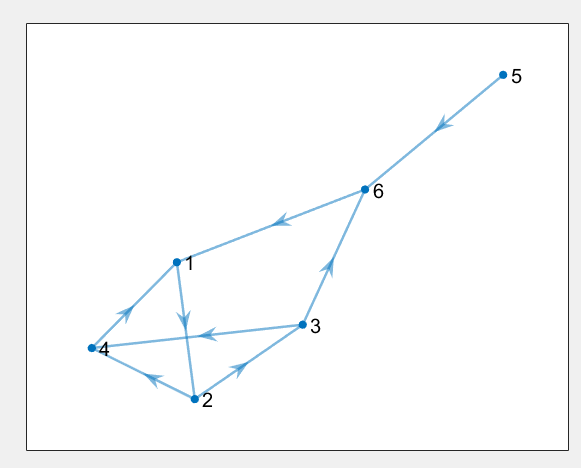
clc,clear,close all
N=6;B=zeros(N);B(1,2)=1;B(2,[3,4])=1;
B(3,[4,6])=1;B(4,1)=1;B(5,6)=1;B(6,1)=1;
nodes={'1','2','3','4','5','6'};
G=digraph(B,nodes);
plot(G,'LineWidth',1.5,'NodeFontSize',12,'ArrowSize',12)
r=sum(B,2);d=0.85;
A=(1-d)/N+d*B./r
[x,y]=eigs(A',1);
x=x/sum(x)
figure,bar(x)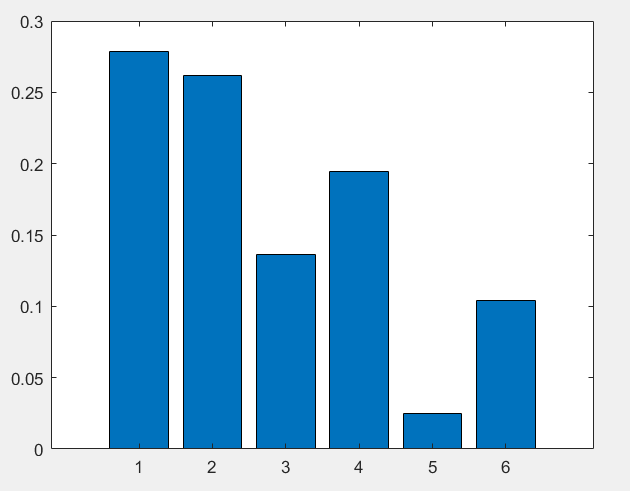























 8308
8308











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










