C++ 数据结构—第一章（要写寄了）

大蒟蒻袁袁

已于 2023-10-20 16:10:06 修改

阅读量247

点赞数 3

分类专栏：蒟蒻讲数据结构文章标签：算法

于 2023-09-30 20:16:49 首次发布

本文链接：https://blog.csdn.net/weixin_66767924/article/details/133433046

版权

蒟蒻讲数据结构专栏收录该内容

4 篇文章 0 订阅

订阅专栏

8.查询最大、最小值（此问题多少有点……为了就是这一步）

（1）对于a[x]+=val;更改树状数组的操作

（2）求区间和（[l,r]的和）

（3）初始化

五、最后

一、二叉搜索树

1.定义

这当然是一个二叉树了。
每个节点的左儿子比自己小。
每个节点的右儿子比自己大。

2.结构代码实现

const int L=0,R=1;//定义常量,防止你写着写着左儿子与右儿子写反了。
struct node{
	int son[2];//记录左右儿子(son[L],son[R],不会写反了吧)。 
	int val;//这个节点储存的值。 
}a[N];
int cnt;

cnt（变量）：用于分配节点编号,a[++cnt](根据个人习惯你怎么用都行,a[cnt++],初始为第一个节点)一个新的节点。

3.二叉搜索树的建立

将节点从根节点开始插入。
与当前节点比较大小。
如果比当前节点存储的值大，向右递归。
如果比当前节点存储的值小，向左递归。

4.最后放图片，这就是二叉搜索树

二、二叉堆

1.定义

二叉堆是一种特殊的二叉树。
满足任意上面节点的值都比下面节点大的叫做大根堆。
满足任意上面节点的值都比下面节点小的叫做小根堆。

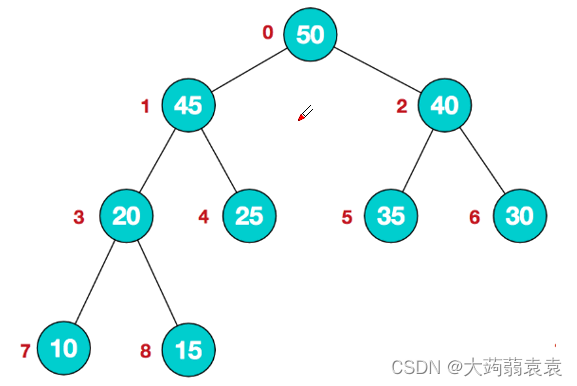
2.大根堆如下

借用一下老师的图片……

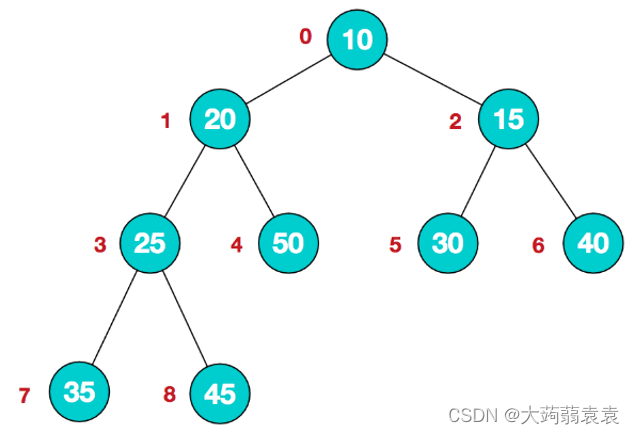
3.小根堆如下

借用一下老师的图片……

4.一般二叉堆能解决什么问题

在 $O(log n)$ 的时间内插入一个元素。
在 $O(log n)$ 的时间内删除一个元素。
在 $O(1)$ 的时间内查询最大、最小值。

5.结构代码实现

节点需要存储左儿子，右儿子，自己的权值，子树大小（唯一跟二叉搜索树不一样的）。

const int L=0,R=1;
struct node{
	int son[2]; 
	int val; 
	int size; 
}a[N];
int cnt;

size（变量）：让堆平衡生长，将新点分到较小的子树，这样100万点差不多就20的深度。有时候随机分配，狠心出题人也没法卡你。

6.插入操作实现（以大根堆为例）

从根节点开始，插入一个值，如果当前值比根节点大，与根节点交换存值。
然后往子树大小更小的儿子递归（平衡生长），直到某个子树大小为0（即没有某一边的儿子），新建一个节点来存储这个值。
这样我们可以保证插入操作一定不超过 $log n$ 次递归。

7.删除操作实现（仍一大根堆为例）

将当前节点权值视为0，与最大的儿子交换权值并递归。
直到节点是一个叶子（无左右儿子），然后删除该叶子（实行上方操作再删）。
这样我们可以保证删除操作一定不超过 $log n$ 次递归。
删除根节点即可弹出最大值。

8.查询最大、最小值（此问题多少有点……为了就是这一步）

取根节点的权值即可。

9.实战

建议实战不要写手写,而使用STL中的priority_queue，万一写wa了那就，欢乐无穷~

三、线段树

1.意义

它是信息学竞赛中特别重要的数据结构，还是信息学奥赛中特别常见的数据结构。

2.线段树能解决什么问题

各种各样的序列操作问题。

例如，有一个长度为N的序列（可能有初始值），然后有Q次操作，每次操作可能是以下两种之一：

修改一个位置的值。
查询一个区间的权值和。
$1\leq N,Q\leq 10^5$

3.线段树的定义

线段树是一种二叉树结构。

线段树上每一个节点对应一个区间 $[L,R]$ 。

节点的左儿子对应 $[L,mid]$ ，右儿子对应 $[mid+1,R]$ 。

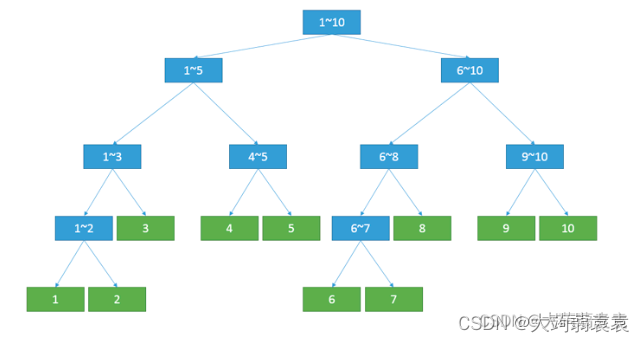
以下就是一个线段树，借用一下老师的图片……

4.结构代码实现

#define N 100005
const int L=0,R=1;
int v[N];//原数组。
struct xds{
    int son[2];//初始化是0。 
    int sum;//区间和。
}a[N*2]; //默认0号点是空,线段树要开N*2(与线段树关联的数组的大小)。 
int cnt;

写拼音虽然很不优雅但是，它不容易重名例如你取一个max的名字直接与max函数重名。

可以不用写管辖区间的L和R，可以用的时候现求。

5.其余代码实现

（1）建树

void build(int &k,int l,int r){//建立线段树, 建立k点，管理区间[l,r]。 
    k=++cnt; // 分出来的第一个数是1。
    if(l==r){
        a[k].sum=v[l]; //初始化信息。
    }else{
        int mid=(l+r)>>1; // 区间中间。 
        build(a[k].son[L],l,mid);//递归建立左儿子， 把 a[k].son[L] 穿进去了，然后这个值递归里会被修改。 
        build(a[k].son[R],mid+1,r);//递归建立右儿子。
        a[k].sum=a[a[k].son[L]].sum+a[a[k].son[R]].sum;//合并左右儿子信息。
    }
}

（2）单点修改操作

void modify(int k,int l,int r,int q,int val){//单点修改操作。
    if(q==l&&r==q){//全区间操作。
        a[k].sum=val;
    }else{
        int mid=(l+r)>>1;
        if(q<=mid) modify(a[k].son[L],l,mid,q,val);
        else if(q>mid) modify(a[k].son[R],mid+1,r,q,val);
        a[k].sum=a[a[k].son[L]].sum+a[a[k].son[R]].sum;//更新自己的区间和。
    }
}

（3）区间查询操作，比如问区间和

int query(int k,int l,int r,int ql,int qr){//区间查询操作，比如问区间和。
    if(ql==l&&r==qr){//全区间查询。
        return a[k].sum;
    }else{
        int mid=(l+r)>>1;
        int ret = 0;
        if(qr<=mid) ret=query(a[k].son[L],l,mid,ql,qr);
        else if(ql>mid) ret=query(a[k].son[R],mid+1,r,ql,qr);
        else ret=query(a[k].son[L],l,mid,ql,mid)+query(a[k].son[R],mid+1,r,mid+1,qr);
        return ret;
    }
}

四、树状数组

1.前置知识：lowbit

lowbit函数是一个常见的位操作函数，用来获取一个整数中最低位的1所对应的值（lowbit函数表示一个整数最大的为2的整次幂的因数）。
$lowbit(x)=(-x )\& x$
$lowbit(x)$ 在下面相当于 $C_x$ 的管辖范围。

2.存储

借用一下老师的图片……

例如 $C_x$ 为 $C_{x+lowbit(x)}$ 的儿子 ,而对于任意一个 $C_x$ 它管理是它的儿子们与 $A_x$ ，可以是它们的和，也可以是其他的。

3.作用

树状数组可以把任意前缀区间拆分成 $log n$ 个已有区间。
所以树状数组可以支持一些单点修改，前缀和查询。
例如修改单点位置的值，求某一个前缀和。

4.代码实现

（1）对于a[x]+=val;更改树状数组的操作

前情提要（2023.10.20增加此解释）：以下代码中x+=low(x)是表示到x的父亲那！

const int N=1000006;//大小。
#define low(x) ((x)&(-(x)))
//lowbit(x)。
int bits[N];//装着每个树状数组节点管理区间的区间和(跟上图的C数组是一个东西)。
void modify(int x,int val){//a[x]+=val;
    for(;x<N;x+=low(x)) bits[x]+=val;//区间和增加val。 
}

（2）求区间和（[l,r]的和）

前情提要（2023.10.20增加此解释）：以下代码中x-=low(x)是表示到前一个兄弟节点那！

int query(int x){// 查询 [1,x] 的和 。
    int ret=0;
    for(;x!=0;x-=low(x))ret+=bits[x];
    return ret;
}

那么接下来就跟前缀和的求法差不多了……

query(R)-query(L-1)

即可求出区间 $[L,R]$ 的和了！

（3）初始化

for(int i=1;i<=n;i++) modify(i, a[i]);// 把初始化变成n次单点修改。

五、最后

第一章终于肝完了~
总结：各有所长，散了吧~

大蒟蒻袁袁

关注

3
点赞
踩
2

收藏

觉得还不错? 一键收藏
1
评论
C++ 数据结构—第一章（要写寄了）

这当然是一个二叉树了。每个节点的左儿子比自己小。每个节点的右儿子比自己大。二叉堆是一种特殊的二叉树。满足任意上面节点的值都比下面节点大的叫做大根堆。满足任意上面节点的值都比下面节点小的叫做小根堆。线段树是一种二叉树结构。线段树上每一个节点对应一个区间。节点的左儿子对应，右儿子对应。以下就是一个线段树，借用一下老师的图片……第一章终于肝完了~总结：各有所长，散了吧
复制链接

扫一扫