操作环境:
MATLAB 2022a
1、算法描述
蚁群算法(Ant Colony Optimization, ACO)是一种启发式优化算法,灵感来源于蚂蚁觅食的自然行为。蚁群算法的核心思想是通过模拟蚂蚁在寻找食物的过程中所形成的集体智能,来解决复杂的组合优化问题。其主要应用于路径规划、网络路由、调度问题等领域。
在自然界中,蚂蚁通过释放一种名为信息素的化学物质来相互传递信息。当一只蚂蚁找到食物源时,它会在返回巢穴的路上沿着所经过的路径释放信息素。其他蚂蚁在寻找食物时,会更倾向于选择信息素浓度较高的路径,这样,经过的信息素越多,路径被蚂蚁选择的概率就越高,从而形成一条优化的路径。通过这个机制,蚁群能够有效地找到食物源,并在一定时间内找到最优的路径。
蚁群算法的基本流程可以分为几个主要步骤。首先,在解决特定问题之前,需要构建一个图模型,将问题转化为图的形式。在这个图中,节点代表问题的状态,边则表示节点之间的连接关系。对于路径规划问题,节点可以表示城市,而边则表示城市之间的距离或权重。接下来,算法会初始化信息素浓度,通常在初始时,所有边的浓度是相同的,代表着对所有路径的均等关注。
然后,算法会进入迭代阶段。在每一轮迭代中,首先会有一群蚂蚁在图上进行移动。蚂蚁的移动是随机的,但也受到信息素浓度的影响。每只蚂蚁在选择下一步移动的节点时,会根据当前节点的邻接节点和它们的信息素浓度来决定。这种选择机制通常采用概率模型,使得信息素浓度高的路径更容易被选择,但仍然保留了一定的随机性,以避免算法陷入局部最优解。
在每次蚂蚁完成一次完整的路径后,算法会根据所找到的路径质量来更新信息素浓度。具体而言,信息素的更新包括两部分:一部分是蒸发,代表信息素随时间的消散,这样可以减少不再被选择的路径的影响;另一部分是强化,即根据蚂蚁所找到路径的质量,增加信息素浓度。路径质量通常通过评价函数来衡量,例如在旅行商问题中,路径的总距离越短,质量越高。
随着迭代次数的增加,信息素的更新逐渐使得路径的选择趋于稳定,最终形成一条最优或接近最优的路径。在这个过程中,蚁群算法充分利用了信息素传递的特点,通过集体合作和信息共享,逐步找到问题的最佳解决方案。
蚁群算法的优点在于其高度的并行性和自适应性。由于每只蚂蚁独立工作,算法能够充分利用计算资源,同时,蚂蚁之间的信息素交互使得算法具有自我调整的能力。此外,蚁群算法对于动态环境的适应能力也相对较强,可以处理问题的变化。
然而,蚁群算法也存在一些局限性。首先,信息素的设置和更新策略对于算法的性能影响较大,选择不当可能导致算法收敛速度慢或陷入局部最优。其次,蚁群算法在处理大规模问题时,计算量会显著增加,因为蚂蚁的数量和迭代次数需要相应增加。此外,算法的参数设置(如信息素蒸发率、蚂蚁数量等)也需要通过实验进行调优,不同问题可能需要不同的参数组合。
为了克服这些问题,研究者们在蚁群算法的基础上提出了多种改进方法。例如,引入遗传算法的思想,通过选择和交叉操作,增强搜索的多样性;或者结合其他优化算法,如粒子群优化,形成混合算法,提高算法的全局搜索能力。这些改进方法使得蚁群算法在处理更加复杂和多变的问题时,能够取得更好的效果。
总之,蚁群算法是一种有效的优化工具,能够在许多复杂问题中找到满意的解决方案。通过模拟自然界中蚂蚁的觅食行为,蚁群算法展现了集体智能的魅力,并为解决实际问题提供了新的思路。随着研究的深入,蚁群算法在理论和应用领域的前景广阔,有望在更多的复杂系统中发挥重要作用。
2、仿真结果演示
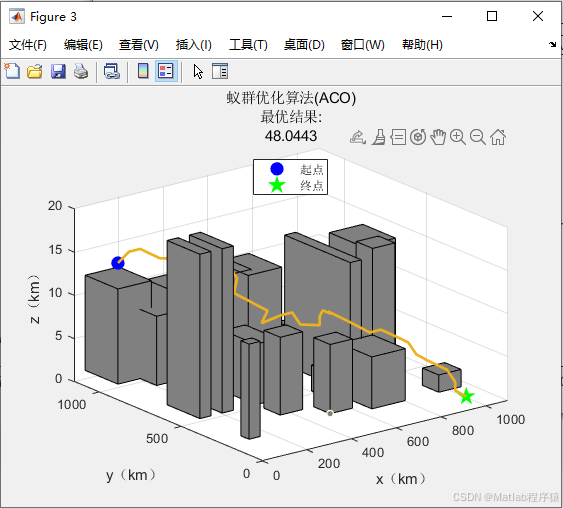

3、关键代码展示
略
4、MATLAB 源码获取
V
点击下方名片关注公众号获取

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








