算法--Union-Find（笔记版）

内容包括：

1.Quick Find

2.Quick Union

3.weighted-Union-Find

4.weighted quick-union with path compression

5.四种的比较

Quick Find

link方式：直接连接，每次连接都更新id[i]

find操作：查看id[p]，id[q]是否相同

#include<iostream>
#include<cmath>

using namespace std;
class UF
{

private:
    int N;
    int *id=new int[N];
public:
    UF(int N)
    {
        this->N=N;
        for (int i = 0; i < N; i++)
        {
            id[i]=i;
            cout<<id[i]<<" ";
        } 
        cout<<endl;
    }
    bool UF_connected(int p,int q)//连接
    {
        return id[p]==id[q];
    }
    void UF_union(int p,int q)//修改连接后的id下标
    {
        int pid=id[p];
        int qid=id[q];
        for (int i = 0; i < N; i++)
        {
            if(id[i]==pid) id[i]=qid;
        }
        
    }
    int Printf_UF()//输出
    {
        for (int i = 0; i < N; i++)
        {
            cout<<id[i]<<" ";
        }
        cout<<endl;
        
    }
    void Destruct_UF()//销毁
    {
        delete[] id;
    }
};
int main()
{
//初始化
    UF uf(6);
//连接0，1；2，4；3，5
    uf.UF_connected(0,1);
    uf.UF_connected(2,4);
    uf.UF_connected(3,5);
    uf.UF_union(0,1);
    uf.UF_union(2,4);
    uf.UF_union(3,5);
    uf.Printf_UF();
//连接1，2
    uf.UF_connected(1,2);
    uf.UF_union(1,2);
    uf.Printf_UF();
    uf.Destruct_UF();
}

构造函数--初始化UF

Quick Union

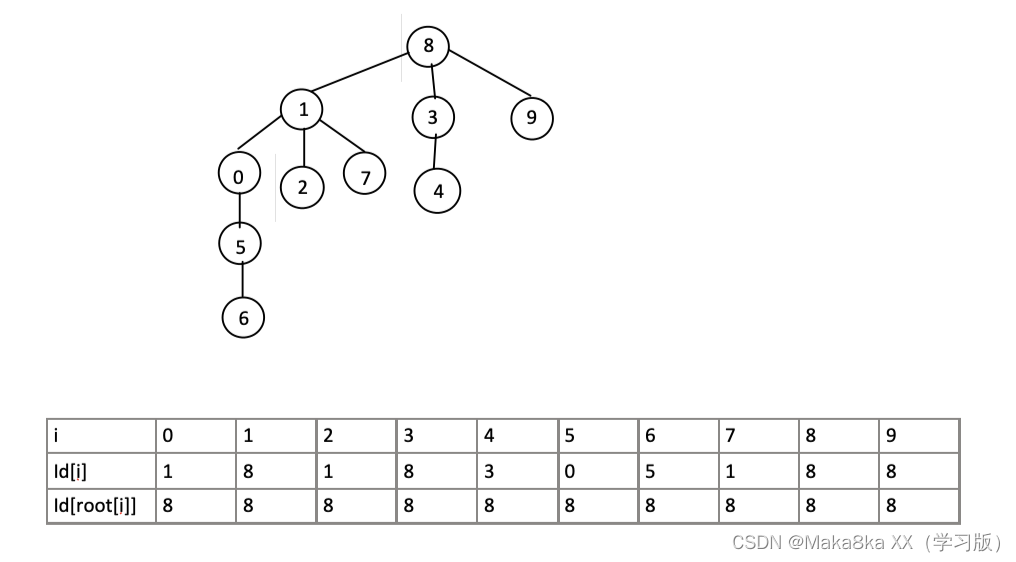
树状：id的值是下标的父元素

连接成树，UF_union(p,q)把前一项根节点作为后一项子节点

i的根节点root是id[id[id[…id[i]…]]]

find操作:p和q是否拥有同一个根节点

相比Quick Find减少连接的时间，如果要把9和6相连，只需要改变id[9]，大大减少了操作时间

//Quick-union
#include<iostream>
#include<cmath>
using namespace std;
class UF
{
private:
    int N;
    int *id=new int[N];
    //私有方法
    int UF_root(int i)//到达根节点，不断向上寻找根id
    {
        while(i!=id[i])
            i=id[i];
        return i;
    }
public:
    UF(int N)//初始化
    {
        this->N=N;
        for (int i = 0; i < N; i++)
        {
            id[i]=i;
            cout<<id[i]<<" ";
        } 
        cout<<endl;
    }
    bool UF_connected(int p,int q)//连接
    {
        return UF_root(p)==UF_root(q);
    }
    void UF_union(int p,int q)//修改连接后的id下标
    {
        int i=UF_root(p);
        int j=UF_root(q);
        id[i]=j;
        
    }
    int Printf_UF()
    {
        for (int i = 0; i < N; i++)//根父元素
        {
            cout<<id[UF_root(i)]<<" ";
        }
        cout<<endl;
        for (int i = 0; i < N; i++)//上一级父元素
        {
            cout<<id[i]<<" ";
        }
        cout<<endl;
        
    }
    void Destruct_UF()
    {
        delete[] id;
    }
};
int main()
{
    UF uf(10);
    uf.UF_connected(4,3);
    uf.UF_connected(3,8);
    uf.UF_connected(6,5);
    uf.UF_connected(9,4);
    uf.UF_connected(2,1);
    uf.UF_connected(5,0);
    uf.UF_connected(7,2);
    uf.UF_connected(6,1);
    uf.UF_connected(7,3);
    uf.UF_union(4,3);
    uf.UF_union(3,8);
    uf.UF_union(6,5);
    uf.UF_union(9,4);
    uf.UF_union(2,1);
    uf.UF_union(5,0);
    uf.UF_union(7,2);
    uf.UF_union(6,1);
    uf.UF_union(7,3);
    uf.Printf_UF();
    uf.Destruct_UF();
}

weighted-Union-Find

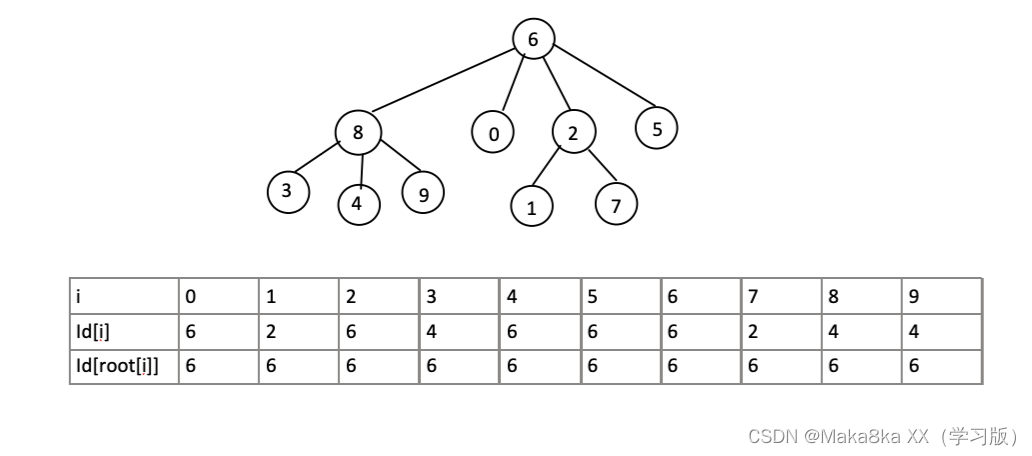
更矮的树：被连接的作为子节点，连接其根节点（改善Quick-Union树太高的问题）

对每个树包含的节点数用sz[]数组记录

union操作：将节点数少的小树的根节点连接到节点数多的大树的根节点上

find操作：时间和p、q的深度成正比

//weighted_Union_Find
//在实现快速联合算法时，避免有高大的树
#include<iostream>
#include<cmath>
using namespace std;
class UF
{
private:
    int N;
    int *id=new int[N];
    int *sz=new int[N];//存放该元素的子元素数量
    //私有方法
    int UF_root(int i)//到达根节点，不断向上寻找根id
    {
        while(i!=id[i])
            i=id[i];
        return i;
    }
public:
    UF(int N)//初始化
    {
        this->N=N;
        for (int i = 0; i < N; i++)
        {
            id[i]=i;
            sz[i]=1;
            cout<<id[i]<<" ";
        } 
        cout<<endl;
    }
    bool UF_connected(int p,int q)//连接
    {
        return UF_root(p)==UF_root(q);
    }
    void UF_union(int p,int q)//修改连接后的id下标
    {
        int i=UF_root(p);
        int j=UF_root(q);
        if (i==j) return;
        if (sz[i]<sz[j])//将小的树连接到大的树上
        {
            id[i]=j;
            sz[j]+=sz[i];
        }
        else
        {
            id[j]=i;
            sz[i]+=sz[j];
        }
                
        
    }
    int Printf_UF()
    {
        for (int i = 0; i < N; i++)//根父元素
        {
            cout<<id[UF_root(i)]<<" ";
        }
        cout<<endl;
        for (int i = 0; i < N; i++)//上一级父元素
        {
            cout<<id[i]<<" ";
        }
        cout<<endl;
    }
    void Destruct_UF()
    {
        delete[] id;
    }
};
int main()
{
    UF uf(10);
    uf.UF_connected(4,3);
    uf.UF_connected(3,8);
    uf.UF_connected(6,5);
    uf.UF_connected(9,4);
    uf.UF_connected(2,1);
    uf.UF_connected(5,0);
    uf.UF_connected(7,2);
    uf.UF_connected(6,1);
    uf.UF_connected(7,3);
    uf.UF_union(4,3);
    uf.UF_union(3,8);
    uf.UF_union(6,5);
    uf.UF_union(9,4);
    uf.UF_union(2,1);
    uf.UF_union(5,0);
    uf.UF_union(7,2);
    uf.UF_union(6,1);
    uf.UF_union(7,3);
    uf.Printf_UF();
    uf.Destruct_UF();
}

weighted quick-union with path compression

压扁的树（路径压缩）：​​​​​​​每次都更新元素的父元素为当前最高层父元素

//weighted quick-union with path compression
//压扁树
#include<iostream>
#include<cmath>
using namespace std;
class UF
{
private:
    int N;
    int *id=new int[N];
    int *sz=new int[N];//存放该元素的子元素数量
    //私有方法
    int UF_root(int i)//每次都更新元素的父元素为当前最高层父元素
    {
        while(i!=id[i])
        {
            id[i]=id[id[i]];
            i=id[i];
        }
        return i;
    }
public:
    UF(int N)//初始化
    {
        this->N=N;
        for (int i = 0; i < N; i++)
        {
            id[i]=i;
            sz[i]=1;
            cout<<id[i]<<" ";
        } 
        cout<<endl;
    }
    bool UF_connected(int p,int q)//连接
    {
        return UF_root(p)==UF_root(q);
    }
    void UF_union(int p,int q)//修改连接后的id下标
    {
        int i=UF_root(p);
        int j=UF_root(q);
        if (i==j) return;
        if (sz[i]<sz[j])//将小的树连接到大的树上
        {
            id[i]=j;
            sz[j]+=sz[i];
        }
        else
        {
            id[j]=i;
            sz[i]+=sz[j];
        }
                
        
    }
    int Printf_UF()
    {
        for (int i = 0; i < N; i++)//根父元素
        {
            cout<<id[UF_root(i)]<<" ";
        }
        cout<<endl;
        for (int i = 0; i < N; i++)//上一级父元素
        {
            cout<<id[i]<<" ";
        }
        cout<<endl;
    }
    void Destruct_UF()
    {
        delete[] id;
    }
};
int main()
{
    UF uf(10);
    uf.UF_connected(4,3);
    uf.UF_connected(3,8);
    uf.UF_connected(6,5);
    uf.UF_connected(9,4);
    uf.UF_connected(2,1);
    uf.UF_connected(5,0);
    uf.UF_connected(7,2);
    uf.UF_connected(6,1);
    uf.UF_connected(7,3);
    uf.UF_union(4,3);
    uf.UF_union(3,8);
    uf.UF_union(6,5);
    uf.UF_union(9,4);
    uf.UF_union(2,1);
    uf.UF_union(5,0);
    uf.UF_union(7,2);
    uf.UF_union(6,1);
    uf.UF_union(7,3);
    uf.Printf_UF();
    uf.Destruct_UF();
}

操作时间复杂度比较

*表示最大次数