题目概况:
输入两个数 a、b,求这两个数的最大公因数
解题思路:

如果b等于0的话,计算结束,a就是最大公因数
如果b不等于0,那么就去计算 a 对 b 的余数 r ,之后将 a 取 b 的值,b 取 r 的值,再回到第一步直到b为0为止。
以 a=12,b=18 为例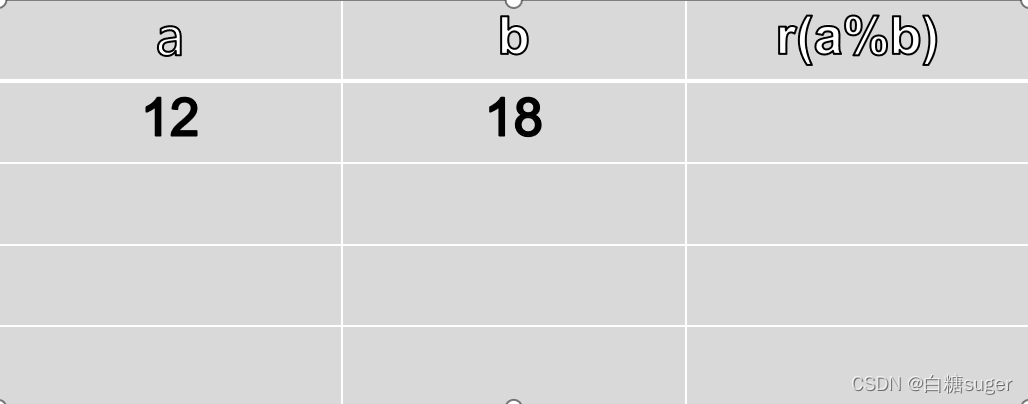
接下来求 a 对 b 的余数 r ;并且将 b 的值赋予a,r 的值赋予 b ;
在重复上述过程,直到b的值是0;
综合图解,是可以看出是有规律可循的,表格中的值每一个值是自右向左依次传递的 ,a的值是右边的b传递的,b的值又是其右边的r传递的 ,r的值是a与b相除取余得到的,所以叫辗转相除法
代码演示:
int main(){
int a,b;
scanf("%d",&a);
scanf("%d",&b);
while(b!=0){
int r=a%b;
a=b;
b=r;
}
printf("最大公因数是:%d",a);
return 0;
}







 本文介绍了如何利用辗转相除法(欧几里得算法)求解两个整数的最大公因数(GCD)。通过示例12和18,详细解释了算法的步骤:当b不等于0时,计算a对b的余数r,然后a取b的值,b取r的值,如此迭代直至b为0,最后的a即为最大公因数。提供的C语言代码展示了这一过程。
本文介绍了如何利用辗转相除法(欧几里得算法)求解两个整数的最大公因数(GCD)。通过示例12和18,详细解释了算法的步骤:当b不等于0时,计算a对b的余数r,然后a取b的值,b取r的值,如此迭代直至b为0,最后的a即为最大公因数。提供的C语言代码展示了这一过程。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








