一、基础:石子合并
链接:登录—专业IT笔试面试备考平台_牛客网
设有N堆沙子排成一排,其编号为1,2,3,…,N1,2,3,\dots ,N1,2,3,…,N(N≤300)(N\leq 300)(N≤300)。每堆沙子有一定的数量,可以用一个整数来描述,现在要将这N堆沙子合并成为一堆,每次只能合并相邻的两堆,合并的代价为这两堆沙子的数量之和,合并后与这两堆沙子相邻的沙子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同,如有4堆沙子分别为 1 3 5 2 我们可以先合并1、2堆,代价为4,得到4 5 2 又合并 1,2堆,代价为9,得到9 2 ,再合并得到11,总代价为4+9+11=24,如果第二步是先合并2,3堆,则代价为7,得到4 7,最后一次合并代价为11,总代价为4+7+11=22;问题是:找出一种合理的方法,使总的代价最小。输出最小代价。
解题
dp思路如下:
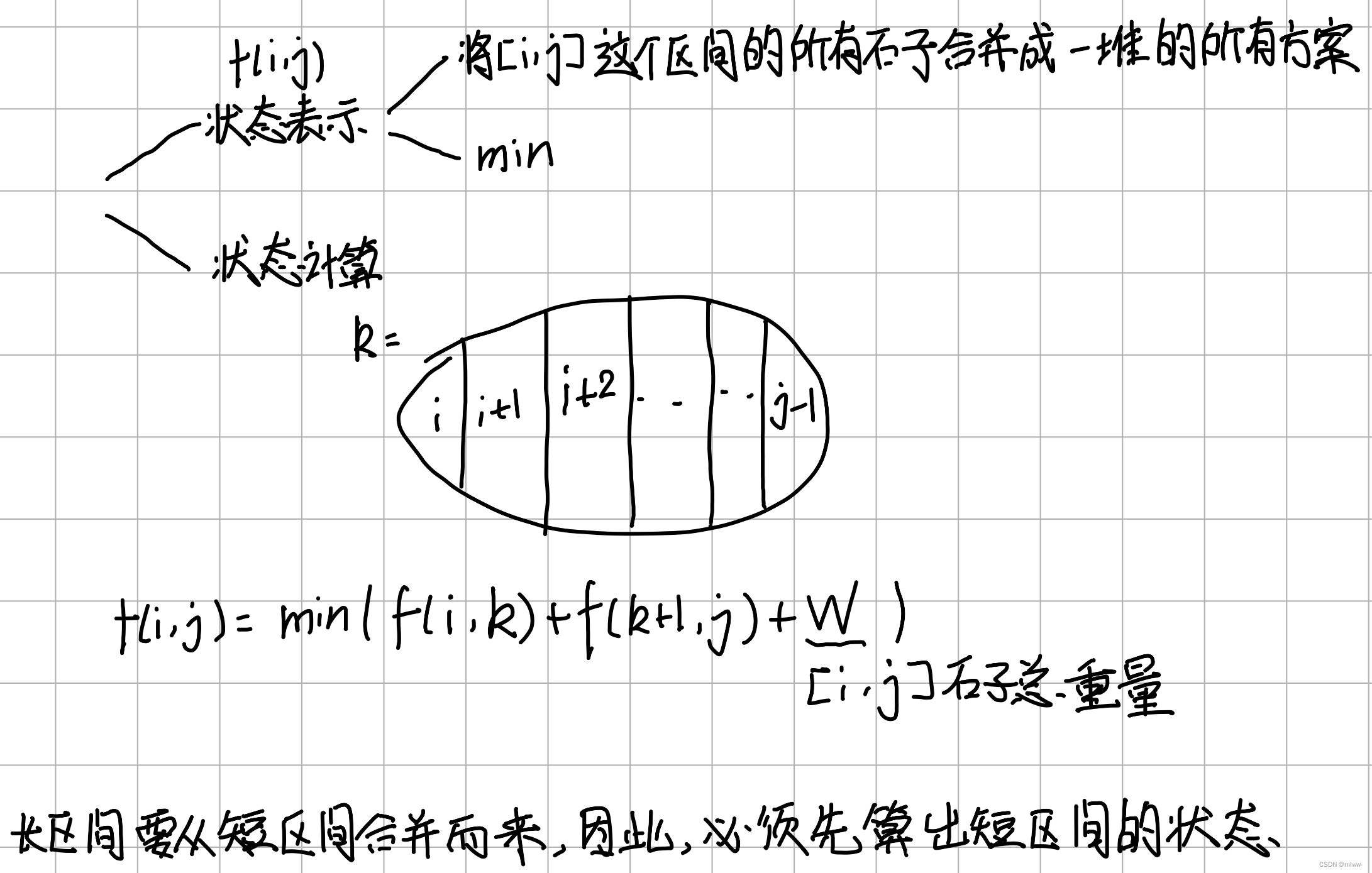
在计算[i,j]区间的石子总重量时,可以用前缀和。
还需要注意的是我们在进行状态转移时,顺序应该是先枚举短区间,再枚举长区间,因此for循环的内容是区间长度和起点。
#include<iostream>
using namespace std;
const int N=310;
int n,w[N];
int f[N][N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&w[i]);
w[i]+=w[i-1];
}
for(int len=2;len<=n;len++)
{
for(int i=1;i+len-1<=n;i++)
{
int l=i,r=i+len-1;
f[l][r]=1e9;
for(int k=l;k<r;k++)
{
f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+w[r]-w[l-1]);
}
}
}
printf("%d",f[1][n]);
}二、环形区间dp
题目1:环形石子合并
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
将n堆石子绕圆形操场排放,现要将石子有序地合并成一堆。规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数n及每堆的石子数,并进行如下计算:
- 选择一种合并石子的方案,使得做n-1次合并得分总和最大。
- 选择一种合并石子的方案,使得做n-1次合并得分总和最小。
解题
对于处理环形问题,通用的方案是开两倍区间,将a数组的[1,n]复制一遍到[n+1,2n],在[1,2n]范围内寻找长度为n的区间,就能够实现环形的效果。
#include<iostream>
using namespace std;
const int N=210;
int n,a[N],s[N*2];
int f1[N*2][N*2],f2[N*2][N*2];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
s[i]=s[i-1]+a[i];
}
for(int i=n+1;i<=2*n;i++) s[i]=a[i-n]+s[i-1];
for(int len=2;len<=n;len++)
for(int i=1;i+len-1<=2*n;i++)
{
int l=i,r=i+len-1;
f1[l][r]=1e9;
f2[l][r]=-1e9;
for(int k=l;k<r;k++)
{
f1[l][r]=min(f1[l][r],f1[l][k]+f1[k+1][r]+s[r]-s[l-1]);
f2[l][r]=max(f2[l][r],f2[l][k]+f2[k+1][r]+s[r]-s[l-1]);
}
}
int res1=1e9,res2=-1e9;
for(int i=1;i+n-1<=2*n;i++)
{
int l=i,r=i+n-1;
res1=min(res1,f1[l][r]);
res2=max(res2,f2[l][r]);
}
printf("%d\n%d",res1,res2);
}
题目2:能量项链
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链,在项链上有N颗能量珠。
能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。
并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样,通过吸盘(吸盘是 Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。
如果前一颗能量珠的头标记为m,尾标记为r,后一颗能量珠的头标记为r,尾标记为n,则聚合后释放的能量为m×r×n(Mars 单位),新产生的珠子的头标记为m,尾标记为n。
需要时,Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
解题
我们先从链的情况考虑,2 3 5 10的序列,实际上表示的是(2*3)(3*5)(5*10)(10*2)四颗石头,其实是2 3 5 10 2这个序列,前面就可以用和石子合并相同的方式进行状态表示和状态计算。
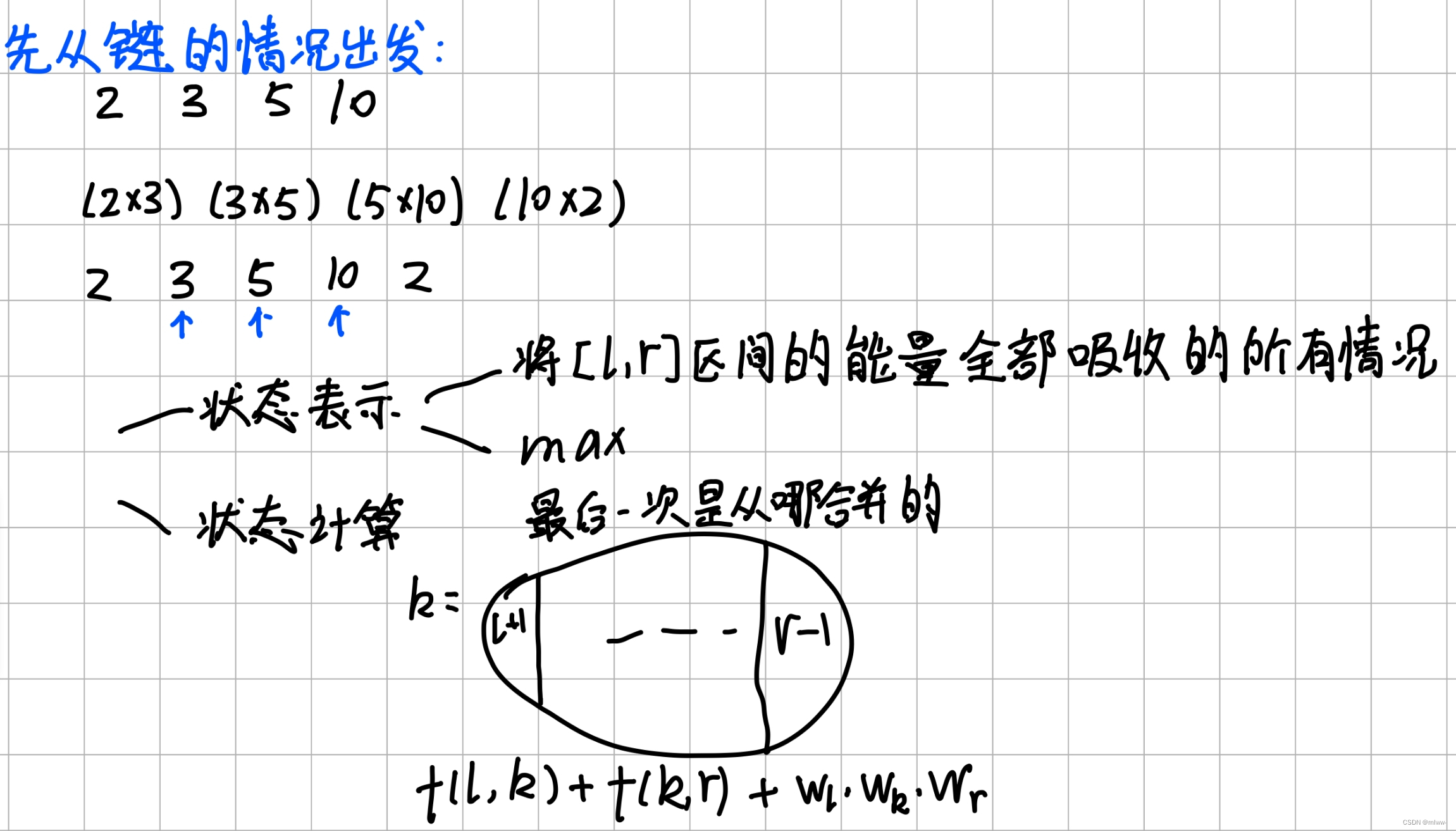
接下来,我们就可以把数组开成2维,用环形区间的通用做法来做。
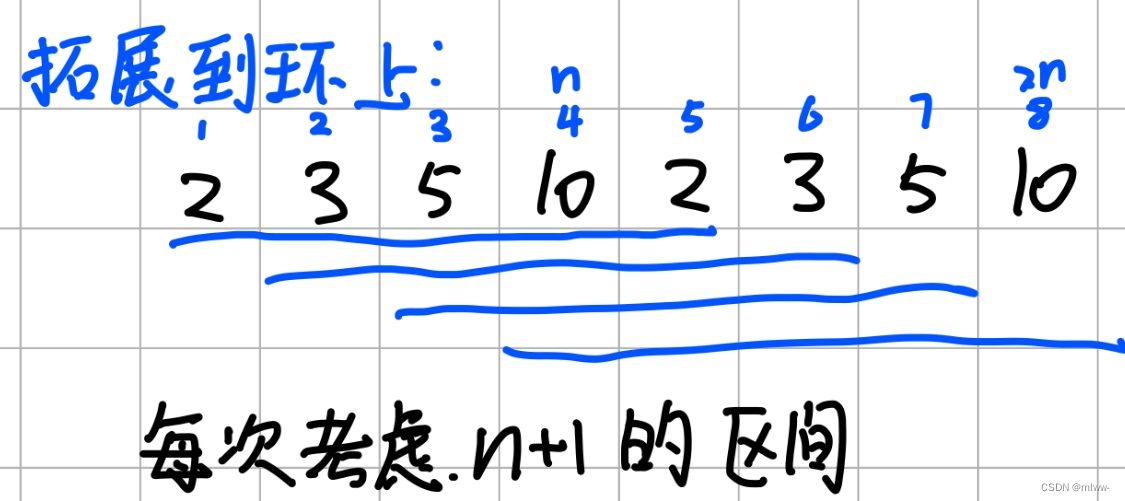
和环形石子合并不同的是,在环形石子合并过程中,我们枚举的合并点是两堆石子中间的点;而在能量项链问题中,我们进行合并的点应该是某一个数字所处的位置,当len=2,i=1时,我们其实就是将(2*3)和(5*10)两块石头合并,因此,在这个问题中,r=l+len而不是l+len-1了。
或者可以直接让len从3开始枚举。

#include<iostream>
using namespace std;
const int N=110;
int n,a[N*2];
int f[2*N][2*N];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=n+1;i<=2*n;i++) a[i]=a[i-n];
for(int len=2;len<=n+1;len++)
{
for(int i=1;i+len<=2*n;i++)
{
int l=i,r=i+len;
f[l][r]=-2e9-1e8;
for(int k=l+1;k<r;k++)
{
f[l][r]=max(f[l][r],f[l][k]+f[k][r]+a[l]*a[k]*a[r]);
}
}
}
int res=-2e9-1e8;
for(int i=1;i<=n;i++) res=max(res,f[i][i+n]);
printf("%d",res);
}题目3:凸多边形的划分
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
给定一个具有N个顶点的凸多边形,将顶点从1至N标号,每个顶点的权值都是一个正整数。将这个凸多边形划分成N-2个互不相交的三角形,试求这些三角形顶点的权值乘积和至少为多少。
解题
这题的难点在于如何把它与区间dp联系起来。
先把样例画出来。
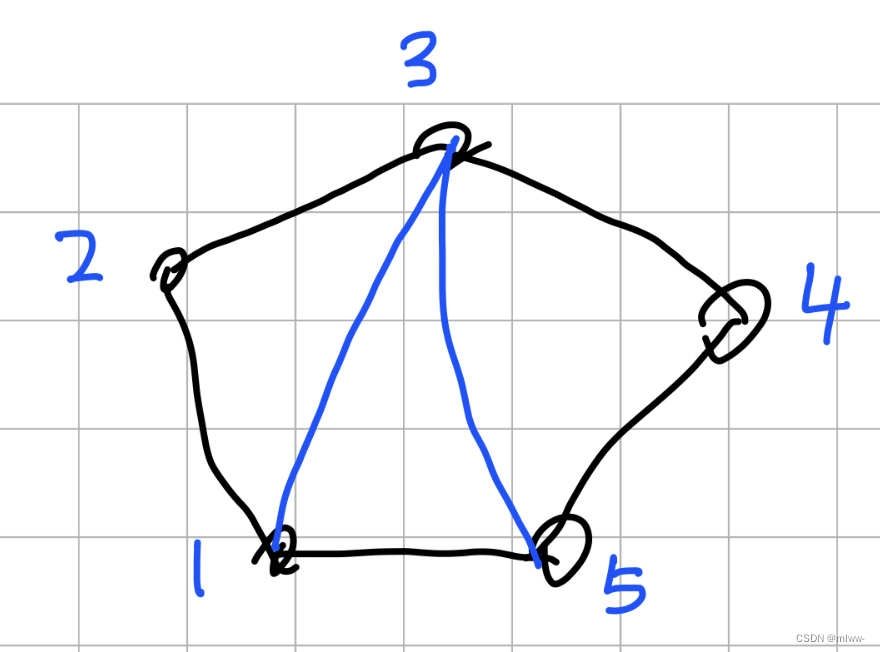
可以发现,在多边形中,只要我们确定了一个顶点和一条底边,就能构造出一个三角形,这个三角形会把大多边形分成三个部分:左边、右边和三角形本身。这就是我们进行状态转移的依据。dp思路如下:
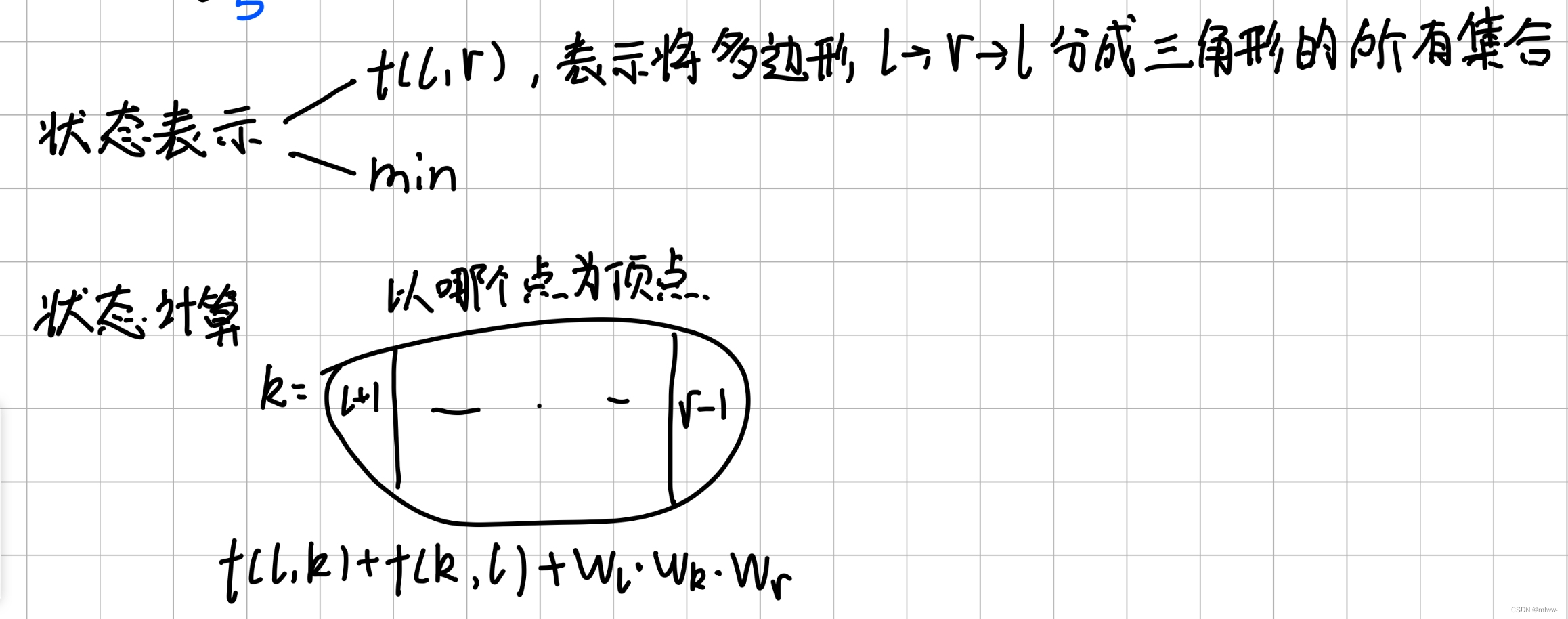
除了思路上的问题,在实现时,因为顶点权值的范围是0-1e9,这题涉及到高精度计算。由于需要将dp数组初始化为正无穷,用vector难以实现高精度,要用数组来实现,多了很多细节。
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=55,M=35;
int n,a[N];
ll f[N][N][M];
void add(ll a[],ll b[])
{
static ll c[M];
memset(c,0,sizeof(c));
ll t=0;
for(int i=0;i<M;i++)
{
t+=a[i]+b[i];
c[i]=t%10;
t/=10;
}
memcpy(a,c,sizeof(c));
}
void mul(ll a[],ll b)
{
static ll c[M];
memset(c,0,sizeof(c));
ll t=0;
for(int i=0;i<M;i++)
{
t+=a[i]*b;
c[i]=t%10;
t/=10;
}
memcpy(a,c,sizeof(c));
}
bool cmp(ll a[],ll b[])
{
static ll c[M];
for(int i=M-1;i>=0;i--)
{
if(a[i]>b[i]) return 1;
else if(a[i]<b[i]) return 0;
}
return 0;
}
void print(ll a[])
{
int k=M-1;
while(k>=0&&a[k]==0) k--;
while(k>=0) printf("%lld",a[k--]);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int len=2;len<=n;len++)
for(int i=1;i+len<=n;i++)
{
int l=i,r=i+len;
f[l][r][M-1]=1;
for(int k=l+1;k<r;k++)
{
ll temp[M];
memset(temp,0,sizeof(temp));
temp[0]=a[l];
mul(temp,a[k]);
mul(temp,a[r]);
add(temp,f[l][k]);
add(temp,f[k][r]);
if(cmp(f[l][r],temp)) memcpy(f[l][r],temp,sizeof(temp));
}
}
print(f[1][n]);
}三、区间dp求方案
题目1:加分二叉树
设一个n个节点的二叉树 tree 的中序遍历为(1,2,3,…,n),其中数字 1,2,3,…,n为节点编号。
每个节点都有一个分数(均为正整数),记第 i� 个节点的分数为 di��,tree 及它的每个子树都有一个加分,任一棵子树 subtree(也包含 tree 本身)的加分计算方法如下:
subtree的左子树的加分 × subtree的右子树的加分 + subtree的根的分数
若某个子树为空,规定其加分为 1。
叶子的加分就是叶节点本身的分数,不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树 tree。
解题
这道题的dp思路很常规,如下:
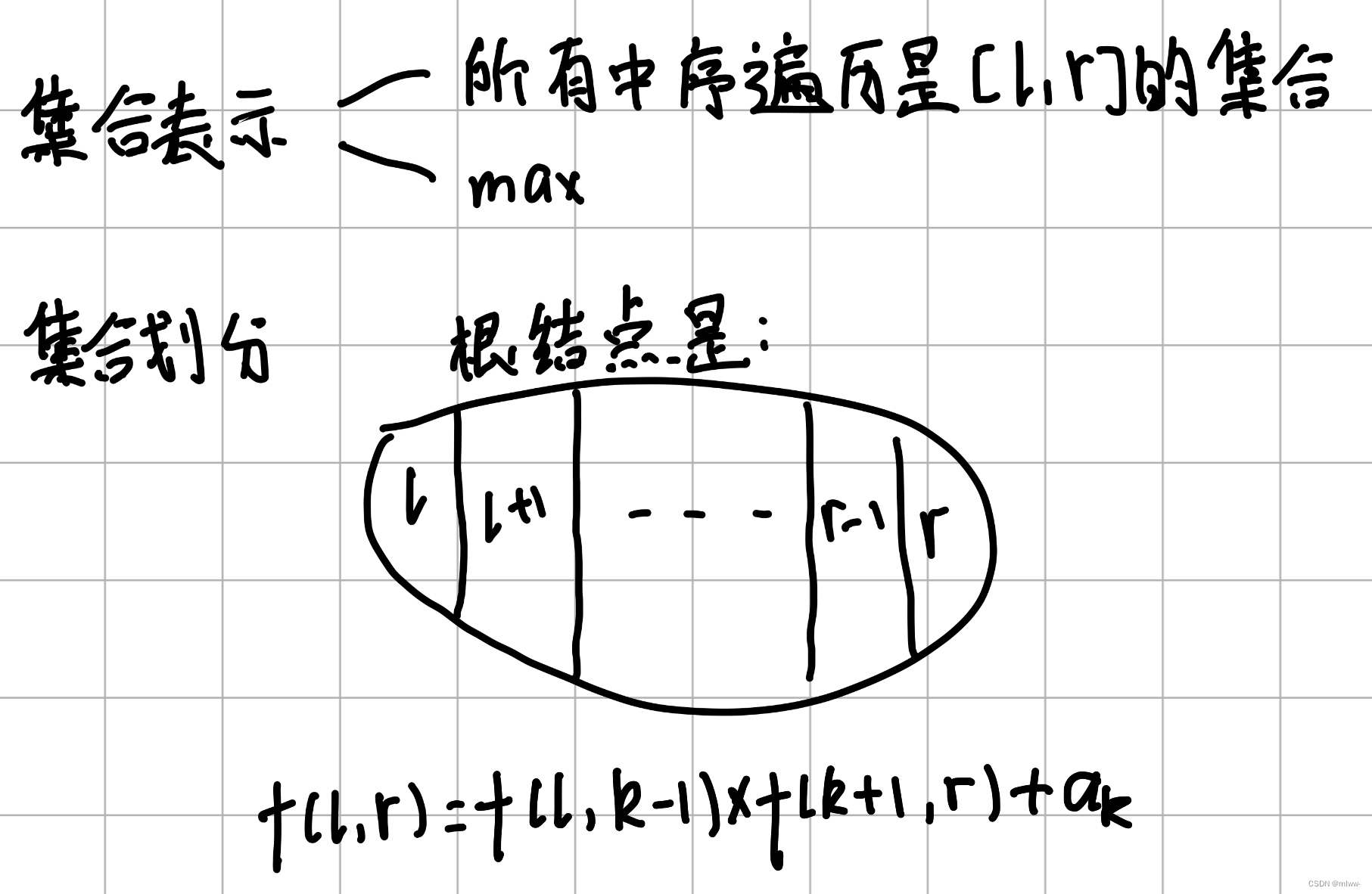
变式的地方在于题目需要求一个方案数。在这道题中,我们通过不同的根节点来划分状态,可以通过额外开一个数组,记录区间[l,r]内最大分数树的根节点,然后通过前序遍历,递归还原方案。
#include<iostream>
#include<cstring>
using namespace std;
const int N=35;
int n,a[N];
int f[N][N];
int g[N][N];
void dfs(int l,int r)
{
int u=g[l][r];
if(u==0) return;
printf("%d ",u);
dfs(l,u-1);
dfs(u+1,r);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int len=1;len<=n;len++)
for(int i=1;i+len-1<=n;i++)
{
int l=i,r=i+len-1;
if(len==1)
{
f[l][r]=a[l];
g[l][r]=l;
}
else
for(int k=l;k<=r;k++)
{
int left=k==l?1:f[l][k-1];
int right=k==r?1:f[k+1][r];
int score=left*right+a[k];
if(f[l][r]<score)
{
f[l][r]=score;
g[l][r]=k;
}
}
}
printf("%d\n",f[1][n]);
dfs(1,n);
}四、二维区间dp
题目1:棋盘分割
解题
在每一次切割后,矩形会被分成两个部分,舍弃部分和继续切割的部分。我们可以选择在1-7的框线上横切或者竖切,每次切割可以在两块矩形中选择保留一块。
dp思路如下:
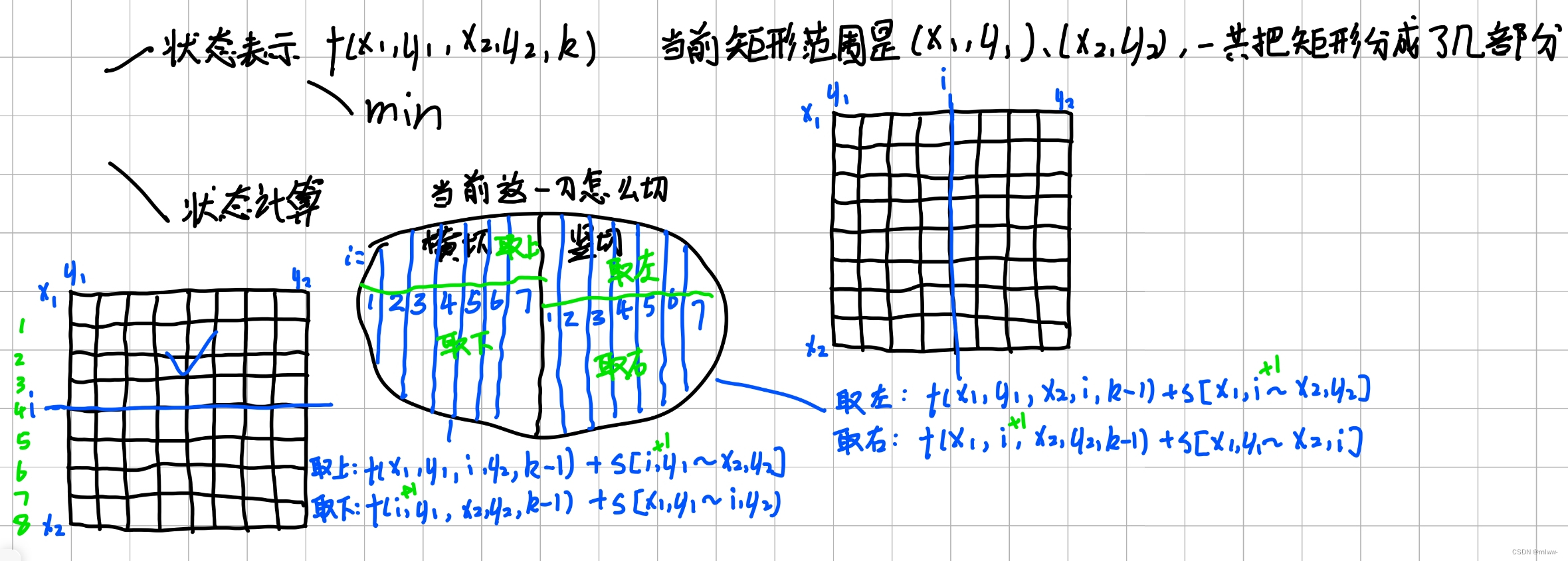
记忆化搜索写法:
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
const int N=10,M=20;
const double INF=1e9;
int n,s[N][N];
double f[N][N][N][N][M];
double X;
double get(int x1,int y1,int x2,int y2)
{
double sum=s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]-X;
return sum*sum/n;
}
double dp(int x1,int y1,int x2,int y2,int k)
{
double &v=f[x1][y1][x2][y2][k];
if(v>=0) return v;
if(k==1) return v=get(x1,y1,x2,y2);
v=INF;
for(int i=x1;i<x2;i++)
{
v=min(dp(x1,y1,i,y2,k-1)+get(i+1,y1,x2,y2),v);
v=min(dp(i+1,y1,x2,y2,k-1)+get(x1,y1,i,y2),v);
}
for(int i=y1;i<y2;i++)
{
v=min(dp(x1,y1,x2,i,k-1)+get(x1,i+1,x2,y2),v);
v=min(dp(x1,i+1,x2,y2,k-1)+get(x1,y1,x2,i),v);
}
return v;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=8;i++)
for(int j=1;j<=8;j++)
{
scanf("%d",&s[i][j]);
s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
}
X=(double)s[8][8]/n;
memset(f,-1,sizeof(f));
printf("%.3lf",sqrt(dp(1,1,8,8,n)));
}数组写法:
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
const int N=10,M=20;
const double INF=1e9;
int n,s[N][N];
double f[N][N][N][N][M];
double X;
double get(int x1,int y1,int x2,int y2)
{
double sum=s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]-X;
return sum*sum/n;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=8;i++)
for(int j=1;j<=8;j++)
{
scanf("%d",&s[i][j]);
s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
}
X=(double)s[8][8]/n;
for(int len1=1;len1<=8;len1++)
for(int l1=1;l1+len1-1<=8;l1++)
for(int len2=1;len2<=8;len2++)
for(int l2=1;l2+len2-1<=8;l2++)
{
int x1=l1,x2=l1+len1-1,y1=l2,y2=l2+len2-1;
for(int k=1;k<=n;k++)
{
if(k==1) f[x1][y1][x2][y2][k]=get(x1,y1,x2,y2);
else
{
f[x1][y1][x2][y2][k]=INF;
for(int i=x1;i<x2;i++)
{
f[x1][y1][x2][y2][k]=min(f[x1][y1][i][y2][k-1]+get(i+1,y1,x2,y2),f[x1][y1][x2][y2][k]);
f[x1][y1][x2][y2][k]=min(f[i+1][y1][x2][y2][k-1]+get(x1,y1,i,y2),f[x1][y1][x2][y2][k]);
}
for(int i=y1;i<y2;i++)
{
f[x1][y1][x2][y2][k]=min(f[x1][y1][x2][i][k-1]+get(x1,i+1,x2,y2),f[x1][y1][x2][y2][k]);
f[x1][y1][x2][y2][k]=min(f[x1][i+1][x2][y2][k-1]+get(x1,y1,x2,i),f[x1][y1][x2][y2][k]);
}
}
}
}
printf("%.3lf",sqrt(f[1][1][8][8][n]));
}




















 2352
2352











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








