求最大公约数 欧几里得算法(辗转相除法)

求最大公约数的常见方法

1. 短除法

1.什么是短除法?
例如:求 18 和 24 的最大公约数

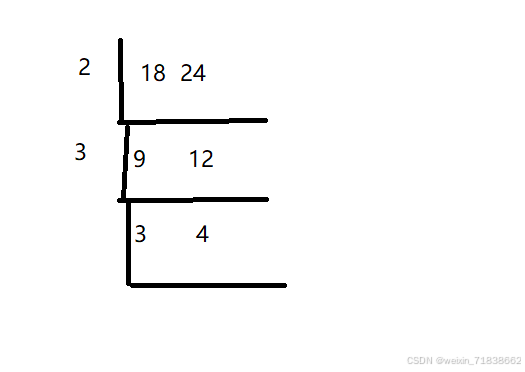
18 和 24 的最大公约数 就为 2 * 3 = 6.

int main()
{
	int num1 = 0;
	int num2 = 0;
	int i = 0;
	int res = 1;
	scanf("%d%d", &num1, &num2);
	if (num2 > num1)//求两个数较小的,以便于后续确定控制语句的范围
	{
		int tmp = num1;
		num1 = num2;
		num2 = tmp;
	}
	for (i = 2; i <= num2; i++)
	{
		while ((num1 % i == 0) && (num2 % i == 0))
		{
			res *= i;
			num1 /= i;
			num2 /= i;
		}
	}
	printf("最大公约数为:%d\n", res);

	return 0;
}

上面的求两个数较小的数也可以这样做
int mul_num = num1 > num2 ? num2:num1;

2.欧几里得算法(最常用的方法)

1. 相比于短除法 当数字很大的时候,短除法就显得不那么容易了,那么我们现在了解一下欧几里得算法.
   首先,我们先了解一些图形,来更加容易我们了解欧几里得算法
   例如:我们现在来求18和24的最大公约数.
   我们现在先画一个矩形 长为 24 宽为 18
   

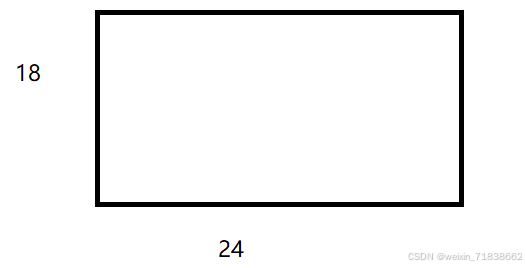
那么我们现在需要将 18 的正方形放里面

同理 将较小的边长6 继续放在18* 24 里面 我们将得到

最后我们得到了一个填充完毕的图,最后填充完毕的图边长是多少,既公约数就是多少所以 18 和 24 的最大公约数就是6

2. 欧几里得算法表示方法:
   ① 用被除数 除以 除数 得到 商 和 余数
   ② 将得到的 除数作为被除数 余数除数
   ③ 重复以上 直到余数为0,除数就是我们的最大公约数
   eg:
   24 / 18 = 1 …6
   18 / 6 = 3 … 0
   即 6 是 24 和 18 的最大公约数

首先 对于任何一个数 我们可以写成
A = B * q + p
由此我们得到的结论为: (A,B) = (B ,P) 既A,B的最大公约数 和 B,P的最大公约数相同.
证明 :①首先我们假设 A,B的最大公约数为 u
②既 A = a *u B = b *u
③ 那我们由上面公式可以写成 : p = A - B ✖ q
代换 得 p = a✖u - (b✖u)✖q
将u 提出来 p = u(a - b✖q)
因为 a b q 都是整数 则 (a - b ✖q)都是整数,所以 p = u✖n,n就是(a-b✖q)
既 p = un
所以 (A,B) = (B,P);

int main()
{
	int num1 = 0;
	int num2 = 0;
	scanf("%d%d", &num1, &num2);
	if (num2 > num1)
	{
		int tmp = num1;
		num1 = num2;
		num2 = tmp;
	}
	while (num1 % num2 != 0)
	{
		int tmp = 0;
		tmp = num1;
		num1 = num2;
		num2 = tmp % num2;
	}
	printf("最大公约数为 : %d", num2);
}