【数学建模学习手册】第一章：解析方法与几何模型（一）

本专栏内容为：数学建模原理 记录学习数学建模

💓博主csdn个人主页：小小unicorn
⏩专栏分类：数学建模
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

前言

今天，人类社会正处在由工业化社会向信息化社会过渡的变革。以数字化为特征的信息社会有两个显著特点：计算机技术的迅速发展与广泛应用；数学的应用向一切领域渗透。随着计算机技术的飞速发展，科计算的作用越来越引起人们的广泛重视，它已经与科学理论和科学实验并列成为人们探索和研究自然界、人类社会的三大基本方法。为了适应这种社会的变革， 培养和造就出一批又一批适应高度信息化社会具有创新能力的高素质的工程技术和管理人才，在各高校开设“数学建模”课程，培养学生的科学计算能力和创新能力，就成为这种新形势下的历史必然。

数学建模是对现实世界的特定对象，为了特定的目的，根据特有的内在规律，对其进行必要的抽象、归纳、假设和简化，运用适当的数学工具建立的一个数学结构。数学建模就是运用数学的思想方法、数学的语言去近似地刻画一个实际研究对象，构建一座沟通现实世界与数学世界的桥梁， 并以计算机为工具应用现代计算技术达到解决各种实际问题的目的。建立一个数学模型的全过程称为数学建模。因此“数学建模”（或数学实验）课程教学对于开发学生的创新意识，提升人的数学素养，培养学生创造性地应用
数学工具解决实际问题的能力，有着独特的功能。

数学建模过程就是一个创造性的工作过程。 人的创新能力首先是创造性思维和具备创新的思想方法。数学本身是一门理性思维科学，数学教学正是通过各个教学环节对学生进行严格的科学思维方法的训练，从而引发人的灵感思维，达到培养学生的创造性思维的能力。同时数学又是一门实用科学，它具有能直接用于生产和实践，解决工程实际中提出的问题，推动生产力的发展和科学技术的进步。

学生通过参加数学建模活动，首先就要了解问题的实际背景，深入到具体学科领域的前沿，这就需要学生具有能迅速查阅大量科学资料，准确获得自己所需信息的能力；同时，不但要求学生必需了解现代数学各
门学科知识和各种数学方法，把所掌握的数学工具创造性地应用于具体的实际问题，构建其数学结构，还要求学生熟悉各种数学软件，熟练地把现代计算机技术应用于解决当前实际问题综合能力，最后还要具有把自己的实践过程和结果叙述成文字的写作能力。通过数学建模全过程的各个环节，学生们进行着创造性的思维活动，模拟了现代科学研究过程。通过“数学建模”课程的教学和数学建模活动极大地开发了学生的创造性思维
的能力，培养学生在面对错综复杂的实际问题时，具有敏锐的观察力和洞察力，以及丰富的想象力。

向量表示法

分析几何问题，在现在这个阶段我们所掌握的方法大体上可以分为三种：

传统几何的演绎-证明体系：

这种体系下的方法都是基于已经被证明了的公理与定理体系（例如勾股定理、正弦定理、圆幂定理等），在解决问题的过程中更强调分析而非计算，往往是通过构造辅助线、辅助平面等利用严密的逻辑推理步步为营推导出最后的结果。这种方法往往分析起来会更加困难，但减少了计算量。

基于向量的计算化几何：

向量被引入几何当中最初的目的是为了表示有向线段，但后来大家发现基于向量的一些运算特性可以把一些数量问题统一化。几何图形中的边长、角度、面积可以转化为向量的模长、内积等求解，平行、垂直等可以转化为向量共线、内积为0等求解，就可以把所有几何问题都变成可计算的问题。这样的方法更加重视计算，并且除了传统的几何向量外，还可以构造直角坐标系从而获得坐标向量，运算更加方便。

基于极坐标与方程的解析几何：

这种方法其实可以回溯到当初学圆锥曲线的时期，把几何图形的相交、相切、相离抽象成方程解的问题。后来又学习过极坐标和参数方程，就会发现利用极坐标和参数方程去表示曲线实在是太方便了。这样的方法就可以把几何问题转化成一个代数问题来求解，大大提高了求解的效率。

在中学阶段总能够总结出一些常见的公理与定理，例如：

向量表示与坐标代换

向量并不陌生，但是可能接触最多的是认识到三维，并且还依赖于画图，中学阶段我们也仅仅是接触到了三维向量。其实不然，一个向量可以有不止三个轴，可以有5维，有10维，有10000维，你现在还能依靠图理解向量吗？事实上向量的维数可以是很多维，从代数的意义上你可以认为向量是一个集合，从几何的意义上你又可以认为向量是一个n维欧几里得空间中的一个点：

和二维、三维空间中的向量一样，高维空间中的向量同样可以进行加减运算、数量乘运算和数乘运算。但毕竟这是一门应用数学课程，我们不打算把太多精力放在任何一本线代课本里面都能找到的公式上，使用 Python 的NumPy 库举例子恐怕会更加直观。从程序设计的角度来看，如果读者接触过C语言应该会了解数组的概念，而在 C++ 语言中STL里面已经包含了 vector 类型。在 Python 中我们可以使用 NumPy 库来创建和操作向量，例如：

import numpy as np
#创建变量
x = np.array([1, 2, 3, 5, 8])
# array([1, 2, 3, 5, 8])

引入向量的目的并不仅仅是为了在几何图形中更好地表示方向和距离，而是为了利用代数的方法来解决几何问题。向量提供了一种将几何概念转化为代数表达式的方式，从而使得几何问题的解决变得更加简单和直接。

例如，在解决物理问题时，力、速度和加速度等物理量都可以用向量表示。通过向量的加减和数乘运算，我们可以直接计算出合力、相对速度等结果，而不需要借助复杂的几何图形。在计算机图形学中，向量被广泛用于表示和处理图形和动画。通过向量运算，我们可以实现图形的旋转、缩放、平移等变换，以及计算光线的反射和折射等效果。

解析几何法的本质就是利用函数与方程来表示不同的几何曲线。在中学阶段我们都学习过圆锥曲线的方程形式，但在实际问题中我们面临的曲线会更加复杂。尤其是在三维空间中的曲线与曲面，可能会用到多元函数去进行表示，也可能用极坐标或参数方程更加方便，但不管怎么说，解析几何方法的本质就是把各种几何问题都转化为代数问题求解。解方程比起复杂的分析，更依靠计算，而这恰恰是程序所擅长的。

在数学中，坐标变换通常涉及到一系列的矩阵运算，这些矩阵描述了一个坐标系相对于另一个坐标系的位置和方向。旋转变换就是其中的一个典型例子。当我们说一个坐标系相对于另一个坐标系进行了旋转，我们通常是指它绕着一个轴或者点旋转了一定的角度。二维空间的旋转可以简化为点绕原点旋转，而三维空间则涉及到更复杂的轴向旋转。

在二维空间中，如果我们要将坐标系绕原点旋转一个角度，就可以通过旋转矩阵来实现。旋转矩阵是一个非常简单而又强大的工具，它可以将原始坐标系中的点通过线性变换映射到新坐标系中。对于逆时针旋转，二维旋转矩阵的形式是

这里，$\theta$是旋转角度，当应用这个旋转矩阵于一个点$(x,y)$，它会给出新的坐标$(x\prime ,y\prime )$
这表示了原始点在新坐标系中的位置。

使用NumPy进行这样的变换非常简单。首先，我们创建一个表示点坐标的NumPy数组，然后创建表示旋转矩阵的二维数组。

通过对这两个数组进行点积运算（也就是矩阵乘法），我们就可以得到新的坐标，在Python中可以这样实现：

#二维直角坐标系
#设定旋转角度，以30度为例
#将30度转化为弧度
theta=np.radians(30)
#创建旋转矩阵
Rotation_matrix=np.array([
    [np.cos(theta),-np.sin(theta)],
    [np.sin(theta),np.cos(theta)]
    ])

#假设我们有一个点
a=5
b=3
point=np.array([a,b])
#t通过旋转得到这个点的坐标
rotated_point=Rotation_matrix.dot(point)

print("原坐标为：",point)
print("旋转后的坐标为：",rotated_point)
# 原坐标为: [5 3]
# 旋转后的坐标为: [2.83012702 5.09807621]

此示例代码中，旋转角度是预设的，你可以根据实际情况调整。通过这种方式，我们能够将几何问题通过坐标变换转化为代数问题，使用编程方法来进行高效的计算。这不仅仅适用于理论数学问题，同样也适用于工程、物理学、计算机图形学以及机器人技术等多个领域中。

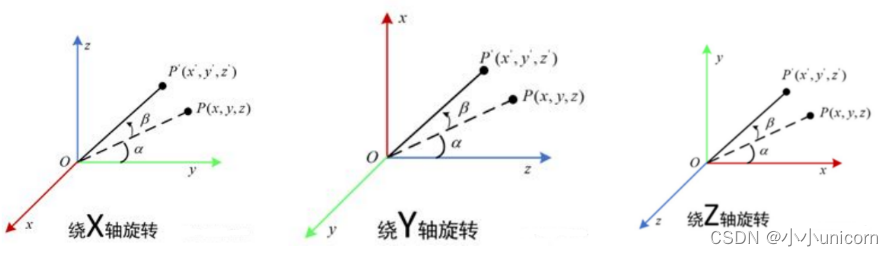
在三维空间中，物体的旋转可以围绕三个主轴进行：$\mathrm{x}$轴， $\mathrm{y}$轴和$\mathrm{z}$轴。这些轴旋转代表了不同方向的运动，并且可以通过旋转矩阵来数学描述。例如，一个点$P(x,y,z)$绕$\mathrm{z}$轴旋转角度$\alpha$可以表示为

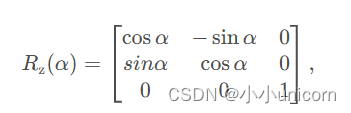
这个旋转保持$z$坐标不变，同时在$XY$平面上变换$x$和$y$坐标。相似地，点P绕$y$轴旋转角度β的旋转矩阵为:

这个旋转保持$y$坐标不变，同时在$XZ$平面上变换$x$和$z$坐标。而点$P$绕$x$轴旋转角度γ的旋转矩阵为


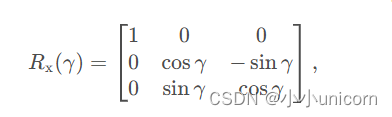
在实际应用中，如机器人学、航空航天和计算机图形学，旋转顺序对于模拟和预测物体如何移动至关重要。例如，飞机的姿态控制就极依赖于绕不同轴的旋转顺序，以精确地模拟和控制飞机的行动。在三维建模和动画制作中，这些旋转变换同样是创建动态、逼真场景的基础。

在Python中，利用NumPy库，我们可以使用如下代码片段来实现三维旋转变换：

#三维直角坐标系
#定义旋转角度，以弧度为单位
alpha=np.radians(30)#绕Z轴转动
beta=np.radians(45)#绕Y轴转动
gamma=np.radians(60)#绕X轴转动

#定义旋转矩阵
R_z=np.array([[np.cos(alpha),