本专栏内容为:算法学习专栏,分为优选算法专栏,贪心算法专栏,动态规划专栏以及递归,搜索与回溯算法专栏四部分。 通过本专栏的深入学习,你可以了解并掌握算法。
💓博主csdn个人主页:小小unicorn
⏩专栏分类:acwing语法基础
🚚代码仓库:小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识
专题一
1.A+B
来源:A+B
题目描述:

这个题比较简单,注意变量开longlong即可
代码解决:
#include<iostream>
using namespace std;
int main()
{
long long a,b;
cin>>a>>b;
cout<<a+b;
return 0;
}
运行结果:

2.差
题目来源:差
题目描述:

这个题比较简单,直接打印结果即可。
代码解决:
#include<iostream>
using namespace std;
int main()
{
long long a,b,c,d;
cin>>a>>b>>c>>d;
cout<<"DIFERENCA = "<<(a*b-c*d);
return 0;
}
3.圆的面积
来源:圆的面积
题目描述:

这个题目我们要注意一下最后输出的结果保留的是四位数,我们使用printf函数来控制打印输出。
#include<iostream>
using namespace std;
#define PI 3.14159
int main()
{
double R,A;
cin>>R;
A=PI*R*R;
printf("A=%.4lf", A);
return 0;
}
运行结果:

4.平均数1
来源:平均数1
题目描述:

这道题主要要理解加权二字:
这里的权重就是指的加权平均里的权,平均不仅仅只有五五开 的,也有任意开的,这就是3.5,7.5开的
最后除的不是2而是3.5+7.5的结果
代码解决:
#include<iostream>
using namespace std;
int main()
{
double a,b,x;
cin>>a>>b;
x=(a*3.5+b*7.5 )/11;//11=3.5+7.5
printf("MEDIA = %.5lf",x);
return 0;
}
结果:

5.工资
来源:工资
题目描述:

本题还是标准的输出输入,按照要求进行撰写代码即可。
代码解决:
#include<iostream>
using namespace std;
int main()
{
long long number,time;//员工编号,工作时间
double Hourlywages;//时薪
cin>>number>>time>>Hourlywages;
double money=Hourlywages*time;
cout<<"NUMBER = "<<number<<endl;
printf("SALARY = U$ %.2lf",money);
return 0;
}
结果显示:

6.油耗
来源:油耗
题目描述:

代码解决:
#include<iostream>
using namespace std;
int main()
{
int journey;//路程
double Fuelconsumption;//耗油量
cin>>journey>>Fuelconsumption;
printf("%.3lf km/l",journey / Fuelconsumption);
return 0;
}
结果显示:

7.两点间的距离
来源:两点间的距离
题目描述:

这里我们可以直接输出结果,直接计算。
这里我们用到了两个数学里面的库函数sqrt和pow函数:
pow函数用于计算一个数的幂。其基本语法如下:
double pow(double base, double exponent);
参数:
base:底数(类型为double)。exponent:指数(类型为double)。
返回值:
- 返回
base的exponent次幂(base^exponent)。
示例:
#include <iostream>
#include <cmath>
int main()
{
double result = pow(2.0, 3.0); // 2的3次方
std::cout << "2^3 = " << result << std::endl; // 输出: 2^3 = 8
return 0;
}
sqrt函数
sqrt函数用于计算一个数的平方根。其基本语法如下:
double sqrt(double x);
- 参数:
x:非负数(类型为double),其平方根将被计算。
- 返回值:
- 返回
x的平方根,如果x为负数,则返回NaN(不是一个数字)。
- 返回
示例:
include <iostream>
#include <cmath>
int main()
{
double result = sqrt(16.0); // 16的平方根
std::cout << "sqrt(16) = " << result << std::endl; // 输出: sqrt(16) = 4
return 0;
}
注意事项
- 使用这两个函数时,确保包含头文件
<cmath>。 - 计算结果可能会受到精度的影响,特别是在使用浮点数时。
- 当
pow函数的指数为负数时,结果为1除以底数的正幂。 - 对于负数,
sqrt会返回NaN,在实际应用中需要做适当的错误处理。
代码解决:
#include<iostream>
#include<cmath>
using namespace std;
int main()
{
double x1,y1;
double x2,y2;
cin>>x1>>y1>>x2>>y2;
printf("%.4lf",sqrt(pow(x2 - x1, 2) + pow(y2 - y1, 2)));
//printf("%.4lf\n ", sqrt ( ( x1 - x2) * ( x1 - x2 ) + ( y1 - y2 ) * ( y1 - y2 ) ) );
}
8.钞票(1)
来源:钞票
题目描述:


代码解决:
#include<iostream>
using namespace std;
int main()
{
int money, a[7] = {100, 50, 20, 10, 5, 2, 1};
cin >> money;
cout<<money<<endl;
for (int i = 0; i < 7; i ++ )
{
printf("%d nota(s) de R$ %d,00\n", money / a[i], a[i]);
money %= a[i];
}
return 0;
}
9.时间转换(2)
来源:时间转换
题目描述:
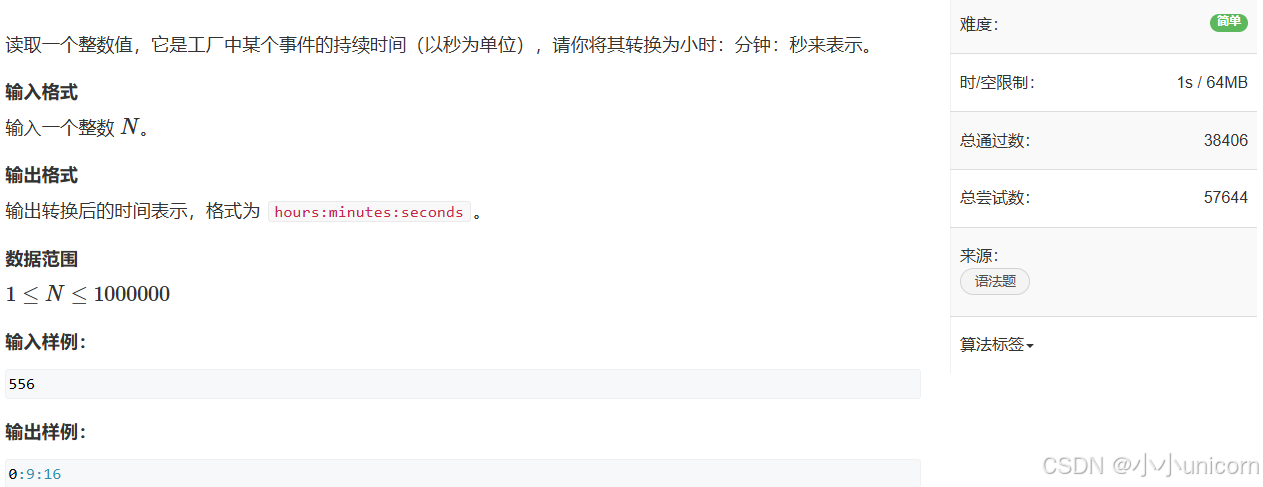
代码解决:
#include <iostream>
using namespace std;
int main()
{
int t;
cin >> t;
int h = t / 3600;
int m = t % 3600 / 60;
int s = t % 60;
cout << h << ':' << m << ':' << s << endl;
return 0;
}
详细说明
- 输入:用户输入一个整数
t,表示总秒数。 - 计算小时:使用整数除法
/将总秒数t转换为小时,t / 3600。 - 计算分钟:使用取模运算
%先求出剩余的秒数(t % 3600),再将其转换为分钟,(t % 3600) / 60。 - 计算秒:直接对
t取模,t % 60得到剩余的秒数。 - 输出:使用
cout输出格式为h:m:s。
示例:
假设输入3661,程序将输出1:1:1,表示1小时1分钟1秒。
改进
你可以考虑添加输入验证,以确保输入的秒数是非负的,或者在输出时格式化为两位数(例如,01:01:01),使输出更加美观。下面是一个改进的版本:
#include <iostream>
#include <iomanip> // 用于 std::setw 和 std::setfill
using namespace std;
int main()
{
int t;
cin >> t;
// 输入验证
if (t < 0)
{
cout << "请输入一个非负整数!" << endl;
return 1;
}
int h = t / 3600;
int m = (t % 3600) / 60;
int s = t % 60;
// 使用setw和setfill格式化输出
cout << setw(2) << setfill('0') << h << ':'
<< setw(2) << setfill('0') << m << ':'
<< setw(2) << setfill('0') << s << endl;
return 0;
}
这样可以保证输出的小时、分钟和秒都是两位数,格式更加整齐。
结果显示:

10.简单乘积(带你用11种解法进行解决)
来源:简单乘积
题目描述:

代码解决:
直接做:
#include<iostream>
using namespace std;
int main()
{
int a, b;
cin >> a >> b;
cout << "PROD = " << a * b << endl;
return 0;
}
用二分处理,先把负数转换,然后二分
#include<iostream>
using namespace std;
int f = 0;//数的状态(0,-..,...)
int main()
{
int a, b;
cin >> a >> b;
if(a == 0 || b == 0) f = 2;//处理状态
else if(a < 0 && b >= 0 || b < 0 && a >= 0)
{
f = 1;
if(a < 0) a = a * -1;
else b = b * -1;
}
int l = -100000000, r = 100000000;
while(r - l >= 1)
{
int mid = (l + r) / 2;//二分
if(mid >= a * b) r = mid;
else l = mid + 1;
}
if(f == 2)
{
cout <<"PROD = " << l;
}
else if(f == 0)
{
cout <<"PROD = " << l;
}
else cout << "PROD = -" << l;
}
高精度算法
#include <iostream>
#include <vector>
using namespace std;
vector<int> f(vector<int> &a, int b)//处理函数
{
vector<int> c;//定义结果
int x = 0;
for (int i = 0; i < a.size() || x; i ++ )//一位一位运算
{
if (i < a.size()) x += a[i] * b;//每次把a【i】乘b
c.push_back(x % 10);
x = x / 10;
}
while (c.size() > 1 && c.back() == 0) c.pop_back();
return c;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> a2;
for (int i = a.size() - 1; i >= 0; i -- ) a2.push_back(a[i] - '0');
auto c = f(a2, b);
for (int i = c.size() - 1; i >= 0; i -- ) printf("%d", c[i]);
return 0;
}
位运算
#include <stdio.h>
int add(int a, int b)
{
while (b)
{
int x = a ^ b;
int y = (a & b) << 1;
a = x;
b = y;
}
return a;
}
int main()
{
int a, b;
int res = 0;
cin>>a>>b;
if (b < 0)
{
a = add(~a, 1);
b = add(~b, 1);
}
while (b)
{
if (b & 1) res = add(res, a);
a <<= 1;
b >>= 1;
}
printf("PROD = %d", res);
return 0;
}
SPFA解法:
SPFA(Shortest Path Faster Algorithm)是一种用于求解带权图中单源最短路径的算法,尤其适合于稀疏图。它是Bellman-Ford算法的优化版本,利用队列来实现更高效的松弛操作。以下是SPFA算法的基本思想、步骤和C++实现。
算法基本思想
- 初始化:将源点到自身的距离设置为0,其他点的距离设置为无穷大(或一个较大的数)。
- 使用队列:将源点加入队列。
- 松弛操作:从队列中取出一个顶点,检查它的邻接边。如果通过该顶点到达邻接点的距离比当前已知距离小,则更新距离,并将该邻接点加入队列(如果它还不在队列中)。
- 重复:继续处理队列中的顶点,直到队列为空。
#include <stdio.h>
#include <string.h>
const int N = 10010;
int e[N], ne[N], w[N], h[N], idx;
int dist[N];
bool state[N];
int q[N];
int hh, tt;
void add(int a, int b, int c)
{
e[ ++ idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
}
int spfa(int end)
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
state[1] = true;
q[0] = 1;
while (hh <= tt)
{
int t = q[hh ++ ];
state[t] = false;
for (int i = h[t]; i; i = ne[i])
if (dist[e[i]] > dist[t] + w[i])
{
dist[e[i]] = dist[t] + w[i];
if (!state[e[i]])
{
state[e[i]] = true;
q[ ++ tt] = e[i];
}
}
}
return dist[end];
}
int main()
{
int a, n;
scanf("%d %d", &a, &n);
if(n < 0) a = -a, n = -n;
n ++ ;
for (int i = 1; i < n; i ++ )
add(i, i + 1, a);
printf("PROD = %d", spfa(n));
return 0;
}
本代码实现了一个使用SPFA算法来计算从节点1到节点n的最短路径的程序。这个程序特别之处在于它通过边的权重进行动态的图构建。以下是代码的详细解释和一些建议。
代码解释
- 数据结构
e[N]:邻接表中的边的目标节点。ne[N]:邻接表中的下一个边的索引。w[N]:边的权重。h[N]:每个节点的邻接链表的头部。dist[N]:存储从源节点到各个节点的最短距离。state[N]:标记节点是否在队列中。q[N]:用于实现队列的数组,存储当前待处理的节点。
add函数
这个函数用于向图中添加一条边。它将边的目标节点、权重和链表结构进行适当的更新。
void add(int a, int b, int c)
{
e[++idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
}
spfa函数
该函数实现了SPFA算法,计算从节点1到指定目标节点的最短距离。
int spfa(int end)
{
memset(dist, 0x3f, sizeof dist); // 初始化距离为无穷大
dist[1] = 0; // 源节点到自身的距离为0
state[1] = true; // 标记源节点在队列中
q[0] = 1; // 将源节点入队
hh = 0; // 队头
tt = 0; // 队尾
while (hh <= tt)
{
int t = q[hh++]; // 取出队头元素
state[t] = false; // 标记为不在队列中
for (int i = h[t]; i; i = ne[i]) // 遍历邻接边
if (dist[e[i]] > dist[t] + w[i]) // 松弛操作
{
dist[e[i]] = dist[t] + w[i];
if (!state[e[i]]) // 如果不在队列中
{
state[e[i]] = true; // 标记为在队列中
q[++tt] = e[i]; // 入队
}
}
}
return dist[end]; // 返回到目标节点的距离
}
main函数
主函数负责输入和初始化图。
int main()
{
int a, n;
scanf("%d %d", &a, &n);
if (n < 0) a = -a, n = -n; // 处理负数的情况
n++;
for (int i = 1; i < n; i++)
add(i, i + 1, a); // 添加边
printf("PROD = %d", spfa(n)); // 输出结果
return 0;
}
代码逻辑
- 输入的
a表示每条边的权重,n表示节点数。 - 如果
n为负数,则将其转换为正数,并反向a的符号。 - 构建了一个从1到
n的线性图,每条边的权重为a。 - 使用SPFA算法计算从节点1到节点
n的最短路径,并输出结果。
堆优化dijkstra解法(手写堆)
#include <stdio.h>
#include <string.h>
const int N = 10010;
int e[N], h[N], ne[N], w[N], idx;
int dist[N];
bool state[N];
int heap_first[N], heap_second[N];
int size;
void add(int a, int b, int c)
{
e[ ++ idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
}
void heap_swap(int i, int j)
{
if (i ^ j)
{
heap_first[i] ^= heap_first[j];
heap_first[j] ^= heap_first[i];
heap_first[i] ^= heap_first[j];
heap_second[i] ^= heap_second[j];
heap_second[j] ^= heap_second[i];
heap_second[i] ^= heap_second[j];
}
}
void down(int p)
{
int t = p;
if (p << 1 <= size && heap_first[p << 1] < heap_first[t])
t = p << 1;
if ((p << 1 | 1) <= size && heap_first[p << 1 | 1] < heap_first[t])
t = p << 1 | 1;
if (t ^ p)
{
heap_swap(t, p);
down(t);
}
}
void up(int p)
{
while (p >> 1 && heap_first[p >> 1] > heap_first[p])
{
heap_swap(p >> 1, p);
p >>= 1;
}
}
void insert(int first, int second)
{
size ++ ;
heap_first[size] = first;
heap_second[size] = second;
up(size);
}
void erase(int p)
{
heap_swap(p, size -- );
up(p);
down(p);
}
int dijkstra(int end)
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
insert(0, 1);
while (size)
{
int t = heap_second[1];
erase(1);
if (state[t])continue;
state[t] = true;
for (int i = h[t]; i; i = ne[i])
if (dist[e[i]] > dist[t] + w[i])
{
dist[e[i]] = dist[t] + w[i];
insert(dist[e[i]], e[i]);
}
}
return dist[end];
}
int main()
{
int a, n, f = 1;
scanf("%d %d", &a, &n);
if (n < 0) n = -n, a = -a;
if (a < 0) f = -f, a = -a;
n ++ ;
for (int i = 1; i < n; i ++ )
add(i, i + 1, a);
printf("PROD = %d\n", f * dijkstra(n));
return 0;
}
代码解释
- 数据结构
e[N]:邻接表中的边的目标节点。h[N]:每个节点的邻接链表的头部。ne[N]:邻接表中的下一个边的索引。w[N]:边的权重。dist[N]:存储从源节点到各个节点的最短距离。state[N]:标记节点是否已经被处理。heap_first[N]:堆中存储的距离。heap_second[N]:堆中存储的节点索引。size:当前堆的大小。
add函数
这个函数向图中添加一条边。它将边的目标节点、权重和链表结构进行适当的更新。
void add(int a, int b, int c)
{
e[++idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
}
- 堆相关操作
heap_swap:交换堆中两个节点的值。
void heap_swap(int i, int j)
{
if (i ^ j)
{
heap_first[i] ^= heap_first[j];
heap_first[j] ^= heap_first[i];
heap_first[i] ^= heap_first[j];
heap_second[i] ^= heap_second[j];
heap_second[j] ^= heap_second[i];
heap_second[i] ^= heap_second[j];
}
}
down:调整堆,从节点p向下调整。
void down(int p)
{
int t = p;
if (p << 1 <= size && heap_first[p << 1] < heap_first[t])
t = p << 1;
if ((p << 1 | 1) <= size && heap_first[p << 1 | 1] < heap_first[t])
t = p << 1 | 1;
if (t ^ p)
{
heap_swap(t, p);
down(t);
}
}
up:调整堆,从节点p向上调整。
void up(int p)
{
while (p >> 1 && heap_first[p >> 1] > heap_first[p])
{
heap_swap(p >> 1, p);
p >>= 1;
}
}
insert:将一个新的节点插入到堆中。
void insert(int first, int second)
{
size++;
heap_first[size] = first;
heap_second[size] = second;
up(size);
}
erase:删除堆顶元素并调整堆。
void erase(int p)
{
heap_swap(p, size--);
up(p);
down(p);
}
- Dijkstra 算法实现
dijkstra函数计算从节点1到目标节点的最短距离。
int dijkstra(int end)
{
memset(dist, 0x3f, sizeof dist); // 初始化距离为无穷大
dist[1] = 0; // 源节点到自身的距离为0
insert(0, 1); // 插入源节点
while (size)
{
int t = heap_second[1]; // 取出堆顶节点
erase(1); // 删除堆顶
if (state[t]) continue; // 如果已处理,跳过
state[t] = true; // 标记为已处理
for (int i = h[t]; i; i = ne[i]) // 遍历邻接边
if (dist[e[i]] > dist[t] + w[i]) // 松弛操作
{
dist[e[i]] = dist[t] + w[i];
insert(dist[e[i]], e[i]); // 插入新的距离
}
}
return dist[end]; // 返回到目标节点的距离
}
main函数
主函数负责输入和初始化图。
int main()
{
int a, n, f = 1;
scanf("%d %d", &a, &n);
if (n < 0) n = -n, a = -a; // 处理负数情况
if (a < 0) f = -f, a = -a; // 处理权重负数情况
n++;
for (int i = 1; i < n; i++)
add(i, i + 1, a); // 添加边
printf("PROD = %d\n", f * dijkstra(n)); // 输出结果
return 0;
}
代码逻辑
- 输入的
a表示每条边的权重,n表示节点数。 - 如果
n或a为负数,进行相应的转换。 - 构建了一个从1到
n的线性图,每条边的权重为a。 - 使用堆优化的Dijkstra算法计算从节点1到节点
n的最短路径,并输出结果。
bfs版
#include <stdio.h>
const int N = 10010;
int e[N], ne[N], h[N], w[N], idx;
int q[N], hh, tt;
int dist[N];
bool state[N];
void add(int a, int b, int c)
{
e[ ++ idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
}
int bfs(int end)
{
q[0] = 1;
state[1] = true;
while (hh <= tt)
{
int t = q[hh ++ ];
if (t == end) return dist[t];
for (int i = h[t]; i; i = ne[i])
if (!state[e[i]])
{
state[e[i]] = true;
q[ ++ tt] = e[i];
dist[e[i]] = dist[t] + w[i];
}
}
return -1;
}
int main()
{
int a, n;
scanf("%d %d", &a, &n);
printf("PROD = ");
if (n < 0) n = -n, a = -a;
if (a < 0) putchar('-'), a = -a;
n ++ ;
for (int i = 1; i < n; i ++ )
add(i, i + 1, a);
printf("%d", bfs(n));
return 0;
}
DFS版本
#include <stdio.h>
const int N = 10010;
int e[N], h[N], ne[N], w[N], idx;
int dist[N];
bool state[N];
void add(int a, int b, int c)
{
e[ ++ idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
}
void dfs(int t)
{
for (int i = h[t]; i; i = ne[i])
if (!state[e[i]])
{
state[t] = true;
dfs(e[i]);
dist[t] = dist[e[i]] + w[i];
state[t] = false;
}
}
int main()
{
int a, n;
scanf("%d %d", &a, &n);
printf("PROD = ");
if (n < 0) n = -n, a = -a;
if (a < 0) putchar('-'), a = -a;
n ++ ;
for (int i = 1; i < n; i ++ )
add(i, i + 1, a);
dfs(1);
printf("%d", dist[1]);
return 0;
}
kruskal解法
Kruskal算法是一种用于寻找最小生成树的贪心算法。它通过将图的边按权重排序,逐步选择权重最小的边,前提是选择后不会形成环,直到树中包含所有顶点。
#include <stdio.h>
#include <string.h>
const int N = 10010;
struct Edge
{
int a, b, w;
}edges[N];
int a, n;
int res;
int fa[N];
int find(int x)
{
if (x ^ fa[x]) fa[x] = find(fa[x]);
return fa[x];
}
int kruskal()
{
for (int i = 1; i <= n; i ++ )
{
int a = find(edges[i].a);
int b = find(edges[i].b);
int w = edges[i].w;
if (a ^ b)
{
fa[a] = b;
res += w;
}
}
return res;
}
int main()
{
scanf("%d %d", &a, &n);
printf("PROD = ");
if (n < 0) n = -n, a = -a;
if (a < 0) putchar('-'), a = -a;
n ++ ;
for (int i = 1; i < n; i ++ )
{
edges[i].a = i;
edges[i].b = i + 1;
edges[i].w = a;
fa[i] = i;
}
printf("%d", kruskal());
return 0;
}
树状数组解法
#include <stdio.h>
#include <string.h>
const int N = 10010;
int a, n;
int tr[N];
int lowbit(int x)
{
return x & -x;
}
void add(int x, int c)
{
for (int i = x; i <= n; i += lowbit(i))
tr[i] += c;
}
int sum(int x)
{
int res = 0;
for (int i = x; i; i -= lowbit(i))
res += tr[i];
return res;
}
int main()
{
scanf("%d %d", &a, &n);
printf("PROD = ");
if (n < 0) n = -n, a = -a;
for (int i = 1; i <= n; i ++ )
add(i, a);
printf("%d", sum(n));
return 0;
}
并查集解法
#include <stdio.h>
#include <string.h>
const int N = 10010;
int a, n;
int fa[N], size[N];
int find(int x)
{
if (fa[x] ^ x) fa[x] = find(fa[x]);
return fa[x];
}
void merge(int a, int b)
{
a = find(a), b = find(b);
size[b] += size[a];
fa[a] = b;
}
int main()
{
scanf("%d %d", &a, &n);
printf("PROD = ");
if (n < 0) n = -n, a = -a;
for (int i = 1; i <= n; i ++ )
fa[i] = i, size[i] = a;
for (int i = 1; i < n; i ++ )
merge(i, n);
printf("%d", size[n]);
return 0;
}
11.简单计算
来源:简单计算
题目描述:

代码解决:
#include<iostream>
using namespace std;
int main()
{
int code,n;
double price,sum=0.0;
for(int i=1;i<=2;i++)
cin>>code>>n>>price,sum+=n*price;
printf("VALOR A PAGAR: R$ %.2lf",sum);
return 0;
}
结果显示:

12.球的体积
来源:球的体积
题目描述:

代码解决:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int r; scanf("%d", &r);
printf("VOLUME = %.3f", 4 / 3.0 * 3.14159 * r * r * r);
return 0;
}
结果显示:
13.面积
来源:面积
题目描述:


代码解决:
#include<bits/stdc++.h>
using namespace std;
int main()
{
double a, b, c;
cin>>a>>b>>c;
printf("TRIANGULO: %.3f\n", a * c / 2);
printf("CIRCULO: %.3f\n", 3.14159 * c * c);
printf("TRAPEZIO: %.3f\n", (a + b) * c / 2);
printf("QUADRADO: %.3f\n", b * b);
printf("RETANGULO: %.3f\n", a * b);
return 0;
}
结果显示:

14.平均数2
来源:平均数2
题目描述:


代码解决:
#include <iostream>
using namespace std;
int main()
{
double a, b, c;
cin >> a >> b >> c;
printf("MEDIA = %.1lf", (a * 2 + b * 3 + c * 5) / 10.0);
return 0;
}
结果显示:

15.工资和奖金
来源:工资和奖金
题目描述:


代码解决:
#include <cstdio>
#include<iostream>
using namespace std;
int main()
{
char a[10];
double b, c;
cin>>a>>b>>c;
printf("TOTAL = R$ %.2lf", b + c * 0.15);
return 0;
}
结果显示:

16.最大值
来源:最大值
题目描述:

代码解决:
算法1:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int a,b,c,max;
cin>>a>>b>>c;
if(a>b)
if(a>c)
max=a;
else
max=c;
else
if(b>c)
max=b;
else
max=c;
cout<<max<<" eh o maior";
return 0;
}
算法2:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int a,b,c,max;
cin>>a>>b>>c;
max=(a+b+abs(a-b))/2;
max=(max+c+abs(max-c))/2;
return 0;
}

算法3:
#include <iostream>
#include <algorithm>///一定要写这个头文件
using namespace std;
int main(){
int a,b,c;
int max1 = 0;
cin>>a>>b>>c;
max1 = max(a,b);///调用库函数max
max1 = max(max1,c);
cout<<max1<<" eh o maior"<<endl;
return 0;
}
结果显示:

有人可能有疑惑:
#include<bits/stdc++.h>
是个什么东西,这里解答一下,这个被叫做万能头文件(但不是所有编译器都原生支持,比如VS系列)
这个库内起码包含了如下:
#include <iostream>//io流
#include <cstdio>//io流
#include <fstream>//文件的输入和输出
#include <algorithm>//算法
#include <cmath>//数学
#include <deque>//双端队列
#include <vector>//数据
#include <queue>//队列
#include <string>//字符串
#include <cstring>//字符串
#include <map>//关联容器,用于存储键值对,并根据键进行排序。它通常用于快速查找和关联数据
#include <stack>//栈
#include <set>//关联容器,用于存储唯一的元素,并根据元素的顺序自动排序
17.距离
来源:距离
题目描述:

代码解决:
#include <bits/stdc++.h>
using namespace std;
int n;
int main() {
scanf("%d", &n);
printf("%d minutos", n << 1);
return 0;
}
结果显示:

18.燃料消耗
来源:燃料消耗
题目描述:

代码解决:
//本题只用scanf和printf可以做出来,但有两个小坑
#include<bits/stdc++.h>
using namespace std;
long long s,t;
//第一个坑,要开long long,因为数据有点大,int可能会爆0
double ans;
int main()
{
scanf("%lld%lld",&t,&s);
ans=t*s*1.0/12;
//这道题第二个坑,乘1.0来保存小数点后的数
printf("%.3lf",ans);
return 0;
}
结果显示:

19.钞票和硬币
来源:钞票和硬币
题目描述:


代码解决:
#include <iostream>
using namespace std;
int main()
{
double n;
cin>>n;
int m=(int)(n*100);
int a[12]={10000,5000,2000,1000,500,200,100,50,25,10,5,1};
printf("NOTAS:\n");
for(int i=0;i<12;i++)
{
if(i<6){printf("%d nota(s) de R$ %.2f\n",m/a[i],(float)a[i]/100);m%=a[i];}
if(i==6)printf("MOEDAS:\n");
if(i>=6){printf("%d moeda(s) de R$ %.2f\n",m/a[i],(float)a[i]/100);m%=a[i];}
}
}
结果显示:
20.天数转换
来源:天数转换
题目描述:

代码解决:
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
printf("%d ano(s)\n", n / 365);
n -= n / 365 * 365;
printf("%d mes(es)\n", n / 30);
n -= n / 30 * 30;
printf("%d dia(s)\n", n);
return 0;
}
结果显示:





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










