4 dp打题-CSDN博客

本文链接：https://blog.csdn.net/weixin_72770922/article/details/136527462

文章展示了五个C++代码片段，涉及数组操作、动态规划和递归方法，用于求解最大值问题。第一个是计算二维数组的累加和，第二个是使用动态规划解决任务分配问题，第三个是路径上的最大分数问题，第四个是数组更新操作，第五个是结合数组和动态规划求解特定游戏策略收益。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

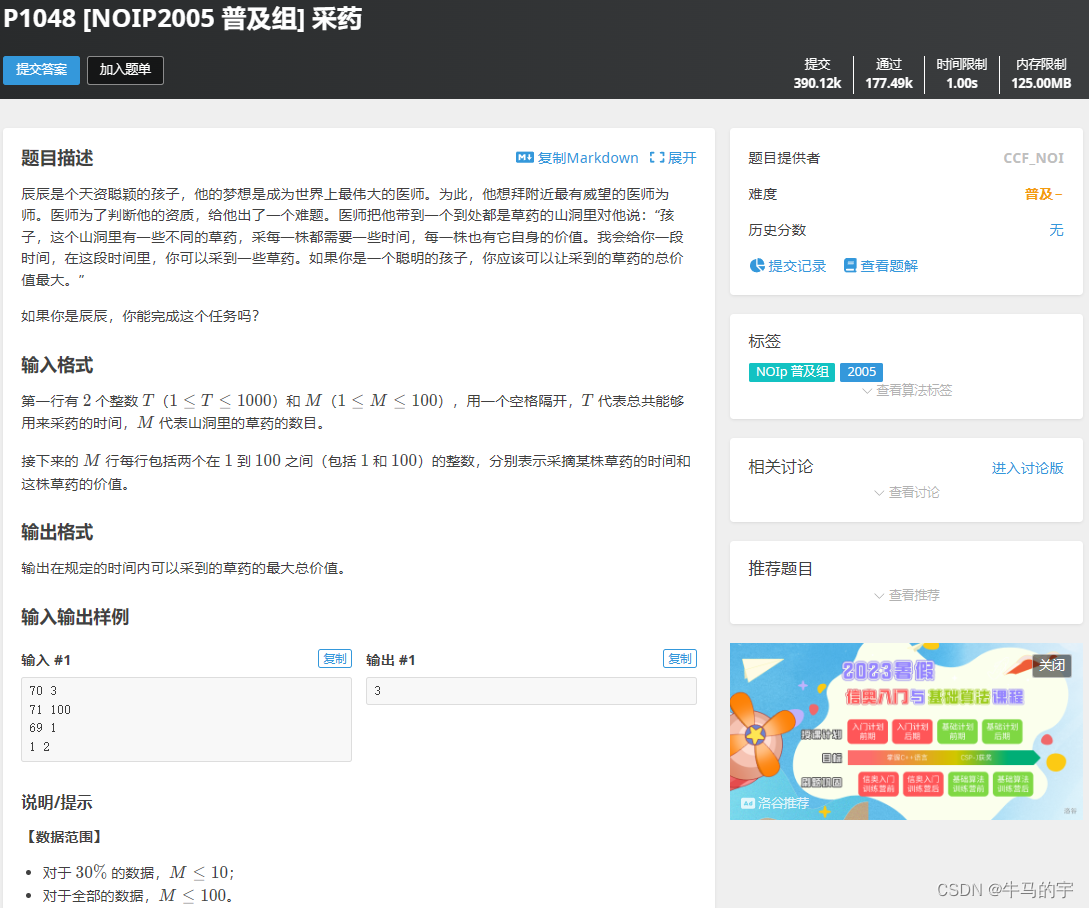
#include<iostream>
using namespace std;
#include<algorithm>
int const N = 1e3 + 10;
int arr[N][N];
int n;
int main()
{
	cin >> n;
	for (int i = 1;i <= n;i++)
	{
		for (int j = 1;j <= i;j++)
		{
			cin >> arr[i][j];
		}
	}
	for (int i = 1;i <= n;i++)
	{
		for (int j = 1;j <= i;j++)
		{
			arr[i][j] += max(arr[i - 1][j - 1], arr[i - 1][j]);
		}
	}
	int ans = 0;
	for (int i = 1;i <= n;i++)
	{
		ans = max(ans, arr[n][i]);
	}
	cout << ans << endl;
	return 0;
}

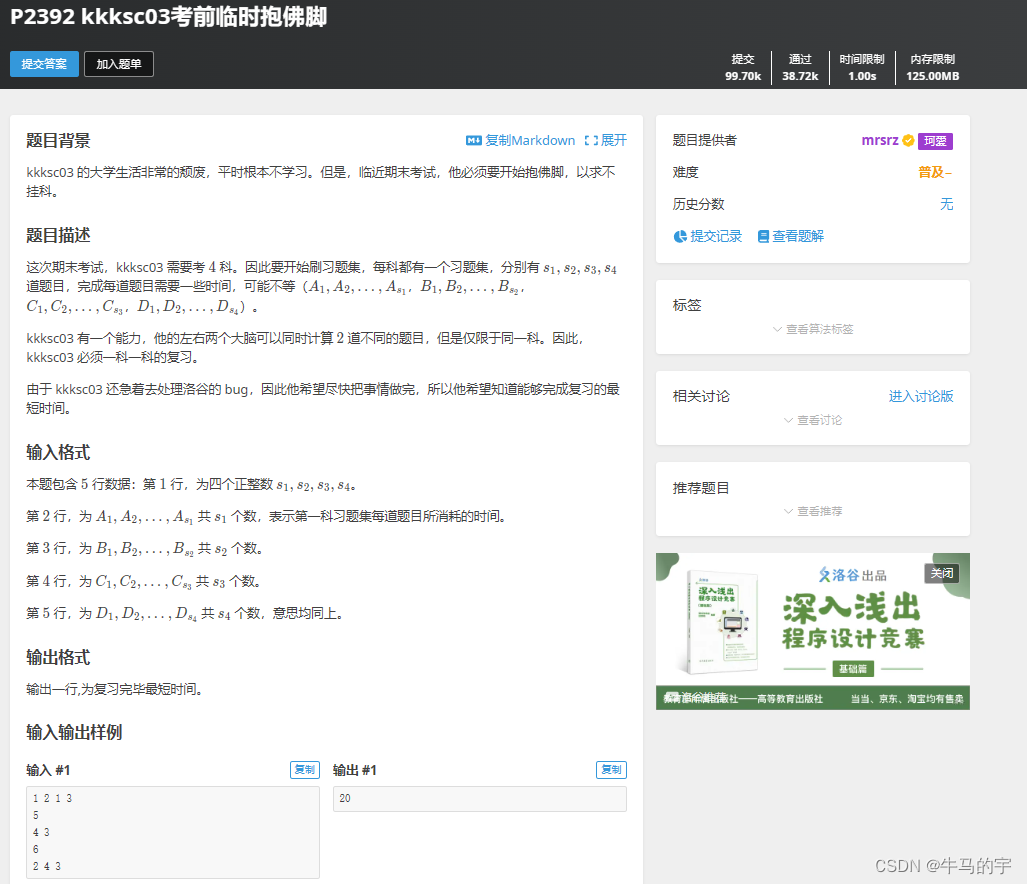
#include<iostream>
#include<algorithm>
using namespace std;
int t, n;
int const N = 110;
int arrt[N];
int arrs[N];
int dp[1010][110];
int main()
{
	cin >> t >> n;
	for (int i = 1;i <= n;i++)
	{
		cin >> arrt[i] >> arrs[i];
	}
	for (int i = 0;i <= t;i++)
	{
		for (int j = 1;j <= n;j++)
		{
			if (i >= arrt[j])
			{
				dp[i][j] = max(dp[i][j - 1], dp[i - arrt[j]][j - 1] + arrs[j]);
			}
			else
			{
				dp[i][j] = dp[i][j - 1];
			}
		}
	}
	cout << dp[t][n] << endl;
	return 0;
}

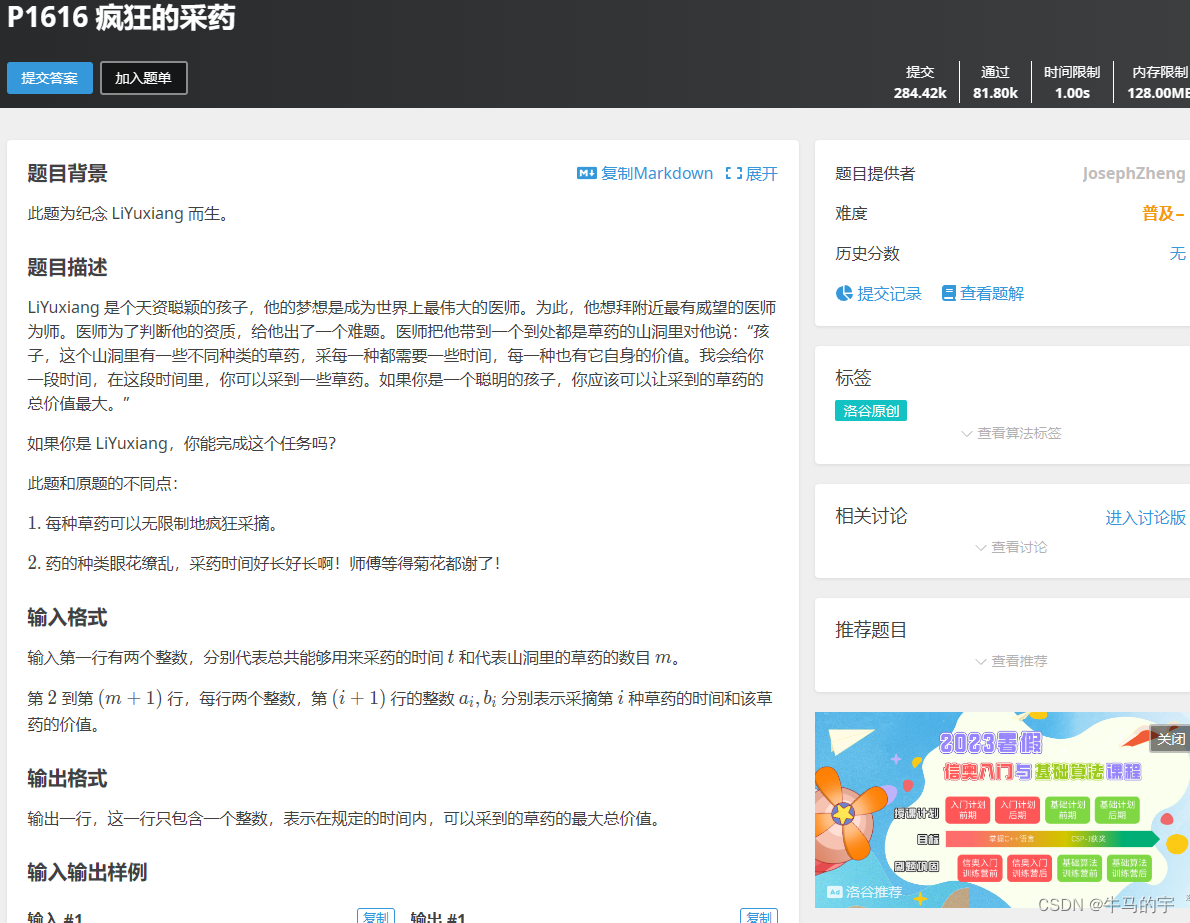
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int s[5];
int arr[5][100];
int ans;
int ans1, ans2;
void dfs(int x, int y)
{
	//cout << " flag:  "<<ans1 << " " << ans2 << endl;
	if (y > s[x])
	{
		int test = max(ans1, ans2);
		ans = min(test, ans);
		return;
	}
	ans1 += arr[x][y];
	dfs(x, y + 1);
	ans1 -= arr[x][y];
	ans2 += arr[x][y];
	dfs(x, y + 1);
	ans2 -= arr[x][y];
	
}
int main()
{
	int res = 0;
	for (int i = 1;i <= 4;i++)
	{
		cin >> s[i];
	}
	for (int i = 1;i <= 4;i++)
	{
		for (int j = 1;j <= s[i];j++)
		{
			cin >> arr[i][j];
		}
		ans = 10000000;
		ans1 = ans2 = 0;
		dfs(i, 1);
		res += ans;
	}
	
	cout << res << endl;
	return 0;
}

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<algorithm>
using namespace std;
int t, n;
long long arrt[10000010];
long long arrs[10010];
long long f[10010];
int main()
{
	cin >> t >> n;
	for (int i = 1;i <= n;i++)
	{
		scanf("%d%d", &arrt[i],&arrs[i]);
	}
	for (int i = 1;i <= n;i++)
	{
		for (int j = arrt[i];j <= t;j++)
		{
			f[j] = max(f[j], f[j - arrt[i]] + arrs[i]);
		}
	}
	cout << f[t] << endl;
	return 0;
}

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<algorithm>
using namespace std;
int m, n;
int f[20010];
int w[40];
int main()
{
	cin >> m >> n;
	for (int i = 1;i <= n;i++)
	{
		cin >> w[i];
	}
	for (int i = 1;i <= n;i++) 
	{
		for (int j = m;j >= w[i];j--) 
		{
				if (f[j] < f[j - w[i]] + w[i])
				{
					f[j] = f[j - w[i]] + w[i];
				}
		}
	}
	cout << m - f[m];
	return 0;
}

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<algorithm>
using namespace std;
int n, x;
int const N = 1005;
int lose[N];
int win[N];
int use[N];
long long f[1005];
int main()
{
	cin >> n >> x;
	for (int i = 1;i <= n;i++)
	{
		cin >> lose[i] >> win[i] >> use[i];
	}
	for (int i = 1;i <= n;i++)
	{
		for (int j = x;j >= use[i];j--)
		{
			f[j] = max(f[j] + lose[i], f[j - use[i]] + win[i]);
		}
		for (int j = use[i] - 1;j >= 0;j--)
		{
			f[j] += lose[i];
		}
	}
	cout << f[x] * 5 << endl;
	return 0;
}