剑指offer—JZ10 斐波那契数列、JZ69 跳台阶

最新推荐文章于 2024-07-19 22:36:19 发布

牵猫散步的明

最新推荐文章于 2024-07-19 22:36:19 发布

阅读量253

点赞数 8

分类专栏：明与剑指Offer 文章标签：算法图论深度优先 c语言数据结构

本文链接：https://blog.csdn.net/weixin_72817878/article/details/128841587

版权

明与剑指Offer 专栏收录该内容

3 篇文章 0 订阅

订阅专栏

剑指offer—JZ10 斐波那契数列、JZ69 跳台阶

在这里插入图片描述
斐波那契数列，又称黄金分割数列，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……在数学上，斐波纳契数列以如下被以递归的方法定义：F（0）=0，F（1）=1，F（n）=F(n-1)+F(n-2)（n≥2，n∈N*），同样的类型的题还有兔子繁殖的问题。大同小异。
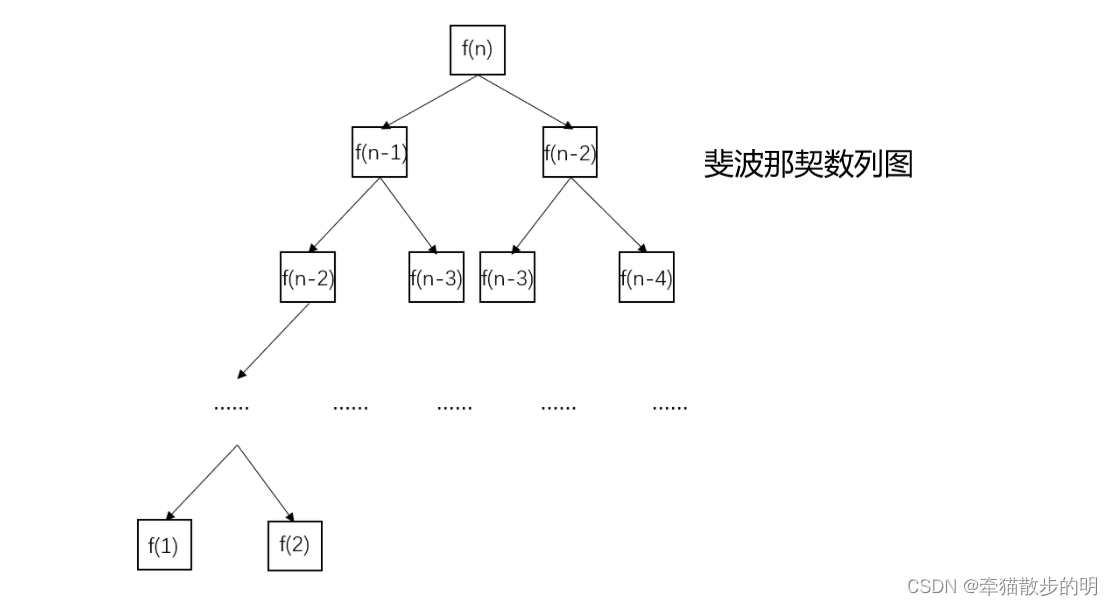
在这里插入图片描述

下面我们来谈及斐波那契数列的解决方法：

递归法

谈起斐波那契数列，相信大家一定绕不开递归这个方法，大部分读者第一次接触学习递归，都应该是用斐波那契数列来实现递归的，但递归虽然能实现斐波那契函数，但有一定的缺点。通过f[n] = f[n-1] + f[n-2], 初始值f[0]=0, f[1]=1这个公式可以直接将递归写出来：

int my_Fibonacci(int n)
{
	if (n < 3)
	{
		return 1;
	}
	else
	{
		return my_Fibonacci(n - 1)+ my_Fibonacci(n - 2);
	}
}
int main()
{
	int n = 0;
	while (scanf("%d", &n) != EOF)
	{
		int ret = 0;
		ret = my_Fibonacci(n);
		printf("所求的斐波那契数列的第%d项为：%d\n", n, ret);
	}
	return 0;
}

但此种方法过慢，会超时，时间复杂度是O(2^n)；空间复杂度是使用递归栈的空间。

时间复杂度 O(n)、空间复杂度O(1)的解法—动态规划法

用动态规划，优化掉递归栈空间。

int fib_n(int n)
{
    int dp[3] = {1, 1};
    if (n <= 1) return dp[n];

    for (int i = 2; i <= n; ++i)
        dp[i % 3] = dp[(i - 1) % 3] + dp[(i - 2) % 3];

    return dp[n % 3];
}

时间复杂度 O(logn) 、空间复杂度O(1)的解法

对于时间复杂度 O(logn) 的解法，我们可以思考一下下面的计算方式。

考虑一个求幂运算。比如求an，一般来说需要n次累乘，时间复杂度显然是O(n)。实际上可以通过递归达到一种更优化的效果：

an = (an/2)2 * an%2

这里的n/2是取整，如5/2=2。这样就可以实现相当于二分的效果，时间复杂度为O(logn)。

对于Fib数列an(n ≥ 0)，可以通过矩阵乘法的方式进行递推：
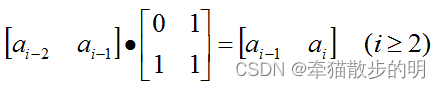
在这里插入图片描述
进而可以得到：

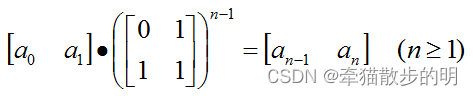
这样就可以把斐波那契数列问题转化成了一个求矩阵幂的运算问题。
结合以上思路，首先将其转化为矩阵求幂问题，然后进行二分，O(logn)解法由此诞生。

int** mult(int** m1, int** m2)
{
    int** res = new int*[2];
    for (int i = 0; i < 2; ++i) res[i] = new int[2];

    res[0][0] = m1[0][0] * m2[0][0] + m1[0][1] * m2[1][0];
    res[0][1] = m1[0][0] * m2[0][1] + m1[0][1] * m2[1][1];
    res[1][0] = m1[1][0] * m2[0][0] + m1[1][1] * m2[1][0];
    res[1][1] = m1[1][0] * m2[0][1] + m1[1][1] * m2[1][1];

    return res;
}

int** recur(int x)
{
    if (x == 0) {
        int** res = new int*[2];
        for (int i = 0; i < 2; ++i) res[i] = new int[2];
        res[0][0] = res[1][1] = 1;
        res[0][1] = res[1][0] = 0;
        return res;
    }
    if (x == 1) {
        int** res = new int*[2];
        for (int i = 0; i < 2; ++i) res[i] = new int[2];
        res[0][1] = res[1][0] = res[1][1] = 1;
        res[0][0] = 0;
        return res;
    }
    int** half = recur(x / 2);
    return mult(mult(half, half), recur(x % 2));
}

// time: O(logn)
int fib_logn(int n)
{
    if (n == 0 || n == 1) return 1;
    int** mat = recur(n - 1);
    return mat[0][1] + mat[1][1];
}

JZ69 跳台阶

在这里插入图片描述
从本质上而言，青蛙跳台阶也是斐波那契数列的问题。虽然他没有给出具体的公式而较为抽象，但经过总结后得出的公式规律是与斐波那契数列有很大的关系的。
首先，当N=1时，青蛙有一种跳法；

当N=2时，青蛙可以跳两次一级台阶，也可以跳一次二级台阶，则有两种跳法；

当N=3时，青蛙首先跳一次一级台阶，那么还剩两层的台阶，这时就是N=2时的跳法；青蛙跳一次二级台阶时，此时只剩一层台阶，这时就是N=1时的跳法，总结下来，此时的跳法就是（N=1）+（N=2）种跳法。

当N=4时，青蛙跳一次一级台阶时，还剩三层台阶，这时就是N=3时的跳法；青蛙跳一次二级台阶时，还剩二层台阶，这时就是N=2时的跳法；总结下来，此时的跳法就是（N=2）+（N=3）种跳法。

总而言之，当N>2时，就是前面两个的相加就得到青蛙跳台阶方法的总数，即符合斐波那契数列的数学特征，本质上第三个数只与前两个数有关。
归纳总结后，得到以下的数学表达式
在这里插入图片描述
既然如此，此题解的不同方式都可以与上述斐波那契数列的题解一一对齐，这边不多赘述，仅显现出一种简单的解法。

int my_Fibonacci(int number)
{
	int n1 = 1;int n2 = 2;
	if (number == 1)
	{
		return n1;
	}
	if (number == 2)
	{
		return n2;
	}
	for (int i = 3;i <= n;i++)
	{
		int temp = n2;
		n2 = n1 + n2;
		n1 = temp;
	}
	return n2;
}
int main()
{
	int n = 0;
	int ret = 0;
	while (scanf("%d", &n) != EOF)
	{
		ret = my_Fibonacci(n);
		printf("所求的斐波那契数列的第%d项为：%d\n", n, ret);
	}
	return 0;
}

方法一：迭代相加（推荐使用）

知识点：动态规划

动态规划算法的基本思想是：将待求解的问题分解成若干个相互联系的子问题，先求解子问题，然后从这些子问题的解得到原问题的解；对于重复出现的子问题，只在第一次遇到的时候对它进行求解，并把答案保存起来，让以后再次遇到时直接引用答案，不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果。本解法属于动态规划空间优化方法。
复杂度分析：
时间复杂度：O(n)，其中n为输入的数
空间复杂度：O(1)，常数级变量，没有其他空间。