【每日一题】【回溯+二进制优化】[USACO1.5] 八皇后 Checker Challenge C\C++\Java\Python3-CSDN博客

本文链接：https://blog.csdn.net/weixin_72899100/article/details/140714649

P1219 [USACO1.5] 八皇后 Checker Challenge

[USACO1.5] 八皇后 Checker Challenge

题目描述

一个如下的 $\times 6$ 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

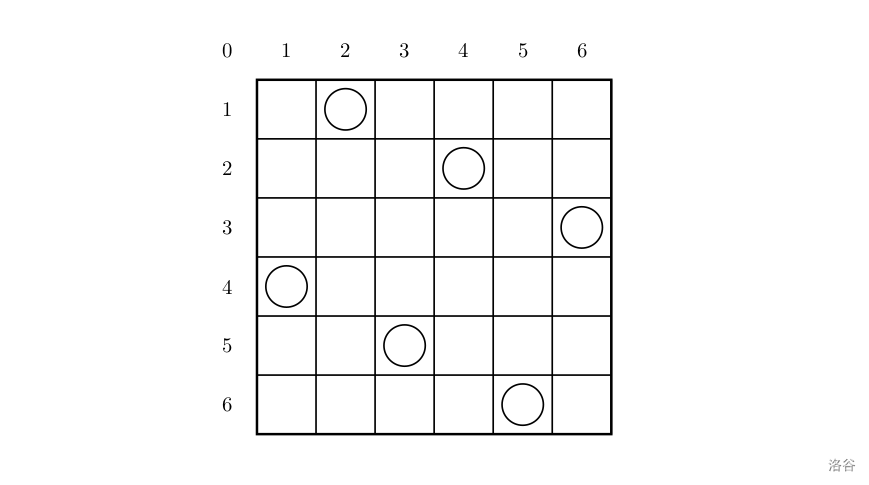
上面的布局可以用序列 $2\ 4\ 6\ 1\ 3\ 5$ 来描述，第 $i$ 个数字表示在第 $i$ 行的相应位置有一个棋子，如下：

行号 $1\ 2\ 3\ 4\ 5\ 6$

列号 $2\ 4\ 6\ 1\ 3\ 5$

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 $3$ 个解。最后一行是解的总个数。

输入格式

一行一个正整数 $n$ ，表示棋盘是 $\times n$ 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

样例 #1

样例输入 #1

样例输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

提示

【数据范围】
对于 $100\%$ 的数据， $\le n \le 13$ 。

题目翻译来自NOCOW。

USACO Training Section 1.5

做题要点

字典顺序排列
$\le n \le 13$
输出前 $3$ 个解
每行、每列有且只有一个棋子，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。
以上面的序列方法输出(题目给出了具体的答案输出规则)

做题思路

因为每行、每列有且只有一个棋子，那么模拟放棋子的情况。
因为答案是行号按顺序的，所以按行(从第一行放到第 $n$ 行可以满足题目序列方法输出要求)来依次放棋子是合理的。那么顺序为先行后列。

看一个普遍的情况，假设到了第 $m$ 行，行数固定了，那么看该行上每一列(也是从第一列开始到最后一列)的情况。
假设考虑到了第 $m$ 行 $k$ 列，首先应该判断该位置能不能放棋子:

如果可以那么将其放下，然后考虑第 $m + 1$ 行 $1$ 列(因为该行已经放了棋子了，所以考虑下一行)。
如果不可以那么往后走，如果 $k + 1$ 不等于 $n$ 的话，考虑第 $m$ 行 $k + 1$ 列；否则，考虑第 $m + 1$ 行 $1$ 列
重复以上步骤直到走完整个棋盘，然后判断棋盘上是否有 $n$ 枚棋子，如果有记为其中一种情况，否则不计入。

到这里已经有第一个答案了
由于题目要求字典顺序排列，就要考虑第二个答案和第一个答案之间的关系。

最粗暴(简单但吃速度)的做法为从新来一遍，直到走完整个棋盘，然后判断棋盘上是否有 $n$ 枚棋子且不为第一个答案(已有答案)，那么就记为第二个答案，否则不计入。
然后以此类推得出三个答案…直到所有答案或再用其他办法跑出解的总个数。

字典顺序排列其实就是首先看第一个字符比较大小，如果相等比较下一个字符，否则大的为大。
那么按照字典序的思想，应该先改变最后一个字符(变大),也就是最后一行棋子的列数变大。
如果无法改变把最后一个字符变大，那么就把最后一个字符变最小，改变倒数第二个字符。
依次类推。即字典序逐步增大。

那么第一次走完整个棋盘后，拿掉最后一个棋子(也就是最后一行的棋子,假设原本在第 $m$ 行 $k$ 列)，然后考虑第第 $m$ 行 $k + 1$ 列能不能放棋子，回到上述步骤。
这里就出现了一个新问题和老问题，如果棋盘上没有 $n$ 枚棋子或者该行无法放棋子了，怎么办？
也就说出现了至少有一行无法放下棋子。这说明放该行以前就把该行的所有情况ban掉了(无法放了)。
换句话说以前放的棋子策略是错的。
那么就需要从新放以前的棋子，再加上字典序的思想。首先调整的就是不能放棋子的那行的上一行。
按照这样的调整思路，如果不能放那就往回走，如果放满了自然就是一种情况，并且答案是按照字典序排序的。

将这种思想称为回溯.

接着说说如何判断该位置能不能放棋子。
最直接的操作，行、列、副对角线、主对角线各一个标记数组。
记为 $row , column,Sub\_ diagonal, Main\_ diagonal$ ;
其中 $row_i = true$ 表示第 $i$ 行可以放，否则不行。
同理， $column_i = true$ 表示第 $i$ 列可以放，否则不行。
那么主副对角线需要找到对应关系。
这里直接给出。
同一副对角线上的格子，下标相加相等，例如第一行第二列和第二行第一列，加起来都为3
同一主对角线上的格子，下标相减相等
例如第一行第四列和第三行第六列， $1 - 4 = 3 - 6 = - 3$
因为会出现负数，在程序中可以加上 $n$ 即可全为正数，对数组访问更方便。

二进制优化

对于判断该位置能不能放棋子的操作可以进行二进制优化。
可以优化空间复杂度
可以看到 $\le n \le 13$ ，也就是说 $n$ 不大，那么开出来的四个标记数组也不大。
如果换成一个数字，其中二进制的每一位都为一个标记，那么空间复杂度从一个数组变成一个数字了。

例如二进制数字 $0001000$ 对应的数组应该是 $v [4] = t r u e$ 其他全为 $f a l se$ 类似这种对应关系。
如果要进行 $v [3] = t r u e$ 则对二进制数字对应位或(|) 上1即可，最终变为 $0001100$

总结思路：

假设考虑到了第 $m$ 行 $k$ 列，首先应该判断该位置能不能放棋子:

如果可以那么将其放下，如果 $m + 1 == n$ 记为一种情况(棋盘放满了),将其拿去,继续考虑第 $m$ 行 $k + 1$ 列的情况( $k + 1 == n$ 的话,拿去 $m - 1$ 行的棋子(记为 $a$ 列),继续考虑第 $m - 1$ 行 $a + 1$ 列);否则,考虑第 $m + 1$ 行 $1$ 列(因为该行已经放了棋子了，所以考虑下一行)。
如果不可以那么往后走，如果 $k + 1$ 不等于 $n$ 的话，考虑第 $m$ 行 $k + 1$ 列；否则，进入第三个情况。
回到 $m - 1$ 行有棋子的那一列(假设为 $a$ 列)，将该棋子拿去，如果 $a + 1$ 不等于 $n$ 的话,继续考虑第 $m - 1$ 行 $a + 1$ 列，否则,考虑第 $m - 1$ 行 $a$ 列的第三种情况.
重复以上过程直到回跳到了第 $0$ 行(棋盘外面).

时间复杂度分析

首先分析最简单的第一个棋子如果放在第一行 $n$ 种情况，到最后一个棋子肯定只有一种情况了。因为涉及到主对角线和副对角线的剪枝问题，该时间复杂度无法很好推出。
退一步，如果不考虑主对角线和副对角线的情况，那么该时间复杂度应该是 $O (n!)$ 。
在先如果考虑的话，第 $k$ 行可能减少 $k_1$ 个情况
那么时间复杂度 $\displaystyle\sum_{i=1}^{n} k_i)$
但粗略分析，时间复杂度随 $n$ 的增大，后续会迅速增大(可能为指数增长或者低于 $n$ 倍高于 $n - 3$ 倍增长)
具体跑程序分析可得下图
在这里插入图片描述

伪代码

在这里插入图片描述

核心代码对应思路

void Solution::dfs(int x){
    if(x == n+1){//棋盘被放满
        cnt++;//答案情况+1
        if(cnt <= 3) {//如果是前三个答案
            for (auto i: ans)//输出答案
                std::cout << i << ' ';
            std::cout << "\n";
            //return; //(可选)
        }
    }
    for(int y=1;y<=n;y++){//枚举每一列
        if(check(x,y)){//判断该位置能不能放棋子
            put_down(x,y);//放棋子，做标记
            dfs(x+1);//到下一行
            pick_up(x,y);//拿掉棋子，去掉标记
        }
    }
    //y == n+1 一行都放不下了进入第三个情况，回退到上一个dfs(x-1)
}

假设考虑到了第 $m$ 行 $k$ 列，首先应该判断该位置能不能放棋子:

如果可以那么将其放下，如果 $m + 1 == n$ 记为一种情况(棋盘放满了),将其拿去,继续考虑第 $m$ 行 $k + 1$ 列的情况( $k + 1 == n$ 的话,拿去 $m - 1$ 行的棋子(记为 $a$ 列),继续考虑第 $m - 1$ 行 $a + 1$ 列);否则,考虑第 $m + 1$ 行 $1$ 列(因为该行已经放了棋子了，所以考虑下一行)。
如果不可以那么往后走，如果 $k + 1$ 不等于 $n$ 的话，考虑第 $m$ 行 $k + 1$ 列；否则，进入第三个情况。
回到 $m - 1$ 行有棋子的那一列(假设为 $a$ 列)，将该棋子拿去，如果 $a + 1$ 不等于 $n$ 的话,继续考虑第 $m - 1$ 行 $a + 1$ 列，否则,考虑第 $m - 1$ 行 $a$ 列的第三种情况.
重复以上过程直到回跳到了第 $0$ 行(棋盘外面).

return;是可选的原因为，放满 $n$ 个棋子后必定无法放 $n + 1$ 个棋子了。
所以不写return递归也肯定无法继续深入。
注:回溯写return出口是比较好的习惯

完整代码

#include <stdio.h>
#define re(i) (1<<(i))
const int N = 1e5;
int cnt , n , ans[20];
long long row,column,Sub_diagonal,Main_diagonal;
void dfs(int x){
    if(x == n+1){
        cnt++;
        if(cnt <= 3)
            for(int i=1;i<=n;i++)printf("%d%c",ans[i]," \n"[n==i]);
        return ;
    }
    for(int i=1;i<=n;i++){
        //二进制优化
        if((row&re(x)) || (column&re(i)) || (Sub_diagonal&re(i+x)) || (Main_diagonal&re(i-x+n)));
        else{
            row|=re(x);column|=re(i);Sub_diagonal|=re(i+x);Main_diagonal|=re(i-x+n);
            ans[x]=i;
            dfs(x+1);
            row^=re(x);column^=re(i);Sub_diagonal^=re(i+x);Main_diagonal^=re(i-x+n);
        }
    }
}
void init(){
    NULL;
}
int main() {
    scanf("%d",&n);
    init();
    dfs(1);
    printf("%d",cnt);
    return 0;
}

C++

#include <iostream>
#include <vector>
#include <cstring>
class Solution{
    int n,cnt;
    bool *row , *column;
    bool *Sub_diagonal,*Main_diagonal;
    std::vector<int>ans;
    void dfs(int x);
    void init();
    inline bool check(int ,int );
    inline void put_down(int,int);
    inline void pick_up(int,int);
public:
    void solve();
};
int main() {
    auto *solution = new Solution();
    solution->solve();
    return 0;
}
void Solution::dfs(int x){
    if(x == n+1){
        cnt++;
        if(cnt <= 3) {
            for (auto i: ans)
                std::cout << i << ' ';
            std::cout << "\n";
        }
    }
    for(int y=1;y<=n;y++){
        if(check(x,y)){
            put_down(x,y);
            dfs(x+1);
            pick_up(x,y);
        }
    }
}
inline bool Solution::check(int x,int y){
    return row[x] && column[y] && Sub_diagonal[x+y] && Main_diagonal[x-y+n];
}
void Solution::init() {
    std::cin >> n;
    row = new bool[n+1];memset(row,true,n+1);
    column = new bool[n+1];memset(column,true,n+1);
    Sub_diagonal = new bool[(n<<1)+1];memset(Sub_diagonal,true,(n<<1) + 1);
    Main_diagonal = new bool[n<<1];memset(Main_diagonal,true,n<<1);
    cnt = 0;
    ans.clear();
}
void Solution::solve() {
    init();
    dfs(1);
    std::cout << cnt ;
}
inline void Solution::put_down(int x, int y) {
    ans.push_back(y);
    row[x] ^= true;
    column[y] ^= true;
    Sub_diagonal[x+y] ^= true;
    Main_diagonal[x-y+n] ^= true;
}
inline void Solution::pick_up(int x, int y) {
    ans.pop_back();
    row[x] |= true;
    column[y] |= true;
    Sub_diagonal[x+y] |= true;
    Main_diagonal[x-y+n] |= true;
}

Java

import java.util.Scanner;
import java.util.Vector;

public class Main {
    static int n,cnt;
    static boolean[] row =new boolean[100];
    static boolean[] column =new boolean[100];
    static boolean[] Sub_diagonal =new boolean[100];
    static boolean[] Main_diagonal =new boolean[100];
    static Vector<Integer>v = new Vector<>();

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        init();
        dfs(1);
        System.out.print(cnt);
    }

    public static void dfs(int x){
        if(x == n+1){
            cnt++;
            if(cnt <= 3){
                for(Integer i:v){
                    System.out.print(i + " ");
                }
                System.out.println();
            }
            return ;
        }
        for(int i=1;i<=n;i++){
            if(check(x,i)){
                put_down(x,i);
                dfs(x+1);
                pick_up(x,i);
            }
        }
    }
    public static void init(){
        cnt = 0;
        for(int i=1;i<100;i++){
            row[i] = column[i] = Sub_diagonal[i] = Main_diagonal[i] = true;
        }
    }
    public static boolean check(int x,int y){
        return row[x] && column[y] && Sub_diagonal[x+y] && Main_diagonal[x-y+n];
    }
    public static void put_down(int x,int y){
        v.add(y);
        row[x] ^= true;
        column[y] ^= true;
        Sub_diagonal[x+y] ^= true;
        Main_diagonal[x-y+n] ^= true;
    }
    public static void pick_up(int x,int y){
        v.removeLast();
        row[x] ^= true;
        column[y] ^= true;
        Sub_diagonal[x + y] ^= true;
        Main_diagonal[x - y + n] ^= true;
    }
}

Python3(不推荐)
因为最后一个点需要打表才能过

n = int(input())
row = [0 for i in range(200)]
column = [0 for i in range(200)]
Sub_diagonal  = [0 for i in range(200)]
Main_diagonal = [0 for i in range(200)]
cnt = 0

def printf():
    global cnt
    for i in range(1,n+1):
        print(row[i], end=' ')
    print()
def dfs(x):
   global cnt
   if x == n+1:
       cnt=cnt+1
       if cnt <= 3:
            printf()
       return
   for y in range(1,n+1):
       if column[y] == 0 and Sub_diagonal[x+y] == 0 and Main_diagonal[x-y+n] == 0:
           row[x] = y
           column[y] = 1
           Sub_diagonal[x+y] = 1
           Main_diagonal[x-y+n] = 1
           dfs(x+1)
           column[y] = 0
           Sub_diagonal[x+y] = 0
           Main_diagonal[x-y+n] = 0

if n==13:
    print('1 3 5 2 9 12 10 13 4 6 8 11 7')
    print('1 3 5 7 9 11 13 2 4 6 8 10 12')
    print('1 3 5 7 12 10 13 6 4 2 8 11 9')
    print(73712)
    exit(0)
dfs(1)
print(cnt)