MachileLearn/机器学习
标准符号/Standard Notation：
Training set: data used to train the modle(训练集)
lowercase x = Input / Feature / Input Feature(小写x)
lowercase y = Output/ Target(小写y)
lowercase m = Number of training examples(小写m)
parentheses(x,y) = single training example( ( x , y ) (x,y) (x,y)表示一个例子)
superscript:上标 x ( i ) x^{(i)} x(i)
subscript:下标 x j x_j xj
y
^
(
i
)
:
y
−
h
a
t
y
的预测值
y
(
i
)
:
y
的真实值
\hat{y}^{(i)}:y-hat\quad y的预测值\\ y^{(i)}:y的真实值
y^(i):y−haty的预测值y(i):y的真实值
f w → , b ( x → ) = P ( y = 1 ∣ x → ; w → , b ) f_{\overrightarrow{\mathrm{w}}, b}(\overrightarrow{\mathrm{x}})=P(y=1 \mid \overrightarrow{\mathrm{x}} ; \overrightarrow{\mathrm{w}}, b) fw,b(x)=P(y=1∣x;w,b)：x是input,w,b是参数
y=1是概率
underfitting / 欠拟合：模型无法契合数据
generalization /泛化：对于未给出的数据，拟合程度也很好
1.Supervised Learning/监督学习
（1）定义：
给算法一个数据集其中包含了正确的答案，算法的目的是给出更多的正确答案。
learn inputs ,outputs or x to y mappings
（2）Regression/回归
回归问题目的： 预测连续的数值输出
predict numbers out of infinitely many possible numbers
回归的应用：
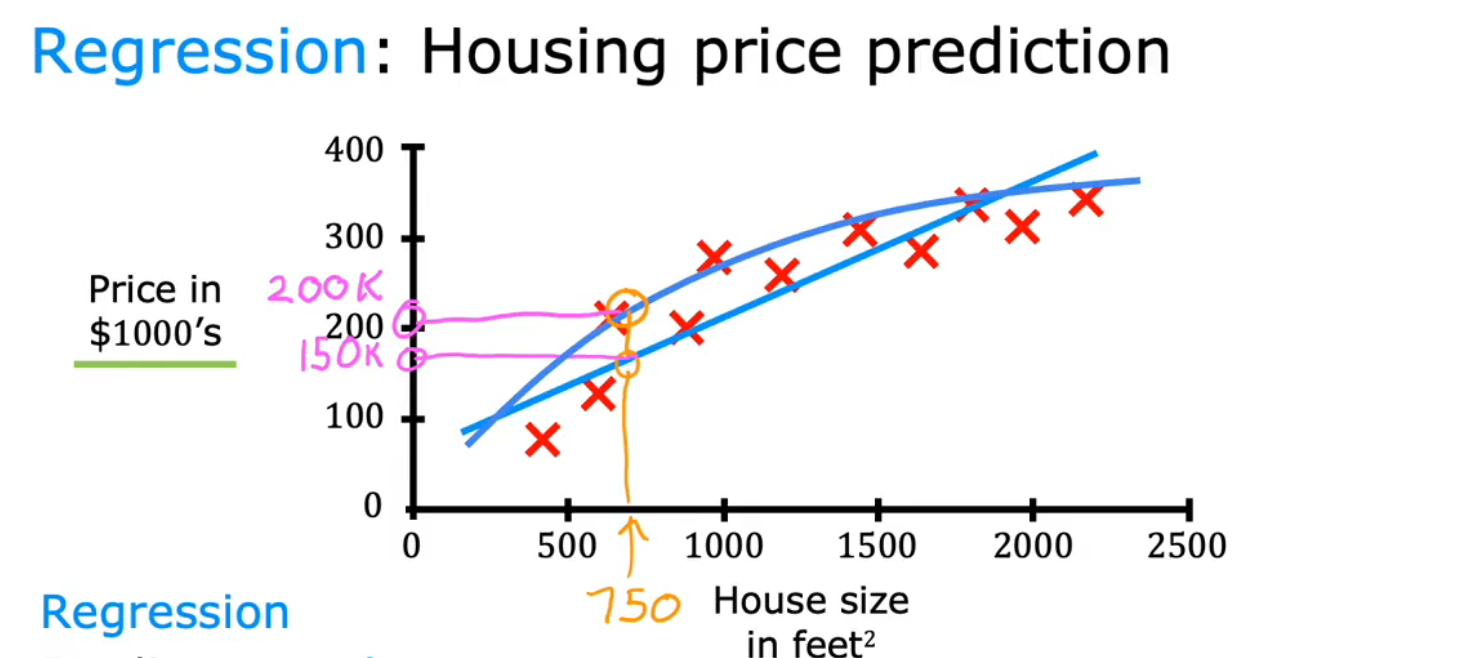
例：Housing price prediction/房价预测
①用直线拟合
②用曲线拟合
（3）classification/分类
分类的目的：找到边界
find some boundary that separates out A from B
decide how to fit a boundary line through this data
例：Breast cancer detection/乳腺癌检测
2.Unsupervised Learning/无监督学习
（1）定义：
给算法一个数据集，但是不给数据集的正确答案，由算法自行分类。
find something interesting in unlabeled data
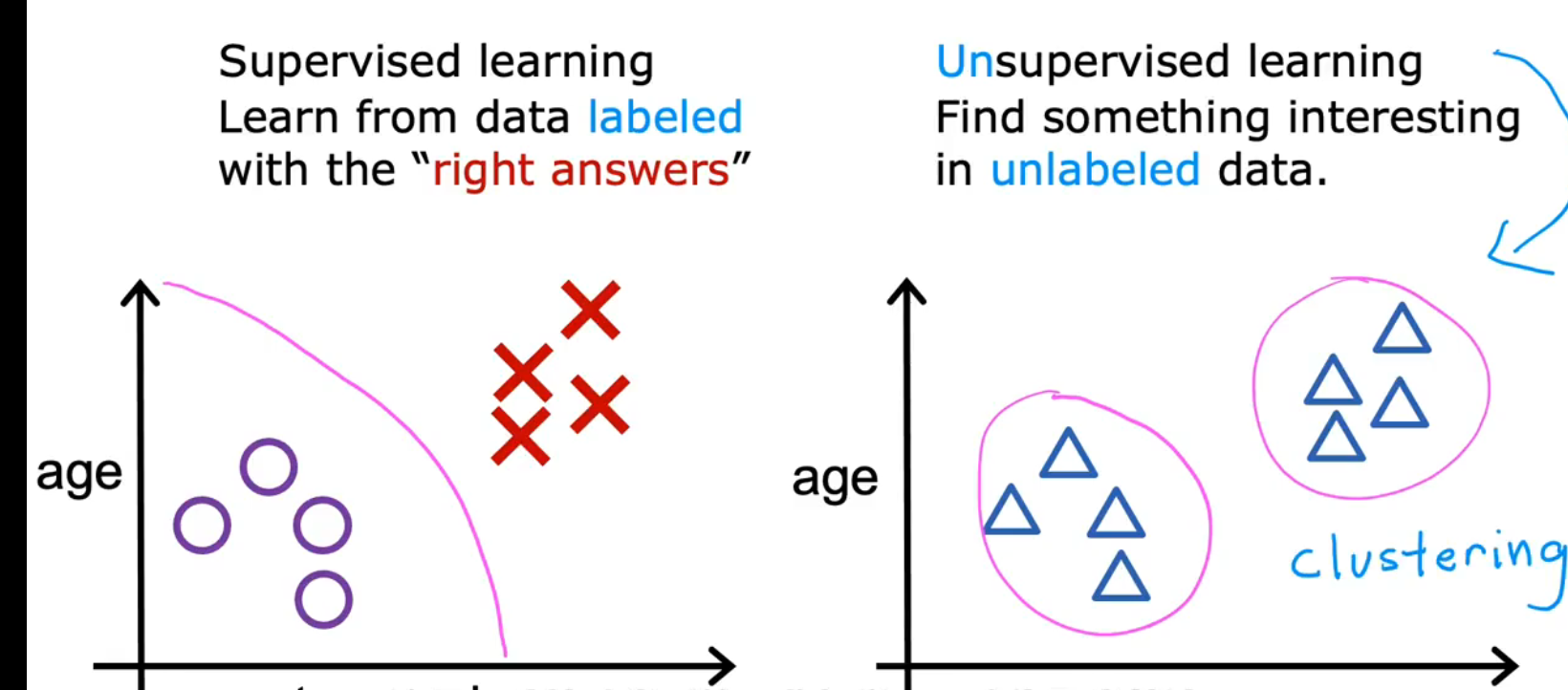
only input X, not output Y
（2）Clustering algorithm/聚类算法
例1：
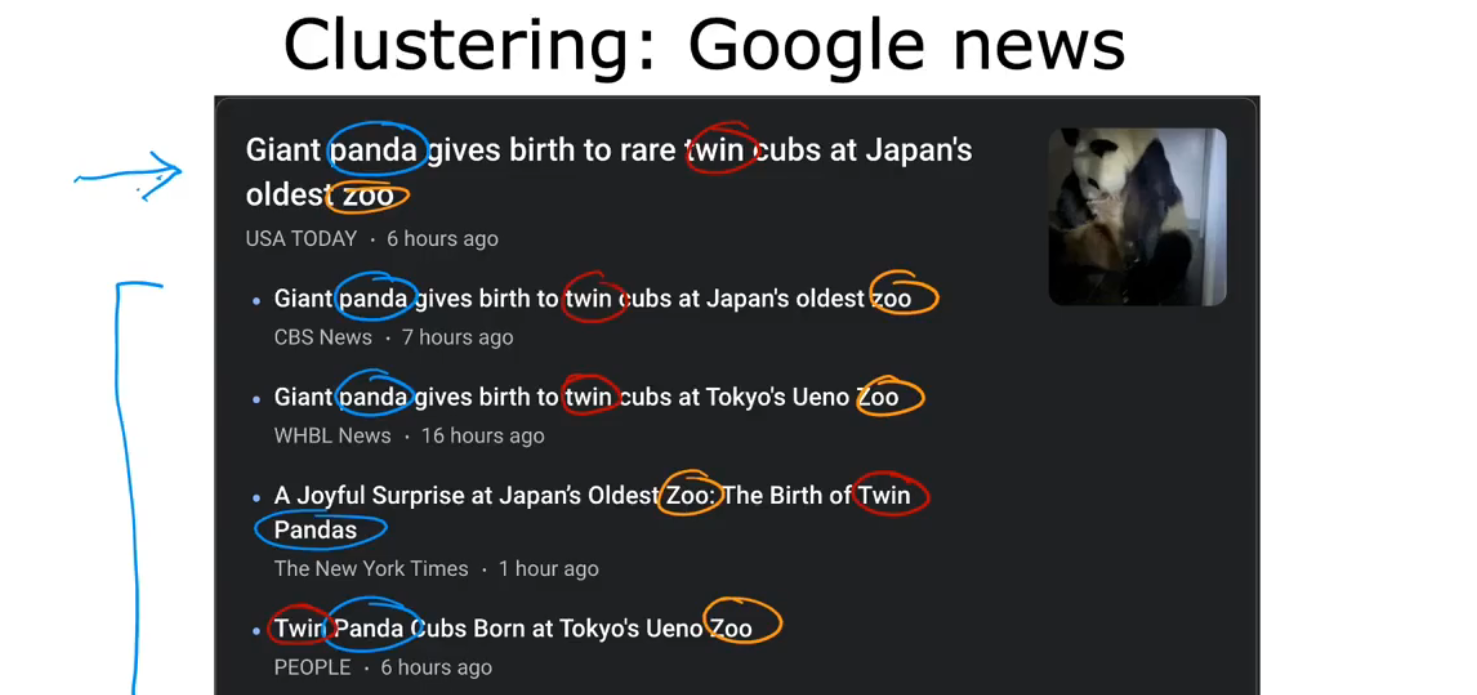
3.Linear Regression/线性回归
Univariate linear refression：单变量线性回归
f(x)=wx+b
w:weight b:bais
4.Cost Function/代价函数
（1）定义：
衡量一条直线与训练数据的拟合程度
目的:Minimize J(w,b)
（2）形式：
计算平均平方误差（为了构建一个不会随着训练集大小变大而自动变大的成本函数）(按照惯例，要除以2m，2只是为了之后的计算更加整洁，无论是否包含2，成本函数仍然有效)
平方误差成本函数：Squared error cost function
J
(
w
,
b
)
=
1
2
m
∑
i
=
1
m
(
y
^
(
i
)
−
y
(
i
)
)
(
2
)
J
(
w
,
b
)
=
1
2
m
∑
i
=
1
m
(
f
w
,
x
(
x
(
i
)
)
−
y
(
i
)
)
(
2
)
m=number of training examples
J(w,b)=\frac{1}{2m}\sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)})^{(2)}\\ J(w,b)=\frac{1}{2m}\sum_{i=1}^{m}(f_{w,x}(x^{(i)})-y^{(i)})^{(2)}\\ \text{m=number of training examples }
J(w,b)=2m1i=1∑m(y^(i)−y(i))(2)J(w,b)=2m1i=1∑m(fw,x(x(i))−y(i))(2)m=number of training examples
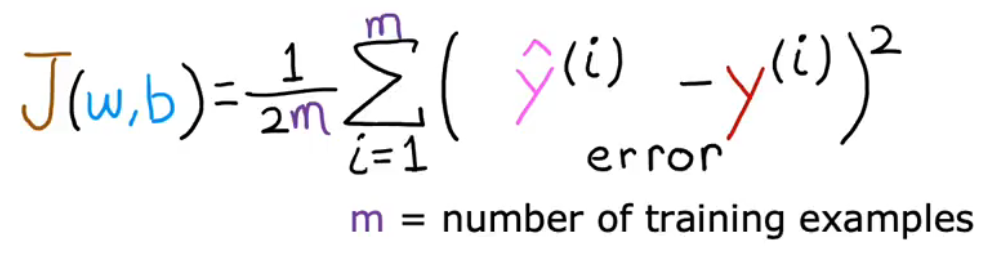
（3）只有weight，没有bais
f w ( x ) = w x , x ∈ { 1 , 2 , 3 } J ( w ) = 1 2 m ∑ i = 1 m ( f w ( x ( i ) ) − y ( i ) ) 2 f_{w}(x)=wx,\quad x \in \{1,2,3\} \\ J(w)=\frac{1}{2m}\sum_{i=1}^{m}(f_{w}(x^{(i)})-y^{(i)})^2 fw(x)=wx,x∈{1,2,3}J(w)=2m1i=1∑m(fw(x(i))−y(i))2
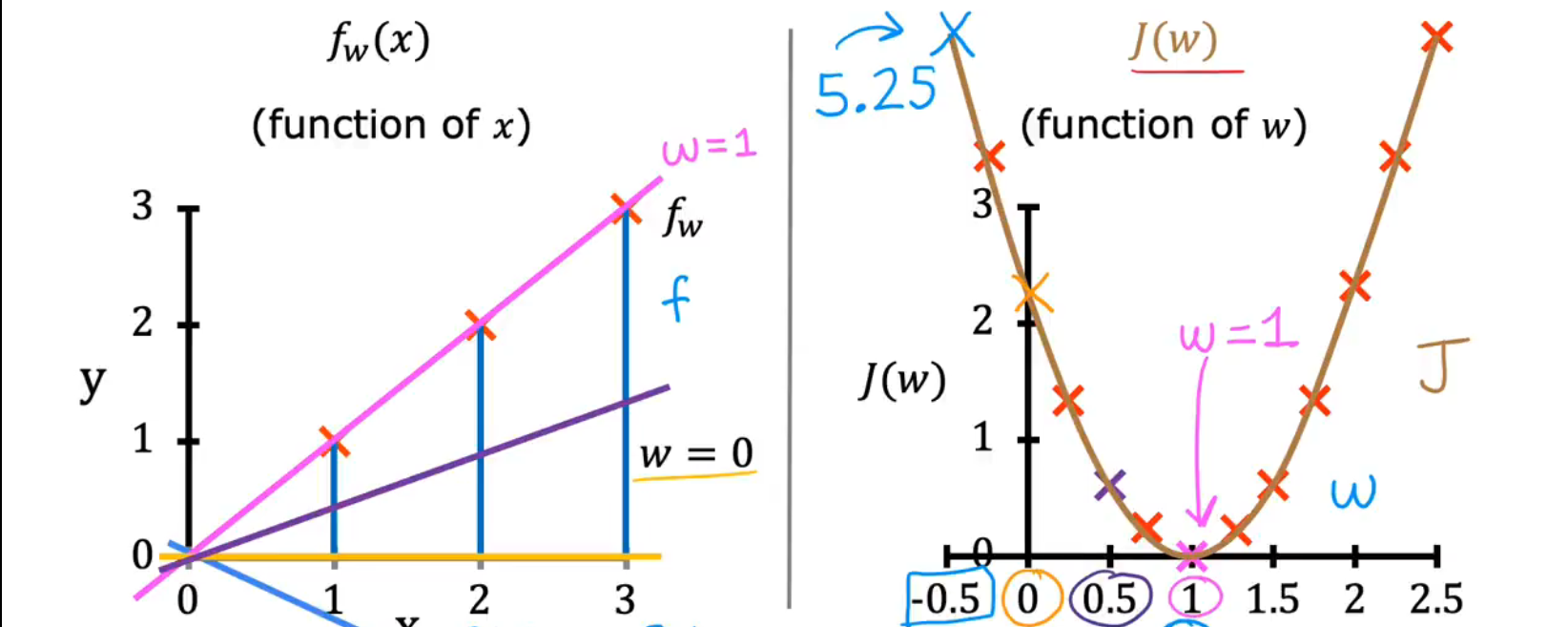
（4）weight 和bais
f w , b ( x ) = 0.06 x + 50 f_{w, b}(x)=0.06 x+50 fw,b(x)=0.06x+50
J(w,b)变成了三维图像
也可以是二维的图像，类似于等高线
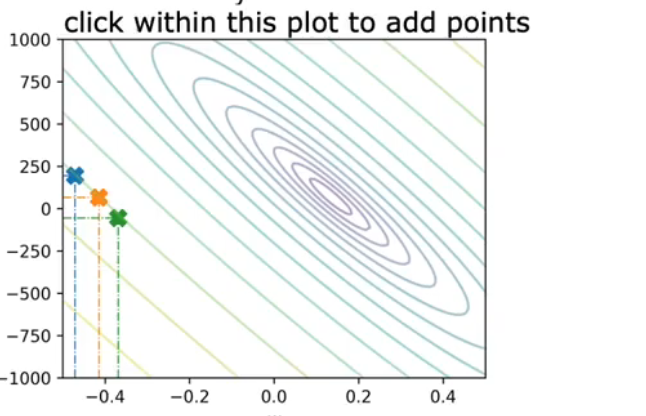
5.Gradient Descent/梯度下降
（1）定义：
最小化任何函数 minimize any function not only cost function for linear function
（2）Outline:
- Start with some w,b(w,b可以是任意设置的，但是一般设置为0开始)
- Keep changing w,b to reduce J(w,b)
- Util we settle at or near a minimum
注意 : function not only has one minimum
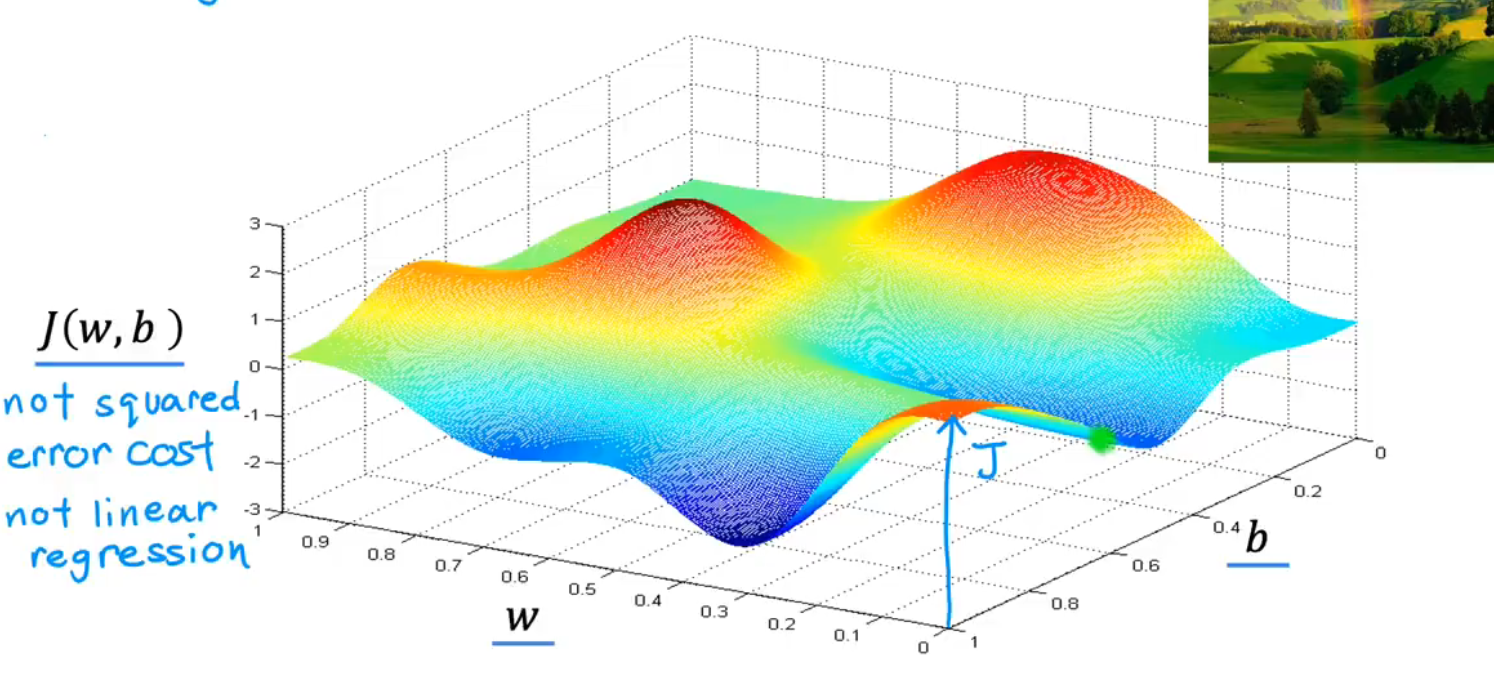
the direction of steepest descent:最速下降的方向
（3）local minimun:局部最优解
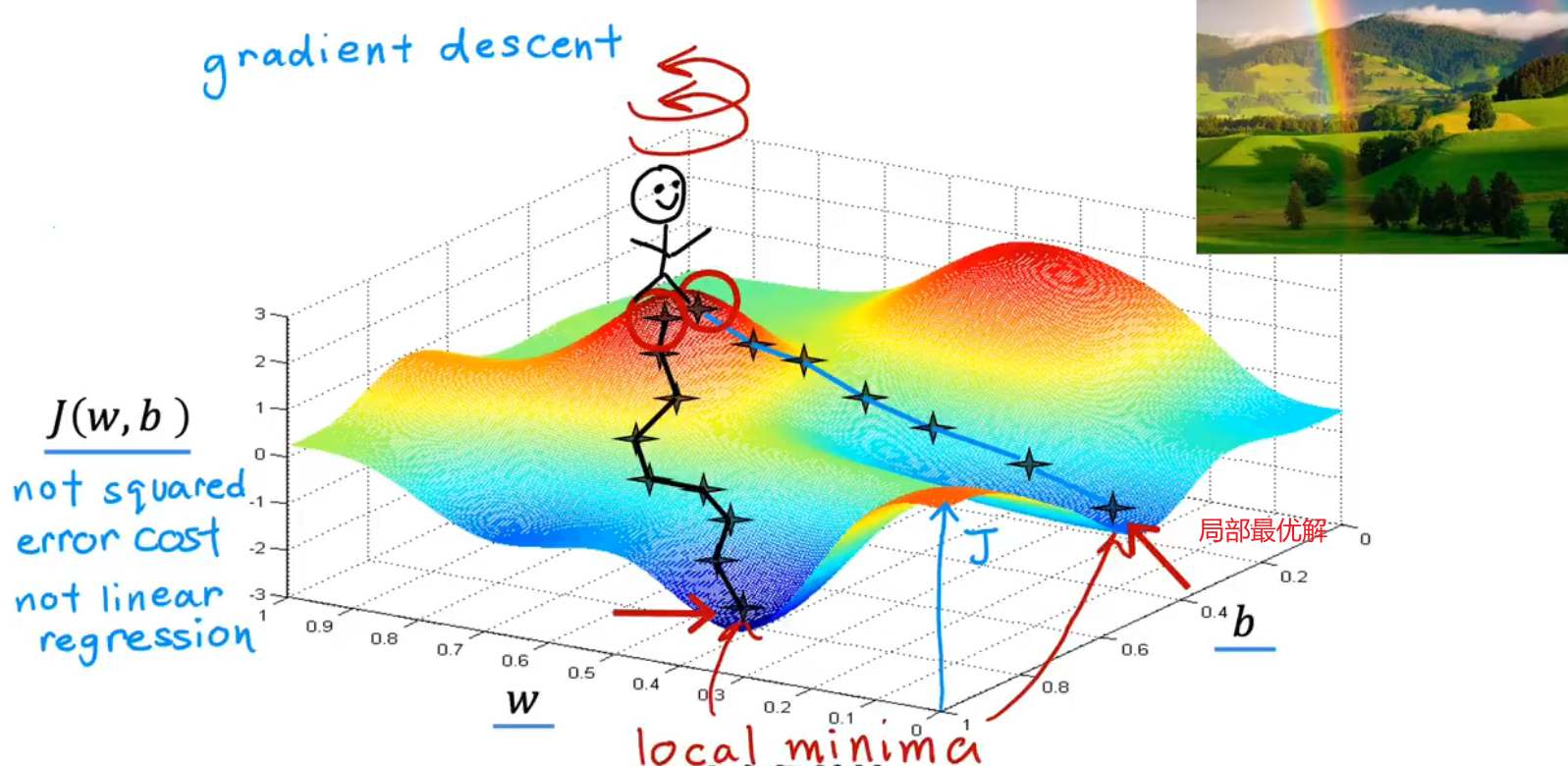
对于不同的起始位置(w,b)，最速下降的方向也是不同的，得到的局部最优解local minimum也是不同的
（4）Implement/实现
ω = ω − α ∂ ∂ ω J ( w , b ) b = b − α ∂ ∂ b J ( ω , b ) ∂ ∂ b J ( ω , b ) ∂ ∂ ω J ( w , b ) 是J(w,b)的导数项 \omega=\omega-\alpha \frac{\partial}{\partial \omega} J(w, b)\\ b=b-\alpha \frac{\partial}{\partial b} J(\omega, b)\\ \frac{\partial}{\partial b} J(\omega, b)\quad \frac{\partial}{\partial \omega} J(w, b)\text{是J(w,b)的导数项} ω=ω−α∂ω∂J(w,b)b=b−α∂b∂J(ω,b)∂b∂J(ω,b)∂ω∂J(w,b)是J(w,b)的导数项
α：Learning rate 学习率（通常是0~1之间的一个小正数，控制下降的幅度
正确的同步更新：
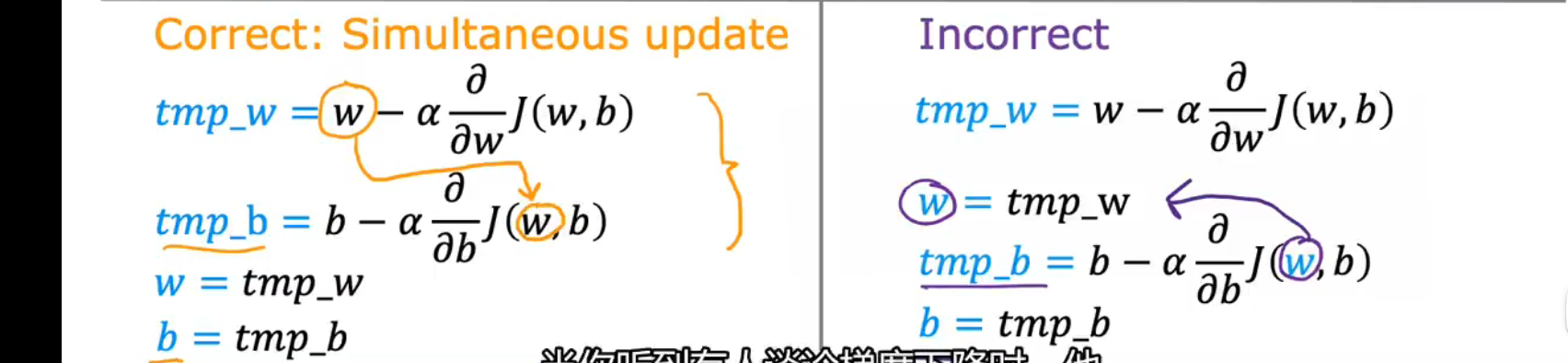w,b必须要同步更新，
tmp_b中的ω是更新之前的ω，不是被tmp_ω更新后的ω
6.Learning Rate/学习率
（1）学习率 too samll:
更新的太慢
（2）学习率 too big :
跟新的幅度太大，可能永远也不会到达minimum，或者无法收敛，直接发散
（3）Local minimum局部最优解
J ( w , b ) J(w,b) J(w,b)到达局部最优解 \ local minimum
随着导数的大小的减小，每一次下降的幅度也在减小，直到导数变为0，此时不再移动。
所以，这个公式可以到达local minimum,而不用减小学习率
（4）Global minimum全局最优解
成本函数J所具有的最低可能的值
7.用于线性回归的梯度下降
(1)公式的推导
导数项的推导：
∂
∂
w
J
(
w
,
b
)
=
∂
∂
w
1
2
m
∑
i
=
1
m
(
f
w
,
b
(
x
(
i
)
)
−
y
(
i
)
)
2
=
d
d
w
1
2
m
∑
i
=
1
m
(
w
x
(
i
)
+
b
−
y
(
i
)
)
2
=
1
2
m
∑
i
=
1
m
(
w
x
(
i
)
+
b
−
y
(
i
)
)
2
x
(
i
)
\frac{\partial}{\partial w} J(w, b)\\ = \frac{\partial}{\partial w} \frac{1}{2 m} \sum_{i=1}^m\left(f_{w, b}\left(x^{(i)}\right)-y^{(i)}\right)^2\\ =\frac{d}{d w} \frac{1}{2 m} \sum_{i=1}^m\left(w x^{(i)}+b-y^{(i)}\right)^2 \\ =\frac{1}{2 m} \sum_{i=1}^m\left(w x^{(i)}+b-y^{(i)}\right) 2 x^{(i)}
∂w∂J(w,b)=∂w∂2m1i=1∑m(fw,b(x(i))−y(i))2=dwd2m1i=1∑m(wx(i)+b−y(i))2=2m1i=1∑m(wx(i)+b−y(i))2x(i)
导数项：
d
∂
w
J
(
w
,
b
)
=
1
m
∑
i
=
1
m
(
f
w
,
b
(
x
(
i
)
)
−
y
(
i
)
)
x
(
i
)
d
∂
b
J
(
w
,
b
)
=
1
m
∑
i
=
1
m
(
f
w
,
b
(
x
(
i
)
)
−
y
(
i
)
)
\frac{d}{\partial w} J(w, b)=\frac{1}{m} \sum_{i=1}^m\left(f_{w, b}\left(x^{(i)}\right)-y^{(i)}\right) x^{(i)}\\ \frac{d}{\partial b} J(w, b)=\frac{1}{m} \sum_{i=1}^m\left(f_{w, b}\left(x^{(i)}\right)-y^{(i)}\right)
∂wdJ(w,b)=m1i=1∑m(fw,b(x(i))−y(i))x(i)∂bdJ(w,b)=m1i=1∑m(fw,b(x(i))−y(i))
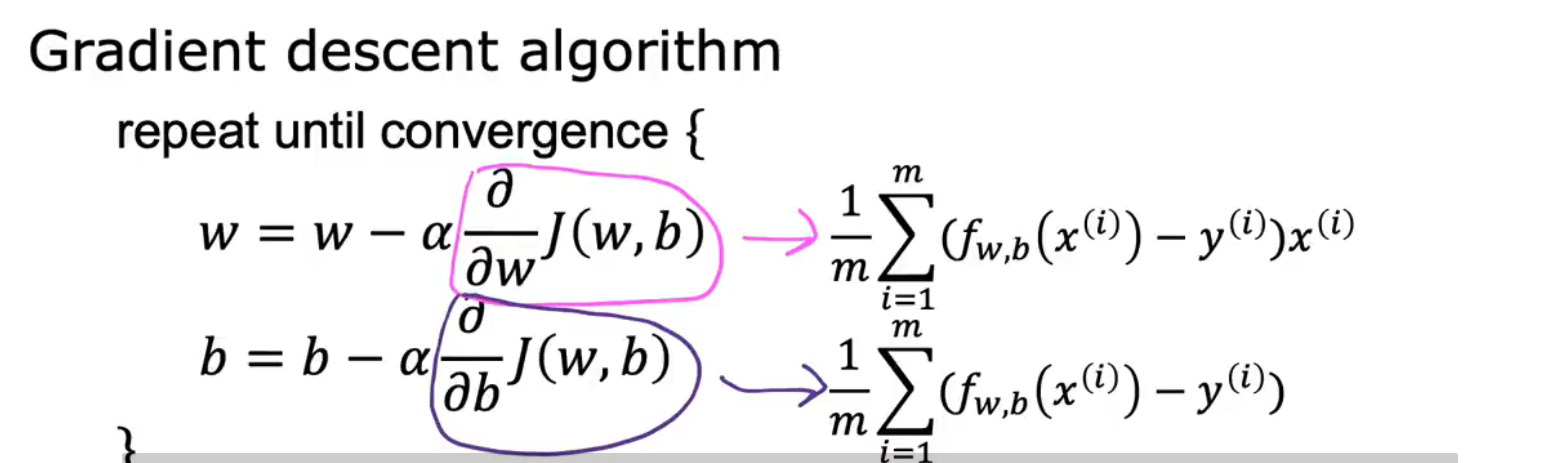
将导数项带入式子中得到：
ω
=
ω
−
α
1
m
∑
i
=
1
m
(
f
w
,
b
(
x
(
i
)
)
−
y
(
i
)
)
x
(
i
)
b
=
b
−
α
1
m
∑
i
=
1
m
(
f
w
,
b
(
x
(
i
)
)
−
y
(
i
)
)
\omega=\omega-\alpha \frac{1}{m} \sum_{i=1}^m\left(f_{w, b}\left(x^{(i)}\right)-y^{(i)}\right) x^{(i)}\\ b=b-\alpha \frac{1}{m} \sum_{i=1}^m\left(f_{w, b}\left(x^{(i)}\right)-y^{(i)}\right)
ω=ω−αm1i=1∑m(fw,b(x(i))−y(i))x(i)b=b−αm1i=1∑m(fw,b(x(i))−y(i))
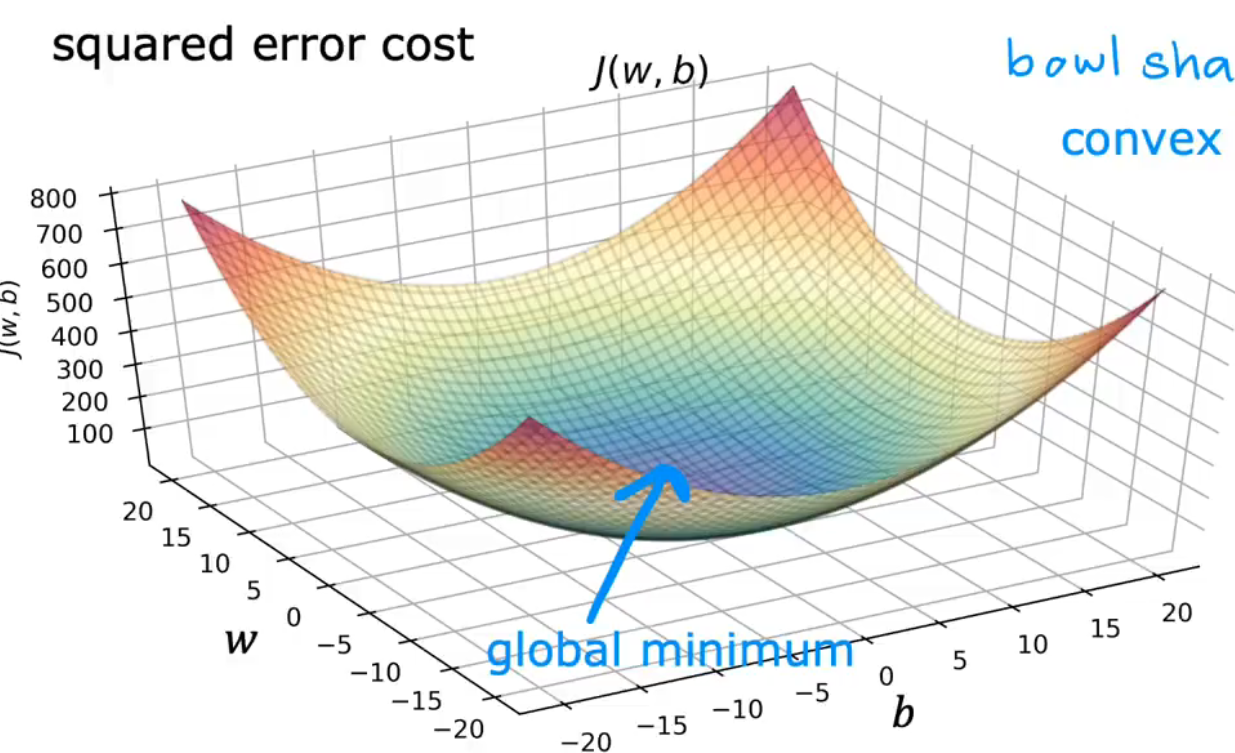
(2)为什么用平方误差成本函数
以及关于局部/全局最优解的讨论
平方误差成本函数/squared error cost function是一个凹函数/碗型函数，所以只有一个极值/最值
当cost function使用平方误差成本函数时，cost function永远不会有多个local minimum,而是只有一个local minumum,这个局部最优解就是函数的全局最优解 global minimum。
(3)运行梯度下降
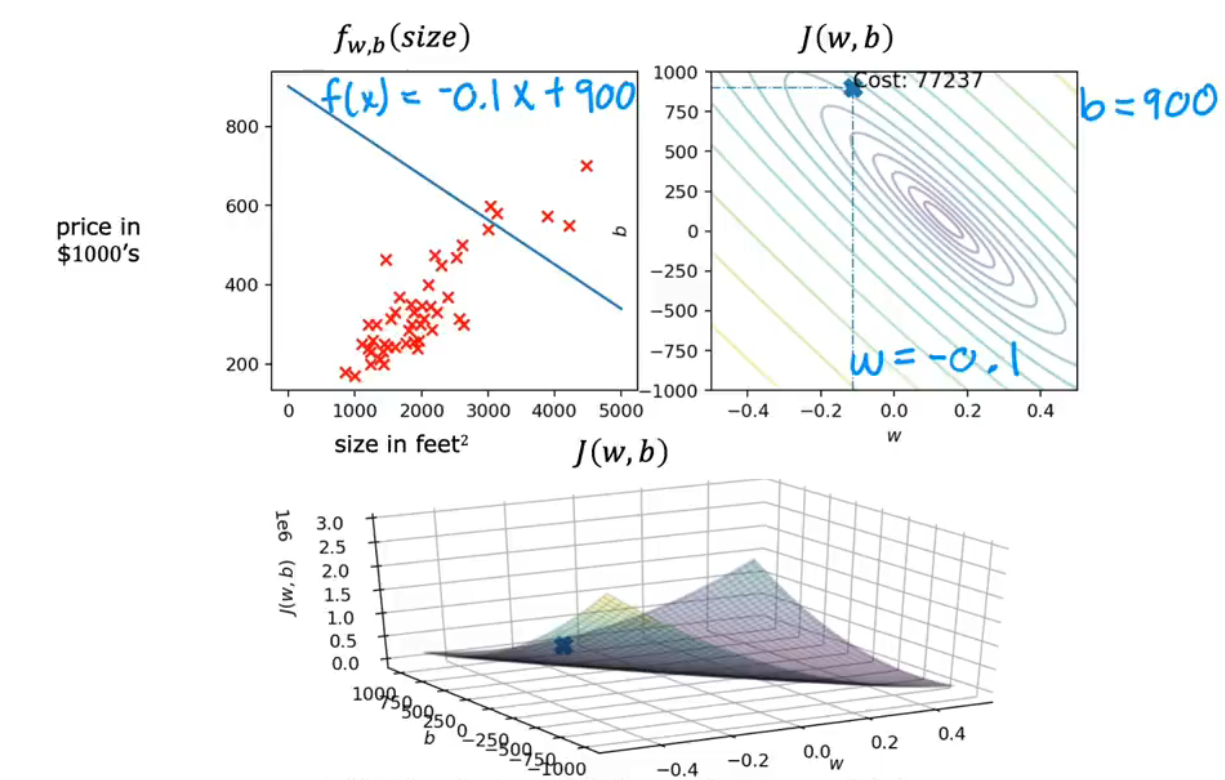
对于w,b初始化为 w = − 0.1 , b = 900 , f ( s i z e ) = − 0.1 x + 900 w=-0.1,b=900,f(size)=-0.1x+900 w=−0.1,b=900,f(size)=−0.1x+900
随着次数的增加， f ( w , b ) f(w,b) f(w,b)会越来越靠近Gloabl minimum,同时对应的直线也会更加的拟合数据
(4)Batch gradient descent / 批次梯度下降
在每一步更新中，使用的都是所有的训练集
上文所使用的就是The Batch
8.Multiple Linear Regression/多元线性回归
(1) 多维特征表示
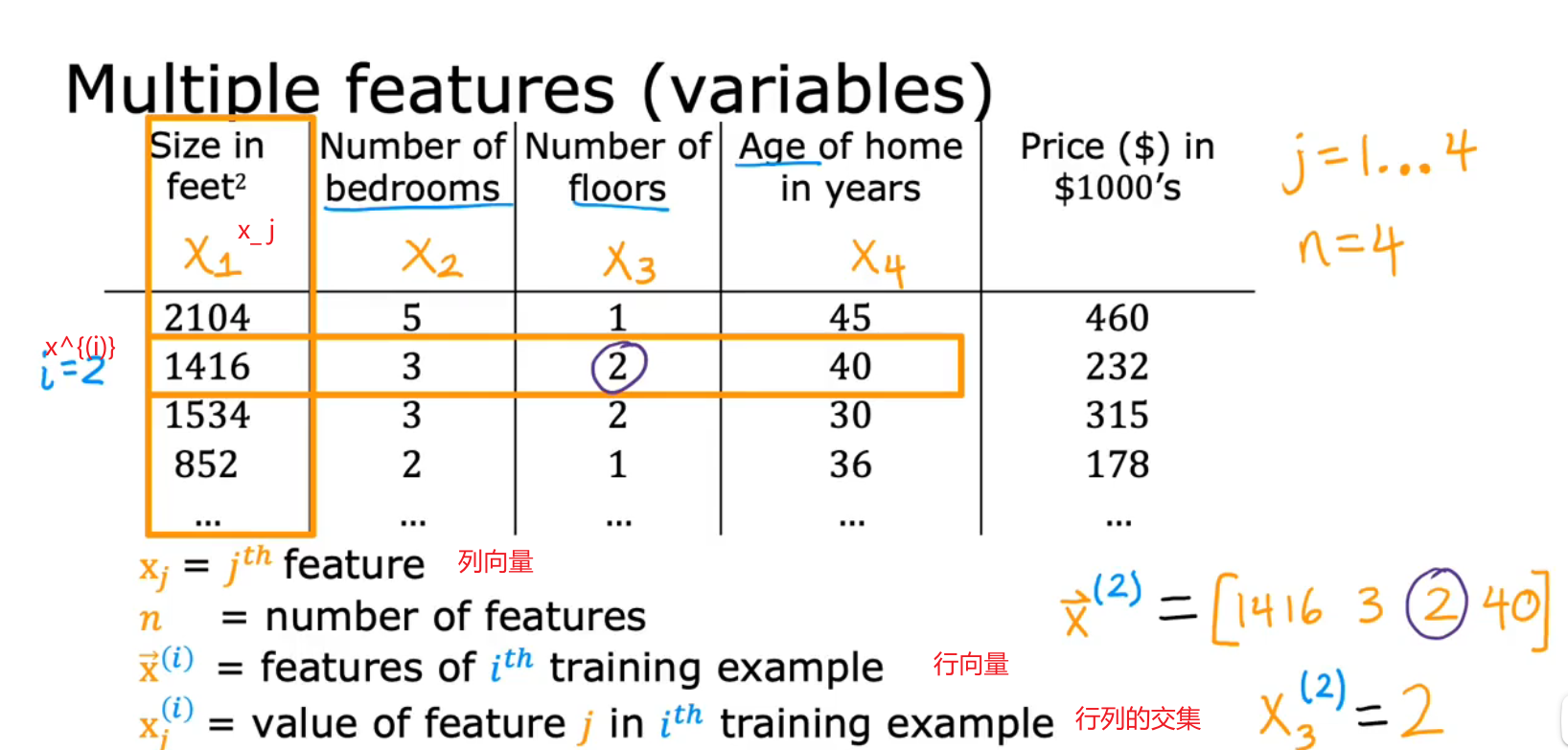
(2)函数模型
f w , b ( x ) = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b f_{w, b}(x)=w_1 x_1+w_2 x_2+\cdots+w_n x_n+b fw,b(x)=w1x1+w2x2+⋯+wnxn+b
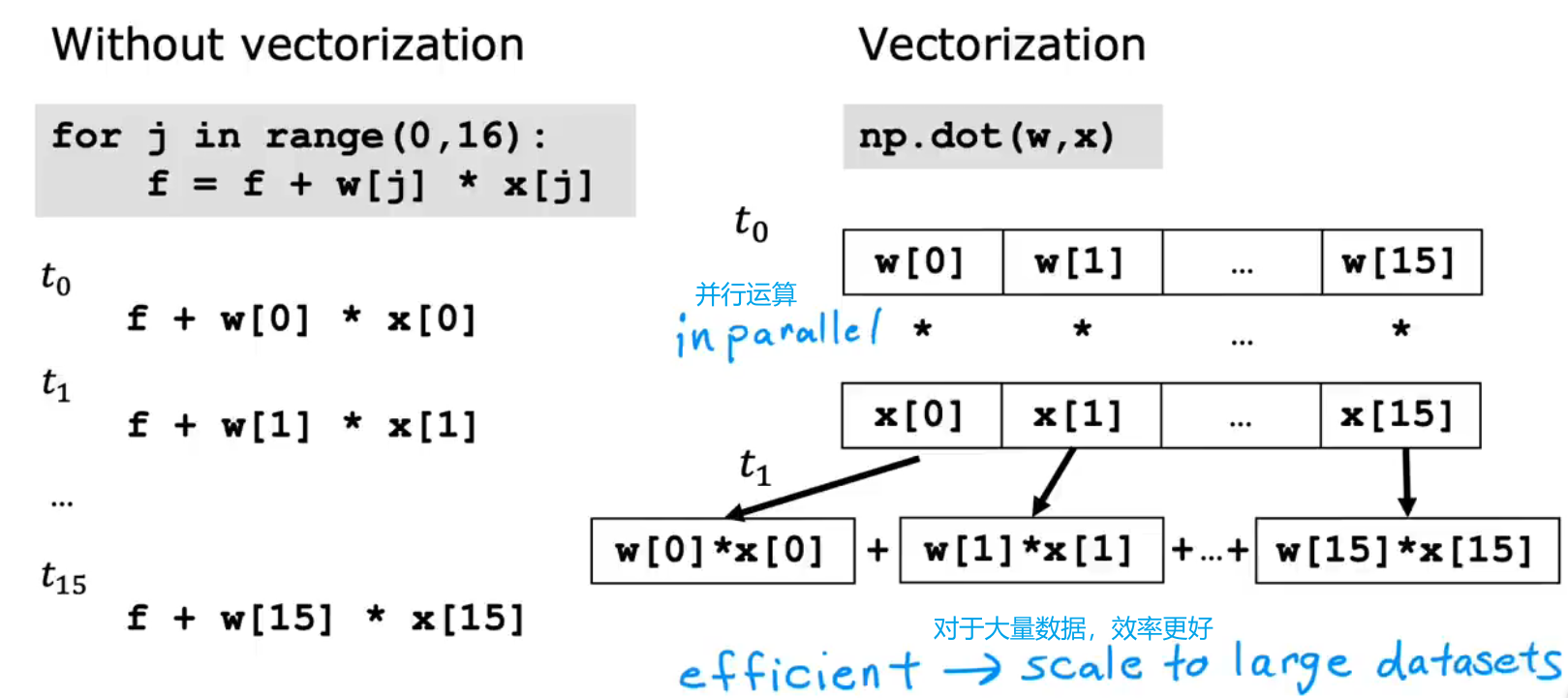
(3)vectorization/矢量化/向量化
矢量化会运用向量点乘（dot）来进行运算，当n很大时，将会大大的节省运算的时间，比循环更快
因为在计算机中Numpy的运算（+，-，dot）,以点乘（dot）为例，做的是inpanallel（并行运算），而for循环做的是串行运算
f
w
→
,
b
(
x
→
)
=
w
→
⋅
x
→
+
b
f_{\overrightarrow{\mathrm{w}}, b}(\overrightarrow{\mathrm{x}})=\overrightarrow{\mathrm{w}} \cdot \overrightarrow{\mathrm{x}}+b
fw,b(x)=w⋅x+b
#python代码实现：运用NumPy库
w=np.array([w1,w2,w3...wn])
x=np.array([x1,x2,x3...xn])
f = np.dot(w,x)+b
9.Feature Scaling / 特征缩放
可以使梯度下降运行的更快
(1)原因：
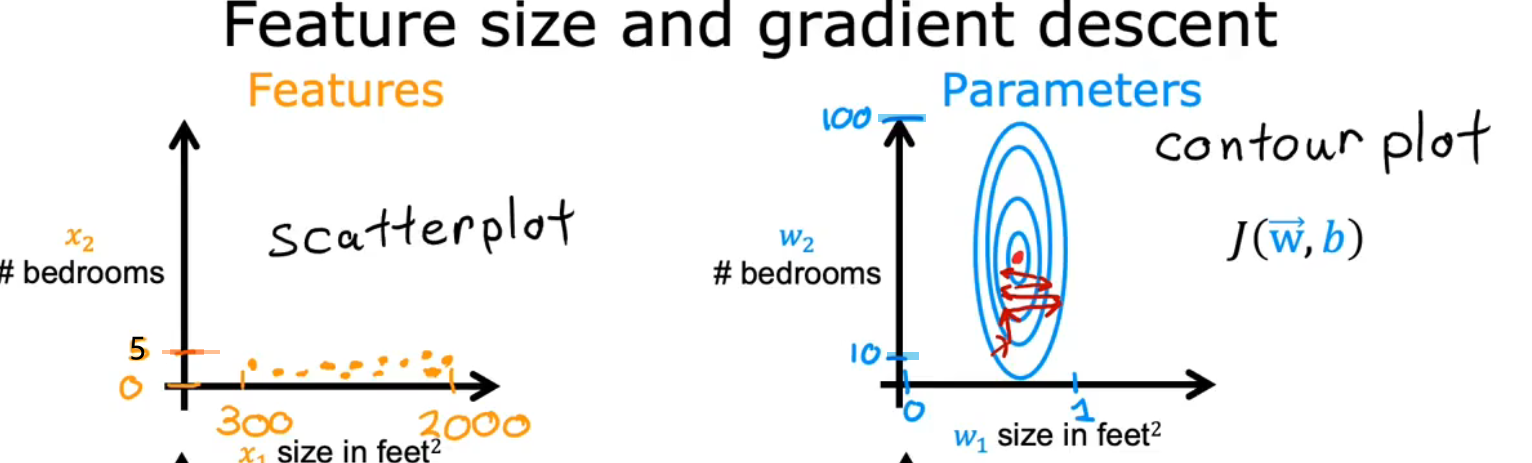
如果是数据原本的样子，那么由于不同数据之间的单位以及大小差别非常大，而导致出来的损失函数的二维图像，要么非常的瘦高，要么非常的矮胖，导致梯度下降到达global minimum的step非常多，耗费时间很大。
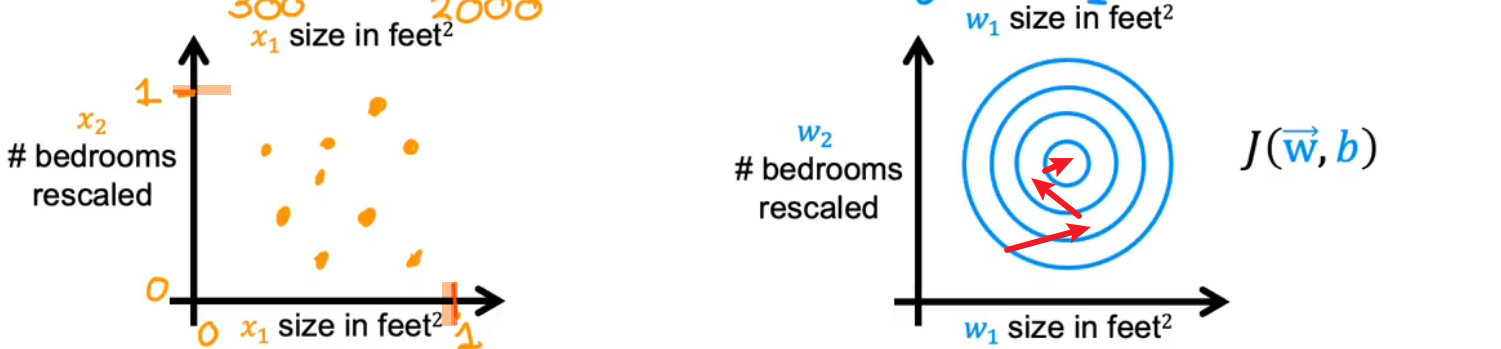
如果将数据缩放一下，使之都在0~1之间，就可以使损失函数更加的均匀，更快的到达global minimum
(2)实现
①数据除以max
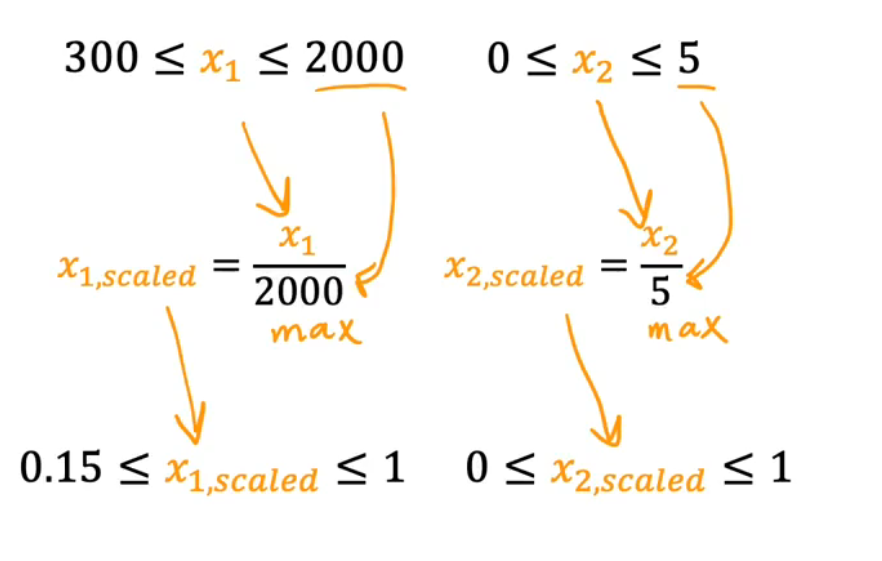
②均值归一化
让数据在(-1,1)之间
KaTeX parse error: No such environment: flalign at position 8: \begin{̲f̲l̲a̲l̲i̲g̲n̲}̲ &x_{1,scaling}…
③Z-score
x 1 = x 1 − μ 1 σ 1 x_1=\frac{x_1-\mu_1}{\sigma_1} x1=σ1x1−μ1
σ是X对应的标准差，μ是X对应的平均值
10.判断梯度下降是否收敛
(1)learning curve / 学习曲线
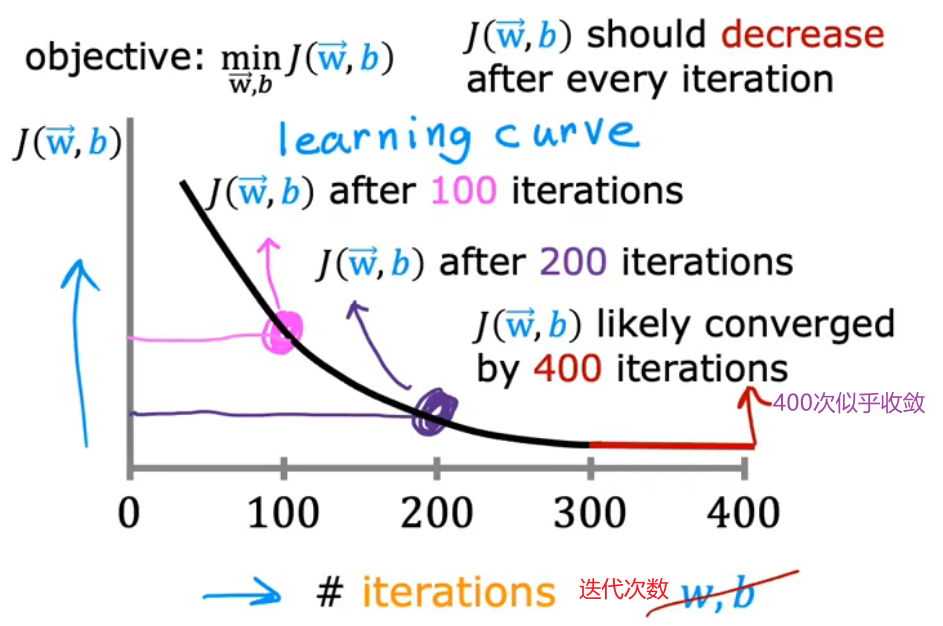
通过判断学习曲线是否收敛来判断梯度下降是否收敛
(2)Automatic convergence test / 自动收敛测试
设置一个ε"epsilon" == 0.001，如果损失函数的减小值小于ε，那么就可以判断收敛
11.如何设置学习率
(1)如果learning rate α过大的话
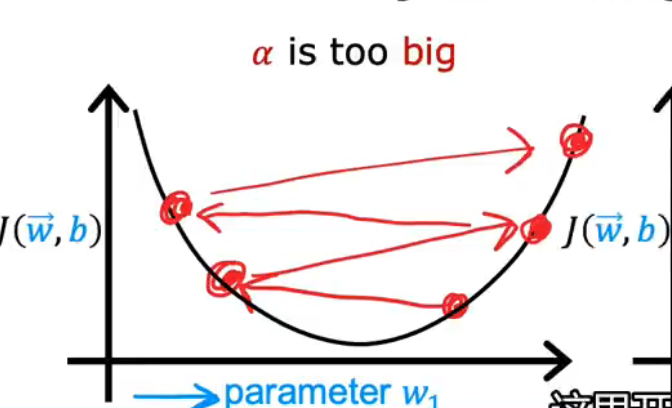
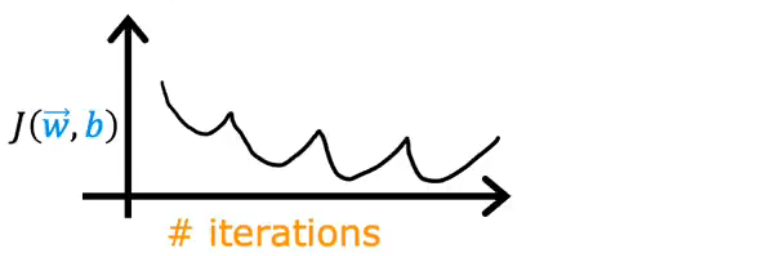
损失函数会上下变化，而不是收敛
(2)α过小的话
损失函数的变化范围极小，无法判断梯度下降是否有效
(3)DeBug
如果损失函数在增大的话，可以设置一个非常小的α，如果function仍然增大，那么就是代码出现BUG
(4)α的通常值
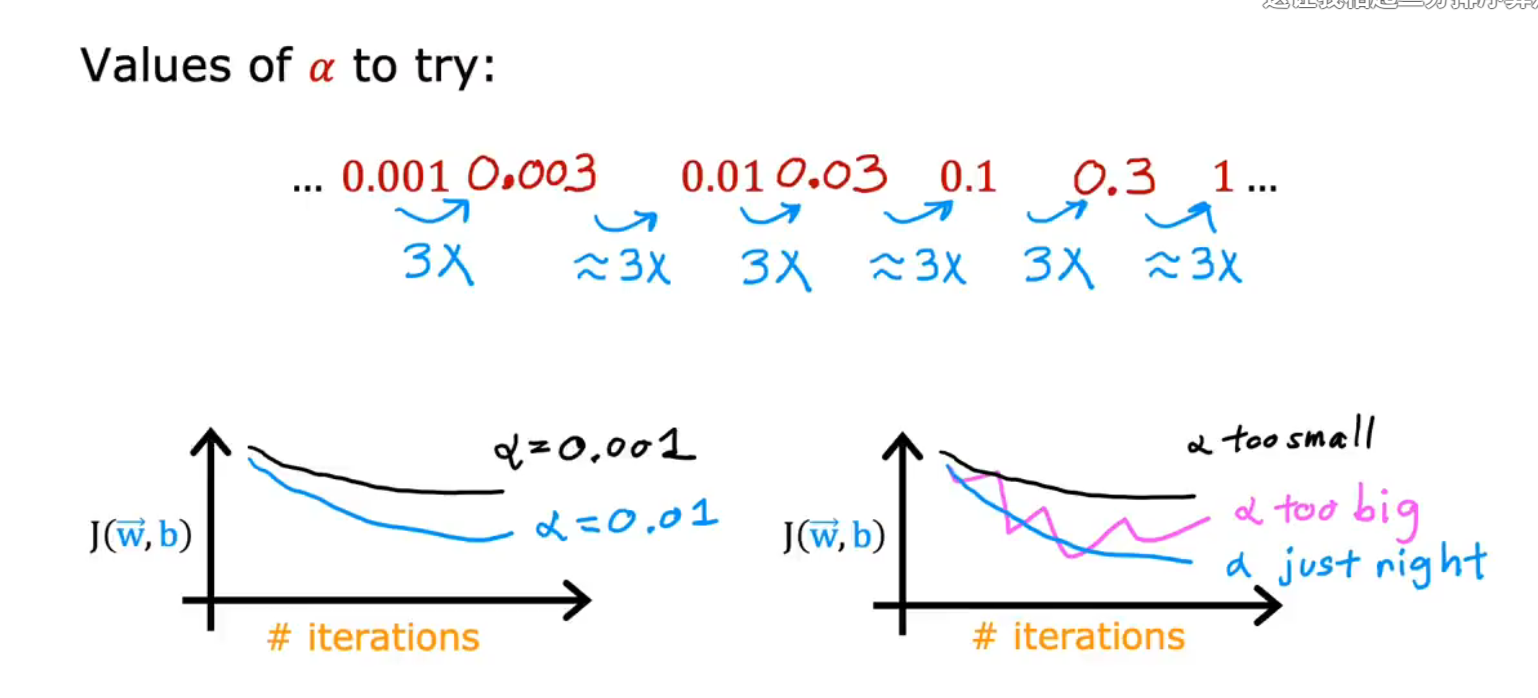
可以先从0.001开始，然后不断调参
12.Feature Engineering / 特征工程
从原来的特征中，通过transforming 或 combining来得到新的特征
13.Polynomial Regression / 多项式回归
通过选择不同的函数（一次，二次，三次，平方根等），来得到不同的曲线，找到拟合程度最好的
14.Classification / 分类
(1)Motivation / 目的
Binary Classification: only two possible outputs
(2)logistic classification / 逻辑回归
①logistic function / sigmoid function :逻辑函数
g ( z ) = 1 1 + e − z 0 < g ( z ) < 1 g(z)=\frac{1}{1+e^{-z}} \quad 0<g(z)<1 g(z)=1+e−z10<g(z)<1
②logistic regression:逻辑回归函数
z = w → ⋅ x → + b f w → , b ( x → ) = g ( w → ⋅ x → + b ⏟ z ) = 1 1 + e − ( w → ⋅ x → + b ) z=\overrightarrow{\mathrm{w}} \cdot \overrightarrow{\mathrm{x}}+b\\ f_{\overrightarrow{\mathrm{w}}, b}(\overrightarrow{\mathrm{x}})=g(\underbrace{\overrightarrow{\mathrm{w}} \cdot \overrightarrow{\mathrm{x}}+b}_{\mathrm{z}})=\frac{1}{1+e^{-(\overrightarrow{\mathrm{w}} \cdot \overrightarrow{\mathrm{x}}+b)}} z=w⋅x+bfw,b(x)=g(z w⋅x+b)=1+e−(w⋅x+b)1
注意: P ( y = 0 ) + P ( y = 1 ) = 1 P(y=0)+P(y=1)=1 P(y=0)+P(y=1)=1概率和必须为1
③决策边界 / Decision Boundary
对应的就是z==0
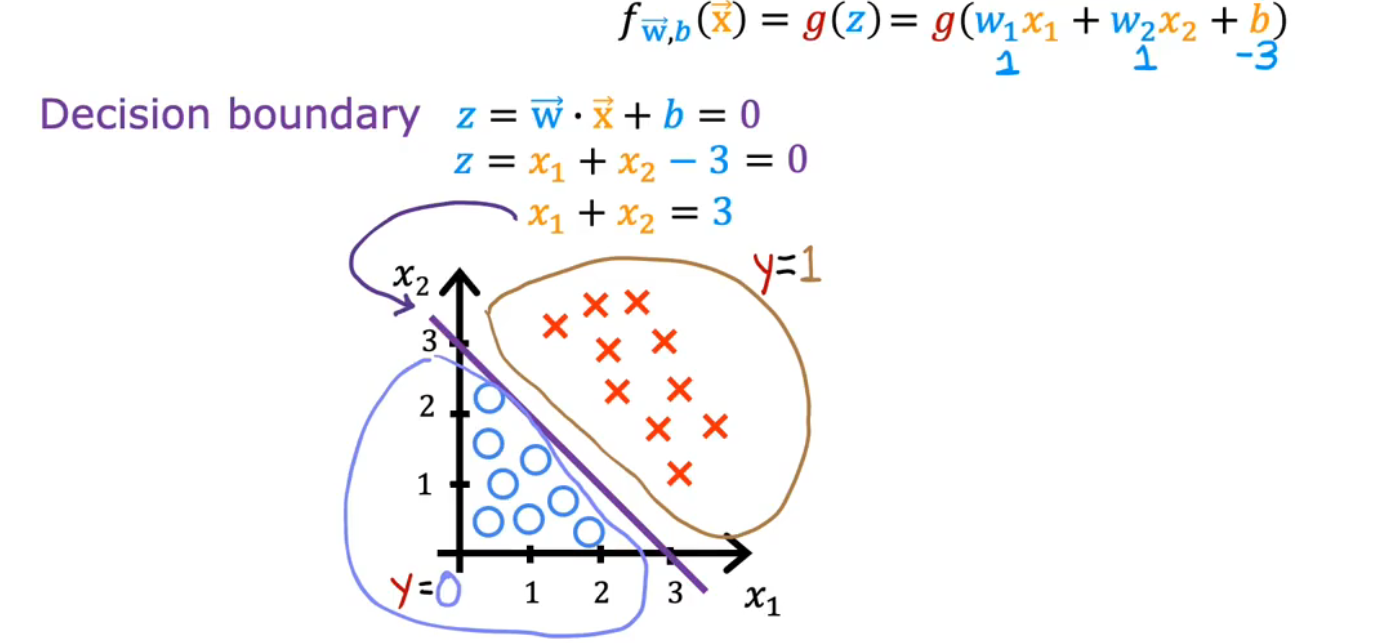
④Loss function / 损失函数
L ( f w → , b ( x → ( i ) ) , y ( i ) ) L\left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right), y^{(i)}\right) L(fw,b(x(i)),y(i))f为预测值，y为实际值
损失函数衡量的是在一个训练样例上的表现如何，通过总结获得的所有训练样例的损失
成本函数衡量的是在整个训练集上的表现
L
(
f
w
→
,
b
(
x
→
(
i
)
)
,
y
(
i
)
)
=
{
−
log
(
f
w
→
,
b
(
x
→
(
i
)
)
)
if
y
(
i
)
=
1
−
log
(
1
−
f
w
→
,
b
(
x
→
(
i
)
)
)
if
y
(
i
)
=
0
L\left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right), y^{(i)}\right)=\left\{\begin{aligned} -\log \left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)\right) & \text { if } y^{(i)}=1 \\ -\log \left(1-f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)\right) & \text { if } y^{(i)}=0 \end{aligned}\right.
L(fw,b(x(i)),y(i))=⎩
⎨
⎧−log(fw,b(x(i)))−log(1−fw,b(x(i))) if y(i)=1 if y(i)=0
y=1时：
y=0时：
⑤Cost function / 代价函数
J ( w → , b ) = 1 m ∑ i = 1 m L ( f w → , b ( x → ( i ) ) , y ( i ) ) L = { − log ( f w → , b ( x → ( i ) ) ) if y ( i ) = 1 − log ( 1 − f w → , b ( x → ( i ) ) ) if y ( i ) = 0 J(\overrightarrow{\mathrm{w}}, b)=\frac{1}{m} \sum_{i=1}^m L\left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right), y^{(i)}\right)\\ \\ L=\left\{\begin{aligned} -\log \left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)\right) & \text { if } y^{(i)}=1 \\ -\log \left(1-f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)\right) & \text { if } y^{(i)}=0 \end{aligned}\right. J(w,b)=m1i=1∑mL(fw,b(x(i)),y(i))L=⎩ ⎨ ⎧−log(fw,b(x(i)))−log(1−fw,b(x(i))) if y(i)=1 if y(i)=0
⑥简化逻辑回归代价函数
由于y只能取 0 / 1，所以可以将两个式子合并
L
(
f
w
→
,
b
(
x
→
(
i
)
)
,
y
(
i
)
)
=
−
y
(
i
)
log
(
f
w
→
,
b
(
x
→
(
i
)
)
)
−
(
1
−
y
(
i
)
)
log
(
1
−
f
w
→
,
b
(
x
→
(
i
)
)
)
J
(
w
→
,
b
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
log
(
f
w
→
,
b
(
x
→
(
i
)
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
f
w
→
,
b
(
x
→
(
i
)
)
)
]
L\left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right), y^{(i)}\right)=-y^{(i)} \log \left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)\right)-\left(1-y^{(i)}\right) \log \left(1-f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)\right) \\\\ J(\overrightarrow{\mathrm{w}}, b)=-\frac{1}{m} \sum_{i=1}^m\left[y^{(i)} \log \left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)\right)\right]
L(fw,b(x(i)),y(i))=−y(i)log(fw,b(x(i)))−(1−y(i))log(1−fw,b(x(i)))J(w,b)=−m1i=1∑m[y(i)log(fw,b(x(i)))+(1−y(i))log(1−fw,b(x(i)))]
最大似然估计
(3)实现梯度下降
w j = w j − α [ 1 m ∑ i = 1 m ( f w → , b ( x → ( i ) ) − y ( i ) ) x j ( i ) ] b = b − α [ 1 m ∑ i = 1 m ( f w → , b ( x → ( i ) ) − y ( i ) ) ] \begin{aligned} w_j & =w_j-\alpha\left[\frac{1}{m} \sum_{i=1}^m\left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)-y^{(i)}\right) x_j^{(i)}\right] \\ b & =b-\alpha\left[\frac{1}{m} \sum_{i=1}^m\left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)-y^{(i)}\right)\right] \end{aligned} wjb=wj−α[m1i=1∑m(fw,b(x(i))−y(i))xj(i)]=b−α[m1i=1∑m(fw,b(x(i))−y(i))]
15.Overfitting / 过拟合
(1)定义
过于适合训练集
high variance:高方差
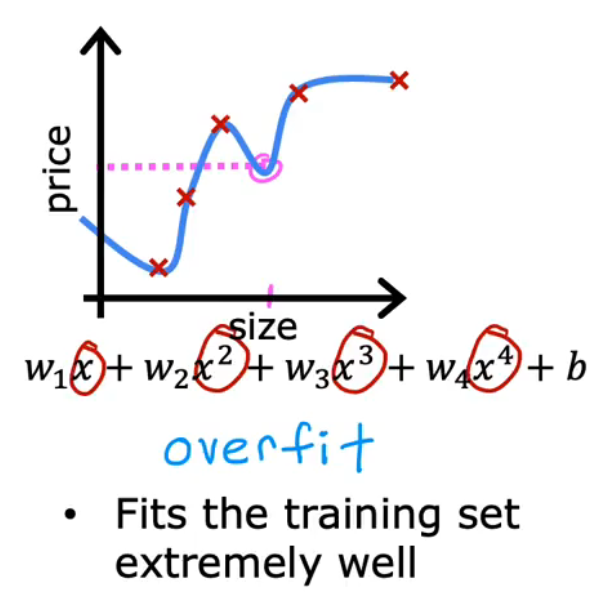
underfitting / 欠拟合：模型无法契合数据
high bais:高偏差
(2)解决过拟合:
①收集更多的数据
②用算法选择最为合适的特征数据
③正则化，来减小参数的大小
16.Regularization / 正则化
(1)作用： 保留所有的特征，但是减少参数的大小
J ( w → , b ) = 1 2 m ∑ i = 1 m ( f w → , b ( x → ( i ) ) − y ( i ) ) 2 + λ 2 m ∑ j = 1 n w j 2 λ 2 m ∑ j = 1 n w j 2 : 正则化项 λ : 正则参数 J(\overrightarrow{\mathrm{w}}, b)=\frac{1}{2 m} \sum_{i=1}^m\left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)-y^{(i)}\right)^2+\frac{\lambda}{2 m} \sum_{j=1}^n w_j^2\\ \frac{\lambda}{2 m} \sum_{j=1}^n w_j^2:正则化项\\ \lambda:正则参数 J(w,b)=2m1i=1∑m(fw,b(x(i))−y(i))2+2mλj=1∑nwj22mλj=1∑nwj2:正则化项λ:正则参数
如果λ=0，那么就不会存在正则化项，出现过拟合
如果λ无限大，那么W，就会非常小，导致 f ( x ) = b f(x)=b f(x)=b，出现欠拟合
(2)梯度下降
w
j
=
w
j
−
α
[
1
m
∑
i
=
1
m
[
(
f
w
→
,
b
(
x
→
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
]
+
λ
m
w
j
]
b
=
b
−
α
1
m
∑
i
=
1
m
(
f
w
→
,
b
(
x
→
(
i
)
)
−
y
(
i
)
)
\begin{aligned} w_j & =w_j-\alpha\left[\frac{1}{m} \sum_{i=1}^m\left[\left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)-y^{(i)}\right) x_j^{(i)}\right]+\frac{\lambda}{m} w_j\right] \\ b & =b-\alpha \frac{1}{m} \sum_{i=1}^m\left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)-y^{(i)}\right) \end{aligned}
wjb=wj−α[m1i=1∑m[(fw,b(x(i))−y(i))xj(i)]+mλwj]=b−αm1i=1∑m(fw,b(x(i))−y(i))
w,b进行同步跟新
修改后的逻辑分类成本函数：
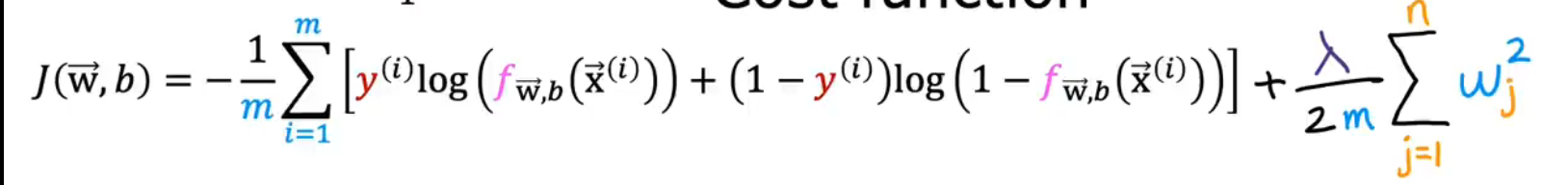
J
(
w
→
,
b
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
log
(
f
w
→
,
b
(
x
→
(
i
)
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
f
w
→
,
b
(
x
→
(
i
)
)
)
]
+
λ
2
m
∑
j
=
1
n
w
j
2
J(\overrightarrow{\mathrm{w}}, b)=-\frac{1}{m} \sum_{i=1}^m\left[y^{(i)} \log \left(f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-f_{\overrightarrow{\mathrm{w}}, b}\left(\overrightarrow{\mathrm{x}}^{(i)}\right)\right)\right]+\frac{\lambda}{2 m} \sum_{j=1}^n w_j^2
J(w,b)=−m1i=1∑m[y(i)log(fw,b(x(i)))+(1−y(i))log(1−fw,b(x(i)))]+2mλj=1∑nwj2
17.Neural Network / 神经网络
Neuron 神经元：装有一个数字 number的容器（数字代表一些特征，例如图像的灰度值）
Activation 激活值：神经元里的number(激活值越大，代表神经元越亮)，大小处在（0，1）
权重：下一层的神经元与上一层的神经元之间存在的数
用Sigma函数，将加权和映射在Activation中
只有当加权和大于10时，激发才有意义，所以加上一个-10的偏执（保证不会过早激发）
每一个神经元都与上一层所有的神经元相连接，也就是存在784个weight，而每一层有16个神经元，所以一层有784*16个权重和16个偏执
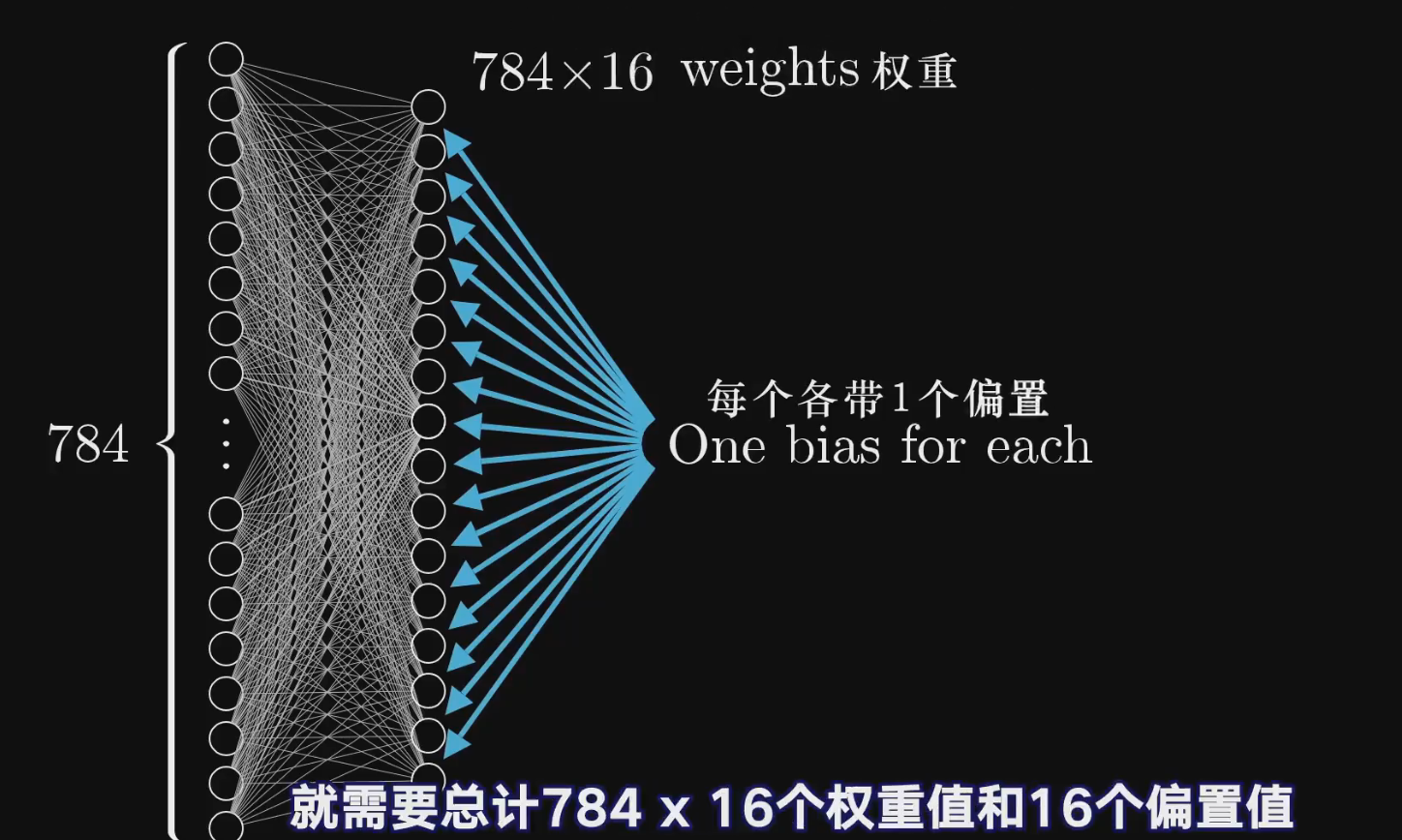
四层神经网络共有 784 ∗ 16 + 16 ∗ 16 + 16 ∗ 10 784*16+16*16+16*10 784∗16+16∗16+16∗10个weight，以及 16 + 16 + 10 16+16+10 16+16+10个bias，总共13002个参数
矩阵：
这一列的神经元代表这上一层的神经元
这一列的偏执，代表这一层上每一个的神经元的偏执
每一行的W乘以一列a，再加上一个b，就代表了这一层的一个神经元
18.Backpropagation / 反向传播
通过训练样本最终改变wieght 和 bias（负反馈）
(1)增加一个神经元的激活值
- 增加b
- 增加w：就是增加 a j a_j aj神经元的比重
- 改变 a j a_j aj：改变前一层的激活值
①增加bias
②增加w
依据 a j a_j aj神经元来改变weight
选择一个性价比最高的参数：比起增大连接黯淡神经元的权重，增大明亮神经元的权重所造成的影响更大
③改变 a j a_j aj
改变前一层的激活值
如果所有正权重的神经元更加亮，而所有负权重连接的神经元更加暗淡，那么这个神经元就会更加强烈的激发
选择更有性价比的神经元：依据对应权重的大小，对激活值做出呈比例的改变
(2)改变前一层
最后从全局来看，还需要最后一层其余的神经元的激发变弱
最后把所有神经元的变化加起来，来作为对倒数第二层神经元的激活值改变的指示
然后一直循环到第一层
(3)推广
注意要对所有的训练集进行一遍
(4)优化：随机梯度下降
选取一定量的数据作为minibatch，对minibatch进行训练，得到一个近似梯度，调整参数，不断循环
19.卷积神经网络 / CNNS
Convolutional Neural Network
参考博客：
CS231n课程笔记翻译：卷积神经网络笔记 - 知乎 (zhihu.com)
(1)概念
①由神经元组成
神经元中有具有学习能力的权重和偏差。每个神经元都得到一些输入数据，进行内积运算后再进行激活函数运算。
②卷积神经网络的结构基于一个假设：即输入数据是图像。
整个网络依旧是一个可导的评分函数：该函数的输入是原始的图像像素，输出是不同类别的评分。在最后一层（往往是全连接层），网络依旧有一个损失函数（比如SVM或Softmax），并且在神经网络中我们实现的各种技巧和要点依旧适用于卷积神经网络。
③神经元的三维排列。
卷积神经网络的各层中的神经元是3维排列的：宽度、高度和深度（这里的深度指的是激活数据体的第三个维度，而不是整个网络的深度，整个网络的深度指的是网络的层数）
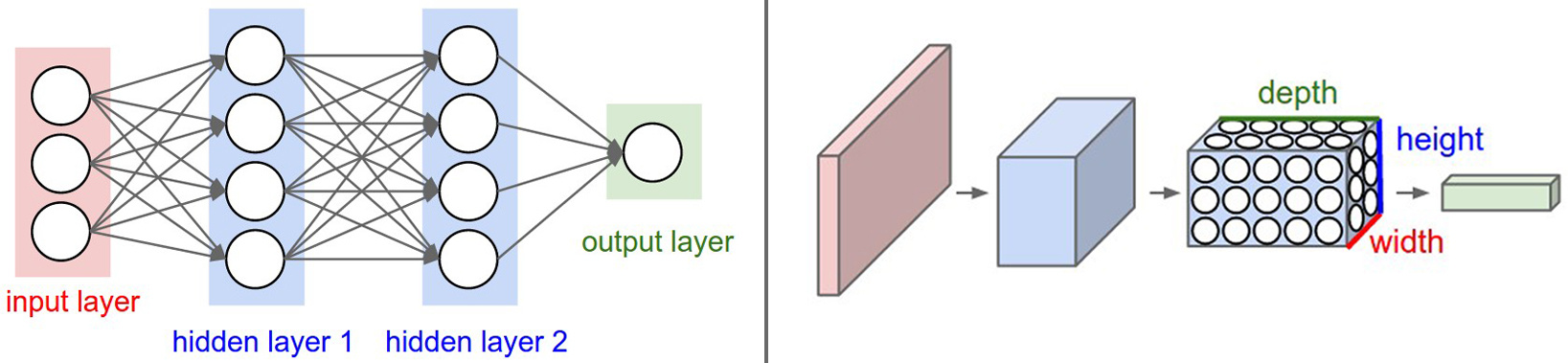
左边是一个3层的神经网络。右边是一个卷积神经网络，图例中网络将它的神经元都排列成3个维度（宽、高和深度）。卷积神经网络的每一层都将3D的输入数据变化为神经元3D的激活数据并输出。在这个例子中，红色的输入层装的是图像，所以它的宽度和高度就是图像的宽度和高度，它的深度是3（代表了红、绿、蓝3种颜色通道）。
卷积神经网络是由层组成的。每一层都有一个简单的API：用一些含或者不含参数的可导的函数，将输入的3D数据变换为3D的输出数据。
(2)层级结构
一个简单的卷积神经网络是由各种层按照顺序排列组成，网络中的每个层使用一个可以微分的函数将激活数据从一个层传递到另一个层。卷积神经网络主要由三种类型的层构成：卷积层，汇聚（Pooling）层和全连接层（全连接层和常规神经网络中的一样）。通过将这些层叠加起来，就可以构建一个完整的卷积神经网络。
①数据输入层
该层要做的处理主要是对原始图像数据进行预处理，其中包括：
- 去均值：把输入数据各个维度都中心化为0，如下图所示，其目的就是把样本的中心拉回到坐标系原点上。
- 归一化：幅度归一化到同样的范围，如下所示，即减少各维度数据取值范围的差异而带来的干扰，比如，我们有两个维度的特征A和B，A范围是0到10，而B范围是0到10000，如果直接使用这两个特征是有问题的，好的做法就是归一化，即A和B的数据都变为0到1的范围。
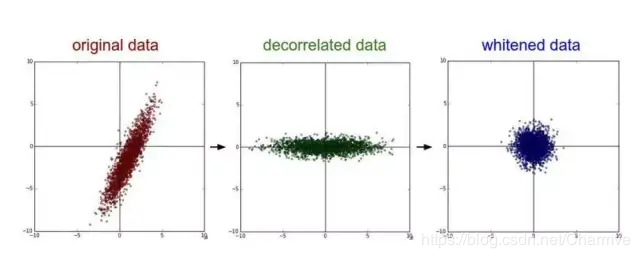
- PCA/白化：用PCA降维；白化是对数据各个特征轴上的幅度归一化
去均值与归一化效果图：
去相关与白化效果图：
②卷积层
卷积层是构建卷积神经网络的核心层，它产生了网络中大部分的计算量。
②.1两个关键操作
-
局部关联。每个神经元看做一个滤波器(filter)
也就是卷积核
-
窗口(receptive field)滑动， filter对局部数据计算
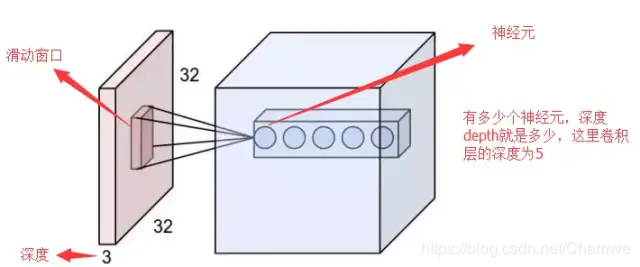
②.2名词
-
深度/depth（解释见下图）
-
步幅/stride （窗口一次滑动的长度）
-
填充值/zero-padding
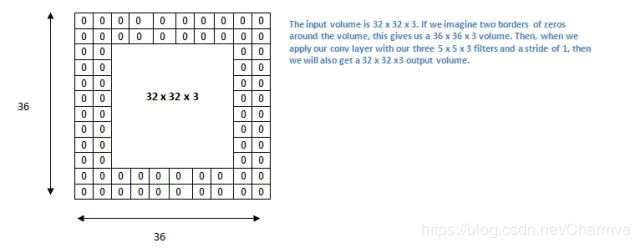
②.3填充值
把 5 x 5 x 3 的过滤器用在 32 x 32 x 3 的输入上时，会发生什么？输出的大小会是 28 x 28 x 3。注意，这里空间维度减小了。如果我们继续用卷积层，尺寸减小的速度就会超过我们的期望。在网络的早期层中，我们想要尽可能多地保留原始输入内容的信息，这样我们就能提取出那些低层的特征。比如说我们想要应用同样的卷积层，但又想让输出量维持为 32 x 32 x 3 。为做到这点，我们可以对这个层应用大小为 2 的零填充（zero padding）。零填充在输入内容的边界周围补充零。如果我们用两个零填充，就会得到一个 36 x 36 x 3 的输入卷。
注意：
如果stride==1时，把zero padding 设置为
Zero Padding
=
(
K
−
1
)
2
K
是卷积核的尺寸
\text { Zero Padding }=\frac{(K-1)}{2} \\K是卷积核的尺寸
Zero Padding =2(K−1)K是卷积核的尺寸
此时输入与输出的内容就会保持一致的空间维度
计算任意给定卷积层的输出的大小的公式是
O
=
(
W
−
K
+
2
P
)
S
+
1
O
是输出尺寸，
K
是卷积核尺寸，
P
是填充，
S
是步幅。
O=\frac{(W-K+2 P)}{S}+1 \\O 是输出尺寸，K 是卷积核尺寸，P 是填充，S 是步幅。
O=S(W−K+2P)+1O是输出尺寸，K是卷积核尺寸，P是填充，S是步幅。
②.4概述
卷积层的参数是有一些可学习的滤波器集合构成的。每个滤波器在空间上（宽度和高度）都比较小，但是深度和输入数据一致。举例来说，卷积神经网络第一层的一个典型的滤波器的尺寸可以是5x5x3（宽高都是5像素，深度是3是因为图像应为颜色通道，所以有3的深度）。在前向传播的时候，让每个滤波器都在输入数据的宽度和高度上滑动（更精确地说是卷积），然后计算整个滤波器和输入数据任一处的内积。当滤波器沿着输入数据的宽度和高度滑过后，会生成一个2维的激活图（activation map），激活图给出了在每个空间位置处滤波器的反应。直观地来说，网络会让滤波器学习到当它看到某些类型的视觉特征时就激活，具体的视觉特征可能是某些方位上的边界，或者在第一层上某些颜色的斑点，甚至可以是网络更高层上的蜂巢状或者车轮状图案。
在每个卷积层上，我们会有一整个集合的滤波器（比如12个），每个都会生成一个不同的二维激活图。将这些激活映射在深度方向上层叠起来就生成了输出数据。
②.5局部连接
在处理图像这样的高维度输入时，让每个神经元都与前一层中的所有神经元进行全连接是不现实的。相反，我们让每个神经元只与输入数据的一个局部区域连接。该连接的空间大小叫做神经元的感受野（receptive field），它的尺寸是一个超参数（其实就是滤波器的空间尺寸）。在深度方向上，这个连接的大小总是和输入量的深度相等。需要再次强调的是，我们对待空间维度（宽和高）与深度维度是不同的：连接在空间（宽高）上是局部的，但是在深度上总是和输入数据的深度一致。
②.6卷积运算
下面蓝色矩阵周围有一圈灰色的框，那些就是上面所说到的填充值，蓝色矩阵就是输入的图像，粉色矩阵就是卷积层的神经元，这里表示了有两个神经元（w0,w1）。绿色矩阵就是经过卷积运算后的输出矩阵，这里的步长设置为2。
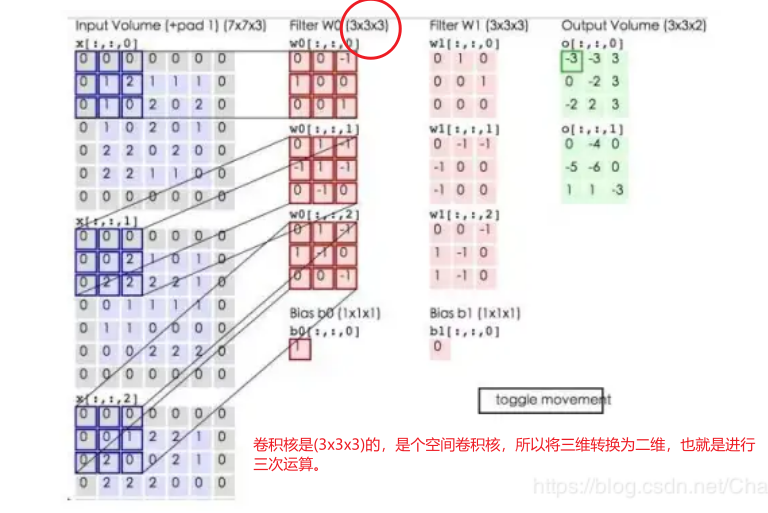
蓝色的矩阵(输入图像)对粉色的矩阵（filter）进行矩阵内积计算并将三个内积运算的结果与偏置值b相加（比如上面图的计算：2+（-2+1-2）+（1-2-2） + 1= 2 - 3 - 3 + 1 = -3），计算后的值就是绿框矩阵的一个元素。
动态图形象地展示了卷积层的计算过程：
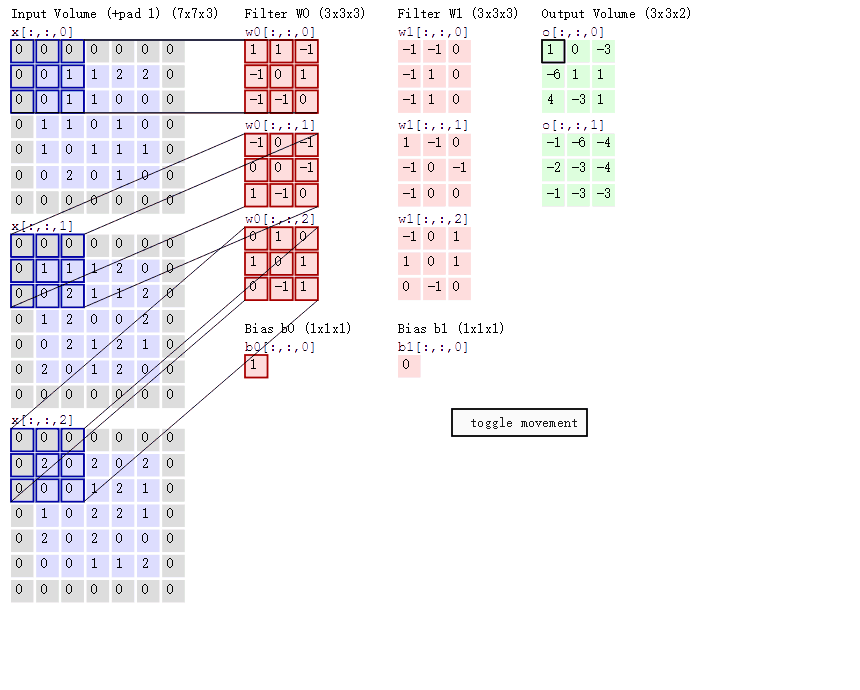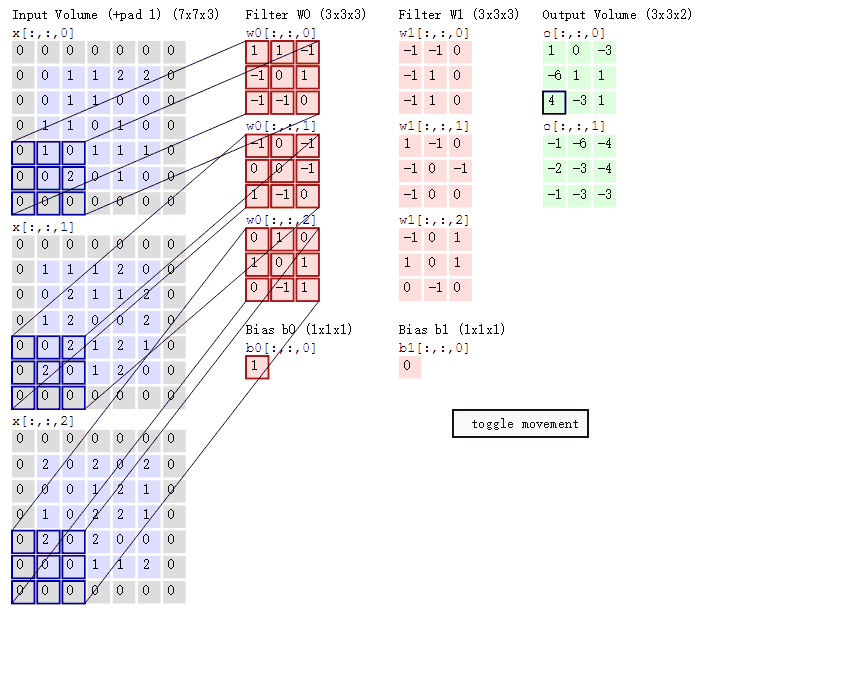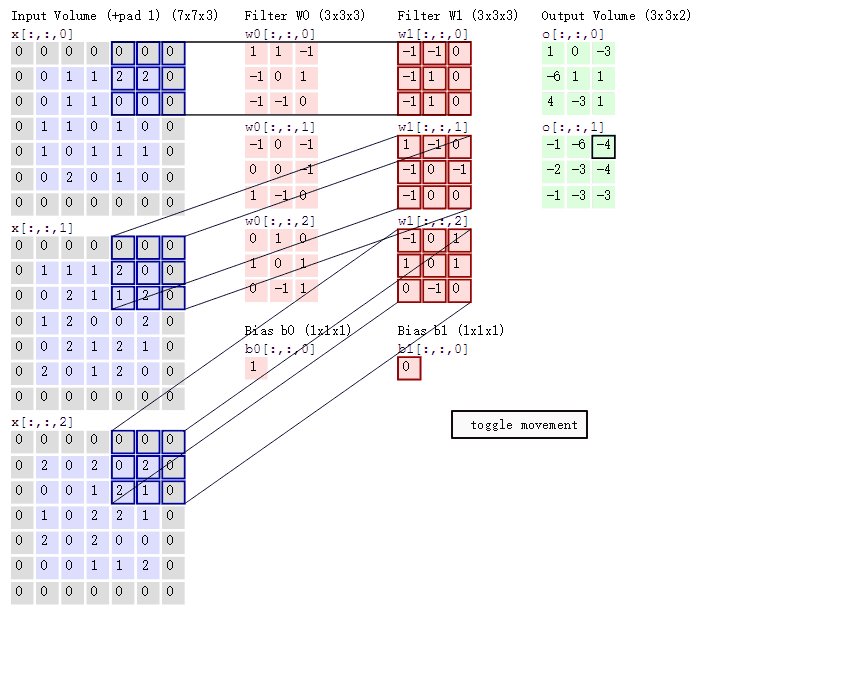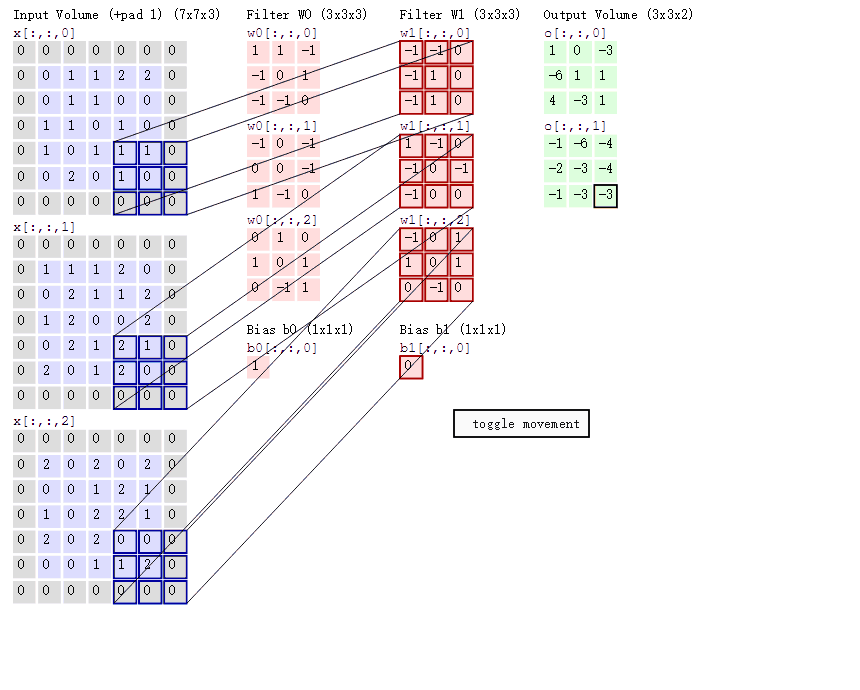
②.7参数共享机制
②.8非线性层/ 激活层
把卷积层输出结果做非线性映射。
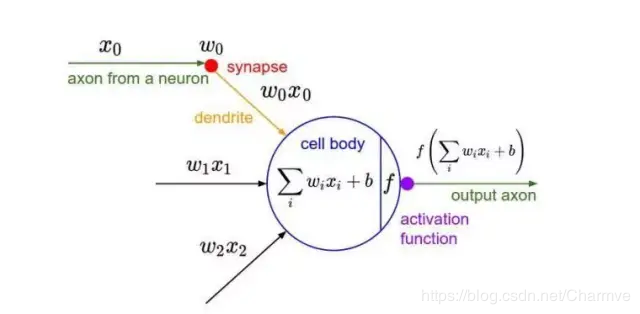
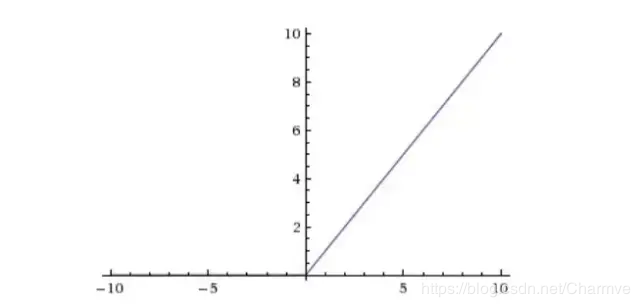
CNN采用的激活函数一般为ReLU(The Rectified Linear Unit/修正线性单元)，它的特点是收敛快，求梯度简单，但较脆弱，图像如下。
激励层的实践经验：
- 不要用sigmoid！不要用sigmoid！不要用sigmoid！
- 首先试RELU，因为快，但要小心点
- 如果2失效，请用Leaky ReLU或者Maxout
- 某些情况下tanh倒是有不错的结果，但是很少
②.9池化层
池化层夹在连续的卷积层中间， 用于压缩数据和参数的量，减小过拟合。
简而言之，如果输入是图像的话，那么池化层的最主要作用就是压缩图像。
作用：
- 特征不变性，也就是我们在图像处理中经常提到的特征的尺度不变性，池化操作就是图像的resize，平时一张狗的图像被缩小了一倍我们还能认出这是一张狗的照片，这说明这张图像中仍保留着狗最重要的特征，我们一看就能判断图像中画的是一只狗，图像压缩时去掉的信息只是一些无关紧要的信息，而留下的信息则是具有尺度不变性的特征，是最能表达图像的特征。
- 特征降维，我们知道一幅图像含有的信息是很大的，特征也很多，但是有些信息对于我们做图像任务时没有太多用途或者有重复，我们可以把这类冗余信息去除，把最重要的特征抽取出来，这也是池化操作的一大作用。
- 在一定程度上防止过拟合，更方便优化。
常用方法：Max Pooling 和 Average Pooling，最常用的Max Pooling
对于每个窗口选出最大的数作为输出矩阵的相应元素的值
②.10全连接层
两层之间所有神经元都有权重连接，通常全连接层在卷积神经网络尾部。也就是跟传统的神经网络神经元的连接方式是一样的
一般CNN结构依次为
- INPUT
2. [[CONV -> RELU]N -> POOL?]M
3. [FC -> RELU]*K
4. FC
(3)训练算法
- 同一般机器学习算法，先定义Loss function，衡量和实际结果之间差距。
- 找到最小化损失函数的W和b， CNN中用的算法是SGD（随机梯度下降）。
(4)优缺点
优点：
- 共享卷积核，对高维数据处理无压力
- 无需手动选取特征，训练好权重，即得特征分类效果好
缺点：
- 需要调参，需要大样本量，训练最好要GPU
- 物理含义不明确（也就说，我们并不知道没个卷积层到底提取到的是什么特征，而且神经网络本身就是一种难以解释的“黑箱模型”）
(5)fine-tuning
Fine-tuning是指在一个已经训练好的模型基础上，进一步在特定任务上进行训练，从而使模型适应该任务的特定数据和要求。
通常情况下，我们会使用一个在大规模数据上预训练的模型作为基础模型，然后在特定的任务上进行fine-tuning，以获得更好的性能。
Fine-tuning的优点在于，它可以充分利用预训练模型在大规模数据上学到的特征和知识，从而在小数据集上也能获得较好的性能。此外，Fine-tuning还可以节省大量的训练时间和计算资源，因为我们可以直接在预训练模型的基础上进行训练，而不需要从头开始训练一个新的模型。
(5)总结
①卷积网络在本质上是一种输入到输出的映射，它能够学习大量的输入与输出之间的映射关系，而不需要任何输入和输出之间的精确的数学表达式，只要用已知的模式对卷积网络加以训练，网络就具有输入输出对之间的映射能力。
②CNN一个非常重要的特点就是头重脚轻（越往输入权值越小，越往输出权值越多），呈现出一个倒三角的形态，这就很好地避免了BP神经网络中反向传播的时候梯度损失得太快。
③卷积神经网络CNN主要用来识别位移、缩放及其他形式扭曲不变性的二维图形。由于CNN的特征检测层通过训练数据进行学习，所以在使用CNN时，避免了显式的特征抽取，而隐式地从训练数据中进行学习；再者由于同一特征映射面上的神经元权值相同，所以网络可以并行学习，这也是卷积网络相对于神经元彼此相连网络的一大优势。权值共享降低了网络的复杂性，特别是多维输入向量的图像可以直接输入网络这一特点避免了特征提取和分类过程中数据重建的复杂度。
积核，对高维数据处理无压力
2. 无需手动选取特征，训练好权重，即得特征分类效果好
缺点：
- 需要调参，需要大样本量，训练最好要GPU
- 物理含义不明确（也就说，我们并不知道没个卷积层到底提取到的是什么特征，而且神经网络本身就是一种难以解释的“黑箱模型”）
(5)fine-tuning
Fine-tuning是指在一个已经训练好的模型基础上，进一步在特定任务上进行训练，从而使模型适应该任务的特定数据和要求。
通常情况下，我们会使用一个在大规模数据上预训练的模型作为基础模型，然后在特定的任务上进行fine-tuning，以获得更好的性能。
Fine-tuning的优点在于，它可以充分利用预训练模型在大规模数据上学到的特征和知识，从而在小数据集上也能获得较好的性能。此外，Fine-tuning还可以节省大量的训练时间和计算资源，因为我们可以直接在预训练模型的基础上进行训练，而不需要从头开始训练一个新的模型。
(5)总结
①卷积网络在本质上是一种输入到输出的映射，它能够学习大量的输入与输出之间的映射关系，而不需要任何输入和输出之间的精确的数学表达式，只要用已知的模式对卷积网络加以训练，网络就具有输入输出对之间的映射能力。
②CNN一个非常重要的特点就是头重脚轻（越往输入权值越小，越往输出权值越多），呈现出一个倒三角的形态，这就很好地避免了BP神经网络中反向传播的时候梯度损失得太快。
③卷积神经网络CNN主要用来识别位移、缩放及其他形式扭曲不变性的二维图形。由于CNN的特征检测层通过训练数据进行学习，所以在使用CNN时，避免了显式的特征抽取，而隐式地从训练数据中进行学习；再者由于同一特征映射面上的神经元权值相同，所以网络可以并行学习，这也是卷积网络相对于神经元彼此相连网络的一大优势。权值共享降低了网络的复杂性，特别是多维输入向量的图像可以直接输入网络这一特点避免了特征提取和分类过程中数据重建的复杂度。
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
