CF449D Jzzhu and Numbers 题解

CF449D Jzzhu and Numbers

题意

给定 $A_1....A_n$，选任意个数使得它们与和为 $0$，求方案数。

思路

很朴素的想法是枚举每个数，然后进行 0-1 背包方案数统计，时间复杂度 $O(n\times n)$。

而根据前面几题的经验，这种与运算等于 $0$ 且统计数量的题，应该和 SoS dp 有关。

$f(x)$ 的设计

如果采用一般 SoS dp 的定义， $f(x)$ 表示的是多少个数是 $x$ 的子集，$g(x)$ 表示选择的数的与和是 $x$ 的子集的方案数。

两者并无直接联系，需要做些调整，考虑重新设计状态。

容斥原理统计方案数

记 $f(x)$ 为 $x$ 是多少个数的子集。

那么若 $x$ 二进制下的第 $i$ 位为 $1$，$f(x)$ 对应集合中的任意一个数，应满足数第 $i$ 位为 $1$。

记 $g(x)$ 为 $x$ 是选择的数的与和的子集的方案数。

那么若 $x$ 二进制下的第 $i$ 位为 $1$，$g(x)$ 对应集合中的任意一组选择方案，应满足选择的数的第 $i$ 全部均为 $1$。

所以 $g(x)$ 对应集合中的元素均属于 $f(x)$ 对应集合，得 $g(x)=2^{f(x)}-1$（减掉空集的情况）。

以 A = { 0 , 1 , 2 , 3 } A=\lbrace {0,1,2,3} \rbrace A={0,1,2,3} 为例，下图中代表的是 $g(x)$ 所对应的集合：

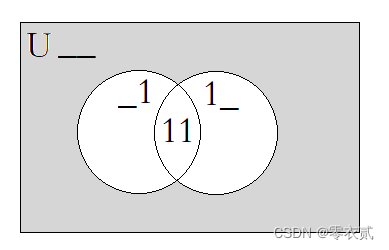
答案即为灰色部分。

考虑采用容斥原理求解并集：若二进制中 $1$ 的个数为奇数，则符号为正，反之为负。

对于 $f(x)$ 的求解

1. 改转移方程

一般的 SoS dp 中，统计 $mask$ 的子集，有：

$S(mask,i)=\{\begin{array}{ll}S(mask,i-1)& i^{th}bitoff\\ S(mask,i-1)\cup S(mask\oplus 2^i,i-1)& i^{th}biton\end{array}$

现统计 $mask$ 是哪些数的子集，有：

$S(mask,i)=\{\begin{array}{ll}S(mask,i-1)& i^{th}biton\\ S(mask,i-1)\cup S(mask\oplus 2^i,i-1)& i^{th}bitoff\end{array}$

code version 1

2. 取反后统计

记 $a$ 取反为 $a^{\prime }$，$b$ 取反为 $b^{\prime }$。

若 $a\subseteq b$，那么 $b^{\prime }\subseteq a^{\prime }$。

若有 $k$ 个数是 $mas{k}^{\prime }$ 的子集，那么 $f(mask)=k$。

code version 2