验证四个事件概率的加法公式 用卡诺图形式的表格加加减减

四个事件概率的加法公式

P(A+B+C+D)=P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)-P(AD)-P(BC)-P(BD)-P(CD)+P(ABC)+P(ABD)+P(ACD)+P(BCD)-P(ABCD)

用数字表示每一部分的重叠块数

用类似卡诺图的形式表示四个事件的重叠面积块数

从重叠块数最多的写起,可以保证重叠面积块数少的有唯一确定的位置

以上是P(A)+P(B)+P(C)+P(D)的结果,图中数字的位置代表的是包含事件最多的重叠面积的块数,比如中间的4代表同时包含ABCD的面积的块数,但它也同时属于A,B,C和D,对于最下面的3,它处于的最精确的位置是ACD,准确的说是AB'CD,不过不管它,此时中间的4的位置也可以是ACD,但从重叠次数多的面积开始写可以避免这个问题,所以最下面的3就代表ACD包含面积重叠的块数,而不是AC或者CD.

P(A)+P(B)+P(C)+P(D)的重叠部分非常多,按照公式

P(A+B+C+D)=P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)-P(AD)-P(BC)-P(BD)-P(CD)+P(ABC)+P(ABD)+P(ACD)+P(BCD)-P(ABCD)

依次减去重叠部分的块数

P(A)+P(B)+P(C)+P(D)-P(AB)

P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)

P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)-P(AD)

P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)-P(AD)-P(BC)

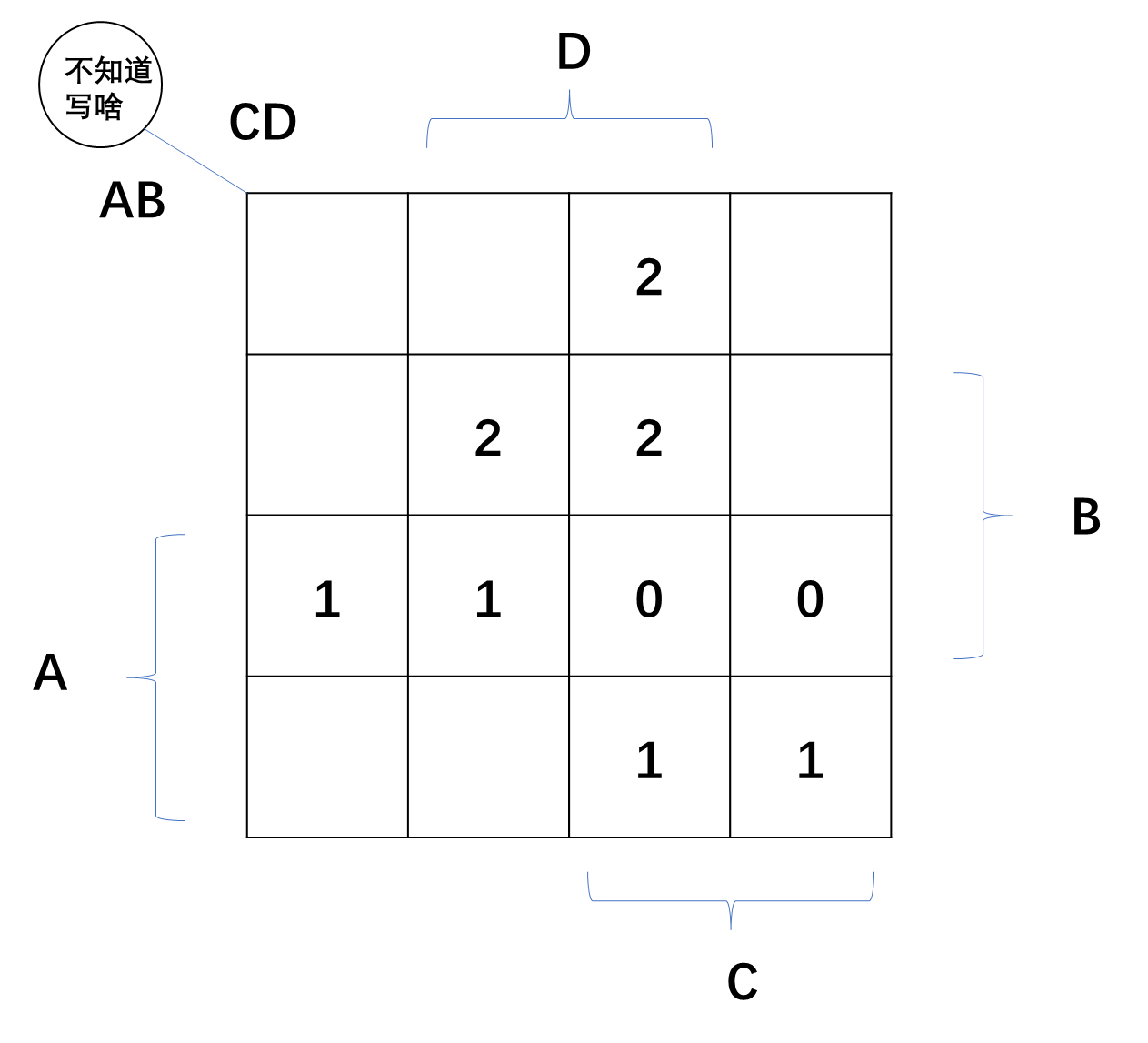
P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)-P(AD)-P(BC)-P(BD)

P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)-P(AD)-P(BC)-P(BD)-P(CD)

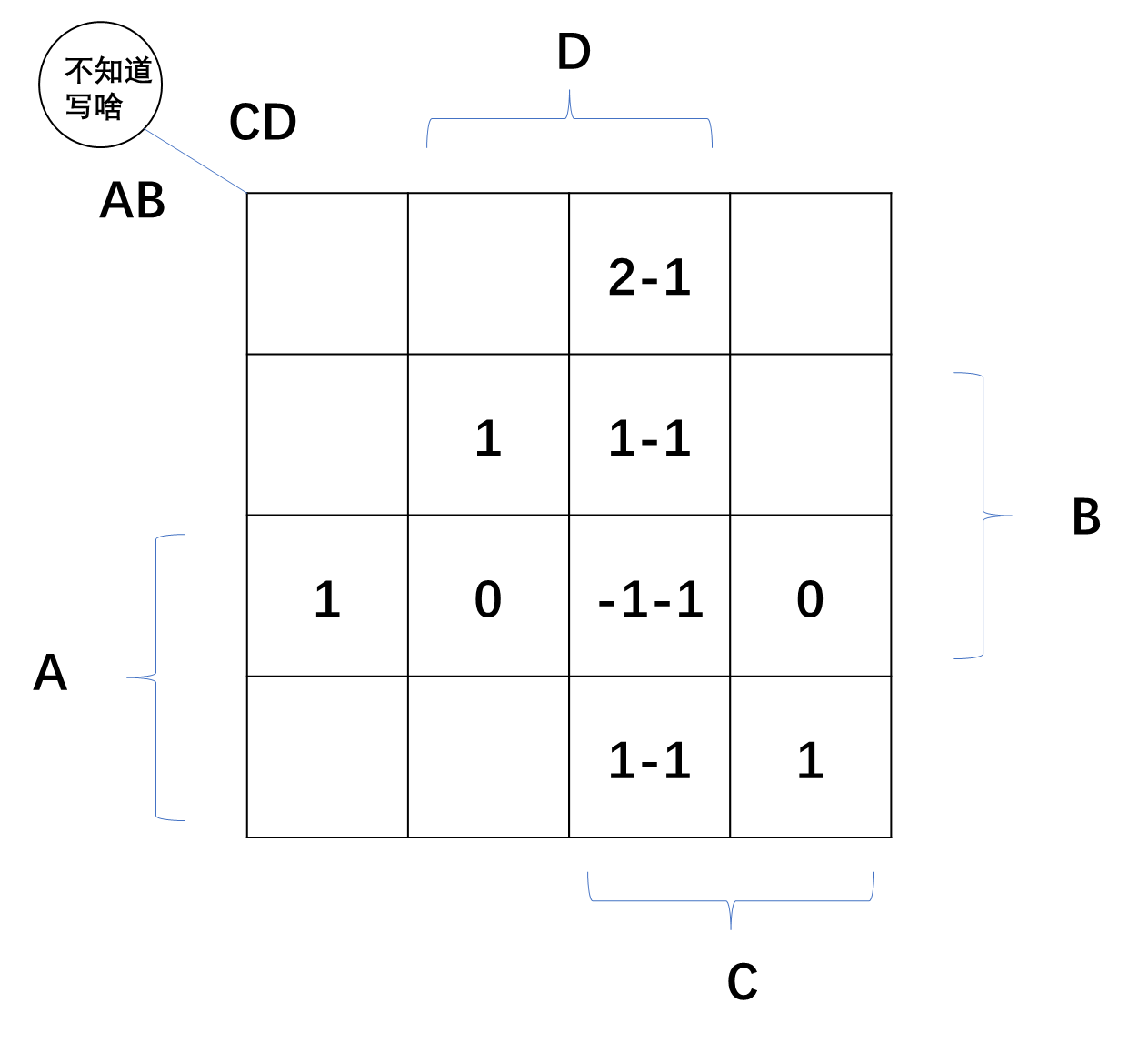
P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)-P(AD)-P(BC)-P(BD)-P(CD)+P(ABC)

P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)-P(AD)-P(BC)-P(BD)-P(CD)+P(ABC)+P(ABD)

P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)-P(AD)-P(BC)-P(BD)-P(CD)+P(ABC)+P(ABD)+P(ACD)

P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)-P(AD)-P(BC)-P(BD)-P(CD)+P(ABC)+P(ABD)+P(ACD)+P(BCD)

P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)-P(AD)-P(BC)-P(BD)-P(CD)+P(ABC)+P(ABD)+P(ACD)+P(BCD)-P(ABCD)

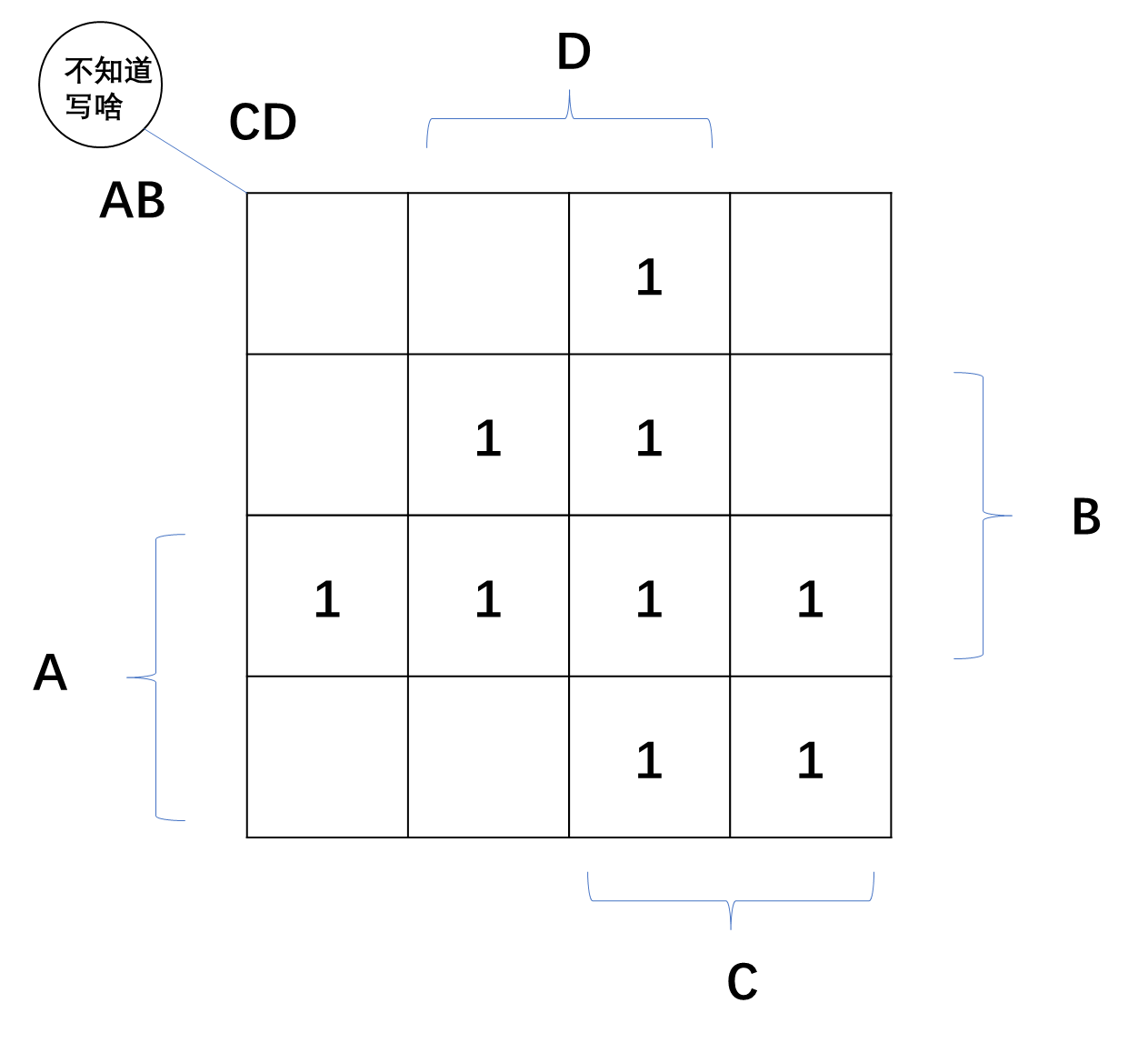
按照公式的顺序瞎整一通刚好可以把每块重叠部分的块数变成1了.

现在我就可以臭不要脸地说这个公式是对的了.

P(A+B+C+D)=P(A)+P(B)+P(C)+P(D)-P(AB)-P(AC)-P(AD)-P(BC)-P(BD)-P(CD)+P(ABC)+P(ABD)+P(ACD)+P(BCD)-P(ABCD)