【动规】子序列问题

前言

动态规划的核心设计思想是数学归纳法

• 本文主要涉及的均为子序列问题，由于认识还是太浅，所以只包含①递增子序列，②公共子序列，两种类型题目。(回文子序列相关问题可看上一篇博客)

题目

300. 最长递增子序列

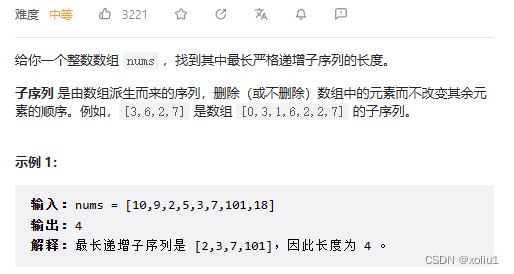
这是一道很入门的题目，有更快的二分解法，但由于我们聚焦于动规和递推思想的培养，所以我在这里只说DP做法。

• 我们令dp[i] 表示选取点 i 能组成的最长递增子序列长度
• 所以我们只需要每次遍历这个点之前的点，判断点 i 是否大于之前的点的值，如果大于就代表可以选点 i 作为最大递增子序列的末尾，更新 dp[i] 为这个最大值。
• 然后我们在每次确定dp[i]，即每一个以 i 为末尾的递增子序列的长度时，都进行一次取max，就能得到最长的递增子序列
• 边界问题处理：每一个独立的数，都是一个长度为1的递增序列。Arrays.fill(dp, 1);

public int lengthOfLIS(int[] nums) {
    int[] dp = new int[nums.length];
    int ans = -1;
    Arrays.fill(dp, 1);
    for (int i = 0; i < nums.length; ++i) {
        for (int j = 0; j < i; ++j) {
            if (nums[i] > nums[j]) {
                dp[i] = Math.max(dp[i], dp[j] + 1);	
                //dp[j] + 1 表明 j 所在的递增子序列
            }
        }
        ans = Math.max(dp[i], ans);
    }
    return ans;
}

673. 最长递增子序列的个数

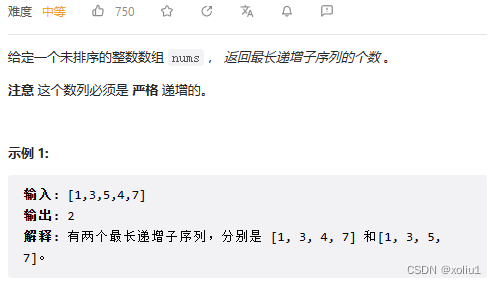
这道题目和上一道题目很相似，但又大为不同，看起来要麻烦许多，但我们的思路不变，因为本质还是递增子序列的问题，所以思考的方向也不变，转移方程也不变。

• 因为我们要求的是数目，那么我们很有必要去定义一个数组cnt[i]，去记录以 i 为末尾的最长递增子序列的个数。
• 我们怎么确定最长呢？其实就是需要我们上一道题一样的思路，确定长度，然后看有哪些递增子序列等于该最长长度（maxLen）。①如果等于该maxLen，我们所记录的cnt[i] 就需要加上前边所匹配子序列个数，因为是以 i 为末尾。②如果有递增子序列比这个长度还要长，那我们更新长度，并且重置 cnt[i] 为 前边的子序列的个数。即：

	if (nums[i] > nums[j]) {
	   if (dp[i] < dp[j] + 1){
	       dp[i] = dp[j] + 1;
	       cnt[i] = cnt[j];
	   }else if(dp[j] + 1 == dp[i]){
	       cnt[i] += cnt[j];
	   }
	}

• 求出 dp[i] 和 cnt[i]，我们对 dp[i] 判断是否是目前为止知道的最长的序列，是的话，我们加上cnt[i],进行更新，不是的话，我们不用管。
• 边界问题：每个单独的个体数，都是长度为1的递增子序列，且数目为1

public int findNumberOfLIS(int[] nums) {
    int[] dp = new int[nums.length];
    int[] cnt = new int[nums.length];
    int ans = 0;
    int mx = Integer.MIN_VALUE;
    for (int i = 0; i < nums.length; ++i) {
        cnt[i] = 1;
        dp[i] = 1;
        for (int j = 0; j < i; ++j) {
            if (nums[i] > nums[j]) {
                if (dp[i] < dp[j] + 1){
                    dp[i] = dp[j] + 1;
                    cnt[i] = cnt[j];
                }else if(dp[j] + 1 == dp[i]){
                    cnt[i] += cnt[j];
                }
            }
        }
        if(dp[i] > mx){
            mx = dp[i];
            ans = cnt[i];
        }else if (dp[i] == mx){
            ans += cnt[i];
        }
    }
    return ans;
}

646. 最长数对链

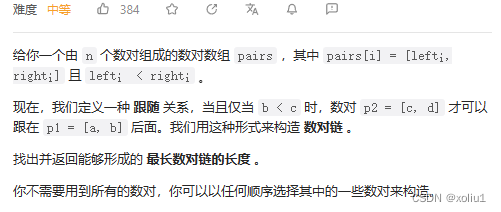
很简单，不必多说，没有要求子序列，只要求链，我们可以进行排序。思想和前面的题一样。没啥说的。

public int findLongestChain(int[][] pairs) {
    if (pairs.length == 0 || pairs[0].length == 0){
        return 0;
    }
    Arrays.sort(pairs, new Comparator<int[]>() {
        @Override
        public int compare(int[] o1, int[] o2) {
            return o1[0] - o2[0];
        }
    });
    int[] dp = new int[pairs.length + 1];
    Arrays.fill(dp, 1);
    for (int i = 1; i < pairs.length; ++i) {
        for (int j = 0; j < i; ++j) {
            if (pairs[j][1] < pairs[i][0]){
                dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
    }
    int mx = -1001;
    for (int i = 0; i < dp.length; ++i) {
        mx = Math.max(mx, dp[i]);
    }
    return mx;
}

1218. 最长定差子序列

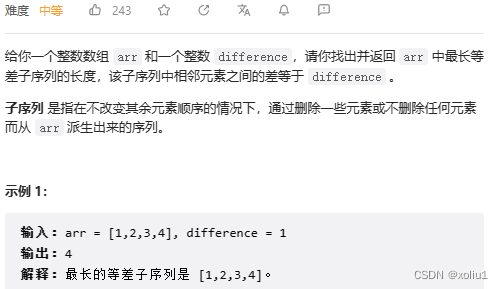
• 有了前面的题目的经验，我们是不是就可以先判断前边有无子序列差值为 k ，然后同样的转移方程呢？
• 按理来说可以，但那是O(n2)的算法，在这个题目中会超时，所以我们需要寻求其他更加巧妙地算法。
• 优化总是从暴力变简单，我们想，每次都是需要往前边遍历去寻找是否有一个具体的值，为什么说是一个具体的值呢？如果我们走到arr[i] = 4,定差为1，那么根据我们原本的写法是需要找一个值，即：arr[j] + differece == arr[i] ，arr[i], difference 均已知，我们就是需要在前面统计过的值中找一个 ‘3’
• 这就让我们想到哈希表，哈希表可以在 O(1) 内找到是否有该具体值，我们可以用 键 表示一个对应的数组值，而 值 就可以像之前定义的dp数组的含义一样，这样一来，我们之前的dp数组还在，只不过换了另一种形式罢了。
• 如果不需要修改原数组的值，直接用迭代器会更快。

    public int longestSubsequence(int[] arr, int difference) {
        if (arr.length < 2){
            return arr.length;
        }
        int mx = -1001;
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i : arr) {
            map.put(i, map.getOrDefault(i - difference, 0) + 1);
            //如果存在该等差项的前一项，那么给这个次数加1
            mx = Math.max(mx, map.get(i));
            //更新最大值
        }
        return mx;
    }

1143. 最长公共子序列

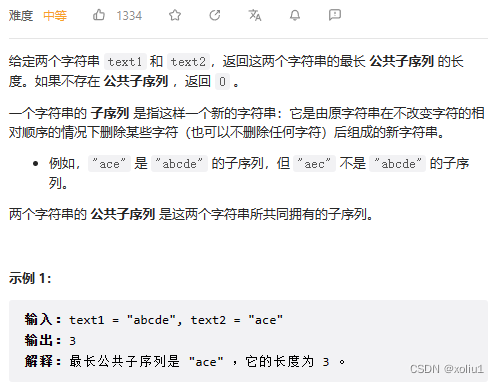
经典的两个字符串之间的问题

• 我们定义dp[i][j]表示 s1的前 i 个字符到s2的前 j 个字符的最大公共子序列长度
• 当s1[i] == s2[j] 时表示s1的第i个字符等于s2的第j个字符, 这时最长公共子序列可以来自s1 前i - 1个字符与s2前j - 1个字符构成的最长公共字符串（已经推出来的），再加上 1
• 当s1[i]] != s2[j] 时 则s1的前i个字符到s2的前j个字符的最公共大子序列可以等于 dp[i-1][j] 或者 dp[i][j-1] 中任意一个，我们求最大值即可。

public int longestCommonSubsequence(String text1, String text2) {
    int[][] dp = new int[text1.length() + 1][text2.length() + 1];
    for (int i = 1; i <= text1.length(); ++i) {
        for (int j = 1; j <= text2.length(); ++j) {
            if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[text1.length()][text2.length()];
}

1035. 不相交的线

public int maxUncrossedLines(int[] nums1, int[] nums2) {
    int[][] dp = new int[nums1.length + 1][nums2.length + 1];
    //含义为数组A的前i项和数组B的前j项的不相交的线的个数
    for (int i = 1; i <= nums1.length; ++i) {
        for (int j = 1; j <= nums2.length; ++j) {
            if (nums1[i - 1] == nums2[j - 1]){
                dp[i][j] = dp[i - 1][j - 1] + 1;
            }else{
                dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
            }
        }
    }
    return dp[nums1.length][nums2.length];
}

其实就是求最长公共子序列