A:XP的字符画
题目描述
XP对字符画情有独钟,他喜欢用字符组成各种不同的图案。请帮XP写一个程序,在屏幕中显示2018,样例如下
#include<stdio.h>
#define p printf
int main()
{
p("*** *** *** ***\n");
p(" * * * * * *\n");
p("*** * * * ***\n");
p("* * * * * *\n");
p("*** *** *** ***\n");
return 0;
}B:XP的楼梯
题目描述
XP是个淘气的孩子,他最近迷上了跳楼梯。他可以一次跳一级,也可以一次跳两级,他居然还能够一次跳三级楼梯(危险动作,请勿模仿)。某次,XP在跳完楼梯后突然想到一个问题,如果有n级楼梯,他从第一级开始往上跳,一直跳到第n级共有多少种不同的方案?你能帮他解决这个问题吗?当然,如果只有一级楼梯,很明显他只有一种选择。
输入
单组输入数据 n (0<n<30)
输出
输出一行结果
样例输入 Copy
29样例输出 Copy
15902591
#include<stdio.h>
int fun(int n)
{
int a[31]={0};
a[1]=1;
a[2]=1;
a[3]=2;
for(int i=4;i<=n;i++)
a[i]=a[i-1]+a[i-2]+a[i-3];
return a[n];
}
int main()
{
int n;
scanf("%d",&n);
printf("%d\n",fun(n));
return 0;
}C:简单的几何学
题目描述
这是一个十分简单的几何学题目。现在给出N个点的坐标(x,y),保证x和y都是整数,你的任务是判断这N个点是否能构成正N边形。
输入
单组输入数据
第一行是N,(2<N<1000)
接下来有N行,每行两个数,代表这个点的坐标(x,y)
−1000≤x,y≤1000 且保证都为整数
输出
输出一行结果
如果可以构成正N边形,输出Yes,否则输出No样例输入 Copy
4 0 50 0 -50 50 0 -50 0样例输出 Copy
Yes
#include <stdio.h>
int a[1005],b[1005],c[1005];
double fun(int x1,int y1,int x2,int y2)
{
return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
}
int main(){
int n;
scanf("%d",&n);
if(n!=4){
printf("No\n");
}
else{
for(int i=0;i<n;i++){
scanf("%d%d",&a[i],&b[i]);
}
int k=0;
for(int i=0;i<n;i++){
for(int j=0;j<i;j++){
c[k++]=fun(a[i],b[i],a[j],b[j]);
}
}
for(int i=0;i<6;i++){
for(int j=0;j<6-1-i;j++){
if(c[j]>c[j+1]){
int t;
t=c[j];
c[j]=c[j+1];
c[j+1]=t;
}
}
}
if(c[0]==c[1]&&c[1]==c[2]&&c[2]==c[3]&&c[4]==c[5]&&c[4]!=c[0]){
printf("Yes\n");
}
else{
printf("No\n");
}
}
return 0;
}D:高中数学
题目描述
今天新生赛,zc做题做到一半做不出来了,索性写起了打油诗
“到这个水平应该就算入门了吧”,zc说道。真不巧,这句话就被lyg听到了,作为高考数学130的男人,他可不能忍,“这能算入门?GCD可是高中的内容,辗转相除,又名欧几里德算法(Euclidean algorithm),它是已知最古老的算法, 其可追溯至公元前300年。它首次出现于欧几里德的《几何原本》(第VII卷,命题i和ii)中,而在中国则可以追溯至东汉出现的《九章算术》”,看着lyg说完,zc有些不服气,“有本事你来写一个瞧瞧~”。
而作为高中数学同样优秀的你,写个GCD完全不成问题
输入
单组输入数据,一行两个整数
(0<a,b<109)输出
输出一行结果,代表a和b的最大公约数
样例输入 Copy
123456 7890样例输出 Copy
6
#include<stdio.h>
int fun(int a,int b){
if(a==0)
return b;
return fun(b%a,a);
}
int main()
{
int a,b;
scanf("%d%d",&a,&b);
printf("%d\n",fun(a,b));
}E:高中生物学
题目描述
“作为刚从高中步入大学的学霸,考我孟德尔遗传定律?呵,又是一道送分题”,电脑前的参赛选手笑着说道。
孟德尔在修道院后院种植豌豆时,发现并总结出了两条规律,后人称之为孟德尔定律。他在1856年至1863年间种下了约5000株豌豆植株并进行杂交实验,随后于1865年在布吕恩自然科学研究协会上报告了他的研究结果,1866年他又发表了论文《植物杂交试验》(德语:Versuche über Pflanzen-Hybriden)。——维基百科
从孟德尔的碗豆杂交实验可以得出以下结论:
- 亲代父本与母本体内各有一成对因子(基因)可决定遗传特征。
- 此一成对因子在杂交的过程中会分开,重新进行组合。(第一定律)
- 不同遗传特征的基因独立而不互相干扰。(第二定律)
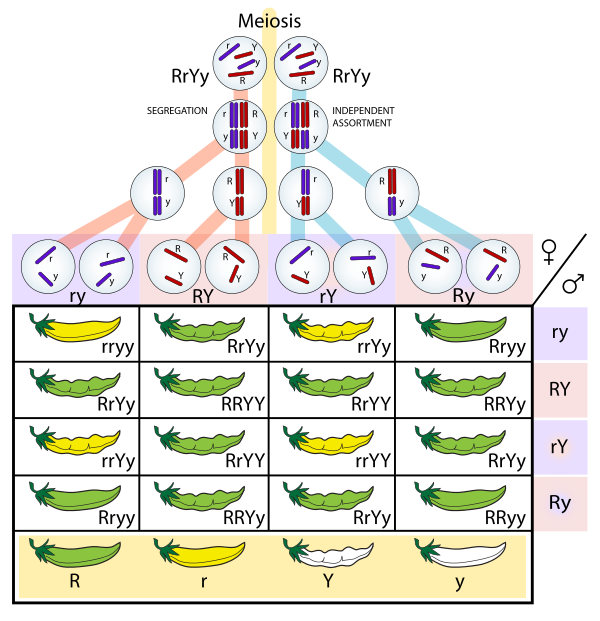
现在给你父本和母本的两对基因,你可以计算出其子代出现某一种基因组合的概率吗?
输入
单组输入数据
一行三组基因,每组基因格式固定为两对基因AaBb,不会出现其他字母
前两组代表其亲代父本和母本的基因,第三组代表子代的基因
输出
输出子代出现此基因的概率,用最简分数表示,概率为0或1则直接输出0或1
样例输入 Copy
AABb Aabb AaBb样例输出 Copy
1/4
#include<stdio.h>
#include<string.h>
char s1[50],s2[50],s3[50],s[16][50];
void swap(char *a, char *b) {
char t = *a;
*a = *b;
*b = t;
}
int main(){
int cnt;
scanf("%s%s%s",s1,s2,s3);
for(int i=0;i<2;i++){
for(int j=2;j<4;j++){
for(int k=0;k<2;k++){
for(int z=2;z<4;z++){
sprintf(s[cnt], "%c%c%c%c", s1[i], s2[k], s1[j], s2[z]);
cnt++;
}
}
}
}
for(int i=0;i<16;i++){
if(s[i][0]>s[i][1]){
swap(&s[i][0],&s[i][1]);
}
if(s[i][2]>s[i][3]){
swap(&s[i][2],&s[i][3]);
}
}
cnt=0;
for(int i=0;i<16;i++){
if (strcmp(s[i], s3) == 0) {
cnt++;
}
}
if(cnt==4) printf("1/4\n");
else if(cnt==0) printf("0\n");
else if(cnt==16) printf("1\n");
else if (cnt == 2) printf("1/8\n");
else if (cnt == 6) printf("3/8\n");
else if (cnt == 8) printf("1/2\n");
else if (cnt == 10) printf("5/8\n");
else if (cnt == 12) printf("3/4\n");
else if (cnt == 14) printf("7/8\n");
else printf("%d/4\n",cnt);
return 0;
}E:初中化学
题目描述
能够进入湖南中医药大学这样的高等院校,我相信你对单质铁与硫酸铜的置换反应并不陌生,我们依稀记得要分成三种情况讨论
- 单质铁过量
- 硫酸铜溶液过量
- 恰好反应完
既然我们现在已经是大学生了,我们应该学会使用成熟的方法来解决问题。
Fe+CuSO4⟹FeSO4+Cu
假设现在有x克单质铁,y克质量分数为z%的硫酸铜溶液,现将单质铁放入装有硫酸铜溶液的烧杯中,待充分反应后,将此烧杯称重(烧杯重50g),你能写出一个程序自动计算称重的结果吗?
可能用到的相对原子质量如下:
符号 相对原子质量 O 16 S 32 Fe 56 Cu 64
输入
单组输入数据
x y z(0<x,y<10000,0<z<100)(0<x,y<10000,0<z<100),保证x和y都为整数
输出
输出一行,代表称重的结果(保留整数)。
样例输入 Copy
56 1635 4.68样例输出 Copy
1741
#include<stdio.h>
int main(){
double z;
int x,y;
scanf("%d%d%lf",&x,&y,&z);
printf("%d\n",x+y+50);
return 0;
}



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








