C语言之循环的嵌套

• 三种循环语句可互相嵌套，层数不限。
• 外层循环可包含两个以上内循环，但不能相互交叉。
• 嵌套的循环控制变量不能相同。

例1.编程求解1！+2!+……...+10!

问题分析：

采用双重for循环，整体共有10部分，对每一部分分别求阶乘。定义变量m用来存储每一部分的阶乘，sum用来存储各个部分之和。每次求阶乘后，m的值都会发生变化，所以在每部分进行阶乘前，需要对m重新赋值。所以m=1，需要放在第一重循环中，第二重循环前。

 代码如下：
#include<stdio.h>
void main()
{
   int i,j,sum=0,m;
   for(i=1;i<=10;i++)
      {
        m=1;
        for(j=1;j<=i;j++)
            m=m*j;
        sum=sum+m;
       }
    printf("结果是：%d",sum);
}

例2.打印输出如下所示左下三角形式的九九乘法表。

 问题分析：

根据计算机输出操作的特点，考虑采用双重for循环实现逐行输出每一列乘法表达式。

1.对乘法表进行整体分析。输出的乘法表共占9行，每一行表达式的个（列）数等于行数。因此，设定两个整型变量i和j，分别代表行号和列号则i∈[1,9],j∈[1,i]。

2.对每行每列的乘法表达式进行逐个分析，第i行第j列乘法表达式的被乘数等于行号i，乘数等于列号j。

3.为了实现图片中的排列形式，故每一行结束后，都需要换行。即第一重循环每进行一次，就需要输出一次换行符。

代码如下：

#include<stdio.h>
void main()
{
   int i,j;
   for(i=1;i<=9;i++)
      {
        for(j=1;j<=i;j++)
            printf("%d*%d=%d ",i,j,i*j);
         printf("\n");
       } 
}

例3.给定1、2、3、4四个数字，输出所有由它们构成的无重复数字的三位数。

问题分析：

本例在1、2、3、4四个数字构成的三位数中找出那些无重复数字的三位数，这是典型的可以用穷举法求解的问题。三位数的百位、十位、个位都允许填入这4个数字。每一位用一个循环语句实现，则需要三层循环的嵌套，第一层测试百位，第二层测试十位，第三层测试个位，每一层循环4次。若用循环变量i，j，k分边表示百位、十位和个位的数字，则每个循环变量的取值是1、2、3、4。在最里层循环中，条件(i!=j&&i!=k&&j!=k)满足了题中的要求（无重复数字），表达式i*100+j*10+k形成了一个三位数。

 代码如下：

#include<stdio.h>
void main()
{
   int i,j,k;
   for(i=1;i<=4;i++)
      for(j=1;j<=4;j++)
         for(k=1;k<=4;k++)
            if(i!=k&&i!=j&&j!=k)
            printf("%d%d%d ",i,j,k);
}

例4.实现以下图形的输出。

问题分析：

观察图形，找出规律。定义行数i，空格随着行数增加，每次减一。星号随着行数增加，有2i-1的规律。通过第一重循环来控制行数，通过两个并列的循环，分别来控制空格和星号。

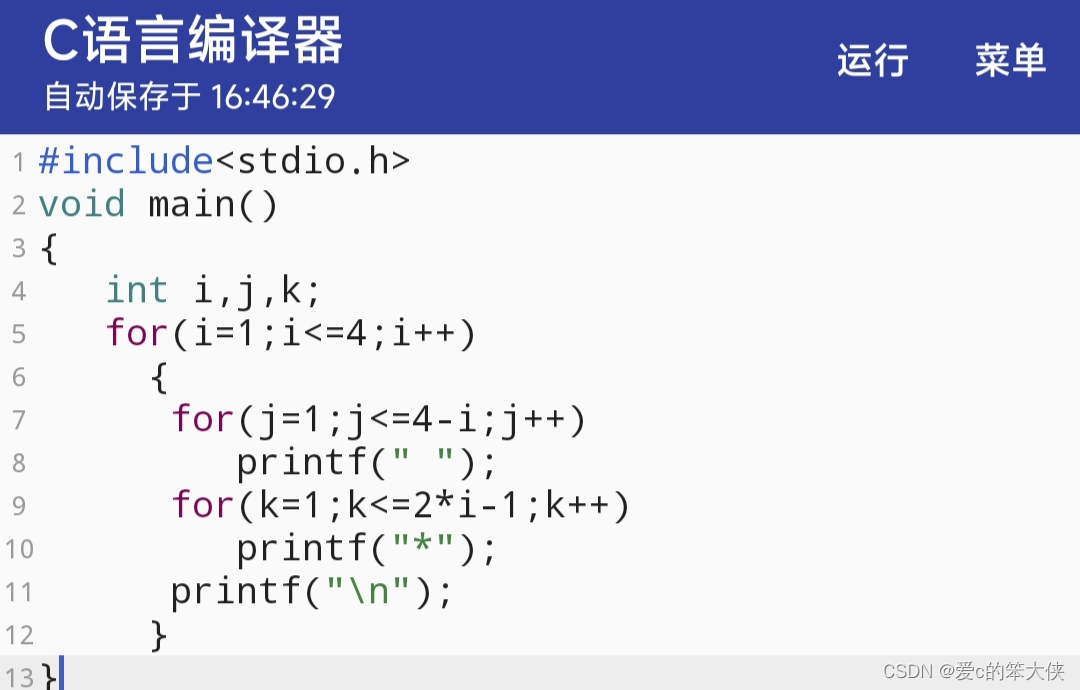
代码如下：

#include<stdio.h>
void main()
{
   int i,j,k;
   for(i=1;i<=4;i++)
     {
      for(j=1;j<=4-i;j++)
         printf(" ");
      for(k=1;k<=2*i-1;k++)
         printf("*");
      printf("\n");
     }
}

例5.用循环的嵌套编程实现输出所有的“水仙花数”。

问题分析：

如果要用循环的嵌套来实现，我们自然的就可以想到用三个循环来表示百位，十位，个位。进而表示100到999之间的所有数。

代码如下：

#include<stdio.h>
void main()
{
   int i,j,k,n;
   printf("水仙花数是：");
   for(i=1;i<=9;i++)
      for(j=0;j<=9;j++)
          for(k=0;k<=9;k++)
             {
              n=100*i+10*j+k;
              if(n==i*i*i+j*j*j+k*k*k)
                printf("%d ",n);
              }  
}

对比：

求水仙花数需要得知两个条件：某个数 和 这个数的个，十，百位。如果通过循环，则可以得到所有三位数，故通过三位数求每个位上的数。而循环的嵌套，则是先得知每个位上的数，来求所有的三位数。