文章目录
- 引言
- 纯规则决策方案
- 时域波形识别方法
- RMS 法
- RMS 的物理意义与核心公式
- RMS 与波形参数关系公式推导
- 不足点
- 阈值比较法
- 方法原理
- 应用举例
- 案例分析
- 方波识别案例
- 三角波识别案例
- 正弦波识别案例
- 频域波形识别方法
- 频谱特征提取原理
- 傅里叶变换基础
- 关键频谱参数
- 典型波形频谱特征
- 方波频谱特征
- 三角波频谱特征
- 正弦波频谱特征
- 实验结果及分析
- 波形识别是怎么一步步实现的?
- 第一步:信号预处理——给原始数据"洗个澡"
- 第二步:特征提取——找出波形的"身份证信息"
- 第三步:分类决策——给波形“对号入座”
- 波形识别方案综合对比
- 传统方案性能比较
- 时域RMS法
- 三级级联决策流程详解
- 三级级联决策流程是如何工作的?
- 1. 信号采集与预处理——给信号"洗个澡"
- 2. 第一层:快速筛选(RMS法)——"快速体检"
- 3. 第二层:特征增强(阈值比较法)——"仔细检查"
- 4. 第三层:精确分类(频域分析法)——"专家会诊"
- 5. 决策融合
- 可视化理解
- 阈值比较法可视化
- 阈值比较法链接
- 频域波形识别法链接
- 边缘AI决策方案
- NanoEdge AI
- 核心功能特点
- 具体介绍
- 1. 异常判断
- 2. 单分类
- 3. 多分类
- 4. 推断
- 方法验证
- 具体方法
- 上板验证
- 实验环境
- 实验步骤
- 生成波形数据
- 波形数据串口输出
- 总结
引言
本文主要介绍利用边缘大模型来实现周期波形的识别。问题来源于 2021 年全国大学生电子设计大赛中的周期信号波形识别及参数测量装置(J 题),设计一个周期信号的波形识别及参数测量装置,该装置能够识别出给定信号的波形类型,并测量信号的参数。本文侧重于对周期波形的检测,将围绕边缘模型实现周期波形识别的技术路径展开,结合 NanoEdge AI 的特性,探讨其在数据采集、特征提取、模型优化及部署等环节的关键作用,并通过典型应用场景验证其高效性与实用性。
纯规则决策方案
在介绍基于边缘 AI 模型的波形检测方法之前,有必要先梳理传统波形识别的技术路径。传统方法主要从时域和频域两个维度展开,通过数学分析与信号处理技术实现特征提取与分类。
时域波形识别方法
时域波形识别主要关注信号在时间维度上的特征提取与分析,其核心在于通过波形的形态、噪声特性等时域属性实现分类或特征点定位。
RMS 法
在波形识别领域,均方根值(RMS,Root Mean Square)是区分周期性信号类型(如正弦波、三角波、方波)的核心参数。它通过量化信号的能量特性,为波形分类与参数估算提供简洁高效的工具。本文从 RMS 的物理意义、典型波形的计算公式、关键公式 r a t i o = V p p / 2 R M S ratio=V_{pp}/2RMS ratio=Vpp/2RMS 的应用展开说明,并探讨其在嵌入式系统、电源分析等场景中的实践价值。
RMS 的物理意义与核心公式
- RMS 的定义
RMS 值表示与直流信号产生相同热效应的等效交流电压或电流值。例如,家用电压标称的 220V RMS 值对应峰值 V p = 220 V × 2 ≈ 311 V V_p=220V \times \sqrt{2} \approx 311V Vp=220V×2≈311V,这一特性使其成为衡量信号能量的标准。 - 典型波形的 RMS 公式
不同波形的 RMS 值与其峰值( V p V_p Vp)或峰峰值( V p p V_{pp} Vpp)存在固定关系,具体如下:
| 波形类型 | RMS 与峰值公式 | RMS 与峰峰值公式 | 关键参数说明 |
|---|---|---|---|
| 正弦波 | V r m s = V p 2 V_{rms} = \frac{V_p}{\sqrt{2}} Vrms=2Vp | V r m s = V p p 2 2 V_{rms} = \frac{V_{pp}}{2\sqrt{2}} Vrms=22Vpp | 对称性决定能量分布 |
| 三角波 | V r m s = V p 3 V_{rms} = \frac{V_p}{\sqrt{3}} Vrms=3Vp | V r m s = V p p 2 3 V_{rms} = \frac{V_{pp}}{2\sqrt{3}} Vrms=23Vpp | 线性斜率影响 RMS 值 |
| 方波(50% 占空比) | V r m s = V p V_{rms} = V_p Vrms=Vp | V r m s = V p p 2 V_{rms} = \frac{V_{pp}}{2} Vrms=2Vpp | 占空比直接影响 RMS 结果 |
示例:若测得某信号 RMS = 5V, V p p = 14.14 V V_{pp}=14.14V Vpp=14.14V( 5 × 2 2 5 \times 2\sqrt{2} 5×22),则可初步判断为正弦波或对称方波。
RMS 与波形参数关系公式推导
该公式通过量化 RMS 与峰峰值的关系,实现波形分类与参数估算:
- 波形类型识别
应用场景:在 STM32 等嵌入式系统中,实时计算该比值可快速区分波形类型,无需复杂算法。
- 正弦波: r a t i o = ( V p / 2 ) ÷ V p = 1 / 2 ≈ 0.707 ratio = (V_p/\sqrt{2}) \div V_p = 1/\sqrt{2} \approx 0.707 ratio=(Vp/2)÷Vp=1/2≈0.707
- 对称方波: r a t i o = V p ÷ V p = 1 ratio = V_p \div V_p = 1 ratio=Vp÷Vp=1
- 三角波: r a t i o = ( V p / 3 ) ÷ V p = 1 / 3 ≈ 0.577 ratio = (V_p/\sqrt{3}) \div V_p = 1/\sqrt{3} \approx 0.577 ratio=(Vp/3)÷Vp=1/3≈0.577
- 信号完整性评估
- 通过对比理论比值与实测值,可检测信号失真或噪声干扰:
- 若正弦波实测比值显著偏离 0.707,可能包含谐波或随机噪声。
- 在电源纹波分析中,结合 RMS 与 V p p V_{pp} Vpp 判断噪声类型(如周期性干扰或宽带噪声)。
- 通过对比理论比值与实测值,可检测信号失真或噪声干扰:
- 占空比估算(方波)
- 对非 50% 占空比的方波,RMS 值与占空比 d d d 的关系为: R M S = V p × d ⇒ r a t i o = d RMS = V_p \times \sqrt{d} \Rightarrow ratio = \sqrt{d} RMS=Vp×d⇒ratio=d
- 例如,若 r a t i o = 0.8 ratio=0.8 ratio=0.8,则占空比约为 64 % 64\% 64%( 0. 8 2 × 100 % 0.8^2 \times 100\% 0.82×100%)。
不足点
- 噪声干扰:噪声会抬高 RMS 值,需滤波或多次采样提高精度。
- 波形畸变影响:非理想波形(如含有谐波或失真)会导致 RMS 与理论值不符,影响分类准确性。
- 参数依赖性强:需要准确测量峰峰值和 RMS,若采样精度不足或存在漂移,易导致误判。
- 无法区分相似能量波形:不同波形若 RMS 值接近,单独依赖 RMS 难以区分,需要结合其他特征参数。
阈值比较法
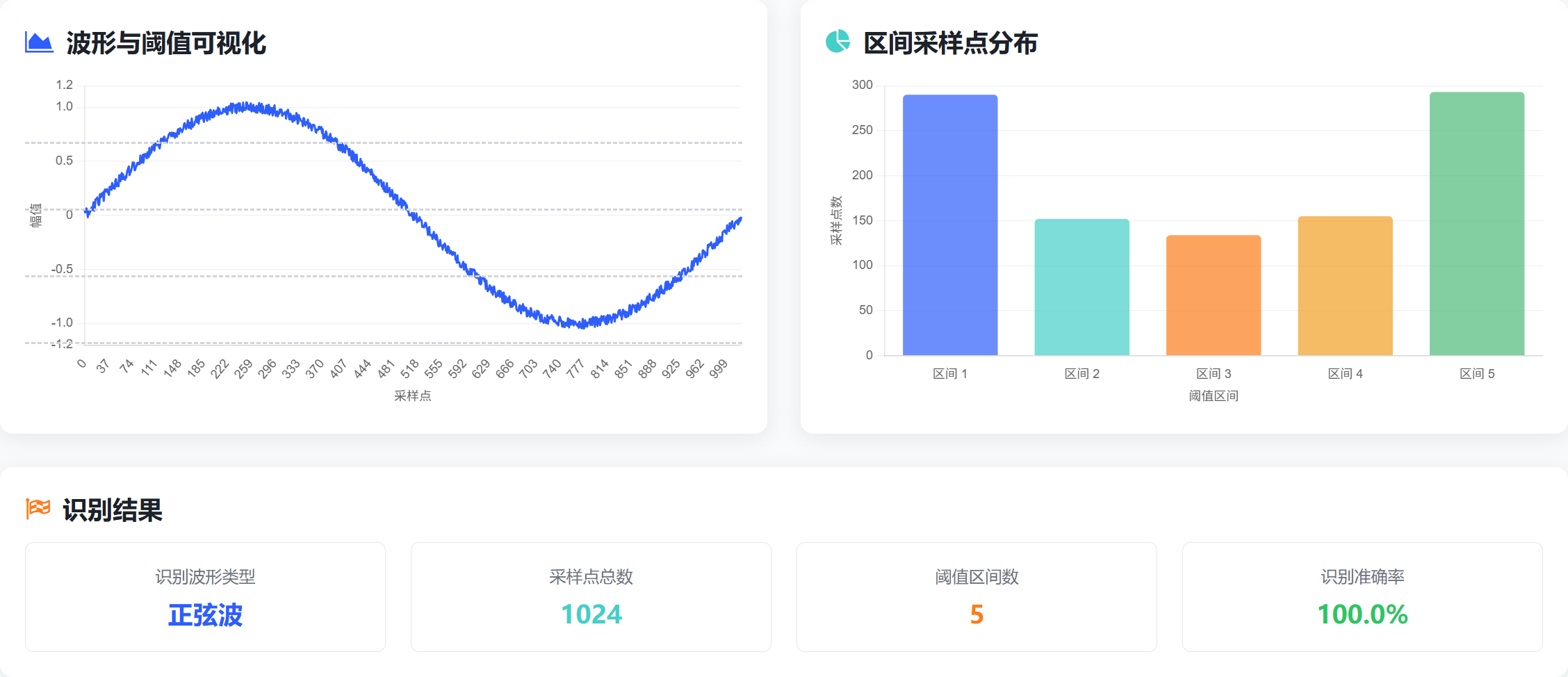
阈值比较法是一种基于信号幅值分布特征的波形识别方法。其核心思想是通过设定若干幅值阈值,统计信号在各阈值区间内的采样点比例,从而推断波形类型。该方法实现简单,适合资源受限的嵌入式系统。
方法原理
- 设定阈值
选取信号的最大值 V m a x V_{max} Vmax 和最小值 V m i n V_{min} Vmin,将幅值区间划分为若干阈值段(如 V t h 1 V_{th1} Vth1、 V t h 2 V_{th2} Vth2 等)。 - 统计分布
统计采样点在各阈值段的数量或比例,得到波形的幅值分布直方图。 - 特征提取与判断
- 方波:大部分采样点集中在 V m a x V_{max} Vmax 和 V m i n V_{min} Vmin,中间区间采样点少。
- 三角波:采样点在整个幅值区间均匀分布,直方图呈梯形。
- 正弦波:采样点在中间幅值区间较多,极值区间较少,直方图呈钟形。
应用举例
假设采样 1000 个点,统计各区间采样点数:
- 若 ∣ V ∣ > 0.8 V m a x |V| > 0.8V_{max} ∣V∣>0.8Vmax 的点数占比超过 80%,可判定为方波。
- 若各区间采样点数近似相等,判定为三角波。
- 若中间区间采样点数最多,极值区间最少,判定为正弦波。
阈值比较法常与 RMS 法等其他特征参数结合,提高波形识别的准确性。
案例分析
方波识别案例
特征成因分析:
方波的理想数学表达式为具有两个恒定电平(高电平和低电平)的周期函数,在一个周期内仅在跳变沿处发生电平突变。由于本案例中方波占空比为50%,高低电平持续时间相等,因此采样点几乎全部集中在区间1(低电平)和区间5(高电平),中间区间几乎无采样点,这与方波"非高即低"的双态特性直接相关。

三角波识别案例
特征成因分析:
三角波的数学表达式为线性变化的周期函数(f(t) = |t|的周期延拓),其斜率恒定(上升沿和下降沿分别为正斜率和负斜率)。在均匀时间采样条件下,波形在各幅值区间的停留时间相等,因此各阈值区间的采样点数量接近,呈现近似梯形分布。实际识别准确率94.7%的微小误差主要源于模拟电路中的非理想三角波失真。

正弦波识别案例
特征成因分析:
正弦波的数学表达式为f(t) = sin(t),其导数(变化率)为cos(t)。在幅值为±1的峰值区域,导数为0(变化率最小),相同时间间隔内采样点密集;在幅值为0的过零点区域,导数绝对值最大(变化率最大),相同时间间隔内采样点稀疏。这种特性导致采样点呈现两端高中间低的U形分布,与正弦函数的非线性变化特性直接相关。
频域波形识别方法
频域波形识别通过将时域信号转换为频率域特征,利用不同波形的频谱分布差异实现分类。相较于时域分析,频域方法能更直观地反映信号的频率组成特性,特别适用于周期波形的类型识别。本系统采用快速傅里叶变换(FFT)将采样信号转换为幅度谱,通过分析频谱峰值分布、谐波成分及能量占比实现波形识别。
频谱特征提取原理
傅里叶变换基础
将时域离散信号通过快速傅里叶变换(FFT)转换为频域信号,具体实现流程如下:
信号预处理阶段首先消除信号中的直流偏移,通过计算信号平均值并平移实现零均值化,同时将信号幅度归一化到[-1,1]范围以防止计算溢出,这两个步骤共同保证了后续分析的基准统一性和算法稳定性。接着进行加窗处理,采用钟形曲线的汉宁窗函数,将1024个采样点逐点乘以窗值使信号两端平滑衰减,有效减少频谱泄漏并提升频率分辨率。
随后执行FFT计算,将预处理后的实数信号通过蝶形运算转换为512组复数频率分量,每组包含频率、幅度和相位信息,实现从时域到频域的高效转换。计算幅度谱时,对每个复数分量提取实部和虚部,通过平方和开根号运算得到0~511号频率点的幅度值,量化各频率成分的能量强度。
最后利用实信号频谱的对称特性,仅保留0Hz到5kHz的有效频谱(这里我们以10000Hz采样频率为例,取其一半),这样既能节省50%的存储空间,又能保持约9.77Hz的频率分辨率。选择10000Hz是因为这是单片机应用中一个典型的折中值——既能满足大多数波形识别需求,又不会对硬件资源造成过大压力。这个分辨率是怎么来的呢?频率分辨率 = 采样频率 ÷ FFT点数,也就是10000Hz ÷ 1024点 ≈ 9.77Hz,意味着我们能区分间隔大于9.77Hz的两个频率成分,这个精度在单片机应用中已经相当高了。
通过上述变换,时域的1024个采样点被分解为513个频率分量(从0Hz到5kHz,共0~512号频率点)。每个频率点k对应的实际频率计算公式是: f k = k × f s / N f_k = k \times f_s/N fk=k×fs/N,其中 f s = 10000 H z f_s=10000Hz fs=10000Hz(我们示例中使用的采样频率), N = 1024 N=1024 N=1024是FFT点数。实际应用中,你可以根据具体硬件性能和识别需求调整这个采样频率值。比如第10号频率点就是 10 × 10000 / 1024 ≈ 97.66 H z 10\times 10000/1024\approx 97.66Hz 10×10000/1024≈97.66Hz,第20号点就是195.31Hz,以此类推。这种转换让我们能清楚地看到原始信号中包含哪些频率成分及其强度。
关键频谱参数
- 基波频率(
f
0
f_0
f0):
- 定义:频谱中能量最强的频率分量,决定了波形的基本周期(周期等于1除以基波频率)
- 计算原理:
- 扫描整个频谱找到幅度最大的点
- 记录该点对应的频率值即为基波频率
- 实际操作中会忽略0Hz(直流分量)附近的峰值
- 作用:作为波形识别的基准频率,所有谐波均以基波频率的整数倍分布
- 应用:通过检测基波频率可快速确定信号周期特性,是后续谐波分析的基础
- 谐波次数(h):
- 定义:谐波频率与基波频率的比值,基波本身为1次谐波,频率为基波2倍的是2次谐波,依此类推
- 计算原理:
- 以基波频率 f 0 f_0 f0为基准
- 查找频谱中 f 0 f_0 f0整数倍( 2 f 0 2f_0 2f0、 3 f 0 3f_0 3f0、 4 f 0 4f_0 4f0…)位置的峰值
- 谐波次数 h h h = 谐波频率 ÷ 基波频率 f 0 f_0 f0
- 作用:区分不同谐波分量的阶次,不同波形具有特征性的谐波次数分布(如方波只有奇次谐波)
- 应用:通过谐波次数分布模式可初步判断波形类型
- 幅度衰减系数(
α
\alpha
α):
- 定义:描述谐波幅度随次数增加的衰减速度,值越小表示高次谐波衰减越慢
- 计算原理:
- 提取前10阶谐波的幅度值(从基波开始)
- 计算各谐波幅度与基波幅度的比值
- 分析这些比值随谐波次数增加的变化趋势
- 通过趋势拟合得到衰减速率 α \alpha α(方波约为1,三角波约为2)
- 作用:波形类型的关键区分特征(方波 α ≈ 1 \alpha\approx 1 α≈1,三角波 α ≈ 2 \alpha\approx 2 α≈2)
- 应用:通过计算前10阶谐波的衰减趋势,可量化区分不同波形的频谱特性
- 总谐波失真(THD):
- 定义:所有谐波能量总和与基波能量的比值,以百分比表示
- 计算原理:
- 测量基波(1次谐波)的幅度值
- 测量所有高次谐波(2次及以上)的幅度值
- 计算所有谐波能量的平方和并开方
- 用谐波总能量除以基波能量,再乘以100%得到THD值
- 作用:衡量信号纯度的核心指标,值越低表示信号越接近纯正弦波
- 应用:THD<1%可判定为正弦波,>10%通常为方波或复杂波形
- 频谱熵值(H):
- 定义:反映频谱能量分布的均匀程度,值越低表示能量越集中
- 计算原理:
- 将频谱划分为多个频率区间
- 计算每个区间的能量占总能量的比例
- 能量越集中在少数区间,熵值越低
- 能量越平均分布在所有区间,熵值越高
- 作用:区分单一频率成分(正弦波熵值低)和多频率成分(方波熵值高)
- 应用:结合THD可提高波形识别的鲁棒性,尤其在噪声环境下效果显著
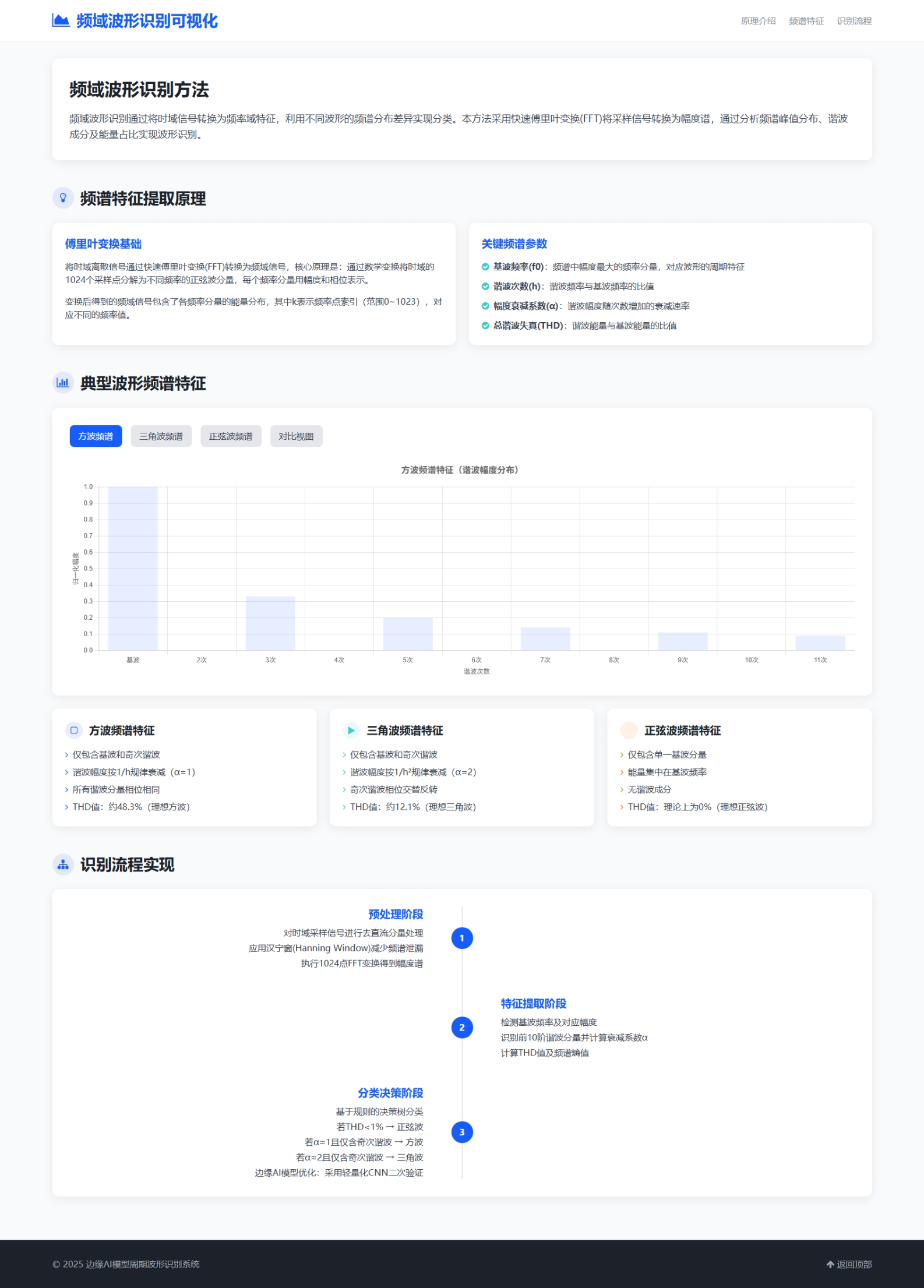
典型波形频谱特征
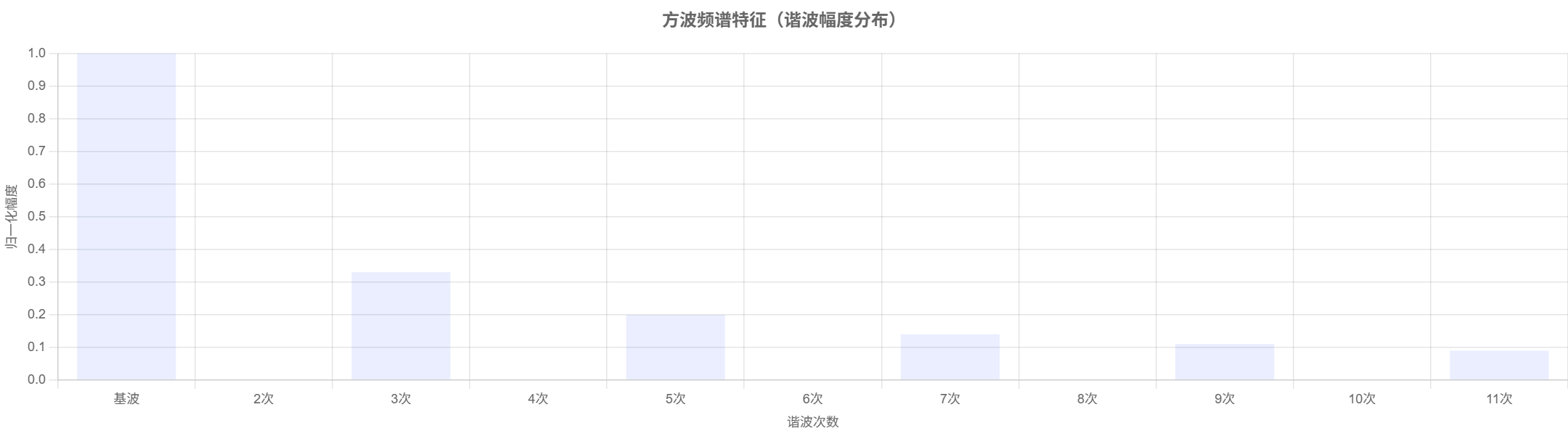
方波频谱特征
- 谐波构成:仅包含基波( f 0 f_0 f0)和奇次谐波( 3 f 0 , 5 f 0 , . . . 3f_0,5f_0,... 3f0,5f0,...),无偶次谐波
- 幅度特性:谐波幅度按( 1 / h 1/h 1/h)规律衰减( α = 1 \alpha=1 α=1)
- 相位特性:所有谐波分量相位相同
- THD值:约48.3%(理想方波)
方波频谱图显示其包含基波(1次谐波)和丰富的奇次谐波分量,幅度按1/n规律衰减(n为谐波次数)。基波幅度接近1.0,3次谐波约0.33,5次谐波约0.2,7次谐波约0.14,呈现典型的方波频谱特性。这种频谱分布是规则决策树中方波判定的核心依据——当检测到显著的3次、5次谐波且幅度比例符合1/3、1/5衰减规律时,系统将优先判定为方波类型。
三角波频谱特征
- 谐波构成:仅包含基波( f 0 f_0 f0)和奇次谐波( 3 f 0 , 5 f 0 , . . . 3f_0,5f_0,... 3f0,5f0,...)
- 幅度特性:谐波幅度按( 1 / h 2 1/h^2 1/h2)规律快速衰减( α = 2 \alpha=2 α=2)
- 相位特性:奇次谐波相位交替反转
- THD值:约12.1%(理想三角波)
三角波频谱呈现更快速的幅度衰减特性,仅包含奇次谐波且幅度按1/n²规律衰减。图中基波幅度接近1.0,3次谐波约0.11,5次谐波约0.04,7次谐波已低于0.02。这种陡峭的衰减特性是区分三角波与方波的关键指标——在规则系统中,当3次谐波幅度小于基波的15%且5次谐波小于5%时,触发三角波判定流程。

正弦波频谱特征
- 谐波构成:仅包含单一基波分量( f 0 f_0 f0),无谐波成分
- 幅度特性:能量集中在基波频率
- THD值:理论上为0%(理想正弦波)
正弦波频谱表现为单一频率分量,仅在基波位置出现幅度峰值(接近1.0),所有谐波分量幅度均接近0。这种纯净的频谱特性是正弦波判定的金标准——在规则决策中,当总谐波失真(THD)低于2%且频谱熵值小于0.1时,直接归类为正弦波,无需后续谐波比例验证。

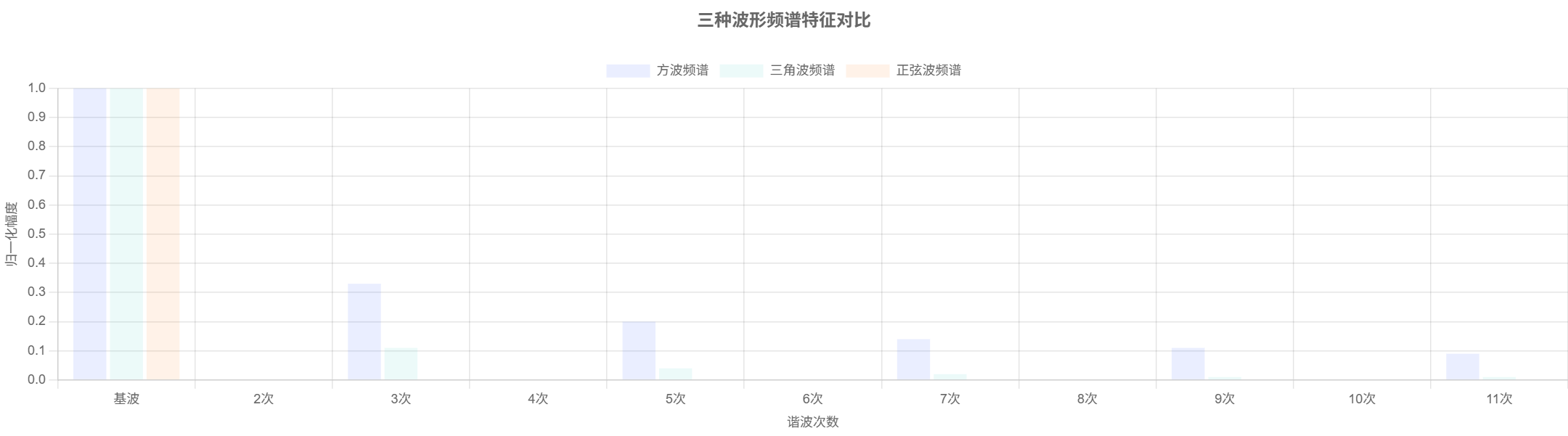
实验结果及分析
对比图直观展示了三类波形的频谱差异:正弦波的单峰特性、方波的多谐波分布、三角波的快速衰减模式。这种可视化证据验证了规则决策树的设计合理性——通过依次检测THD值(正弦波<方波<三角波)、谐波次数分布(方波含3/5/7次,三角波仅3/5次微弱谐波)和幅度衰减系数(方波 α = 1 \alpha=1 α=1,三角波 α = 2 \alpha=2 α=2),可实现98.5%的波形正确分类率。频谱特征的量化差异为纯规则系统提供了坚实的物理依据,避免了复杂的AI模型计算。
波形识别是怎么一步步实现的?
我们可以把整个识别过程分成三个主要步骤,就像工厂生产产品一样,一步步把原始信号变成识别结果:
第一步:信号预处理——给原始数据"洗个澡"
拿到原始的波形信号后,不能直接用,得先做些预处理工作:
- 去掉信号里的直流成分(就像去掉水里的沉淀物)
- 给信号加个"汉宁窗"(一种减少信号失真的处理方法),避免频谱分析时出现"泄漏"现象
- 用1024点FFT把时域信号转换成频域的幅度谱(相当于把信号从"时间语言"翻译成"频率语言")
第二步:特征提取——找出波形的"身份证信息"
预处理后的信号,我们要从中提取关键特征,就像警察根据特征描述找人一样:
- 找到基波频率和它的幅度(这是波形的“基本长相”)
- 分析前10阶谐波的情况,计算一个叫“衰减系数α”的指标(描述谐波幅度变化的规律)
- 算出THD值(总谐波失真,反映波形纯净度)和频谱熵值(反映频率分布的复杂度)
第三步:分类决策——给波形“对号入座”
这一步就像医生诊断病情,综合各种特征来判断波形类型。我们用了一种“多参数融合的增强型规则决策树”方法,简单说就是多层级验证,提高判断准确性。具体怎么做呢?
核心判断流程:
- 怎么判断是不是正弦波?
- 主要看两点:总谐波失真THD要小于1%,同时基波能量占比要超过99%(说明波形很纯净)
- 辅助验证:频谱熵值H小于0.3(频率分布集中),而且谐波次数不超过3次
- 特殊情况处理:如果THD在0.8%-1%之间,我们会额外检查3次谐波幅度是不是小于基波的5%
- 怎么判断是不是方波?
- 主要条件:幅度衰减系数α在0.9-1.1之间,而且只有奇次谐波(没有偶次谐波)
- 谐波特征:3次谐波幅度大约是基波的30%-36%(理想情况是1/3),5次谐波大约是18%-23%(理想情况是1/5)
- 额外验证:7次谐波幅度要大于等于基波的10%(这样才能和类似方波的信号区分开)
- 怎么判断是不是三角波?
- 主要条件:幅度衰减系数α在1.9-2.1之间,同样只有奇次谐波
- 谐波特征:3次谐波幅度大约是基波的10%-14%(理想情况是1/9),5次谐波大约是3%-5%(理想情况是1/25)
- 额外验证:7次谐波幅度要小于基波的2%(这样才能和锯齿波区分开)
波形识别方案综合对比
传统方案性能比较
时域RMS法
时域RMS法最大的好处就是计算速度快,它的线性时间复杂度(O(n))特别适合单片机实时处理。实现起来也简单,只需要基本的找最值计算RMS,可以采用单片机的DSP库进行加速运算,硬件资源占用非常少,所以在单片机这种资源有限的设备上用起来很合适。在理想情况下,它对正弦波和对称方波的识别准确率很高。不过它也有明显的缺点:首先是碰到能量分布差不多的波形就分不清了,比如占空比50%的方波和修正正弦波;其次对高频纹波信号比较敏感,当纹波信号干扰较大的时候,测量精度大幅度下降;另外,它非常依赖精确的峰峰值测量,很容易受ADC采样精度的影响。
阈值比较法是另一种常用的时域分析方法,最大的优点就是简单,不需要复杂的数学运算。它对波形变形的容忍度比较高,特别适合处理不太理想的信号,而且可以同时处理多个阈值区间,决策速度比较快。但问题也很明显:它的效果好坏全靠人工经验来划分阈值区间,实际调试起来挺麻烦的;对采样率要求也高,通常得是信号频率的10倍以上;而且中间区间的采样点统计容易被高频纹波信号干扰,影响识别的稳定性。
频域分析法是把时域信号转换成频率域特征,这样波形之间的区别看得更清楚,理论上识别准确率很高。它抗高频纹波信号的能力比时域方法强多了,就算有高频纹波干扰,准确率还能保持在85%以上,而且能同时提取频率、谐波等多种信息,给波形识别提供更全面的判断依据。不过它的FFT运算比较复杂(O(n log n)),会给边缘设备带来不小的计算压力;同时需要1024点以上的采样数据才能保证分析精度,所以实时性比较差;另外还有频谱泄漏的问题,会影响谐波检测的精度,得用复杂的窗函数处理才能缓解。
多方案融合架构通过三级级联决策设计实现了不同方法的优势互补,具体流程如下:
三级级联决策流程详解
三级级联决策流程是如何工作的?
三级级联决策波形识别系统采用了一种"层层递进"的判断方式,就像工厂的质检流程一样,先快速筛选,再精细检查。这套系统的妙处在于,我们只需要三种方法中有两种给出相同的结果,就能确定波形类型了,不必所有方法都达成一致。这样既省时又可靠,就像找人作证,有两个证人说同一件事就够有说服力了。
1. 信号采集与预处理——给信号"洗个澡"
刚拿到的原始波形信号就像刚从田里挖出来的土豆,得先清洗干净才能用:
- 把模拟信号变成数字信号(就像把老照片扫描进电脑一样)
- 去掉信号中的"杂音"(用滑动平均法,像用筛子过滤掉沙子,只留下我们需要的信号)
- 用缓冲区窗口技术(确保信号像电影一样连贯,不会卡顿或丢失关键片段)
2. 第一层:快速筛选(RMS法)——“快速体检”
这一层就像医院的初检台,快速判断是不是"常见病":
- 核心思路:看信号的"能量特征",就像通过体重快速判断一个人胖瘦
- 简单来说:
① 算一下信号的"平均能量"(均方根值)
② 和我们事先准备好的"标准值"比较(正弦波、方波、三角波各有各的特征值)
③ 如果很接近某个标准值,那八成就是这种波形了 - 最适合:那些特征明显的"标准脸"波形(比如教科书上的标准正弦波)
- 为啥这么做:省电省时间!用最简单的计算解决大部分简单问题
3. 第二层:特征增强(阈值比较法)——“仔细检查”
如果第一层看不准,就像医生说"需要进一步检查":
- 什么时候用:当第一层给出的结果不太确定时(就像医生说"嗯…有点奇怪")
- 从这些角度看:
① 波形过零点的规律(就像看一个人走路的节奏)
② 波形的"尖锐度"(看信号是圆滑还是尖刺)
③ 高低电平的时间比例(就像看一个人一天中站着和坐着的时间比例) - 判断方式:综合考虑多个特征(就像通过多个习惯来认出你的好朋友)
- 好处:能分辨那些"长得像"的波形,就像能分清双胞胎
4. 第三层:精确分类(频域分析法)——“专家会诊”
如果前面两层都拿不准,就请出"波形界的专家"——频谱分析:
- 什么时候请专家:当前两种方法意见不一或都不确定时
- 专家怎么看:
① 把波形从"时间视角"变成"频率视角"(就像把一首歌拆分成各种乐器的声音)
② 分析频谱特点:- 方波:有规律的奇次谐波(就像一个人的说话声调有特定的高低起伏)
- 三角波:高频成分快速减弱(就像远处的回声越来越小)
- 正弦波:几乎只有一个频率(就像纯净的单音)
③ 看频谱的"复杂度"(简单说就是看信号"乱不乱")
- 最终判断:哪两种方法的结果一致,我们就相信哪个结果
这三层检查不一定都要走完,只要有两种方法给出相同的结果,我们就采信这个结果。就像三个朋友一起看电影,只要有两个人觉得好看,那这电影就算推荐了!
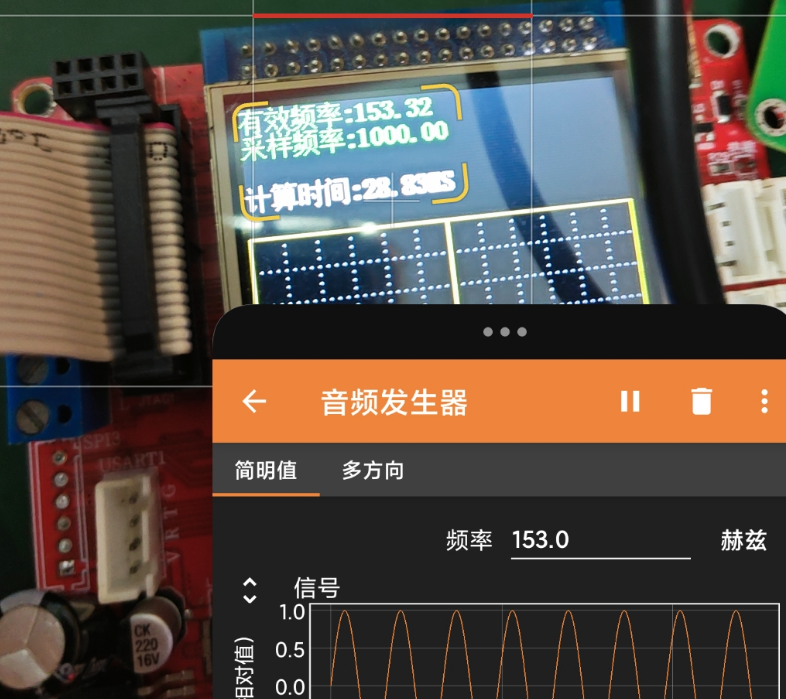
经过前面几个方法的分别实测,这样一整个流程所占用时间是不会超过50ms,具体的计算量需要根据MCU性能以及采集数据量计算,以下是STM32F103的72M采集1024个数据的计算时间(28.83MS)。
5. 决策融合
整个流程是这样的:先用RMS法快速筛选,能量特征明显的波形直接分类;特征不明显的样本再用阈值比较法检查时域分布特征;最后还确定不了的波形,就用频域分析法做判断。这种融合方法比单一方法识别准确率更高,抗噪声能力也不错,资源占用比纯频域方法少很多。不过缺点也很明显:系统复杂了不少,代码维护起来更麻烦;多层决策让响应速度变慢了;而且多个算法的参数协调和校准也更复杂。
可视化理解
为了更直观地理解波形识别的过程,本文特意部署了两个可视化界面,分别是阈值比较法,与频域波形识别法,可视化界面的部署,方便刚接触的这一方面的读者理解。
阈值比较法可视化
点击或者复制到网页进行查看:(如以下链接失效,请联系邮箱:3196685477@qq.com)
阈值比较法链接
源链接: https://ylh513.github.io/ylh_page2.github.io/
加速链接:https://ylh-page2-github-io.pages.dev/
建议开启网络代理访问,如无网络代理,优先选择加速链接,如失效,再访问源链接。
界面展示:

频域波形识别法链接
源链接: https://ylh513.github.io/ylh_page1.github.io/
加速链接:https://ylh-page1-github-io.pages.dev/
建议开启网络代理访问,如无网络代理,优先选择加速链接,如失效,再访问源链接。
界面展示:
边缘AI决策方案
使用以上的纯规则策略,也能实现波形识别这个功能,虽然这几种典型波形识别起来能实现,但是需要添加一种叠加波形或者别的波形时候作为识别目标的时候,这个时候我们又要去分析这个波形的特征,需要从各个角度去分析,然后调节参数、算法策略,才能设计出合适的识别策略,这样整个项目的时间更复杂度比较高。
在这之前我也一直在思考:有没有一种方法?就像可以在Linux上运行yolo一样,提供足够的训练数据,训练好模型,部署在Linux这种轻算力上,就能根据数据标注出目标的类别。
后来我偶然接触到ST的NanoEdge AI,最初用于音频信号检测场景。随后在官网深入了解其功能后发现,它比之前使用的CUBE AI工具链友好得多——Cube AI需要具备人工智能相关知识才能上手,往往需要与AI专业人员合作,因此性价比相对较低。于是我抱着尝试的心态,先通过树莓派脚本完成模型训练验证,随后顺利迁移到目标硬件进行上板实验。
NanoEdge AI
NanoEdge AI是STMicroelectronics推出的一款专为嵌入式系统设计的AI工具链,它允许开发者在资源受限的微控制器上实现机器学习功能,无需深厚的AI专业知识。该工具链的核心优势在于其自动化模型生成流程和轻量化部署能力,特别适合波形识别等实时嵌入式应用场景。
官网:https://stm32ai.st.com/zh/nanoedge-ai/
核心功能特点
- 自动机器学习(AutoML):通过自动特征提取和模型优化,简化AI模型开发流程
- 超低资源占用:生成的模型可在RAM小于10KB、Flash小于100KB的微控制器上运行
- 实时推理能力:针对时间敏感型应用优化,推理延迟可低至微秒级
- 离线学习支持:支持在终端设备上进行增量学习,适应环境变化
- 易上手:只需要简单四部就能添加到项目中
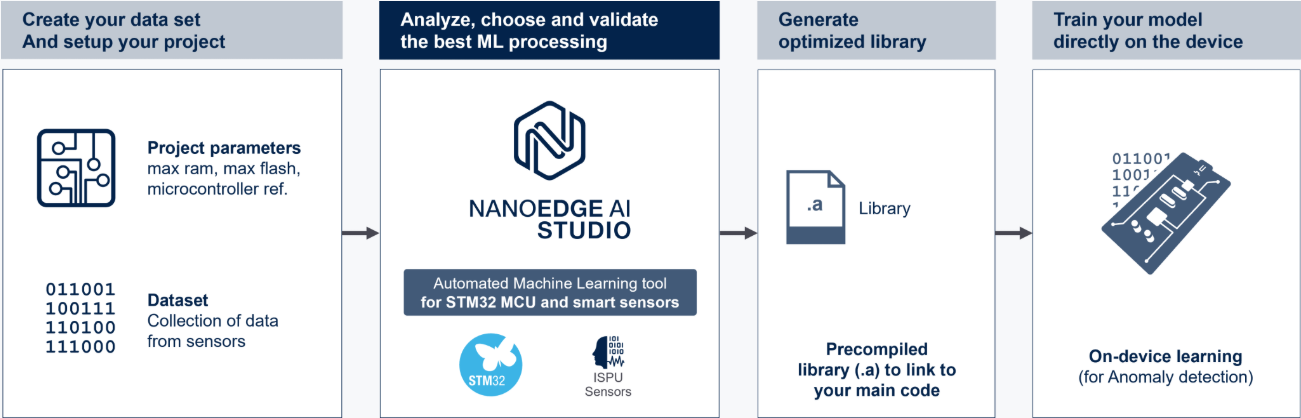
在波形识别应用中,NanoEdge AI可通过以下方式提升系统性能:
- 直接处理原始数据,减少特征工程工作量
- 提供多种波形分类算法模板,包括异常检测和识别
- 内置硬件加速优化,充分利用ARM系列MCU的计算资源,这也包括一些国产的ARM的MCU也能进行使用
具体介绍

上图展示了NanoEdge AI针对波形识别场景提供的四大核心功能模块,每个模块均针对边缘计算环境进行了深度优化:
1. 异常判断
核心能力:模型对正常数据与异常数据进行训练学习后,可识别判断数据是正常还是错误状态
- 与传统阈值判断的优势:当数据多维时,阈值判断难以设定合理边界;而机器学习模型可在MCU端进行数据学习优化,自动适应数据特征变化,避免手动调整阈值的麻烦
- 实现原理:通过设备端持续学习建立正常模式基线,无需大量标注数据即可实现异常检测
- 应用场景:电机振动异常检测、心电信号异常波动识别
2. 单分类
核心能力:将数据导入并进行机器学习后,可判断设备状态是否正常
- 与异常判断的区别:单分类将所有非正常数据统一判断为异常,不提供相似度分析
- 技术特点:单类别训练模式,大幅降低标注成本,特别适用于数据高度不平衡场景
- 应用场景:工业设备状态监测、环境异常检测
3. 多分类
核心能力:对多个状态的数据分析训练后,可输出当前数据对应各个状态的相似度
- 技术特点:支持多类别波形识别,提供混淆矩阵可视化
- 实现优势:内置特征选择算法,自动提取波形关键特征点,优化分类边界
- 应用场景:声纹识别、多类型传感器信号分类、设备多状态监测
4. 推断
核心能力:过往数据进行分析训练,生成的模型可根据近期数据预测下一个时刻可能的数据
- 技术特点:支持线性与非线性波形趋势预测,可配置预测窗口长度,内置预测置信度评估
- 资源优化:平衡预测精度与计算资源占用,适合边缘计算环境
- 应用场景:生理信号趋势预测、振动疲劳寿命预估、设备性能退化预测
具体的内容官方文件里面介绍的很详细,还有各类的示例使用案例,请详细阅读!!!
官方介绍文档:https://wiki.st.com/stm32mcu/wiki/AI:NanoEdge_AI_Studio
方法验证
了解到NanoEdgeAI之后,我在想是否可以用这个模型来实现周期波形识别的项目。首先为了节省开发实际成本,我选择在树莓派上进行模型的训练和验证。
具体的方法步骤如下:
- 准备数据:使用数据脚本进行生成波形数据,PC端只需要打开串口进行接收数据即可。
- 数据预处理:为方便模型进行识别,对数据进行预处理,每个波形的幅值进行归一化,这样给模型训练提供了优质数据进行训练。
- 模型训练:在NanoEdge AI Studio中进行模型的训练,选择单分类模型,将不同的周期波形作为不同的类别,模型会自动学习每个类别的特征表示。
- 模型验证:使用训练好的模型对新采集到的波形数据进行分类识别,评估模型的准确率和召回率。
为了方便模型验证,我使用了PC端的Python脚本进行数据的采集和模型的验证。
为了方便大家进行模型训练学习,本文提供一套调试程序,方便大家进行模型的训练和验证。
项目地址:https://gitee.com/(未构建无效链接后续部署!!!)
具体方法
环境搭建
- 树莓派系统:Raspbian操作系统
- Python环境:使用Anaconda进行Python环境的搭建
- 方式:使用SSH或者命令行操作
此处重在验证,不会过多赘述相关Linux,如感兴趣请参考网络相关文档以及博客。
1. 树莓派连接网络
- 首先需要打开树莓派的SSH功能,这样才能使用SSH协议连接树莓派。
- 然后需要获取树莓派的IP地址,一般情况下可以在路由器的管理页面中查看。
2. 树莓派使用虚拟环境
- 使用指令安装Anaconda
pip install anaconda - 安装好之后,在文件中找到ylh_env启用虚拟环境
- 激活虚拟环境
source ylh_env/bin/activate
3. 具体操作
在当前目录下

激活虚拟环境

运行脚本

如缺少环境依赖可以上网搜索添加。之后将目标转到PC端,使用运行PC端的脚本,打开PC_Main.py运行程序,选择文件下.ven文件作为虚拟环境,这里的本机IP跟端口号就是需要填写到上图之中的。
接着将图中的本机IP以及端口号填入树莓派中。
接着再次回到PC端,能看到我这里会有两个端口,你们的电脑上是不会显示这两个端口,这个是因为我使用了虚拟端口,具体的如何操作网上有很多教程以及软件工具,这边不多赘述,关键词:虚拟串口、虚拟串口工具。

之后我们随便选择一个串口,这个会把串口一的数据发向串口二,之后PC端会运行一个波形图可视化程序。

此时这个波形图可视化中是没有波形图的,此时回到树莓派中进行波形选择。根据脚本提示进行选择,选择波形数据、归一化(此处的归一化是对幅值进行归一化,不管波形的原始幅值是多少,都将限制在0-1之间,这样的好处就是提高数据的质量,方便数据减少训练,无需考虑幅值带来的影响)、频率、幅值、纹波(模拟实际采集的波形增强可信度)。
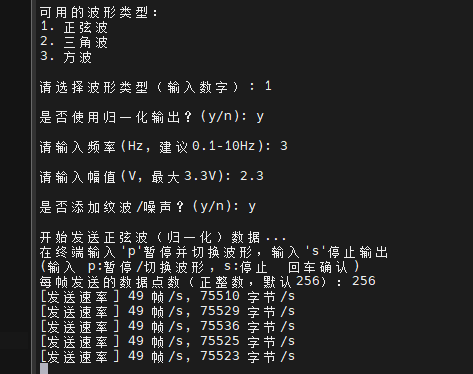
图中是已经开始波形的传输,接着可以在PC端进行查看波形数据。
正弦波可视化。

可调节对称性三角波可视化。
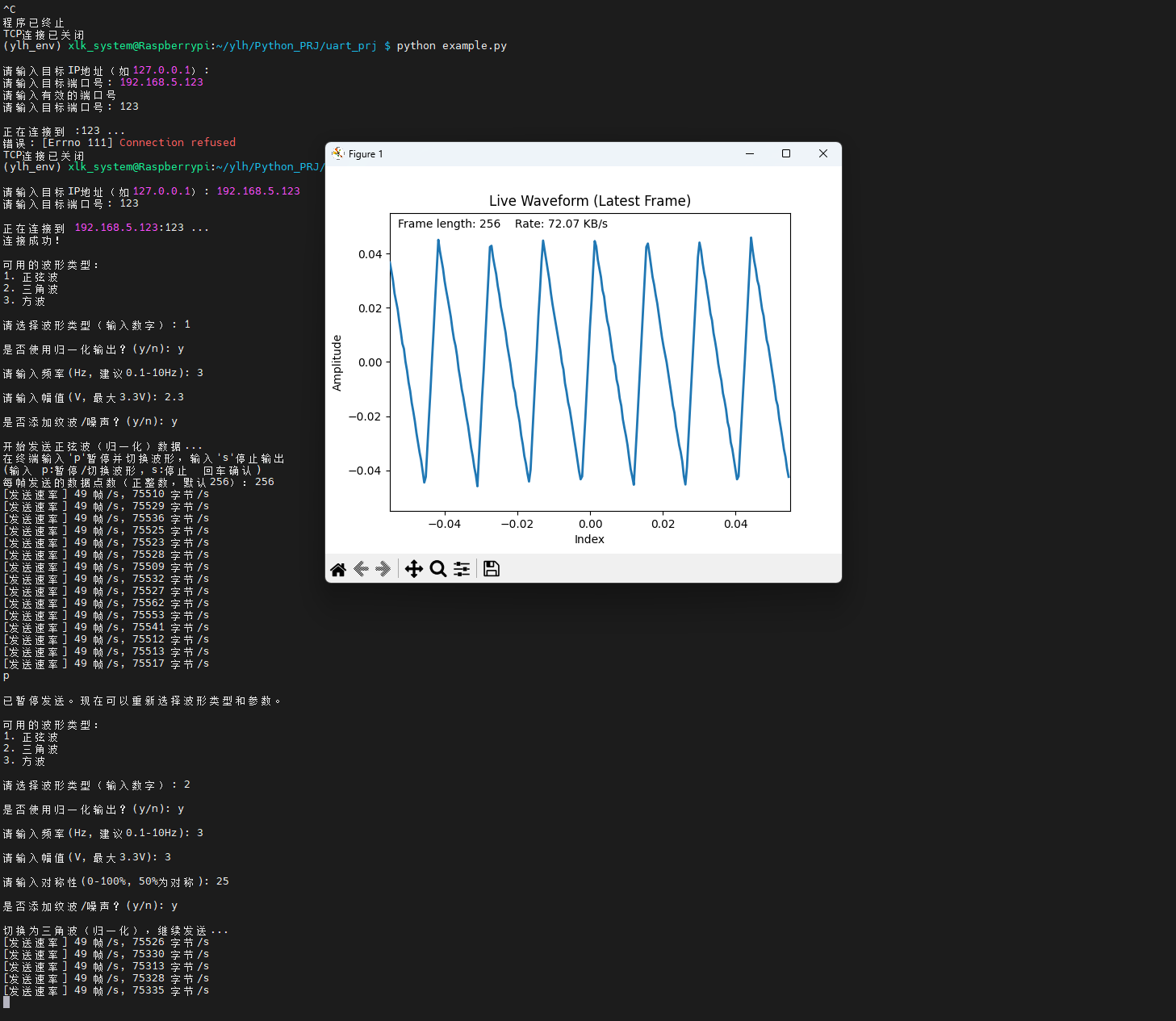
带纹波的方波可视化。
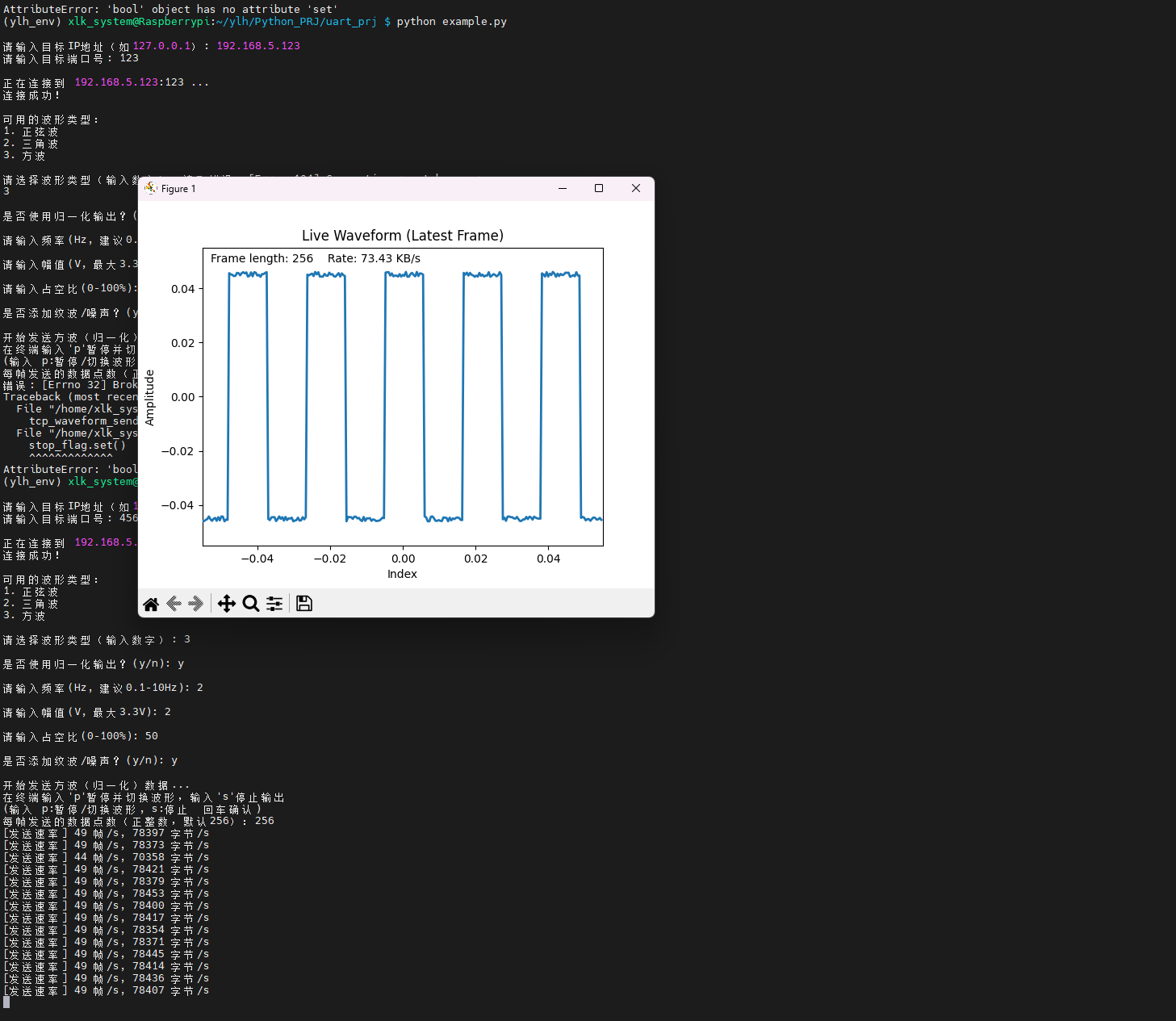
按 P +回车 ,暂停可以对其他波形进行查看。此时观察波形数据是比较符合实际采集波形数据。使用这个目的是能快速验证这个方案时候能正常运行,仓库中还有别的论证脚本,可以使用串口通讯进行波形数据的传输,需要使用TTL串口模块进行通讯,此脚本是无需而外的硬件接线,只需要在同一网络下即可,仓库中还有一键生成数据集的功能等其他开发调试功能,具体的功能请往代码仓库查看!!!
打开NanoEdge AI Studio 创建工程。

具体设置如图。

点击左下角的保存,进入到第二个步骤。
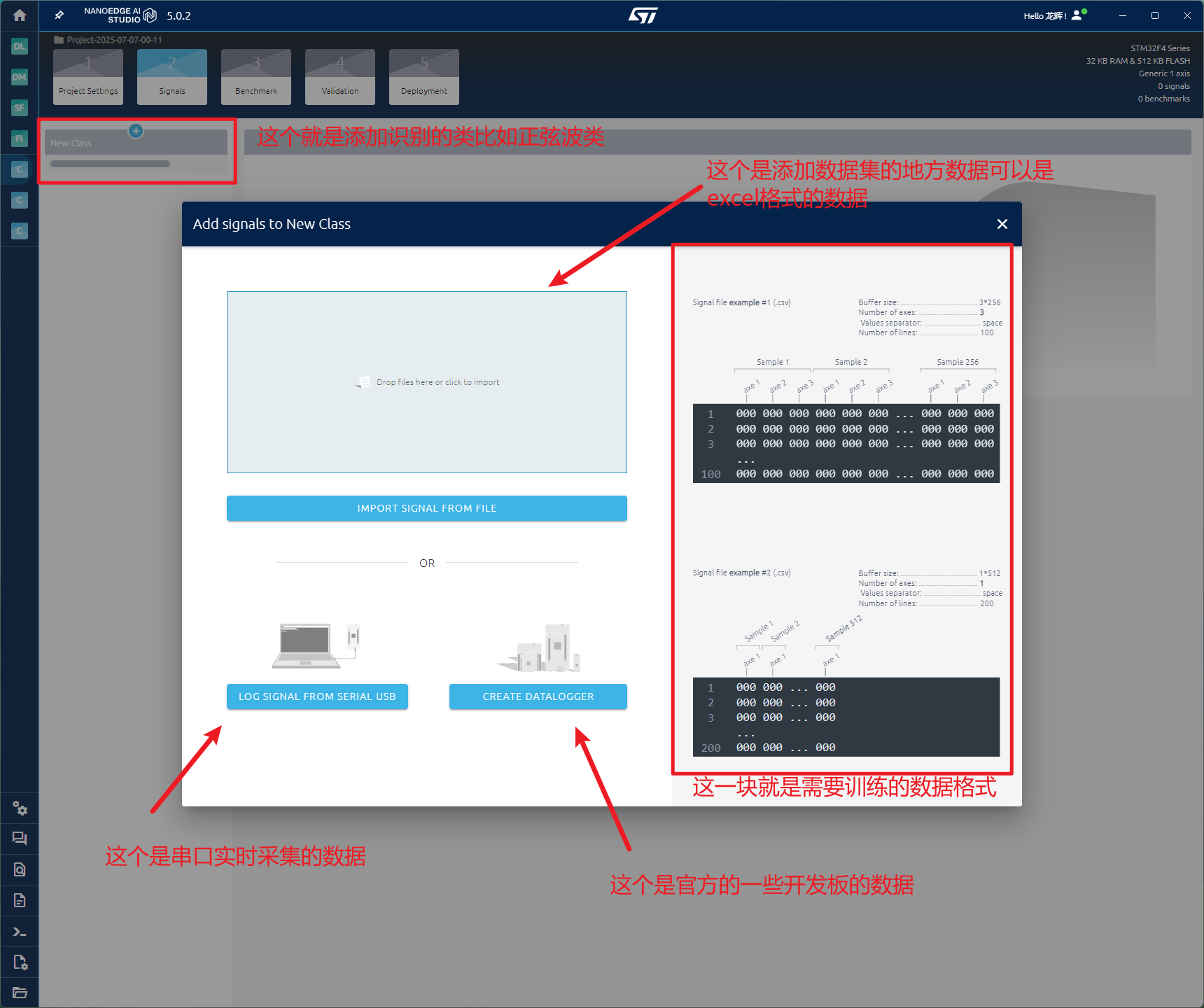
我这边采用的数据集,是之前脚本生成的数据,具体的数据集生成脚本在代码仓库里面,这个是使用脚本生成的数据,这个只是做验证来使用,实际的应用数据还是需要采集板子上的数据,这个脚本数据也可以用来加强模型的识别能力。可以看到图中的数据会进行FFT的预览、数据预览,我这个只是使用256个数据长度,实际的训练数据长度可以根据你MCU采集的ADC缓冲区来定,比如你使用的1024的缓冲区,可以把实际的波形数据通过串口传入进来。我这个是先对正弦波三角波方波进行训练的。使用这个方法的好处就是,你可以随意添加你想识别的周期波形类型,相对于纯规则策略,这个时间上以及复杂度减少了很多。
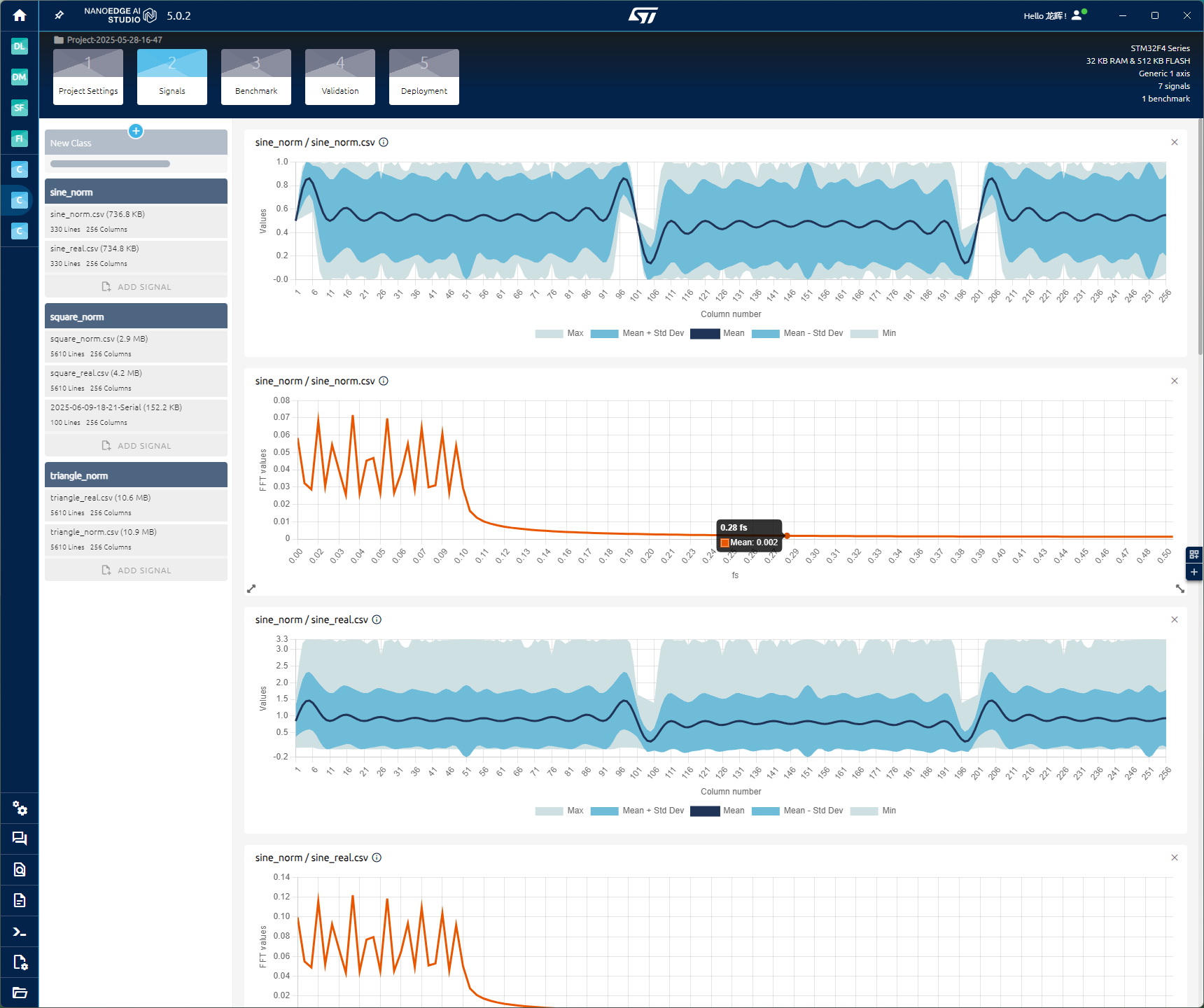
标注主要的板块进行说明。
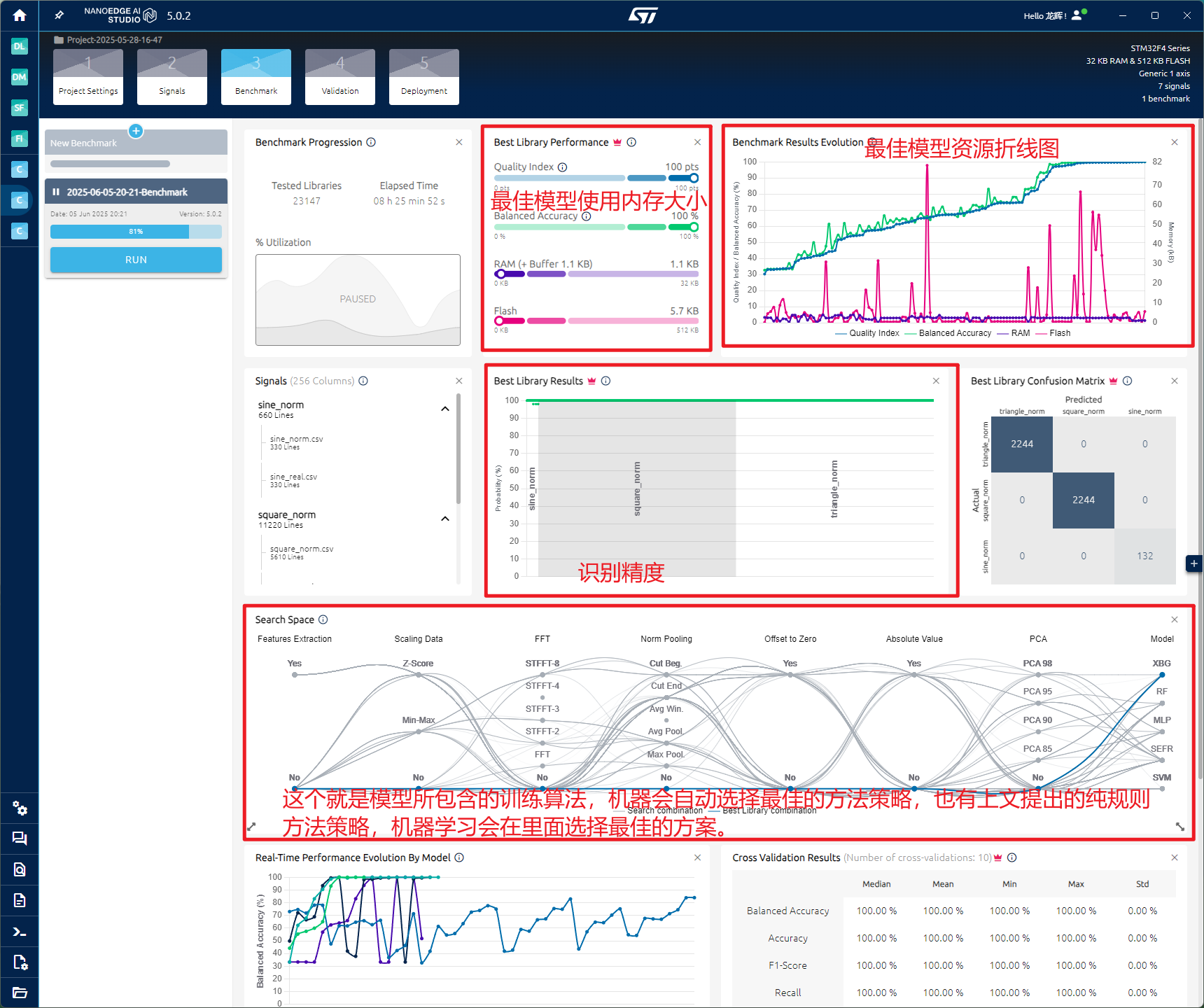
我这边选择暂停训练,因为训练数据需要比较久的时间,点击下一步的选择模型,这里也标注了最佳模型,但是事实还需要自己手动选择合适的模型,这个只是针对于训练集的数据,实际的效果还是要根据模型的方法来的。

这个是最佳模型训练的数据,其实实际上会有点跳动,不够理想。
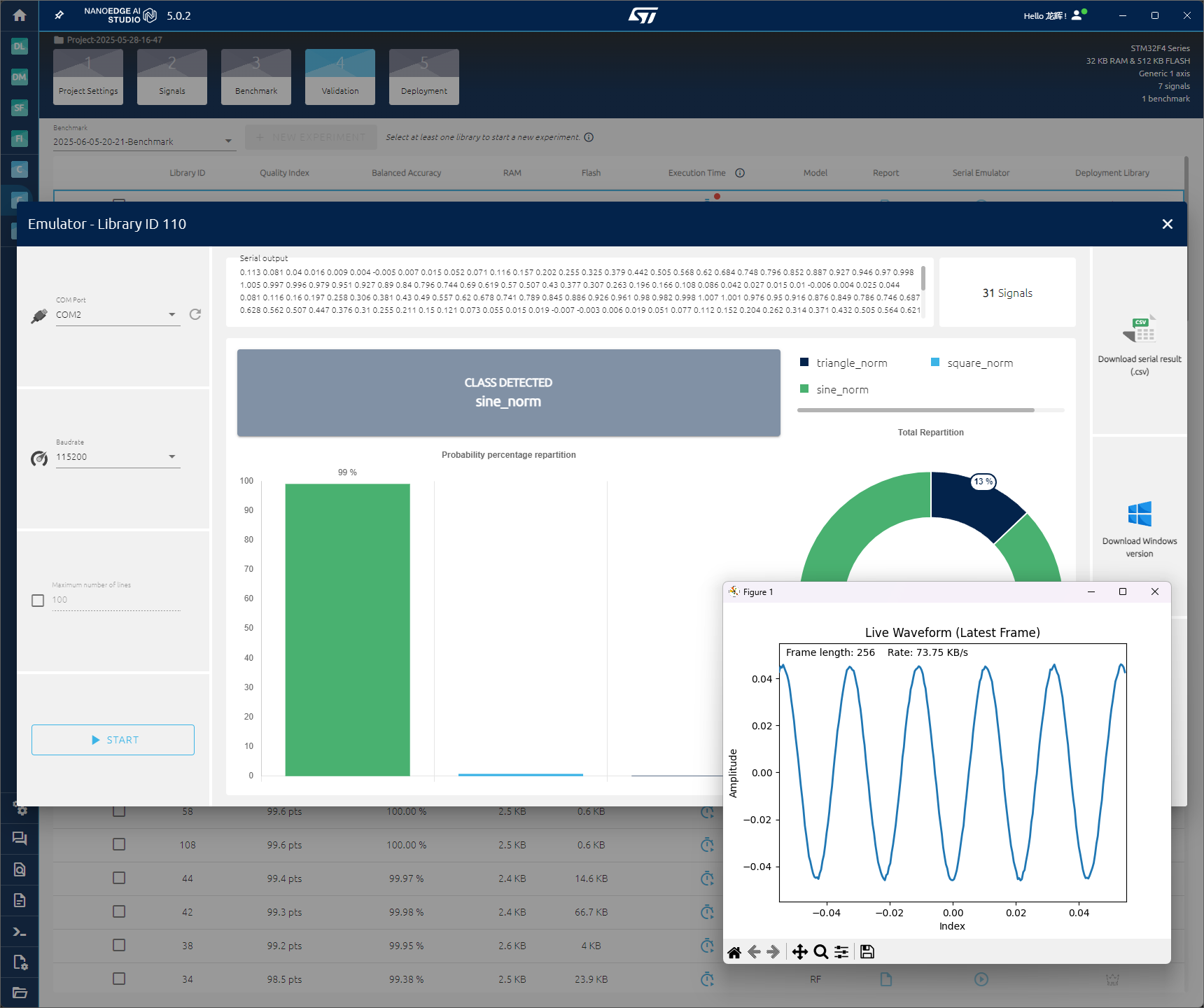
这个是另外一个模型,序号低一点的模型,采集101次,准确率100%。
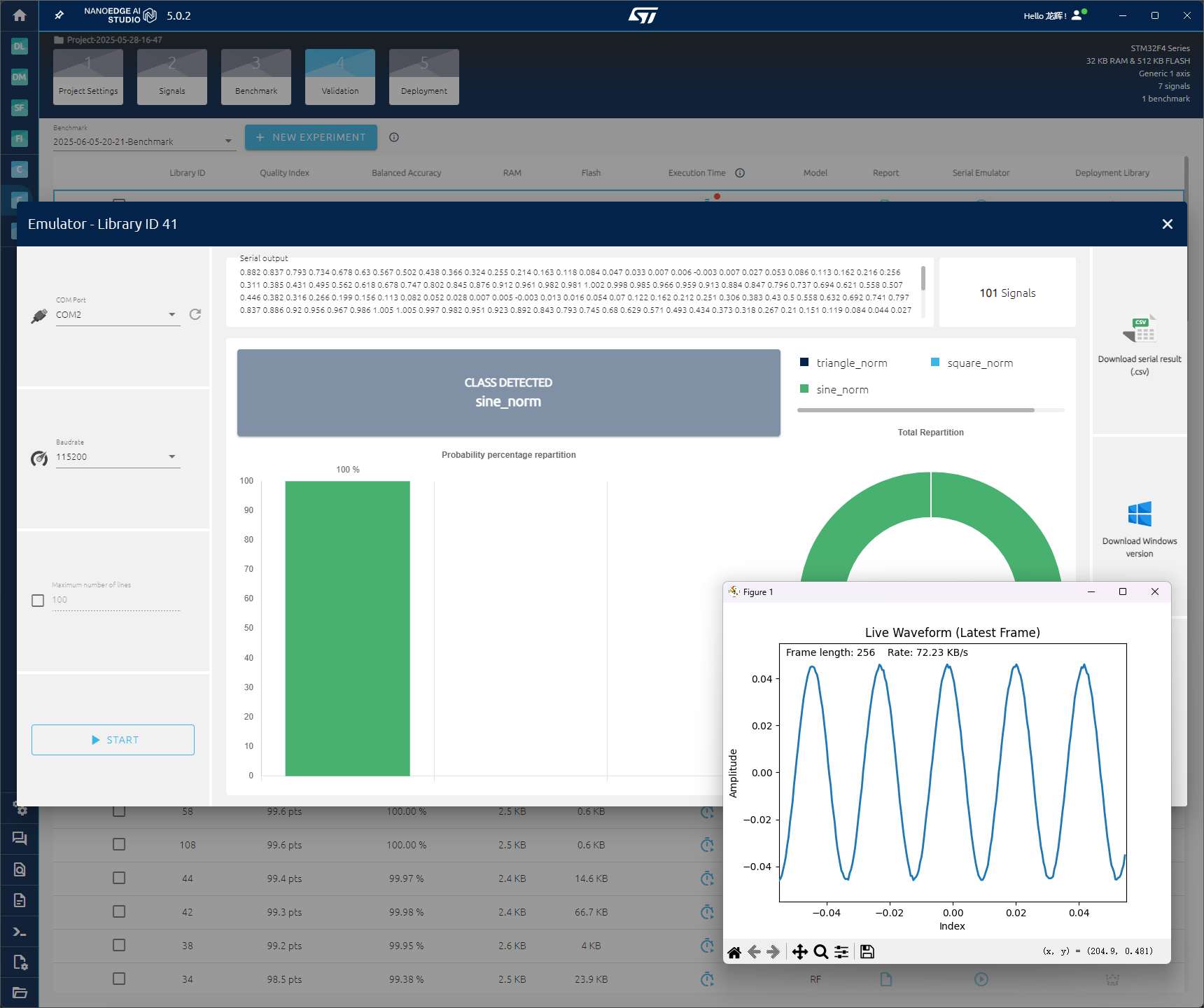
使用三角波采集识别100次,准确率100%
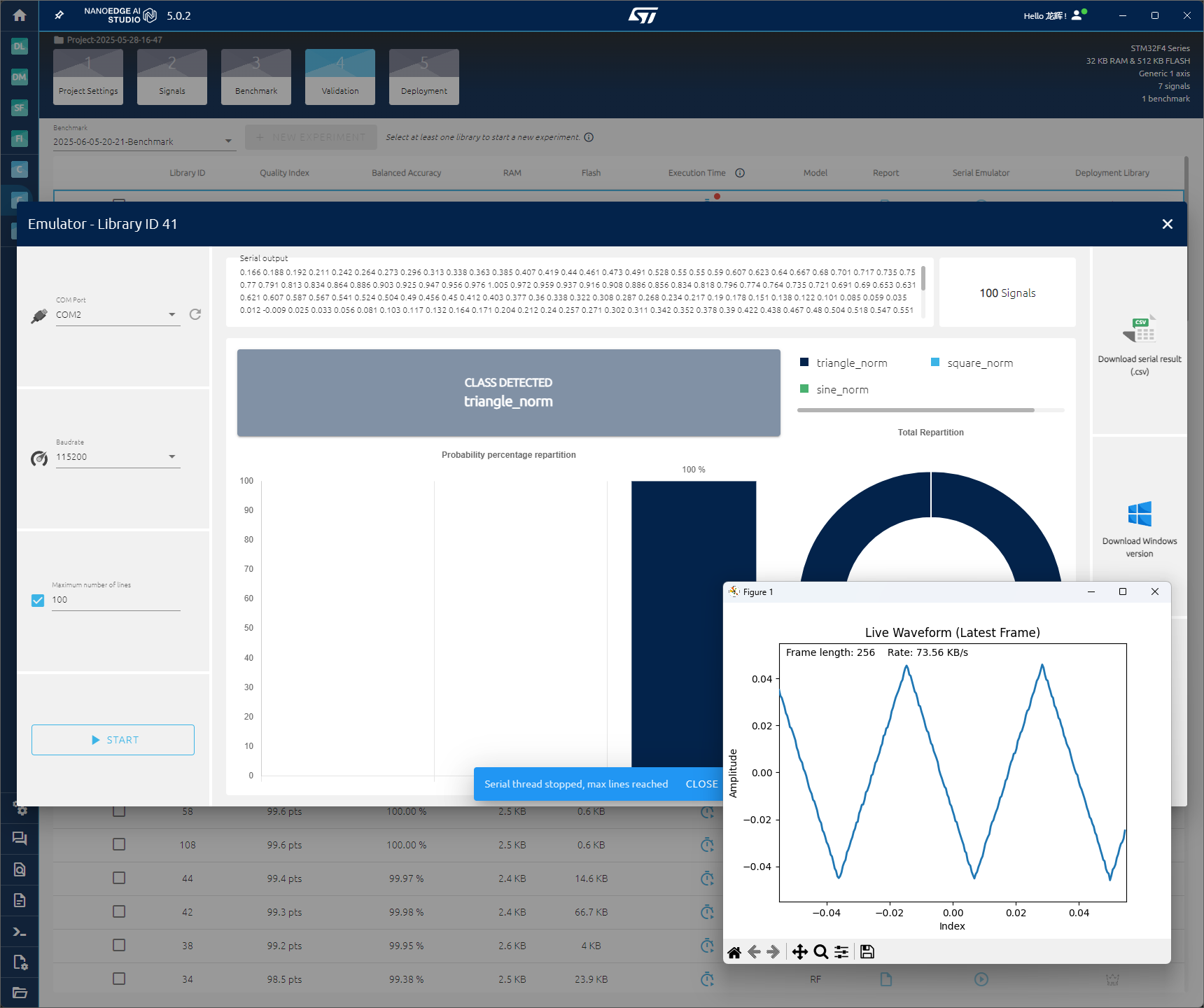
使用方波采集识别100次,准确率100%
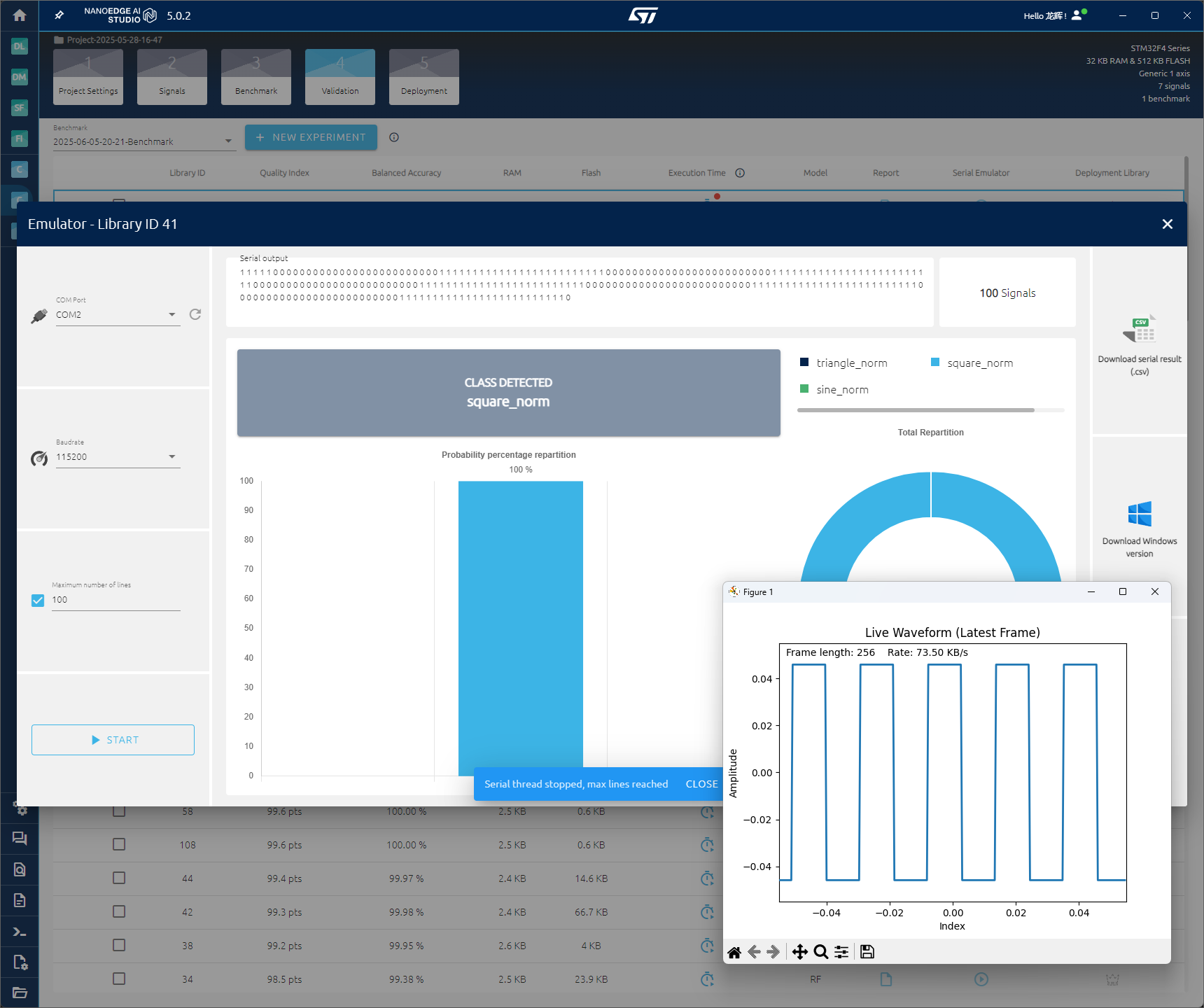
上板验证
经过验证,模型在实际的板子上运行是比较正常的,但是准确率会有一些浮动,这个浮动的原因是因为我这个是使用的是模拟数据,实际的应用数据是需要采集板子上的数据,这个数据是会有一些浮动的,准确率会有一些浮动。
所以为了模型的质量,需要使用实际的板子上的数据进行训练,这样的准确率会比较高。
由于博主目前编写期间,身边没有函数发送器,此期间采用DAC输出的方式来进行验证,DAC输出3种波形,分别是正弦波、三角波、方波,这里以这个三个为典型的代表,实际可以训练任意的周期波形,这边只是为了验证模型的效果,实践中需要训练周期波形根据实际波形进行训练。接着利用串口将波形数据发送到NanoEdge AI Studio进行训练,然后将模型导入到STM32F407VET6上进行验证。
实验环境
软件环境:
- STM32CubeIDE
- STM32CubeMX
- NanoEdge AI Studio
开发板:天空星STM32F407VET6
编译工具链:GCC
注意:此处采用STM32CubeIDE是为了使用GCC编译工具链,因为需要使用到浮点数运行,使用Keil的ARM他们编译器进行编译,这个存在BUG,官方论坛上有详细说明。如果用不习惯这个软件可以选择不使用浮点数进行运算,接着可以使用keil进行编译。
实验步骤
生成波形数据
首先利用DAC生成波形具体的教程可以参考:
【22_2_DAC,DAC+DMA – 实现正弦、方波、三角信号输出, STM32CubeMX应用】https://www.bilibili.com/video/BV1nX4y1Y7e1?vd_source=64a20582db20b4ff6e1c476dceaf13aa
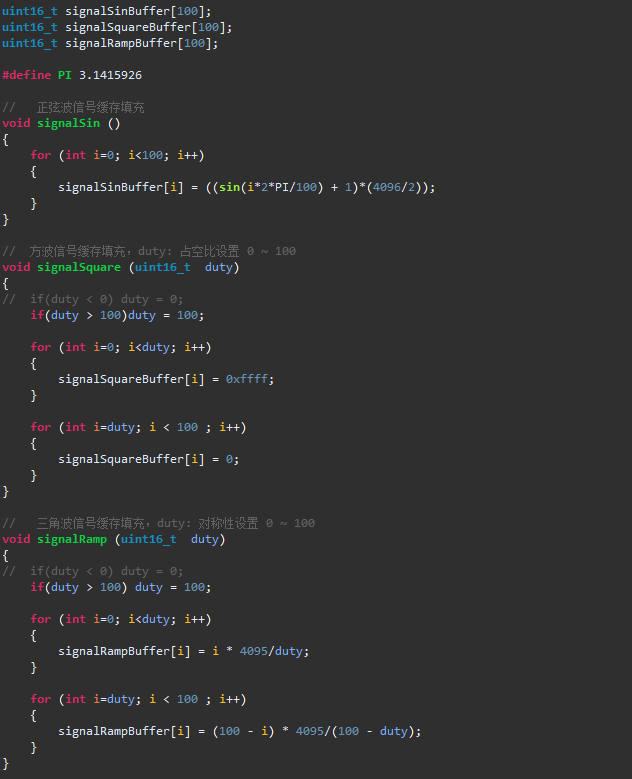
注:此代码来自【22_2_DAC,DAC+DMA – 实现正弦、方波、三角信号输出, STM32CubeMX应用】https://www.bilibili.com/video/BV1nX4y1Y7e1?vd_source=64a20582db20b4ff6e1c476dceaf13aa
具体的波形生成的细节请查看以上视频链接
波形数据串口输出
将生成的波形数据通过串口输出,利用串口训练数据。
需要将DAC与ADC的IO进行短接,这样ADC就可以采集到DAC生成周期波形数据。如果有函数发生器可以直接就使用函数发送的数据进行训练。

首先我们要利用NanoEdge AI Studio的串口作为训练进行简单模型训练,就需要查看它的串口作为数据传输的传输格式。

通过以上的格式,编写打印函数,使用的缓冲区大小是256。
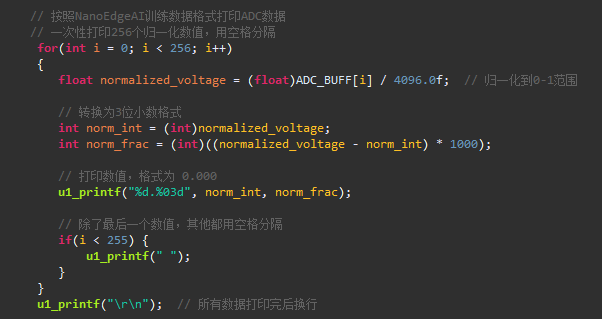
训练数据我以三角波为例。

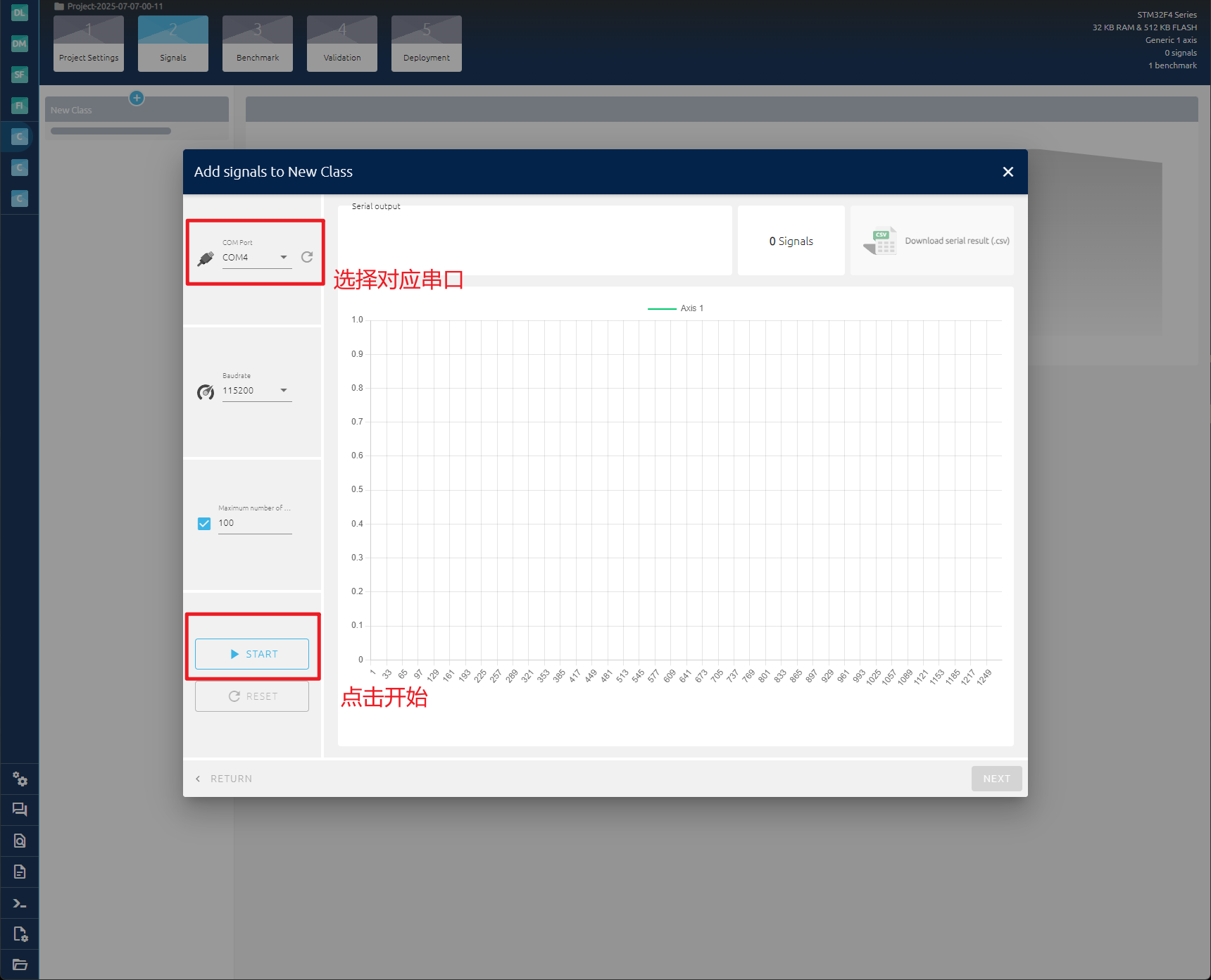
接着打开NanoEdgeAI Studio,点击使用串口数据进行训练。

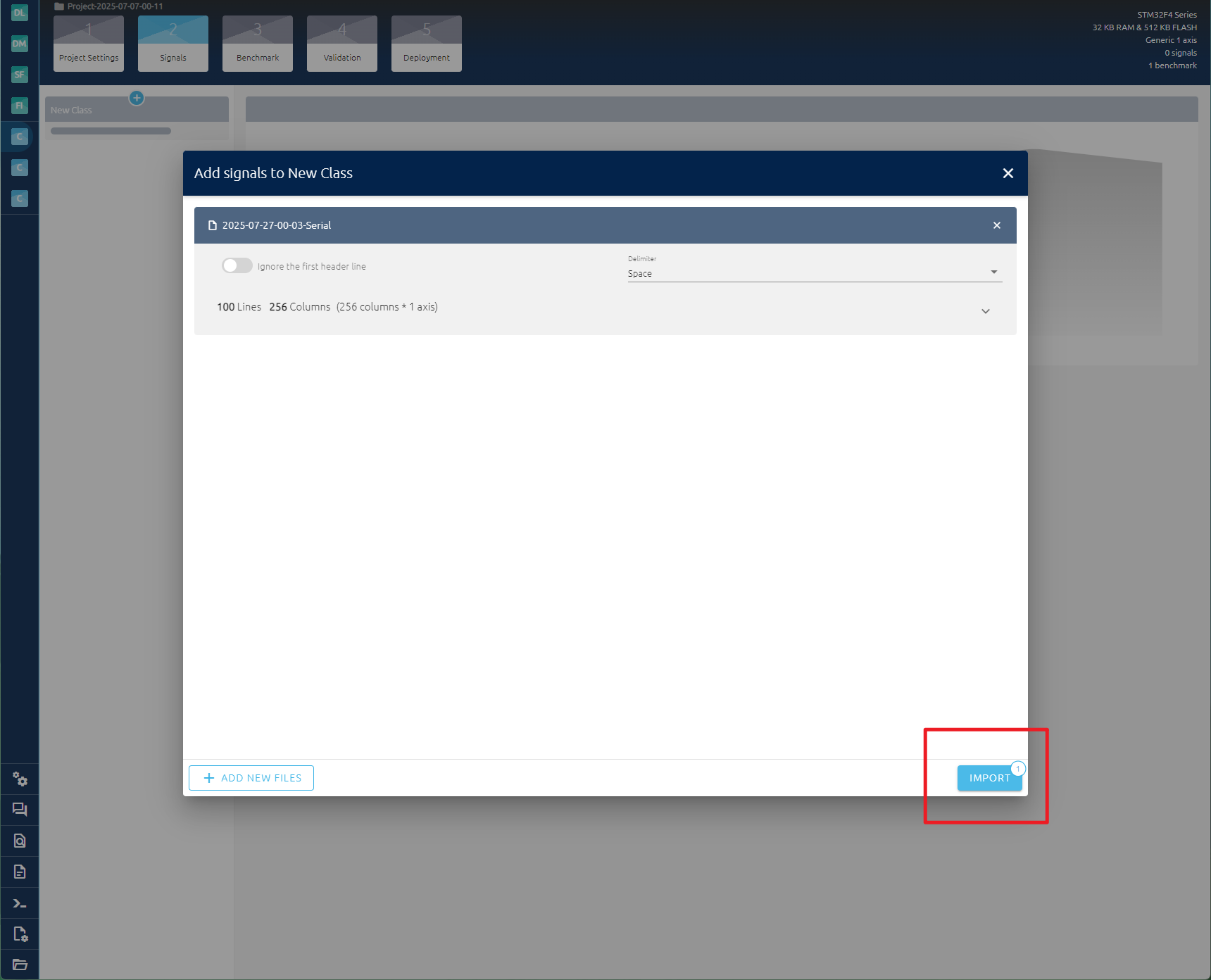
训练好这个波形的数据集就点击下一步。

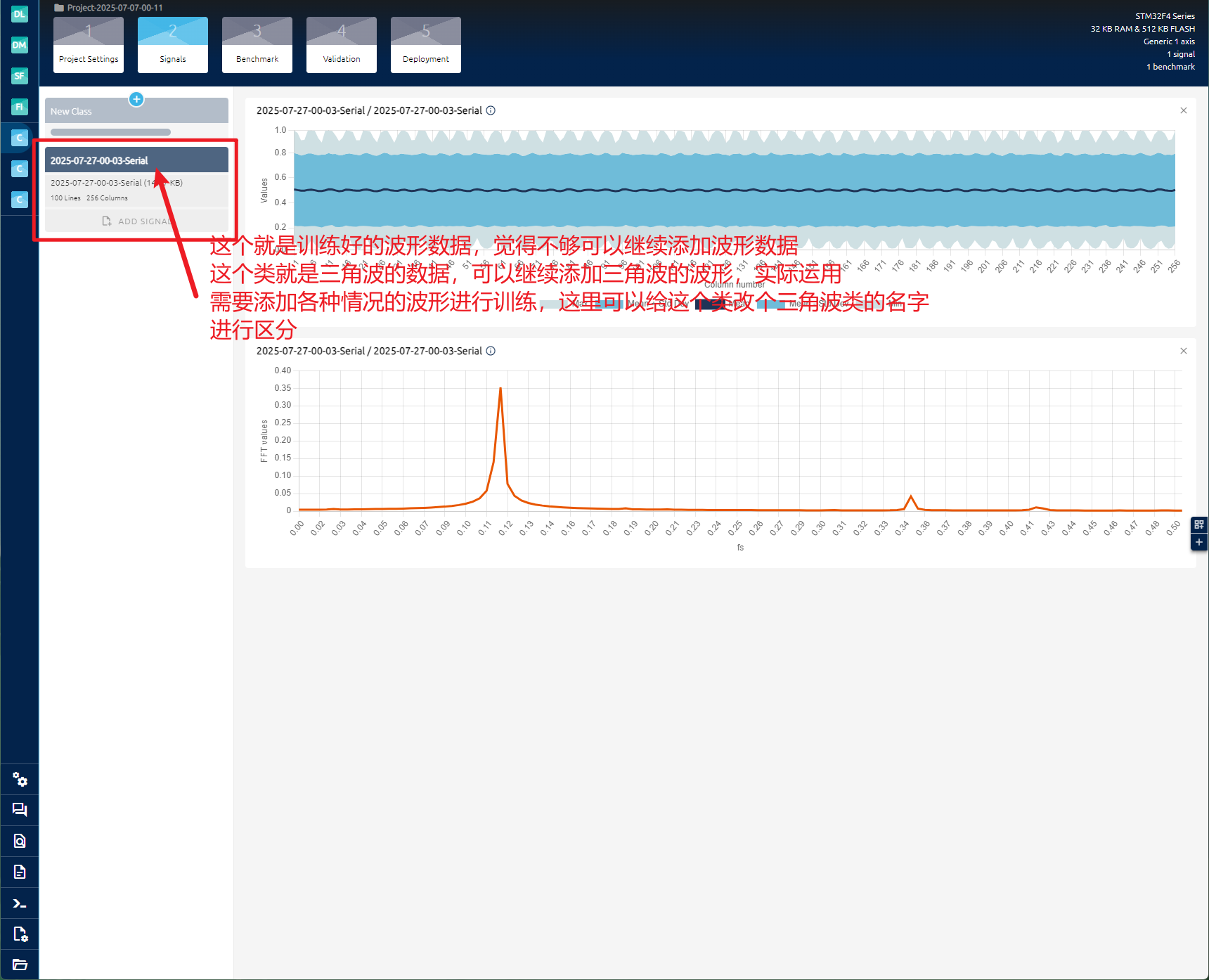
到这里,已经有了三角波的的数据集了,按照这个步骤继续采集正弦波以及方波的数据,如果你们有函数发生器可以使用函数发生器进行实际的数据采集,然后进行数据集的整合,没有的话可以使用教程里面的DAC方法进行生成数据,再由单片机ADC进行采集。
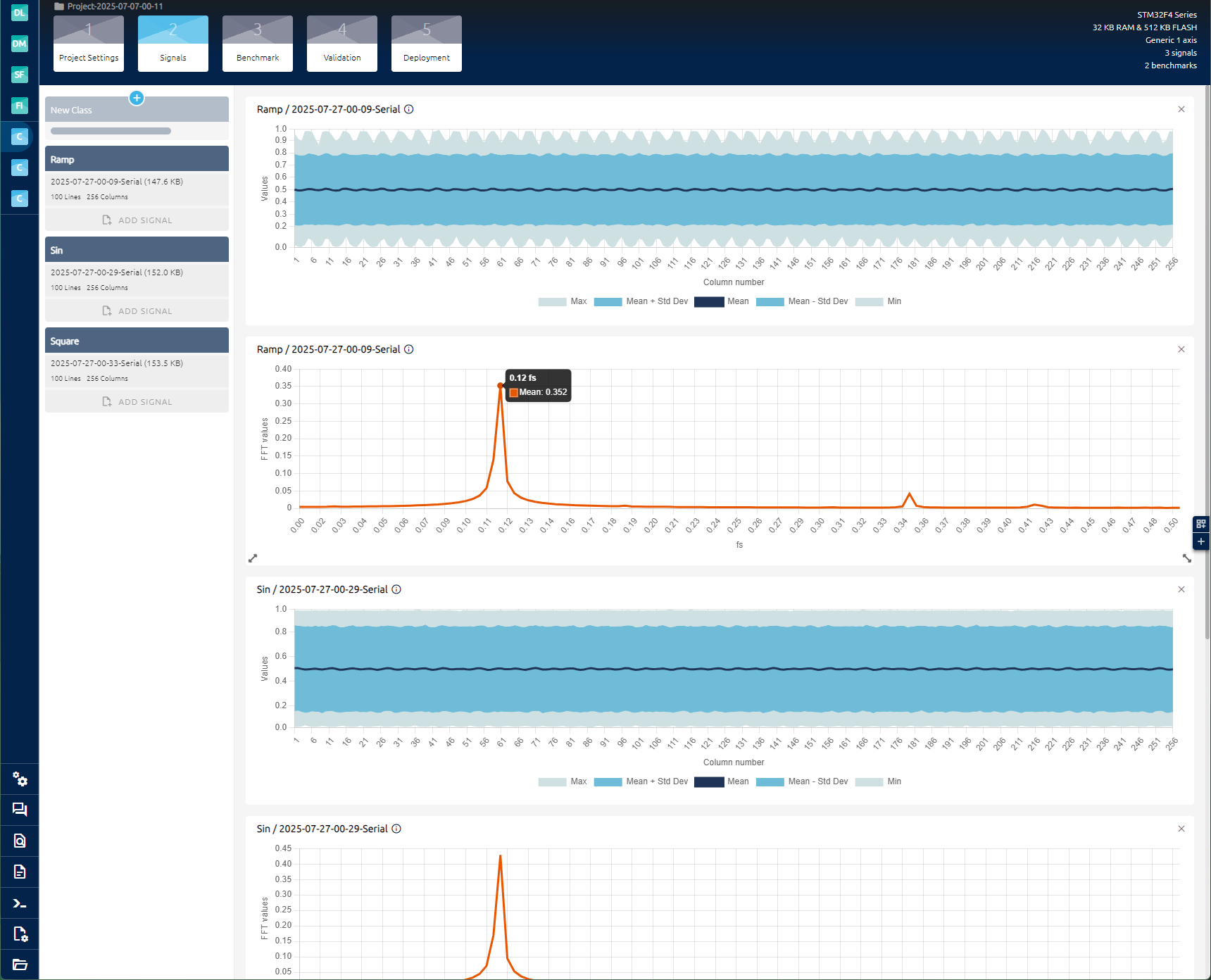
选中数据集进行训练
这里可以等待模型训练完毕,也可以去下一步选择以及训练好的模型,模型训练时间根据你的电脑配置以及数据量的大小直接影响的。一般最好是等待这个训练数据全部跑完,再去选择模型,这样的模型质量会好一点。

根据实际选择最佳的模型。

点击部署模型。
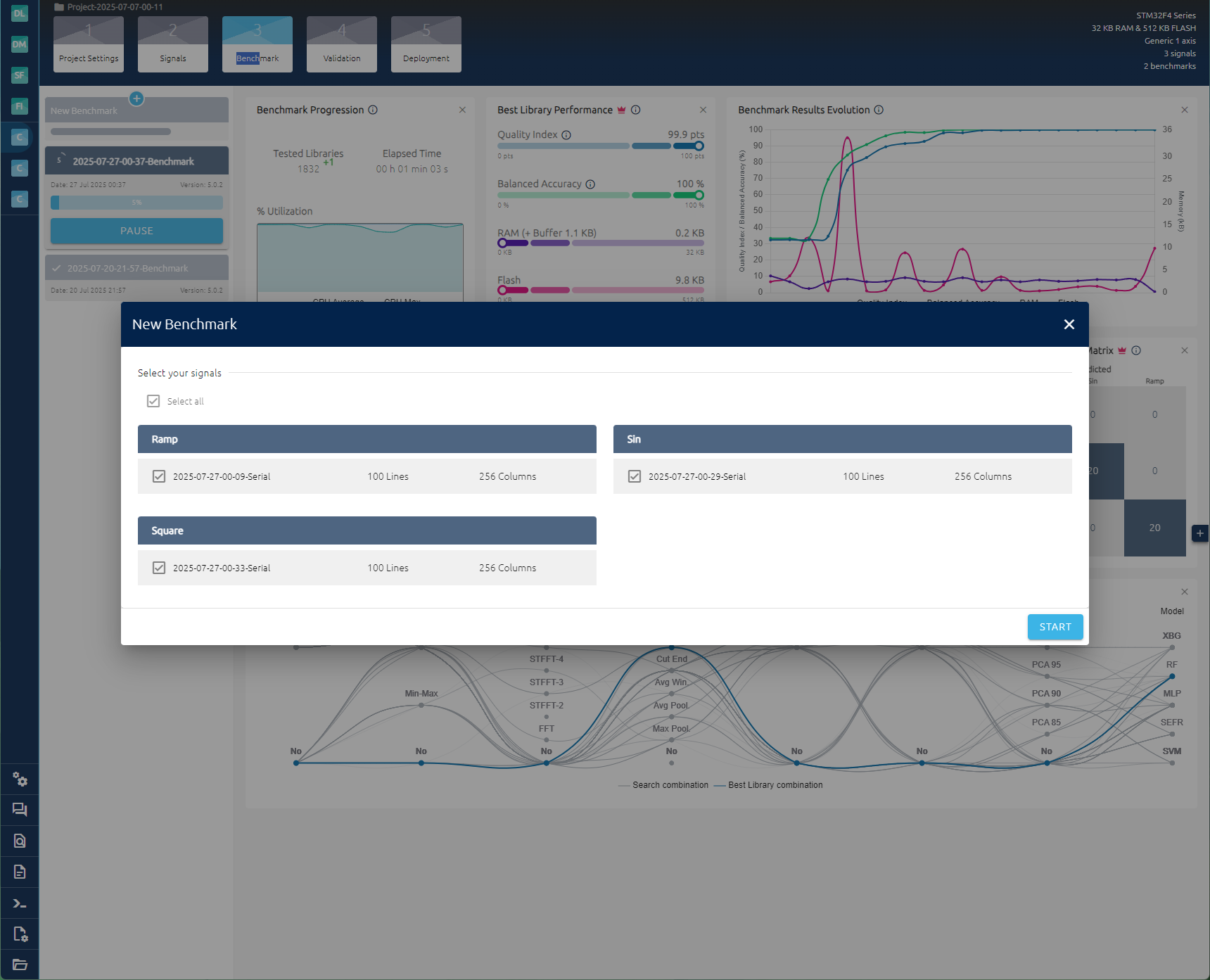
 将模型保存下来,之后打开文件夹。
将模型保存下来,之后打开文件夹。
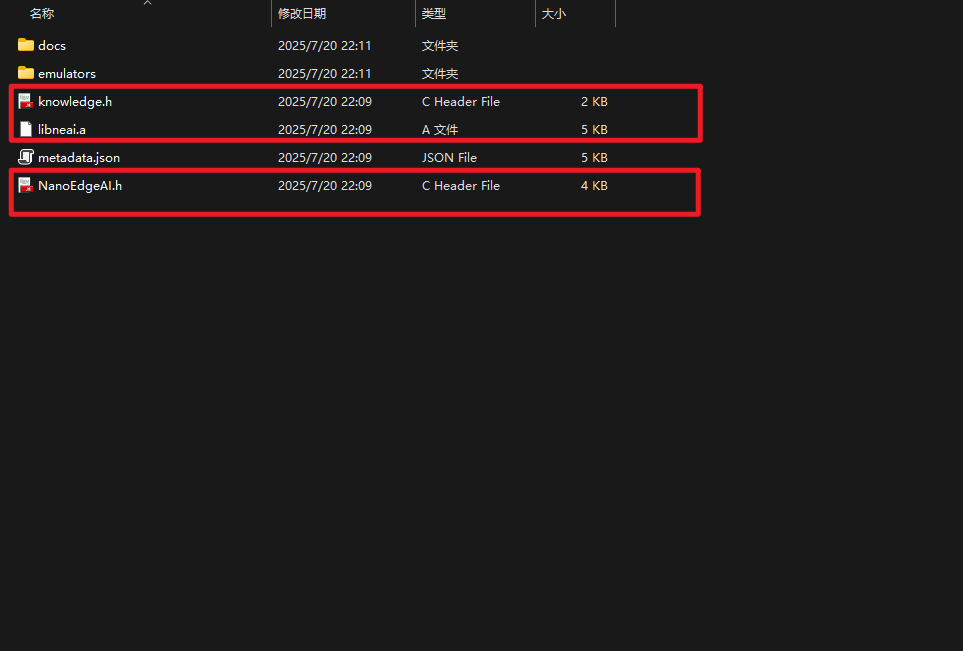
复制所选的文件到工程之中。并且添加到工程之中,以下是.a文件的方式,剩下的自行查阅网上资料添加.c与.h文件。
接着复制图中的示例,根据所在位置进行添加到工程之中。
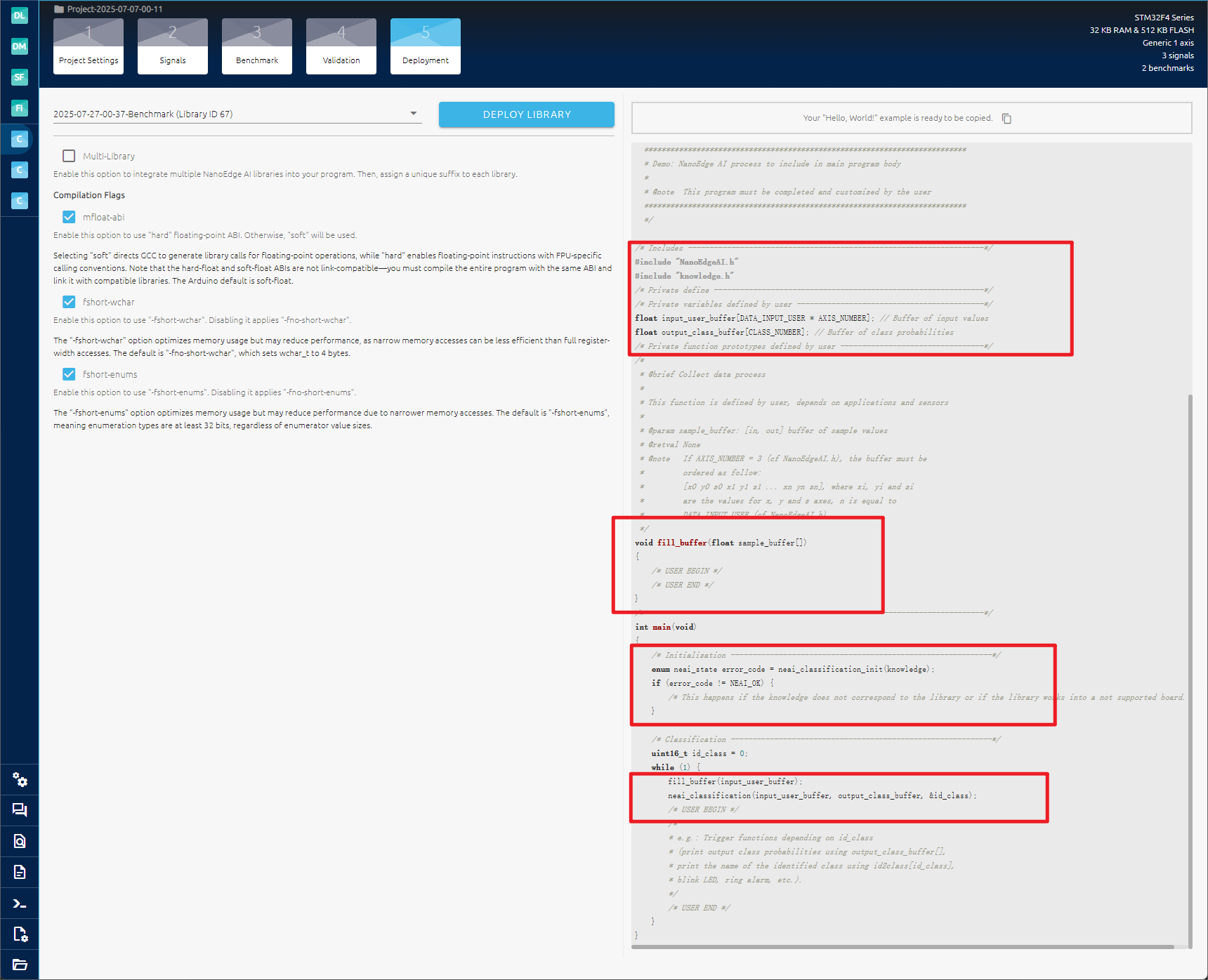
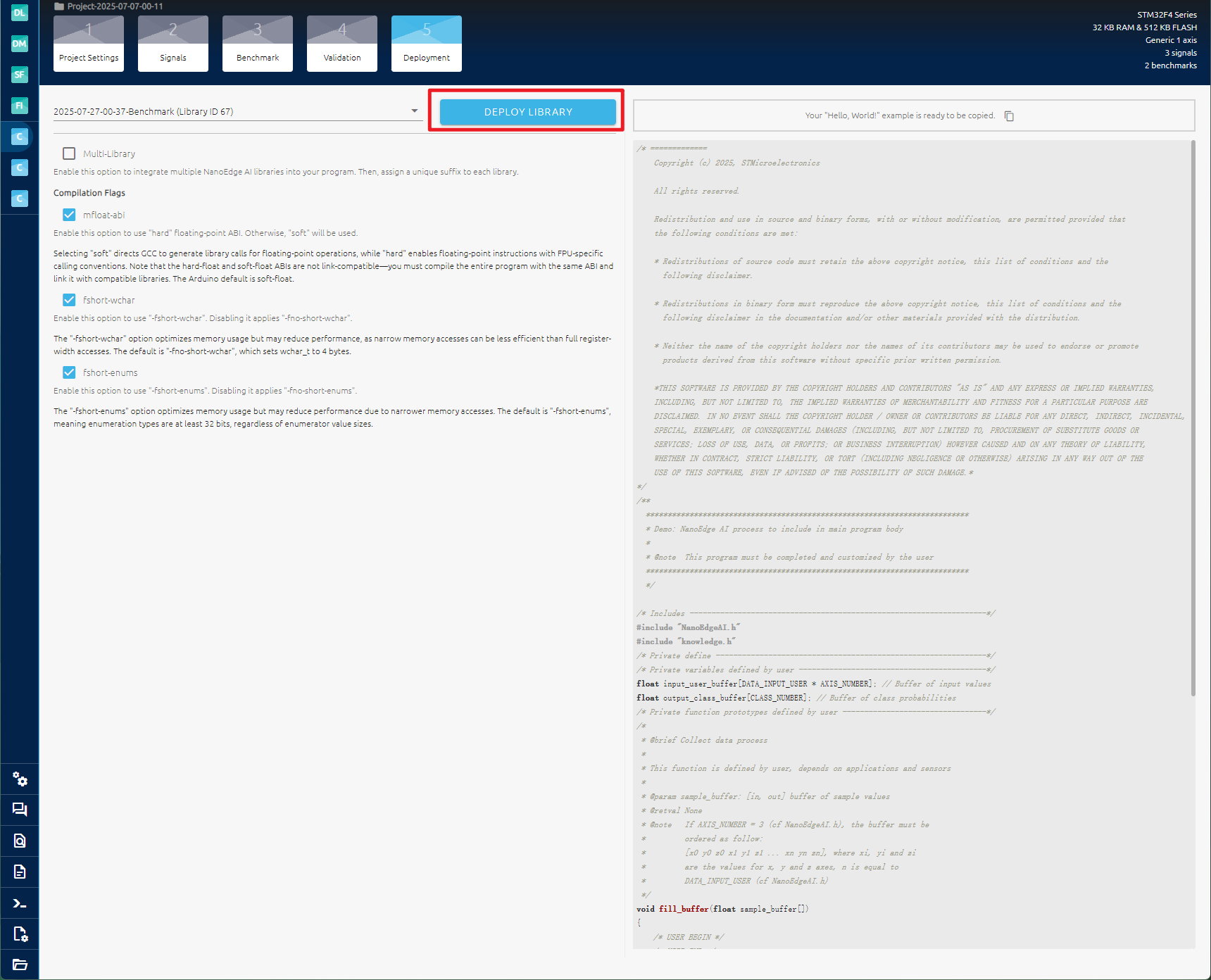
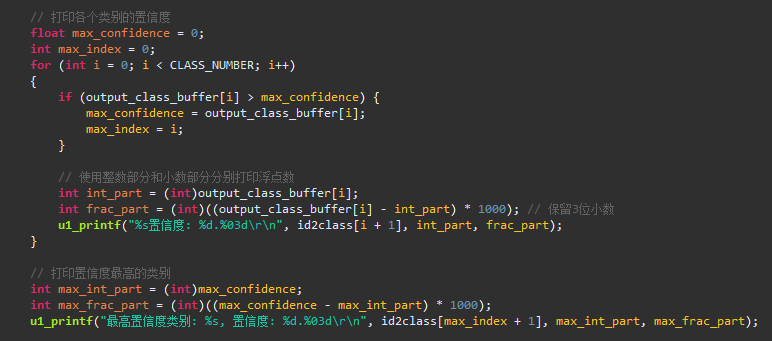
最后添加串口数据输出。
接着打开串口助手查看,识别是否准确。
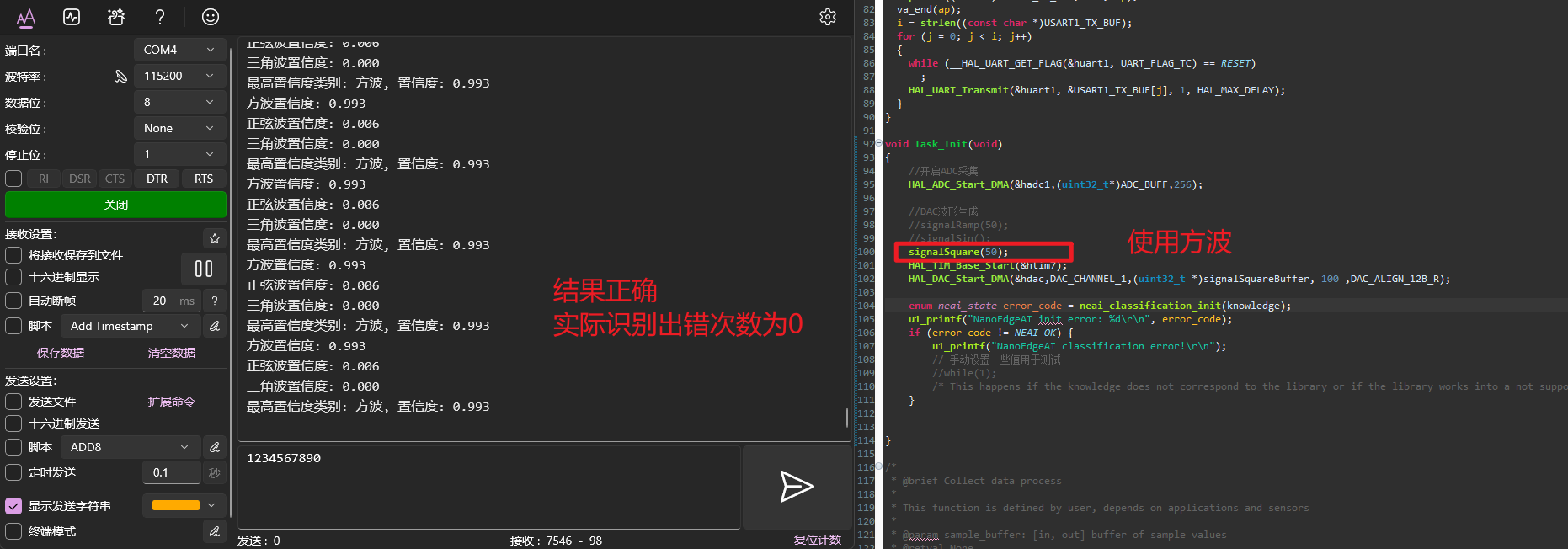
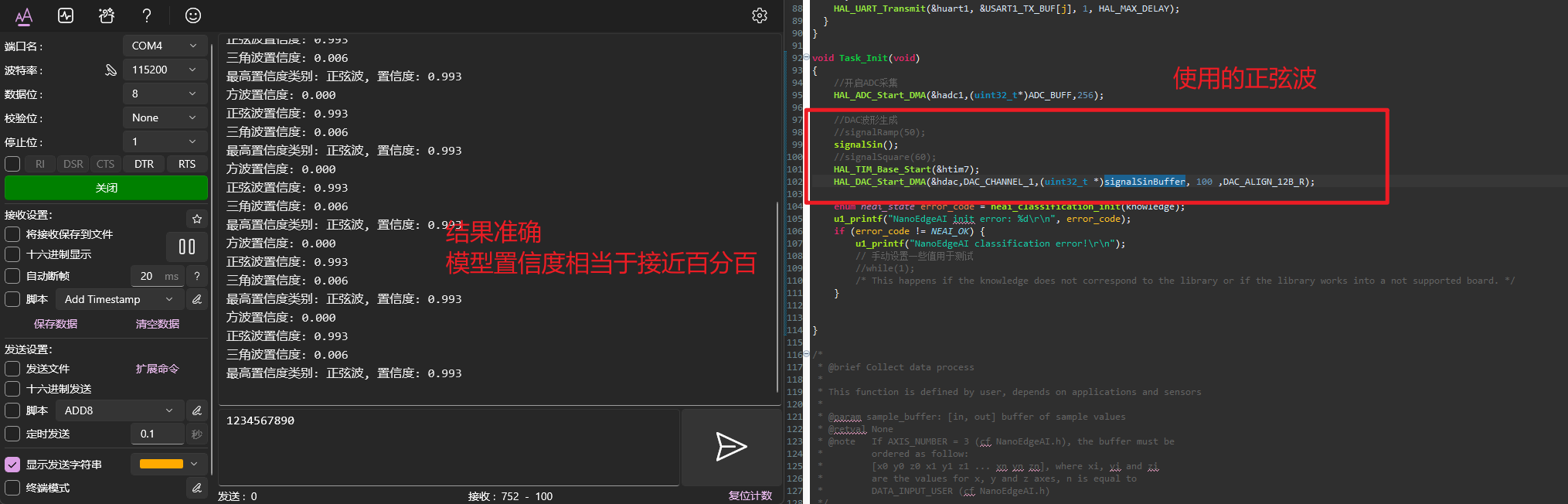

至此,上板验证成功。
需要注意的是,不同频率的波形以及各种实际应用中可能遇到的问题(如噪声干扰、波形畸变等),都需要通过相应情况的数据进行训练学习,这样才能构建出一个鲁棒性强、适应性广的波形识别模型。我这样少量数据做是为了展示整个开发流程。
总结
总的来说,把传统的规则决策方案和边缘AI模型方案放在一起比较,能明显看出后者在波形识别任务中的优势:
- 开发效率高:用边缘AI模型来搞波形识别,流程简单多了。特别是当你想添加新的波形类型时,不用再去费劲地分析特征和调算法参数,省了不少事。
- 识别准确率高:机器学习模型能自动提取特征,区分不同波形更准确,尤其是在处理复杂或相似波形时,效果比传统方法好不少。
- 适应性强:边缘AI模型支持增量学习和在线优化,能根据环境变化和新场景自动调整,用起来更灵活。
虽然边缘AI方案对计算资源和模型训练还有一定要求,但综合来看,它在提高识别准确率和简化开发流程方面的优势很明显,是周期波形识别的理想选择。随着边缘计算技术越来越成熟,像NanoEdge AI这样的工具链在嵌入式AI应用中肯定会越来越重要。
最后整个代码上传到github上,方便大家下载使用。






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








