蓝桥杯填空题汇总_2024蓝桥杯pythona组-CSDN博客

本文链接：https://blog.csdn.net/weixin_74850661/article/details/145468988

文章目录

确定边界
- 拼正方形
打表巧妙找规律
- 召唤数学精灵
- 斐波那契与7
进制转换
- 穿越时空之门
取模问题
- 数字串个数

法无定法，在于因时因势
难如填空题，也有巧妙的方法去暴力与枚举

喜欢考察的知识点：

动态规划，找规律，数论，日期，进制转换等

确定边界

确定边界，巧妙判断

输出一部分，找规律

拼正方形

在这里插入图片描述

思路分析：由于2*2和1*1的正方形的数量都很多，所以不可能一个个枚举进行判断，那么我们可以思考如果全部的正方形都组合在一起，能够拼接的理论的最大的边长是多少？我们从这个最大的理论边长逐步往小判断
这里我们应该注意到，如果边长是奇数的话，说明最外面的半圈是由1*1的正方形所包围的，如果是偶数，那么就可以先判断2*2是否够，如果不够，再用1*1补上

如果a为奇数，那么所需的1*1的块数就是2*a-1

在这里插入图片描述

import math
a = 7385137888721
b = 10470245

# 理论上的最大值
maxq = math.sqrt(4*a+b)
# 通过计算发现 maxq = 5435123.0
# 发现是奇数，那么就判断1*1的模块是否能够包围半圈
# 需要的数量是 2*（maxq-1）+1
need1 = 2*(maxq-1)+1
print(need1)
# need1 = 10870245.0
# 发现 need > b ,所以这个maxq不满足，那么我们就判断maxq-1的情况
maxq = maxq-1 # 此时的maxq 是5435122，是偶数，那么我们首先判断这个2*2的面积是否满足
need2 = (maxq//2)**2
print(need2)
# need2 = 7385137788721 正好等于 a
# 所以结果就是 5435122

打表巧妙找规律

召唤数学精灵

在这里插入图片描述

思路分析：由于数字很大，所以不太可能逐一暴力，又因为是求解数目的题目，所以可以考虑先输出1000范围获得更大一点范围的结果，查看是否有规律！



def cheng(i):
    ans = 1
    for i in range(1,i+1):
        ans*=i
    return ans

for i in range(1001):
    if ((1+i)*i//2 - cheng(i))%100 == 0:
        print(i,end=" ")
print()
# 结果是 1 3 24 175 199 200 224 375 399 400 424 575 599 600 624 775 799 800 824 975 999 1000
# 可以看到除了 1 和 3
# 每200个数会出现 以24,75,99,00 结尾的四个数
a = 2024041331404202
zheng = a // 200
yu = a % 200
print(zheng,yu)
# 10120206657021 2
# 结果
# 由于余数 yu 小于24，所以余数部分不会产生新的结果，我们只需用开始的1和3 加上后面的 4*zheng即可
ans = 2 + 4* zheng
print(ans)
# 结果就是 40480826628086

斐波那契与7

在这里插入图片描述

数字范围十分大，直接全部模拟不太可能，所以还是考虑在小范围之内打表，找规律

dp = [0]*10**3
dp[0] = dp[1] = 1
ans = []
for i in range(2,10**3):
    dp[i] = dp[i-1] + dp[i-2]
    if dp[i] % 10 == 7:
        ans.append((i,dp[i]))
print(ans)
# 后面经过统计发现，每60数就会有8个以7结尾的项
# 由于202202011200刚好整除60，所以答案就是 
print(202202011200//60*8)

进制转换

穿越时空之门

在这里插入图片描述

思路分析：直接写代码，只要将对应的十进制转化为二进制和四进制表示即可


# 1-2024 ,二进制表示的数位之和等于四进制表示的位数之和

# 现在的问题回到，如何计算一个十进制的二进制与四进制

def gettwo(i):
    ans = []
    while i // 2 != 0:
        ans.append(i%2)
        i //= 2
    ans.append(i)
    return sum(ans)

def getfour(i):
    ans = []
    while i // 4 != 0:
        ans.append(i%4)
        i //= 4
    ans.append(i)
    return sum(ans)
count = 0
for i in range(1,2025):
    if gettwo(i) == getfour(i):
        count += 1
print(count)
# 答案是 63

取模问题

灵神相关知识点

数字串个数

在这里插入图片描述

思路分析：直接求解的话，肯定会超时，对此，我们可以采用差集的思想，我们直接用全集-不包含3-不包含7+同时不包含3和7

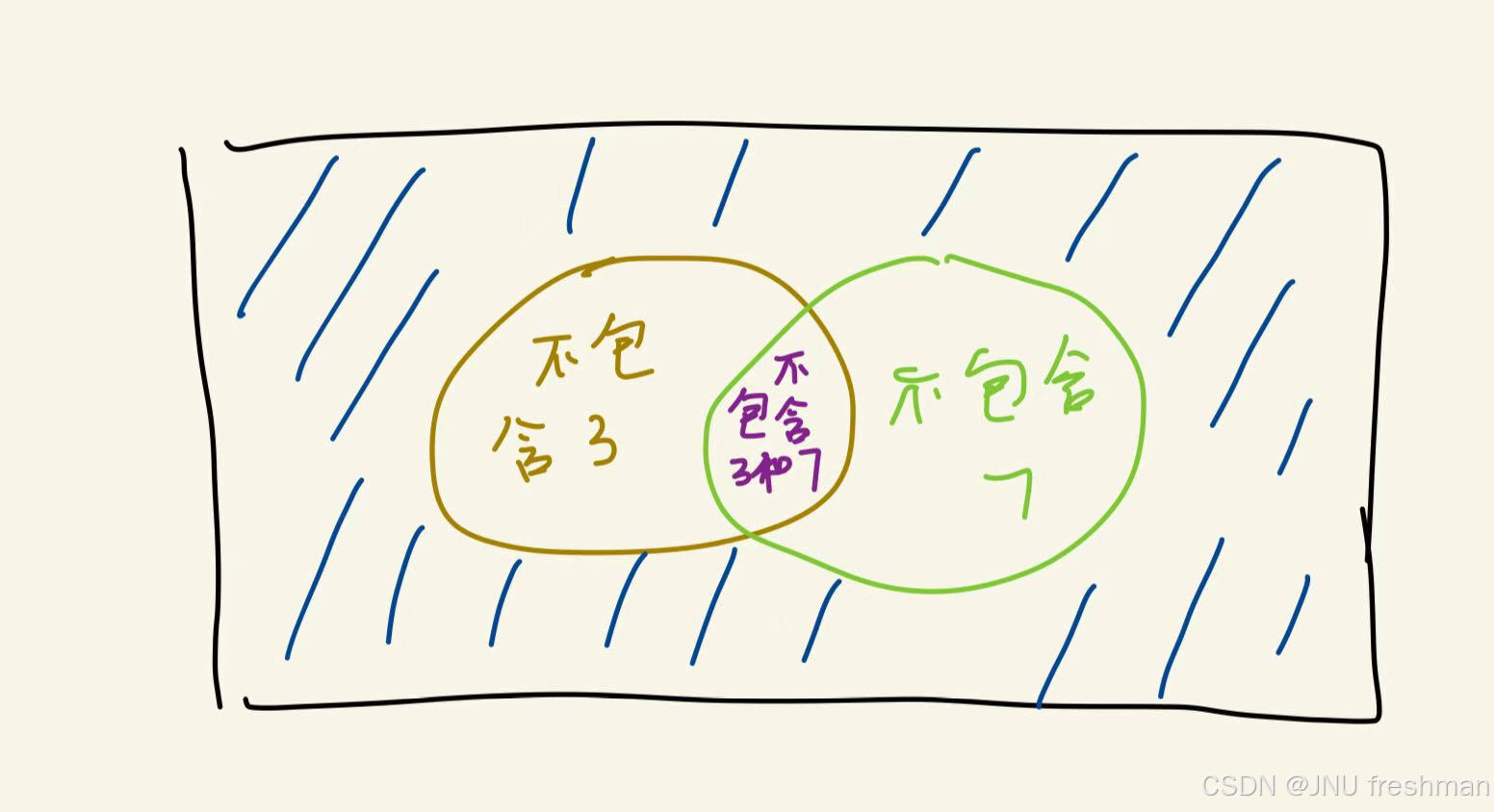
在这里插入图片描述

# 占位置的问题
# 总的来说，结果会很大
# 反着来做
# 先求解全部的情况-不包含7-不包含3+不包含7和不包含3

mod = 10**9+7
# 先求 9 ** 10000

ans1 = 1
for i in range(1,10001):
    ans1 = ans1*9%mod

# 求解不包含7的数字
ans2  = 1
for i in range(1,10001):
    ans2 = ans2*8%mod

ans2 = ans2 * 2 %mod

ans3 = 1
for i in range(1,10001):
    ans3 = ans3*7%mod

res = ans1 - ans2 + ans3
# (a+b-c）% d = (a%d + b%d - c%d)%d
print(res%mod)
# 结果是 157509472